Привет Лёва Середнячок
Составьте блок-схему алгоритма поиска корней квадратного уравнения ax2+bx+c=0
0 (0 оценок)
tisivlad 8 лет назад
Светило науки — 16 ответов — 232 помощи
PROGRAM KORNI;
uses crt;
var a,b,c,D:integer;
X1,X2 :real;
begin
Writeln (‘Введите a,b и c’);
read (a);
read (b);
read (c);
begin
D:= sqrt (b)-4*a*c;
If D end;
X1:=-b+SQRT(D)/(2*a);
X2:=-b-SQRT(D)/(2*a);
Writeln(‘D=’, D);
Writeln(‘X1=’,X1:4:2);
Writeln(‘X2=’,X2:4:2);
end.
Лучшие помощники
За сегодня
Ежедневный Еженедельный Ежемесячный За 3 месяца
Мозг Отвечающий
Лёва Середнячок
Мозг Отвечающий
Лёва Середнячок
Мозг Отвечающий
Лёва Середнячок
Мозг Отвечающий
Лёва Середнячок
2023 ВашУрок
Этот сайт использует cookies. Политика Cookies Вы можете указать условия хранения и доступ к cookies в своем браузере.
решаем квадратные уравнения в Excel
Установи приложение ВашУрок
Источник: vashurok.com
Русские Блоги
Java, чтобы найти квадратное уравнение с одной переменной: корень из ax2 + bx + c = 0
Найдите квадратное уравнение для одной переменной: корень из ax2 + bx + c = 0, a, b, c вводятся с клавиатуры
- Найдите одномерное квадратное уравнение: ax2 + bx + c = 0 root, a, b, c вводятся с клавиатуры.
- блок-схема:
- код:
- Рисунок результата работы программы:
Найдите одномерное квадратное уравнение: ax2 + bx + c = 0 root, a, b, c вводятся с клавиатуры.
блок-схема:
код:
package com.Squ.www; // Создаем пакет Squ import java.util.Scanner;// Импортируем класс Scanner в пакет java.util(Используйте этот класс, чтобы легко завершить операцию ввода входного потока) import java.math.BigDecimal;// Импортируем BigDecimal в пакет java.math(Используется для точных вычислений чисел с более чем 16 значащими цифрами) // Обсудить различные ситуации каждого коэффициента в квадратном уравнении одной переменной, перечислить распределение корней в разных ситуациях и, наконец, найти существующие корни public class Squ // Определяем публичный класс — Squ public static void main(String[]args) double X1,X2;// Определяем два решения System.out.println(«Выражение уравнения: ax ^ 2 ＋ bx ＋ c = 0»);// Отображение вывода консоли — Выражение уравнения: ax2 ＋ bx ＋ c = 0 Scanner sc=new Scanner(System.in);// Используйте класс Scanner для получения ввода с консоли(Получите номер, введенный с клавиатуры) System.out.println(«Пожалуйста, введите значение a:»);// Отображение подсказки вывода — ввод значения // Каждый раз, когда вы вводите значение с клавиатуры, нажимайте Enter, чтобы выполнить следующее содержимое double a=sc.nextDouble();// Принимаем число, введенное консолью, чтобы присвоить значение формальному параметру a System.out.println(«Пожалуйста, введите значение b:»);// Отображение подсказки вывода — ввод значения b double b=sc.nextDouble();// Принимаем число, введенное консолью, чтобы присвоить значение формальному параметру b System.out.println(«Пожалуйста, введите значение c:»);// Отображение подсказки вывода — ввод значения c double c=sc.nextDouble();// Принимаем число, введенное консолью, чтобы присвоить значение формальному параметру c double t=b*b-4*a*c;// Определяем переменную t и t=b * b-4 * a * c, в это время t — дискриминант корня уравнения // Используйте предложения для обсуждения различных условий коэффициентов уравнения и получения распределения корней // ① Определить, когда a, b и c равны 0, уравнение становится уравнением 0=0;Уравнения не существует! if(a==0 b==0 c==0) System.out.println(«Уравнения не существует!»);// Отображение вывода > // ② Когда и a, и b равны 0, а c не равно 0, уравнение превращается в уравнение c=0, неизвестных нет, уравнения не существует! else if(a==0 b==0 c!=0) System.out.println(«Уравнения не существует!»);// Отображение вывода > // ③ Когда a равно 0, а b и c не равны 0, уравнение превращается в одномерное линейное уравнение bx + c=0, в это время уравнение имеет только одно решение else if(a==0 b!=0 c!=0) System.out.println(«Это уравнение представляет собой линейное уравнение одной переменной»);// Отображение вывода double x1 = (-1 * c) / b;// Определяем переменный результат для хранения решения уравнения;Решение на данный момент: -c / b System.out.println(«Решение уравнения:» + resetValue(x1)); > // ④ Вышеуказанное определяет t=b * b-4 * a * c, если t>0, то корень t является действительным числом, а уравнение имеет два разных действительных корня, и два действительных корня являются противоположными числами. else if(t>0) System.out.println(«У уравнения два действительных корня»);// Отображение вывода // Алгоритм первого корня:((-b) + Math.sqrt(t)) / 2 * a( Math.sqrt относится к классу sqrt в математическом методе, а именно к квадрату) X1= ((-b) + Math.sqrt(t)) / 2 * a; // Алгоритм первого корня:((-b) — Math.sqrt(t)) / 2 * a X2= ((-b) — Math.sqrt(t)) / 2 * a; // Отображаем значение двух выходных System.out.println(«X1=»+resetValue(X1)); System.out.println(«X2=»+resetValue(X2)); > // ⑤ Если t0, то мнимое число генерируется после возведения t в квадрат, и уравнение имеет пару сопряженных вспомогательных корней else if(t0) // ⑥ Если b не равно 0, его корень является сопряженным вспомогательным корнем, а корень состоит из мнимой части и действительной части if(b!=0) X1=(-1*b)/(2*a);// Реальная часть корня X2=Math.sqrt(-1*t)/(2*a);// Мнимая часть корня System.out.println(«Уравнение имеет пару сопряженных комплексных корней:»);// Отображение вывода // ToString при выводе()Указывает, что значение корня выводится в экспоненциальной нотации.;Добавьте i, чтобы указать мнимую часть;один из них»+、-«Соедините действительную и мнимую части корня, чтобы образовать сопряженную System.out.println(«X1=»+resetValue(X1).toString()+»+» +resetValue(X2).toString()+»i»);// Выводим значение первого корня System.out.println(«X2=»+resetValue(X1).toString() + «-» + resetValue(X2).toString() + «i»);// Выводим значение второго корня > // ⑦ Если b=0, то корень имеет только мнимую часть и в это время нет действительной части, это пара сопряженных комплексных корней, действительная часть равна 0 else X1=Math.sqrt(-1*t)/(2*a);// Только мнимая часть в корне System.out.println(«У уравнения есть пара противоположных мнимых корней:»);// Отображение вывода // ToString при выводе()Указывает, что значение корня выводится в экспоненциальной нотации.;Добавьте i, чтобы указать мнимую часть;один из них»+、-«Соедините действительную часть и мнимую часть корня, чтобы образовать сопряженную, в это время действительная часть равна 0 System.out.println(«X1=0-«+resetValue(X1).toString()+»i»); System.out.println(«X2=0+»+resetValue(X1).toString()+»i»); > > // ⑧ Если t=0 уравнение имеет действительный корень else if(t==0) X1=(-1*b)/2*a;// Расчет корня System.out.println(«У уравнения есть настоящий корень»);// Отображение вывода System.out.println(«Решение уравнения:»+resetValue(X1));// Отображаем решение выходного уравнения > > // Используем статический метод для преобразования определенного значения из типа double в тип BigDecimal(заявление) private static BigDecimal resetValue(double n) // TODO автоматически генерирует заглушку метода BigDecimal bd=new BigDecimal(n);// Присваиваем значение n формальному параметру bd // Возвращаемое значение сохраняет два десятичных разряда, и используется метод округления по умолчанию (ROUND_HALF_UP означает ввод 1 при достижении 5; setScale указывает количество сохраняемых десятичных знаков) return bd.setScale(2,BigDecimal.ROUND_HALF_UP); > >
Источник: russianblogs.com
НАХОДИМ КОРНИ КВАДРАТНОГО УРАВНЕНИЯ С ПОМОЩЬЮ PYTHON — If/Else **Программа решает за тебя!**
Вычислить корни квадратного уравнения блок схема
Запустите программу на выполнение и решите следующие квадратные уравнения:
а) 1125 х 2 — 45 х — 324 = 0
б) 502 х 2 — 38,5 х + 12,125 = 0
в) 16 х 2 — 256 х + 1024 = 0
Задача 2. Составить блок-схему и программу, определяющие количество корней квадратного уравнения
ПРОГРАММА на БЕЙСИК
PRINT “Количество корней квадратного уравнения“
INPUT “Ввести a, b, c: “, a, b, c
d = b * b – 4 * a * c
IF d > 0 THEN PRINT “2 разных корня“ ELSE PRINT “2 одинаковых корня“
ELSE PRINT “Действительных корней нет“
Запустите программу на выполнение и определите количество корней в следующих квадратных уравнениях:
а) 1125 х 2 — 45 х — 324 = 0
б) 502 х 2 — 38,5 х + 12,125 = 0
в) 16 х 2 — 256 х + 1024 = 0
Задача 3*. Составить блок-схему и программу, определяющие имеет ли квадратное уравнение ax 2 + bx + c = 0 хотя бы один корень, больший числа m .
Запустите программу на выполнение и определите имеется ли корень в следующих квадратных уравнениях:
а) 1125 х 2 — 45 х — 324 = 0 при m = 0
б) 502 х 2 — 38,5 х + 12,125 = 0 при m = 15
в) 16 х 2 — 256 х + 1024 = 0 при m = 7
Домашнее задание — Составить блок-схемы и программы для следующих задач:
Задача 1. Определить является ли введенное с клавиатуры число корнем квадратного уравнения ax 2 + bx + c = 0 .
Разберем следующий пример составления схемы алгоритма и с помощью графических средств MS Word изобразим его.
Действительные корни квадратного уравнения ax 2 + bx + c = 0, заданного коэффициентами a, b, c, вычисляются следующим образом (при условии, что а 0):
1. Прочитать коэффициенты a, b, c.
2. Вычислить дискриминант d = b 2 – 4ac.
3. Если d>0, вычислить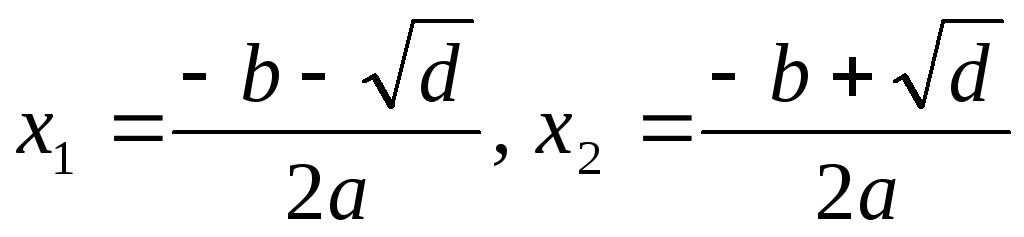 
и написать эти числа, иначе, если d = 0, вычислить 
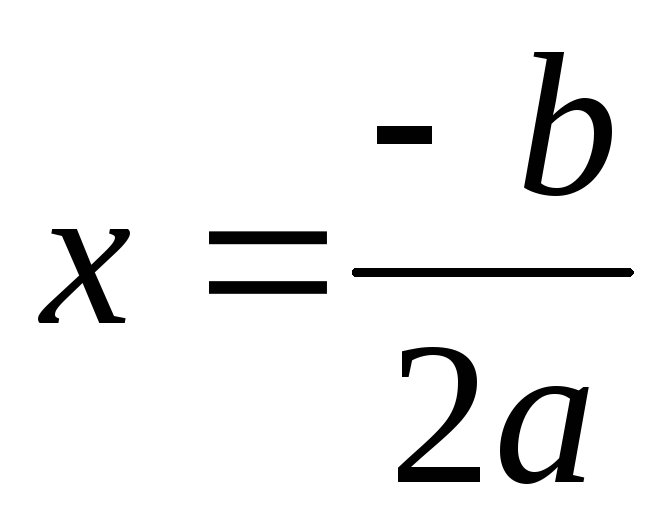и написать это число, иначе написать «действительных корней нет».
По алгоритму выполняется соответствующая последовательность действий, или процесс решения задачи:
Прочитать коэффициенты, вычислить d, проверить, что d > 0 (и это так), вычислить х1, х2 и написать эти числа.
Прочитать коэффициенты, вычислить d, проверить, что d > 0 (и это не так), проверить, что d = 0 (и это так), вычислить х и написать это число.
Прочитать коэффициенты, вычислить d, проверить, что d > 0 (и это не так), проверить, что d = 0 (и это не так), и написать, что действительных корней нет.
Схема алгоритма, выполненного с помощью графических средств MS Word, приведена на рис. 6.
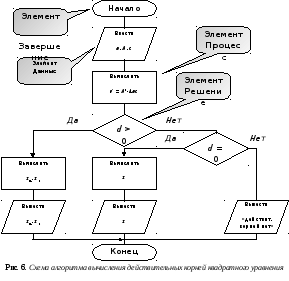
В данной схеме используются следующие графические примитивы:
Знак завершения – обозначает начало и конец алгоритма.
Данные – обозначает ввод и вывод данных.
Процесс – обозначает вычислительные операции.
Решение – обозначает выбор одной из альтернатив.
2. Изображение схем алгоритмов с помощью программы Microsoft Visio
Microsoft Visio – программный продукт, предназначенный для создания технических и деловых диаграмм. К его возможностям относятся следующие:
визуальное отображение процессов, концепций и отношений;
легкость формирования диаграмм, путем перетаскивания (метод drag
генерация схем различных типов на основе существующих данных;
наличие системы контекстных подсказок и справочной информации;
импорт и экспорт диаграмм, в формате Scalable Vector Graphics (SVG) (основан на технологии XML);
интеграция бизнес-процессов и систем путем извлечения данных из диаграмм Visio и импорта этой информации в форматы Microsoft Excel, Word, Access, Microsoft SQL Server, XML и др.
Запуск программы и ее интерфейс
Для запуска программы выполните команды Главного меню:Пуск Программы Microsoft Office Microsoft Office Visio или выполните двойной щелчок на ярлыке этой программы, расположенном на Рабочем столе.
Откроется окно программы, в котором предлагается выбрать Шаблон (набор графических примитивов). Для построения схем алгоритмов в списке Разделы выберите Flowchart, а в списке Шаблоны выполните двойной щелчок мышью по значку Basic Flowchart (рис. 7).
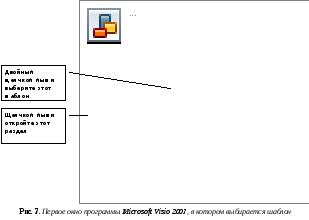
После этого откроется главное окно программы (рис. 8), имеющее стандартный для MS Office вид. Основную часть интерфейса занимают два окна: Шаблоны (Stencils) – слева, с зеленым фоном) и Рисунок (Drawing).
Блок-схемой называется наглядное графическое изображение алгоритма. В блок-схеме отдельные этапы алгоритма изображают при помощи различных геометрических фигур – блоков. Последовательность выполнения этапов указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями. Типичные действия алгоритма изображаются геометрическими фигурами представленными в табл. 7.
Таблица 7. Изображение основных действий алгоритма.
| Название блока | Изображение блока | Надпись на блоке |
| Начало (конец) алгоритма | «начало» («конец») | |
| Ввод – вывод данных | «ввод» («вывод») и список переменных. | |
| Решение (арифметический) | операция или группа операций | |
| Условный блок | логическое условие |
Составной оператор
Это группа операторов, отделенных друг от друга точкой с запятой, начинающихся с открывающей фигурной скобки .
Транслятор воспринимает составной оператор как один оператор.
Операторы ветвления
Алгоритмы разветвленной структуры (рис. 4) применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие.
Рис. 4. Блок-схема алгоритма разветвляющейся структуры
Условный оператор, соответствующий приведенной блок-схеме, имеет вид:
if (выражение) оператор_1;
Вычисляется выражение. Если оно не равно нулю, т.е. имеет значение true, выполняется оператор_1, в противном случае (выражение равно нулю, т.е. false) – оператор_2.
Если в зависимости от некоторого условия выполняется некоторое действие, а в противном случае ничего не происходит, то алгоритм имет вид (рис. 5):
Рис. 5. Блок-схема алгоритма разветвляющейся структуры, без альтернативного действия
Условный оператор в этом случаеимет конструкцию:
if (выражение) оператор;
Эту запись можно назвать «пропуск оператора else». Здесь оператор либо выполняется, либо пропускается, в зависимости от значения выражения.
Если в какой-либо ветви условного процесса требуется выполнить несколько операторов, следует использовать составной оператор.
Распространенные ошибкипри программировании условных процессов:
1. Неверное использование операций проверки равенства (==) и присваивания (=). Например,
if (a=1) b=0; //НЕ ВЕРНО[4]
2. Запись проверки на принадлежность диапазону. Например,
if if (0 2 +bx+c=0. Вычислить корни квадратного уравнения.
Входные данные: a, b, c.
Алгоритм решения задачи в виде блок-схемы представлен на рис. 6.
Рис. 6. Алгоритм решения квадратного уравнения
Если выражение=значение_1, то выполняются операторы_1.Если выражение =значение_2, то выполняются операторы_2 и т .д.
Если выражение не принимает ни одно из имеющихся значений из списка, то выполняются операторы, указанные после оператора default. Ветвь default может отсутствовать.
ЗАДАЧА 6.Вывести на печать название дня недели, соответствующее заданному числу D, при условии, что в месяце 31 день и 1-е число – понедельник.
Если остаток от деления заданного числа D на семь равен единице, то это понедельник, двойке – вторник, тройке – среда и так далее. Выражение D % 7 может принимать только одно из значений: 1, 2, 3, 4, 5, 6 или 0. В записи оператора варианта ветвь default будет отсутствовать.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 — | 7304 — или читать все.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Нет связанных сообщений
Источник: mnogotolka.ru