Функция для нахождения минимального расстояния от точки до отрезка по координатам.
PHP-функция
Аргументы функции:
$x , $y — координаты точки C.
$x1 , $y1 , $x2 , $y2 — координаты двух точек, они описывают отрезок AB.
function distancePointToLine($x, $y, $x1, $y1, $x2, $y2) < $A = $x — $x1; $B = $y — $y1; $C = $x2 — $x1; $D = $y2 — $y1; $dot = $A * $C + $B * $D; $len_sq = $C * $C + $D * $D; $param = -1; if ($len_sq != 0) < $param = $dot / $len_sq; >$xx = $yy = 0; if ($param < 0) < $xx = $x1; $yy = $y1; >else if ($param > 1) < $xx = $x2; $yy = $y2; >else < $xx = $x1 + $param * $C; $yy = $y1 + $param * $D; >$dx = $x — $xx; $dy = $y — $yy; return array(‘x’ => $xx, ‘y’ => $yy, ‘d’ => sqrt($dx * $dx + $dy * $dy)); >
В результате получится массив:
x , y – координаты пересечения на отрезке AB.
d – расстояние от точки С до отрезка.
JS-функция
function distancePointToLine(x, y, x1, y1, x2, y2) < A = x — x1; B = y — y1; C = x2 — x1; D = y2 — y1; dot = A * C + B * D; len_sq = C * C + D * D; param = -1; if (len_sq != 0) < param = dot / len_sq; >xx = yy = 0; if (param < 0) < xx = x1; yy = y1; >else if (param > 1) < xx = x2; yy = y2; >else < xx = x1 + param * C; yy = y1 + param * D; >dx = x — xx; dy = y — yy; return ; >
Источник: snipp.ru
Определить расстояние от точки С до прямой АВ. Метод прямоугольного треугольника.
Расстояние от точки до отрезка программа
Nickolay.info. Алгоритмы. Расстояние от точки до отрезка
При работе с графикой часто нужно определить расстояние от заданной точки с координатами (Х0, Y0) до отрезка прямой, проходящей через две точки с координатами (Х1, Y1) и (X2, Y2) . При этом мы должны рассмотреть уравнение прямой, проходящей через две точки, заданные координатами (Х1, Y1) и (X2, Y2) , в общем виде:
А*х+В*у+С = 0
Кратчайшее расстояние от точки, заданной координатами (Х0,Y0) , до прямой, заданной уравнением А*х+В*у+С=0 , может быть определено с использованием уравнения:
A*x/T + B*y/T + C/T = 0
в котором Т=корень(А 2 +В 2 ) , причём С (что достигается изменением знака выражения). При подстановке в уравнение координат произвольной точки получаем значение кратчайшего расстояния от рассматриваемой точки до прямой.
При определении расстояния от точки до отрезка нужно сначала проанализировать взаимное расположение точки и отрезка прямой, то есть, проверить, куда опустится перпендикуляр из точки (Х0, Y0) : непосредственно на отрезок или на прямую, являющуюся продолжением рассматриваемого отрезка. Этот анализ может быть произведен путем построения треугольника, вершинами которого являются заданные точки (Х0, Y0) , (Х1, Y1) , (Х2, Y2) , и сопоставления соотношения длин его сторон R1 , R2 , R12 . Вариант программы представлен ниже, выводы о том, что точка находится «левее» или «правее» отрезка условны, они имеют смысл, только если задаётся X12 .
Расстояние от точки до прямой (метод координат)
var x,y:array [0..2] of real; r0,r1,r2,r12,a,b,c,t:real; i:integer; function dist (x1,y1,x2,y2:real):real; begin dist:=sqrt(sqr(x2-x1)+sqr(y2-y1)); end; begin writeln; for i:=0 to 2 do begin repeat write (‘Введите R’,i,’ (координаты X и Y):’); readln (x[i],y[i]); until IoResult=0; end; r1:=dist(x[0],y[0],x[1],y[1]); r2:=dist(x[0],y[0],x[2],y[2]); r12:=dist(x[1],y[1],x[2],y[2]); if r1>=dist(r2,r12,0,0) then writeln (‘Точка правее (x2,y2),r=’,r2:6:2) else if r2>=dist(r1,r12,0,0) then writeln (‘Точка левее (x1,y1),r=’,r1:6:2) else begin a:=y[2]-y[1]; b:=x[1]-x[2]; c:=-x[1]*(y[2]-y[1])+y[1]*(x[2]-x[1]); t:=dist (a,b,0,0); if c>0 then begin a:=-a; b:=-b; c:=-c; end; r0:=(a*x[0]+b*y[0]+c)/t; write (‘Расстояние от точки до отрезка=’,r0:6:2); if r0
Источник: nickolay.info
Расстояние от точки до отрезка
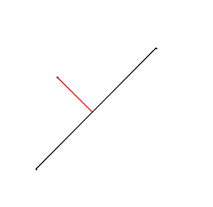
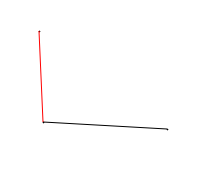
Расстоянием от точки до отрезка является либо перпендикуляр, опущенный из этой точки на отрезок, либо минимальное расстояние от точки до одного из концов отрезка.
Если треугольник, вершинами которого является данная точка и концы заданного отрезка, является тупоугольным (проверка на тупоугольность проводится рассмотрением знака скалярного произведения соответствующих векторов, построенных на сторонах треугольника (кос тупого угла отрицательный))(т. е. из данной точки невозможно опустить перпендикуляр на данный отрезок), то расстоянием от точки до отрезка считается минимальное расстояние от данной точки, до одного из концов отрезка. Оно определяется с помощью формулы:
((х1- х2) 2 + (у1 — у2) 2 ) -1/2 .
Если все же перпендикуляр опустить возможно, то расстоянием от точки до отрезка считается длина этого перпендикуляра. Ее можно определить двумя способами:
1) посчитав площадь треугольника по двум формулам (полувысота на сторону и полупроизведение сторон на синус угла между ними) мы можем выразить высоту как:
h = (AC • AB • sin (AC, AB)) / BC ;
2) можем определить координаты точки пресечения отрезка с перепендикуляром, опущенным из данной точки на отрезок и посчитать расстояние между двумя точками. Для этого сначала нам надо найти уравнение перпендикуляра к данной прямой, проходящего через данную точку, затем решить систему уравнений (k и l — координаты вершины перпендикуляра, x1, y1, x2, y2 — координаты концов отрезка):
(1)(x — x1)(y2 — y1) = (y — y1)(x2 — x1)
(2) (x — k)(x2 — x1) = — (y — l)(y2 — y1)
Если (x2 — x1) = 0, то решение:
x = x1
y = l.
Если (y2 — y1) = 0, то решение:
y = y1
x = k.
В остальных случаях (пусть (x2 — x1) = α, (y2 — y1) = β):
x = (α / β) (y — y1) + x1
y = ((α 2 / β)y1 + α (k — x1) + βl) / ((α 2 / β) + β).
Источник: grafika.me