Допустим у нас есть правила обмена данными. При этом два разных правила конвертации объектов используют абсолютно одинаковые по структуре выборки данных, только с разными параметрами. Возникает резонный вопрос, а можно ли где-нибудь зафиксировать этот запрос, а затем использовать его во всех местах где нужно. Для этих целей существуют Запросы.
Технология использования очень проста. На закладке «Запросы» создаем и описываем текст запроса:
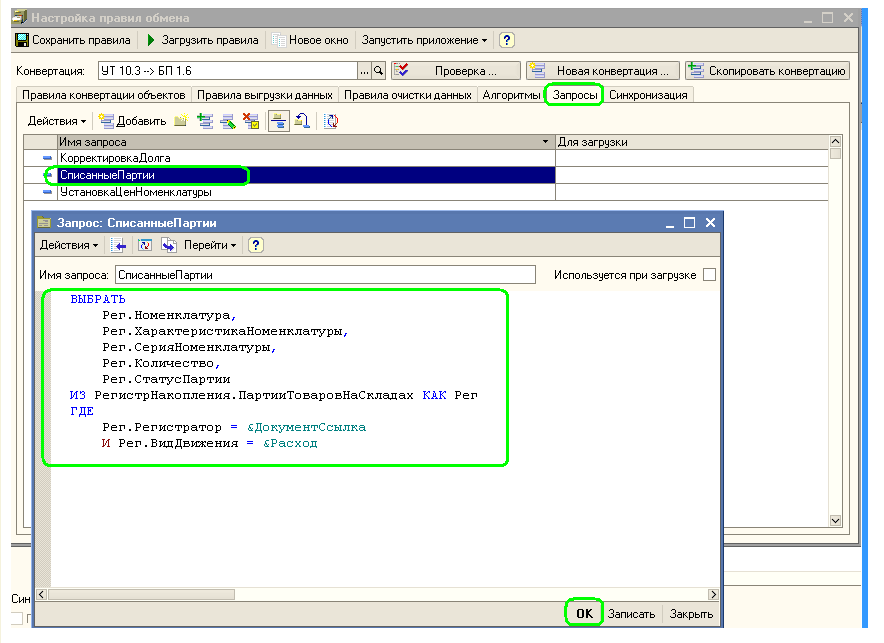
Далее в тексте обработчиков можно использовать такой код:
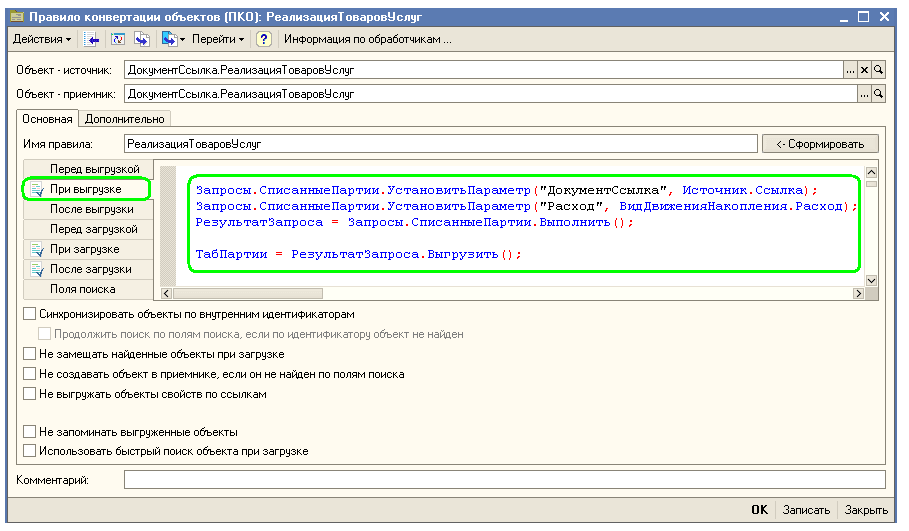
Аналогично обстоят дела с алгоритмами. Кода один и тот же кусок кода должен быть выполнен в различных местах, удобно записать отдельный алгоритм, а затем просто вызывать его из тех мест, где он нужен.
Гайд по программе «Алгоритм 2» #1 [Основы]

А вызов этого кода будет очень прост:
Выполнить(Алгоритмы.СоздатьТаблицу);
С уважением, Владимир Милькин (преподаватель школы 1С программистов и разработчик обновлятора).

Как помочь сайту: расскажите (кнопки поделиться ниже) о нём своим друзьям и коллегам. Сделайте это один раз и вы внесете существенный вклад в развитие сайта. На сайте нет рекламы, но чем больше людей им пользуются, тем больше сил у меня для его поддержки.
Нажмите одну из кнопок, чтобы поделиться:
Источник: helpme1s.ru
§ 2.3. Конструирование алгоритмов

Существуют различные методы конструирования (разработки, построения) алгоритмов. Мы познакомимся с одним из них — методом последовательного построения (уточнения) алгоритма. Иначе он называется методом разработки «сверху вниз», нисходящим методом или методом пошаговой детализации.
Процесс последовательного построения алгоритма выглядит следующим образом.
На первом шаге мы считаем, что перед нами совершенный исполнитель, который «всё знает и всё умеет». Поэтому достаточно определить исходные данные и результаты алгоритма, а сам алгоритм представить в виде единого предписания — постановки задачи (рис. 2.2).
Алгоритм #1 Создание простой программы, в Алгоритм 2.7

Если исполнитель не обучен исполнять заданное предписание, то необходимо представить это предписание в виде совокупности более простых предписании (команд). Для этого:
- задачу разбивают на несколько частей, каждая из которых проще всей задачи;
- решение каждой части задачи формулируют в отдельной команде, которая также может выходить за рамки системы команд исполнителя;
- при наличии в алгоритме предписаний, выходящих за пределы возможностей исполнителя, такие предписания вновь представляются в виде совокупности ещё более простых предписаний.
Процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.
Объединяя полученные предписания в единую совокупность выполняемых в определённой последовательности команд, получаем требуемый алгоритм решения исходной задачи.
Разработка алгоритма методом последовательного уточнения для исполнителя Робот
Вы уже знакомы с исполнителем Робот. Он действует на клетчатом поле, между клетками которого могут быть стены.
Система команд исполнителя Робот:


В одном условии можно использовать несколько команд, применяя логические операций И, ИЛИ, НЕ.
Известно, что Робот находится где-то в горизонтальном коридоре. Ни одна из клеток коридора не закрашена.

Составим алгоритм, под управлением которого Робот закрасит все клетки этого коридора и вернётся в исходное положение.

Представим план действий Робота следующими укрупнёнными шагами (модулями):

Детализируем каждый из пяти модулей.
1. Чтобы закрасить все клетки коридора, находящиеся левее Робота, прикажем Роботу шагнуть влево и выполнить цикл-ПОКА:
Под управлением этого алгоритма Робот закрасит все клетки коридора, находящиеся левее от него, и окажется на клетке рядом с левой границей коридора.

2. Командой вправо вернём Робота в коридор. Наша задача — вернуть Робота в исходную точку. Эта точка имеет единственный отличительный признак — она не закрашена. Поэтому пока занимаемая Роботом клетка оказывается закрашенной, будем перемещать его вправо.
Под управлением этого алгоритма Робот окажется в исходной клетке.

4. Так как, выполнив предыдущий алгоритм, Робот оказался правее коридора, командой влево вернём его в коридор. Возвращение в исходную точку обеспечивается алгоритмом:

- влево
- нц пока клетка закрашена
- влево
- кц
5. По команде закрасить Робот закрашивает исходную клетку.
Полностью программа управления Роботом выглядит так:
Вспомогательные алгоритмы
При построении новых алгоритмов нередко возникают ситуации, когда в разных местах алгоритма необходимо выполдение одной и той же последовательности шагов обработки данных. Для такой последовательности шагов создают отдельный алгоритм, называемый вспомогательным. В качестве вспомогательных могут использоваться алгоритмы, ранее разработанные для решения других задач.
Вспомогательный алгоритм — алгоритм, целиком используемый в составе другого алгоритма.
Пример 1. В среде КуМир составим алгоритм для исполнителя Робот, под управлением которого он нарисует узор:

Начальное положение Робота отмечено звёздочкой. В алгоритме использован вспомогательный алгоритм фигура.
При представлении алгоритмов с помощью блок-схем для обозначения команды вызова вспомогательного алгоритма используется блок «предопределённый процесс» (рис. 2.3), внутри которого записывается название (имя) вспомогательного алгоритма, после которого в скобках перечисляются параметры — входные данные и результаты.

Вспомогательный алгоритм делает структуру алгоритма более понятной.
Пример 2.
Вспомним алгоритм вычисления степени с натуральным показателем у = а n . Соответствующая блок-схема:

Степень с целым показателем у = а х , где х — целое число, а ? 0 вычисляется так:

В приведённой записи дважды фигурирует вычисление степени с натуральным показателем. Поэтому в алгоритм вычисления степени с целым показателем можно включить вызов вспомогательного алгоритма вычисления степени с натуральным показателем. Соответствующая блок-схема:

Алгоритм, представленный на блок-схеме, является основным по отношению к вызываемому в нём вспомогательному алгоритму.
Параметрами используемого вспомогательного алгоритма являются величины а, n, у. Это формальные параметры, они используются при описании алгоритма. При конкретном обращении к вспомогательному алгоритму формальные параметры заменяются фактическими параметрами, т. е. именно теми величинами, для которых будет исполнен вспомогательный алгоритм. Типы, количество и порядок следования формальных и фактических параметров должны совпадать.
Команда вызова вспомогательного алгоритма исполняется следующим образом (рис. 2.4):

- 1) формальные входные данные вспомогательного алгоритма заменяются значениями фактических входных данных, указанных в команде вызова вспомогательного алгоритма;
- 2) для заданных входных данных исполняются команды вспомогательного алгоритма;
- 3) полученные результаты присваиваются переменным с именами фактических результатов;
- 4) осуществляется переход к следующей команде основного алгоритма.
Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.
Рассмотрим несколько примеров рекурсивных алгоритмов.
Пример 3. Алгоритм вычисления степени с натуральным показателем n для любого вещественного числа а можно представить в виде рекурсивного:

n-я степень числа а есть не что иное, как произведение а n-1 • а; в свою очередь, а n-1 = а n-2 • а и т. д.
Пример 4. Рекурсивный алгоритм положен в основу эффективно го решения головоломки «Ханойская башня».

- Интерактивная игра «Ханойские башни» (195747) поможет вам вспомнить условие и алгоритм решения головоломки (http://sc.edu.ru/).
Пример 5. Рассмотрим алгоритм построения геометрической фигуры, которая называется снежинкой Коха. Шаг процедуры построения состоит в замене средней трети каждого из имеющихся отрезков двумя новыми такой же длины, как показано на рисунке:

С каждым шагом фигура становится всё причудливее. Граница снежинки Коха — положение кривой после выполнения бесконечного числа шагов.
Попробуйте подсчитать, сколько рёбер в границе снежинки Коха после четвёртого шага; после пятого шага.
САМОЕ ГЛАВНОЕ
Один из основных методов конструирования алгоритмов — метод последовательного построения алгоритма. Его суть состоит в том, что: исходная задача разбивается на несколько частей, каждая из которых проще всей задачи, и решение каждой части формулируется в отдельной команде; если получаются команды, выходящие за пределы возможностей исполнителя, то они представляются в виде совокупности ещё более простых предписаний. Процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.Вспомогательный алгоритм — алгоритм, целиком используемый в составе другого алгоритма.Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Дополняет ли презентация информацию, содержащуюся в тексте параграфа?
Источник: murnik.ru