Внеурочное занятие по математике в 4 классе. Тема: Решение текстовых задач
Цель: научить решать текстовые задачи различных видов, составлять краткую запись условия задачи, выделять ключевые слова в тексте; потренироваться в умении составлять математическую модель текстовых задач, сочинять эстетически красивые тексты задач по известному выражению, представляющему решение задачи.
Ход занятия
Решение задач.
Задача 1. С двух ульев получено 100 кг меда, причем с одного из них — на 4 кг больше, чем с другого.
Сколько меда получено с каждого улья?
1) 100 — 4 = 96 (кг)
Ответ: 48 кг и 52 кг.
Задача 2. Заяц пробегает 14 км за 2 часа, а сокол за 3 ч пролетает 210 км. Во сколько раз сокол движется быстрее зайца? На сколько км/ч скорость зайца меньше скорости сокола?
1) 14 : 2 = 7 (км/ч) — скорость зайца;
2) 210 : 3 = 70 (км/ч) — скорость сокола;
3) 70 : 7 = 10 (раз) — во столько раз быстрее.
4) 70 — 7 = 63 (км/ч) — на столько меньше.
Методика решения текстовых задач — bezbotvy
Ответ: сокол движется быстрее зайца в 10 раз; скорость зайца меньше скорости сокола на 63 км/ч.
Задача 3. Туристы прошли 14 км и сделали привал. После привала они прошли на 6 км меньше, чем до привала, и остановились на ночлег. Им предстояло пройти еще в 3 раза больше, чем они прошли. Какой длины путь был намечен?
1) 14 — 6 = 8 (км) — после привала;
2) 14 + 8 = 22 (км) — до ночлега;
3) 22 • 3 = 66 (км) — после ночлега;
4) 66 + 22 = 88 (км) — весь путь.
Задача 4. За день на фабрике изготовили 1240 м ситца, шерсти — в 4 раза меньше, чем ситца, вельвета — на 490 м больше, чем шерсти, а полотна столько, сколько шерсти и вельвета вместе. Сколько всего ткани изготовили на фабрике за этот день?
1) 1240 : 4 = 310 (м)- шерсть;
2) 310 + 490 = 800 (м) — вельвет;
3) 310 + 800 = 1110 (м) — полотно;
4) 1240 + 1110 + 1110 = 3460 (м) — всего.
Ответ: 3460 метров.
Задача 5. Геологи 3 ч летели на вертолете со скоростью 95 км/ч, затем 2 ч ехали верхом со скоростью 12 км/ч. Какой путь проделали геологи за это время?
1) 95 • 3 = 285 (км) — путь на вертолете;
2) 12 • 2 = 24 (км) — путь верхом;
3) 185 + 24 = 209 (км) — весь путь.
Задача 6. В роще 240 берез, а кленов — на 93 меньше. Сосен в ней вдвое больше, чем кленов, а елей — в 3 раза меньше, чем сосен и берез вместе. Сколько всего деревьев в этой роще?
1) 240 — 93 = 147 (д.) — кленов;
2) 147-2 = 294 (д.) — сосен;
3) 240 + 294 = 534 (д.) — сосен и берез;
4) 534:3 = 178 (д.) — елей;
5) 147 +534 + 178 = 859 (д.) — всего.
Ответ: 859 деревьев.
Задача 7. Из леса принесли 38 грибов: белых, подосиновиков и подберезовиков. Подберезовиков в 4 раза больше, чем белых, а подберезовиков и подосиновиков вместе 34 гриба.
Сколько грибов каждого вида принесли из леса?
1) 38 — 34 = 4 (г.) — белых;
2) 4 • 4 = 16 (г.) — подберезовиков;
3) 34 — 16 = 18 (г.) — подосиновиков.
Урок 11. Решение текстовых задач. Задачи на движение, задачи на работу. Вебинар | Математика
Ответ: 4 белых, 16 подберезовиков, 18 подосиновиков.
Домашнее задание:
Задача 1. В двух пачках 160 тетрадей, причем в одной из них на 20 тетрадей больше, чем в другой. Сколько тетрадей в каждой пачке?
1) 160 — 20 = 140 (т.) — было бы в 2 пачках, если бы было поровну;
2) 140 : 2 = 70 (т.) — в меньшей пачке;
3) 70 + 20 = 90 (т.) — в большей пачке.
Ответ: 70 и 90 тетрадей.
Задача 2. В двух пачках 160 тетрадей, причем в одной из них в 3 раза больше тетрадей, чем в другой. Сколько тетрадей в каждой пачке?
Пусть х — число тетрадей в одной пачке, тогда Зх — число тетрадей в другой пачке. Всего 160 тетрадей.
40 • 3 = 120 (т.) — во второй пачке.
Ответ: 40 и 120 тетрадей.
Задача 3. Библиотеке нужно переплести 1800 книг. Одна мастерская может выполнить эту работу за 3 дня, а другая — за 6 дней. За сколько дней переплетут все книги обе мастерские, если будут работать одновременно?
1) 1800 : 3 = 600 (кн.) — 1-я мастерская за 1 день;
2) 1800 : 6 = 300 (кн.) — 2-я мастерская за 1 день;
3) 600 + 300 = 900 (кн.) — две мастерские за 1 день;
4) 1800 : 900 = 2 (дн.).
Ответ: за 2 дня обе мастерские переплетут все книги.
Источник: ped-kopilka.ru
Элективный курс математики для 9 класса «Решение текстовых задач»
В связи с переходом на профильное обучение возникла необходимость в обеспечении углубленного изучения предмета и подготовки учащихся к продолжению образования.
Владение приемами решения задач можно считать критерием знаний основных разделов школьной математики, уровня математического, продуктивного и логического мышления.
Разработана и апробирована программа элективного курса. Систематизирован теоретический и дидактический материал. Результативность
Учащиеся более уверенно решают текстовые задачи.
В связи свыше сказанным, возникла необходимость в разработке и внедрении в учебный процесс элективного курса по математике по теме: «Решение текстовых задач».
Основными формами проведения элективного курса являются изложение узловых вопросов курса в виде обобщающих лекций, семинаров, дискуссий, практикумов по решению задач, рефератов учащихся.
1.Обобщение, углубление и систематизирование знаний по решению текстовых задач.
2.Определение уровня способности учащихся и их готовности в дальнейшем к профильному обучению в школе.
3.Развитие продуктивного мышления учащихся.
4.Развитие устойчивого интереса учащихся к изучению математики.
5.Воспитание понимания, что математика является инструментом познания окружающего мира.
1.Вооружить учащихся системой знаний по решению текстовых задач.
2.Сформировать умения и навыки при решении разнообразных задач различной сложности.
3.Способствовать формированию познавательного интереса к математике, развитию творческих способностей учащихся.
4.Повысить уровень математической подготовки учащихся.
5.Развивать и укреплять межпредметные связи.
6.Применять математические знания в решении проблемных задач.
7.Формировать независимость, гибкость и критичность мышления.
8.Развивать исследовательскую и проектную деятельность учащихся.
9.Обеспечить условия для самостоятельной творческой работы.
Конспект урока математики в 4 классе «Решение текстовых задач арифметическим и алгебраическим способами»
— Ребята, сегодня наш урок математики пройдет в необычном месте. (выносят предположения)
— Я приглашаю вас на заочную экскурсию в Сихотэ-Алинский государственный природный заповедник.
Два ученика читают информацию:
Сихотэ-Алинский государственный природный биосферный заповедник имени Константина Георгиевича Абрамова – самый северный и самый большой в Приморском крае. Сихотэ-Алинь – горная страна в России, в Приморском и Хабаровском краях, между Японским морем и долинами рек Уссури и Амур.
В переводе с китайского языка Сихотэ-Алинь означает – хребет больших западных рек. Это родина уссурийских (амурских) тигров, самых больших представителей семейства кошачьих. Заповедник внесен в Список Всемирного наследия ЮНЕСКО в 2001 году.
Сихотэ-Алинский государственный природный биосферный заповедник
Более100 фотоловушек идентифицируют краснокнижных тигров по индивидуальному узору полос. Специалисты знают рисунок каждого зверя.
По данным последней переписи, в заповеднике обитает около 20 хищников.
Один из самых удобных средств круглосуточного и всепогодного наблюдения за поведением тигров в естественной среде обитания – это использование радиоошейника. Надеть его на хищника не так просто. Чтобы поймать тигра, ученые используют специальные петли-капканы. Из специального оружия животных усыпляют на 20 минут и закрепляют радиоошейники.
Радиоошейники помогают ученым отслеживать маршруты тигров, их повадки, дают возможность прийти на помощь попавшему в беду тигру
Задача
Для учета популяции уссурийского тигра экологам заповедника «Сихотэ-алинский» необходимо надеть радиоошейники 14 тиграм. В первый месяц ошейников надели в 2 раза больше, чем во второй. А в третий месяц экологам удалось надеть 5 радиоошейников. Сколько тигров взяли под наблюдение экологи в первый месяц?
Алгоритм решения
— Что известно в задаче?
— Что надо найти?
— Какие способы решения вы знаете? (арифметический и алгебраический)
1 способ (арифметический)
Схема задачи:
1) 14–5= 9(т.) – в 1-ый и 2-ой месяц.
2) 2+1=3 (части) – в 1-ый и 2-ой месяц.
3) 9_3=3 (т.) – в 1 части или во 2-ом месяце.
4) 3∙2=6 (т.)
Ответ: 6 тигров взяли под наблюдение экологи в первый месяц.
2 способ (алгебраический)
1) Определим какую неизвестную величину обозначить переменной. Пусть х тигров – количество тигров, взятых под наблюдение во второй месяц.
2) Через эту переменную выразим остальные неизвестные величины в соответствии с условием задачи. Тогда 2х – количество тигров, взятых под наблюдение в первый месяц.
3) Исходя из условия задачи, составим уравнение, связывающее все неизвестные. По условию задачи в третий месяц экологам удалось надеть 5 радиоошейников, а всего надели радиоошейники 14 тиграм.
Получим уравнение: х+2х+5=14
4) Решим полученное уравнение:
3х+5=14
3х=14–5
3х=9
х=3 (т.) – во 2-ой месяц.
5) Ответим на вопрос задачи:
3∙2=6(т.) – взяли под наблюдение в 1-ом месяце.
Ответ: 6 тигров взяли под наблюдение экологи в первый месяц.
Итог урока
— Как решали задачу? (по действиям и уравнением)
— Какой раздел математики изучает решение задач по действиям? (арифметика – наука о числах и операциях над ними)
— Как будет называться этот способ решения? (арифметический)
— Как называется раздел математики изучающий уравнения? (алгебра – наука, которая изучает вопросы уравнений и неравенств)
— Как будет называться этот способ решения? (алгебраический)
— Какими способами решались задачи? (арифметическим и алгебраическим)
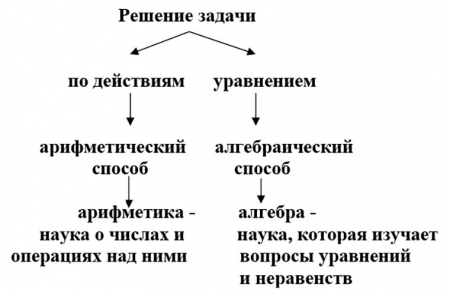
Способы решения задач
Домашнее задание
— Расспросите родителей, что они знают о Сихотэ-алинском заповеднике, о программах по сохранению популяции тигра на Земле.
— Расскажите им, что знаете вы.
Источник: koncpekt.ru