Программы с матрицами примеры

В этом пошаговом руководстве показано, как использовать C++ AMP для ускорения выполнения матричного умножения. Представлено два алгоритма: один без плитки, а второй с плиткой.

Предварительные требования

Перед началом работы

• Ознакомьтесь с обзором C++ AMP.
• См . статью Использование плиток.
• Убедитесь, что используется по крайней мере Windows 7 или Windows Server 2008 R2.

Начиная с Visual Studio 2022 версии 17.0 заголовки C++ AMP являются устаревшими. Включение всех заголовков AMP приведет к ошибкам сборки. Определите _SILENCE_AMP_DEPRECATION_WARNINGS перед включением заголовков AMP, чтобы заглушить предупреждения.

Создание проекта

Инструкции по созданию проекта зависят от установленной версии Visual Studio. Чтобы ознакомиться с документацией по предпочтительной версии Visual Studio, используйте селектор Версия. Он находится в верхней части оглавления на этой странице.

Создание проекта в Visual Studio

Матрица судьбы разборы — Финансы, программы в матрице

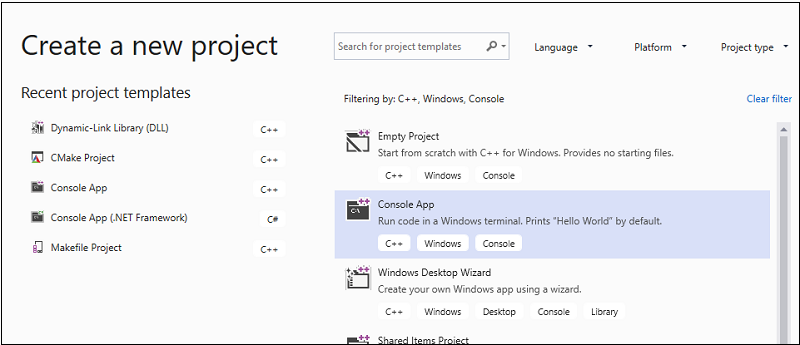
1. В строке меню выберите Файл>Создать>Проект, чтобы открыть диалоговое окно Создание проекта.
2. В верхней части диалогового окна задайте для параметра Язык значение C++, для параметра Платформа значение Windows, а для Типа проекта — Консоль.
3. Из отфильтрованного списка типов проектов выберите Пустой проект , а затем нажмите кнопку Далее. На следующей странице введите MatrixMultiply в поле Имя , чтобы указать имя проекта, и при необходимости укажите расположение проекта.
4. Нажмите кнопку Создать, чтобы создать клиентский проект.
5. В Обозреватель решений откройте контекстное меню исходных файлов и выберите Добавить>новый элемент.
6. В диалоговом окне Добавление нового элемента выберите Файл C++ (CPP), введите MatrixMultiply.cpp в поле Имя и нажмите кнопку Добавить .

Создание проекта в Visual Studio 2017 или 2015

1. В строке меню в Visual Studio выберите Файл>Новый>проект.
2. В разделе Установленные в области шаблонов выберите Visual C++.
3. Выберите Пустой проект, введите MatrixMultiply в поле Имя , а затем нажмите кнопку ОК .
4. Нажмите кнопку Далее.
5. В Обозреватель решений откройте контекстное меню исходных файлов и выберите Добавить>новый элемент.
6. В диалоговом окне Добавление нового элемента выберите Файл C++ (CPP), введите MatrixMultiply.cpp в поле Имя и нажмите кнопку Добавить .

Умножение без наложения

В этом разделе рассмотрим умножение двух матриц, A и B, которые определены следующим образом:

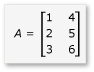
МАТРИЦЫ математика УМНОЖЕНИЕ МАТРИЦ и простейшие операции с матрицами

A — это матрица 3 на 2, а B — матрица 2 на 3. Результатом умножения A на B является следующая матрица 3 на 3. Произведение вычисляется путем умножения строк A на столбцы элемента B за элементом.

Умножение без использования C++ AMP

1. Откройте MatrixMultiply.cpp и используйте следующий код для замены существующего кода.

#include void MultiplyWithOutAMP() < int aMatrix[3][2] = , , >; int bMatrix[2][3] = , >; int product[3][3] = , , >; for (int row = 0; row < 3; row++) < for (int col = 0; col < 3; col++) < // Multiply the row of A by the column of B to get the row, column of product. for (int inner = 0; inner < 2; inner++) < product[row][col] += aMatrix[row][inner] * bMatrix[inner][col]; >std::cout std::cout > int main()

Умножение с помощью C++ AMP

1. В MatrixMultiply.cpp добавьте следующий код перед методом main .

void MultiplyWithAMP() < int aMatrix[] = < 1, 4, 2, 5, 3, 6 >; int bMatrix[] = < 7, 8, 9, 10, 11, 12 >; int productMatrix[] = < 0, 0, 0, 0, 0, 0, 0, 0, 0 >; array_view a(3, 2, aMatrix); array_view b(2, 3, bMatrix); array_view product(3, 3, productMatrix); parallel_for_each(product.extent, [=] (index idx) restrict(amp) < int row = idx[0]; int col = idx[1]; for (int inner = 0; inner >); product.synchronize(); for (int row = 0; row std::cout >
#include using namespace concurrency;
int main()

Умножение с помощью мозаика

Плитка — это способ, при котором данные секционируются на подмножества одинакового размера, которые называются плитками. При использовании плитки изменяются три вещи.

• Можно создавать tile_static переменные. Доступ к данным в tile_static пространстве может быть во много раз быстрее, чем доступ к данным в глобальном пространстве. Экземпляр переменной создается для каждой tile_static плитки, и все потоки на плитке имеют доступ к переменной. Основное преимущество плитки заключается в повышении производительности за счет tile_static доступа.
• Можно вызвать метод tile_barrier::wait , чтобы остановить все потоки в одной плитке в указанной строке кода. Вы не можете гарантировать порядок выполнения потоков, а только то, что все потоки в одной плитке остановятся при вызове , tile_barrier::wait прежде чем они продолжат выполнение.
• У вас есть доступ к индексу потока относительно всего array_view объекта и к индексу относительно плитки. С помощью локального индекса можно упростить чтение и отладку кода.

Чтобы воспользоваться преимуществами мозаичного умножения, алгоритм должен разделить матрицу на плитки, а затем скопировать данные плиток в tile_static переменные для более быстрого доступа. В этом примере матрица секционируется на подматрии одинакового размера. Продукт обнаруживается путем умножения подматрий. Две матрицы и их продукт в этом примере:

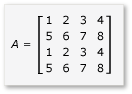
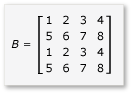
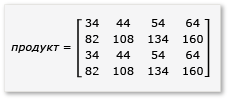
Матрицы разделены на четыре матрицы 2×2, которые определяются следующим образом:

Произведение A и B теперь можно записать и вычислить следующим образом:

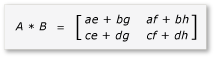
Поскольку матрицы a до h являются матрицами 2×2, все продукты и суммы из них также являются матрицами 2×2. Из этого также следует, что произведение A и B является матрицей 4×4, как и ожидалось. Чтобы быстро проверка алгоритм, вычислите значение элемента в первой строке, первом столбце в продукте. В примере это будет значение элемента в первой строке и первом столбце ae + bg . Необходимо вычислить только первый столбец, первую строку ae и bg для каждого термина. Это значение для ae равно (1 * 1) + (2 * 5) = 11 . Значение bg равно (3 * 1) + (4 * 5) = 23 . Конечное значение — 11 + 23 = 34 , что правильно.

Чтобы реализовать этот алгоритм, код:

• tiled_extent Использует объект вместо extent объекта в вызове parallel_for_each .
• tiled_index Использует объект вместо index объекта в вызове parallel_for_each .
• Создает tile_static переменные для хранения вложенных матриц.
• Использует метод , tile_barrier::wait чтобы остановить потоки для вычисления продуктов подматрицы.

Умножение с помощью AMP и плитки

1. В MatrixMultiply.cpp добавьте следующий код перед методом main .

void MultiplyWithTiling() < // The tile size is 2. static const int TS = 2; // The raw data. int aMatrix[] = < 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8 >; int bMatrix[] = < 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8 >; int productMatrix[] = < 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 >; // Create the array_view objects. array_view a(4, 4, aMatrix); array_view b(4, 4, bMatrix); array_view product(4, 4, productMatrix); // Call parallel_for_each by using 2×2 tiles. parallel_for_each(product.extent.tile(), [=] (tiled_index t_idx) restrict(amp) < // Get the location of the thread relative to the tile (row, col) // and the entire array_view (rowGlobal, colGlobal). int row = t_idx.local[0]; int col = t_idx.local[1]; int rowGlobal = t_idx.global[0]; int colGlobal = t_idx.global[1]; int sum = 0; // Given a 4×4 matrix and a 2×2 tile size, this loop executes twice for each thread. // For the first tile and the first loop, it copies a into locA and e into locB. // For the first tile and the second loop, it copies b into locA and g into locB. for (int i = 0; i < 4; i += TS) < tile_static int locA[TS][TS]; tile_static int locB[TS][TS]; locA[row][col] = a(rowGlobal, col + i); locB[row][col] = b(row + i, colGlobal); // The threads in the tile all wait here until locA and locB are filled. t_idx.barrier.wait(); // Return the product for the thread. The sum is retained across // both iterations of the loop, in effect adding the two products // together, for example, a*e. for (int k = 0; k < TS; k++) < sum += locA[row][k] * locB[k][col]; >// All threads must wait until the sums are calculated. If any threads // moved ahead, the values in locA and locB would change. t_idx.barrier.wait(); // Now go on to the next iteration of the loop. > // After both iterations of the loop, copy the sum to the product variable by using the global location. product[t_idx.global] = sum; >); // Copy the contents of product back to the productMatrix variable. product.synchronize(); for (int row = 0; row std::cout >

1. Скопируйте элементы плитки[0,0] в a locA . Скопируйте элементы плитки[0,0] в b locB . Обратите внимание, что product является плиткой, а не a и b . Поэтому для доступа a, b к и product используются глобальные индексы. Вызов имеет tile_barrier::wait важное значение. Он останавливает все потоки на плитке до заполнения и locA locB .
2. Умножьте locA и locB и поместите результаты в product .
3. Скопируйте элементы плитки[0,1] в a locA . Скопируйте элементы плитки [1,0] в b locB .
4. Умножьте locA и locB и добавьте их в результаты, которые уже находятся в product .
5. Умножение плитки[0,0] завершено.
6. Повторите для остальных четырех плиток. Специально для плиток не выполняется индексирование, и потоки могут выполняться в любом порядке. При выполнении каждого потока переменные создаются для каждой плитки соответствующим образом, tile_static а вызов управляет tile_barrier::wait потоком программы.
7. При внимательном изучении алгоритма обратите внимание, что каждая подматрикса загружается в tile_static память дважды. Передача данных занимает время. Однако после того, как данные будут в tile_static памяти, доступ к данным выполняется гораздо быстрее. Так как для вычисления продуктов требуется повторяющийся доступ к значениям в подматрисах, общий рост производительности наблюдается. Для каждого алгоритма требуется экспериментирование, чтобы найти оптимальный алгоритм и размер плитки.

В примерах, отличных от AMP и без плиток, каждый элемент A и B обращается четыре раза из глобальной памяти для вычисления продукта. В примере плитки доступ к каждому элементу осуществляется дважды из глобальной памяти и четыре раза из tile_static памяти. Это не является значительным повышением производительности. Однако если бы матрицы A и B были 1024 x 1024, а размер плитки — 16, производительность была бы значительно больше. В этом случае каждый элемент будет копироваться в tile_static память только 16 раз и обращаться из tile_static памяти 1024 раза.

Источник: learn.microsoft.com

Статические и динамические матрицы

Рассмотрим основные операции , выполняемые над матрицами (статическими и динамическими) при решении задач.

Матрицы, как и массивы, нужно вводить (выводить) поэлементно. Блок- схема ввода элементов матрицы x[n][m] изображена на рис. 6.3.

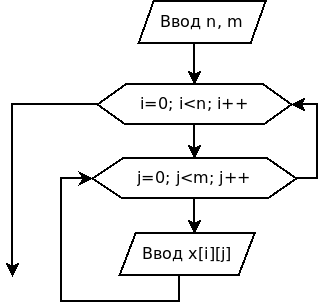
Рис. 6.3. Ввод элементов матрицы

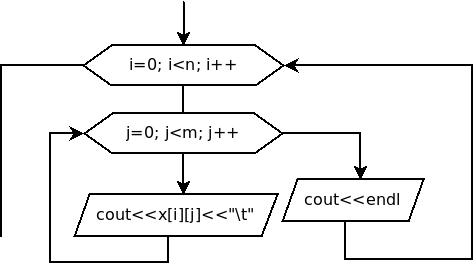
Рис. 6.4. Блок-схема построчного вывода матрицы

При выводе матрицы элементы располагаются построчно, например:

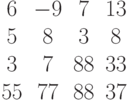
Алгоритм построчного вывода элементов матрицы приведён на рис. 6.4.

Ниже приведён текст программы на C++ ввода-вывода статической матрицы.

#include using namespace std; int main ( ) < int i, j,N,M, a [ 20 ] [ 20 ]; cout>N; //Ввод количества строк cout>M; //Ввод количества столбцов cout>a [ i ] [ j ]; //Ввод очередного элемента матрицы cout >

Цикл для построчного вывода матрицы можно записать и так.

for ( i =0; i

При вводе матрицы элементы каждой строки можно разделять пробелами, символами табуляции или Enter . Ниже представлены результаты работы программы.

N=4 M=5 Ввод матрицы A 1 2 3 5 4 3 6 7 8 9 1 2 3 4 5 6 7 8 9 0 Вывод матрицы A 1 2 3 5 4 3 6 7 8 9 1 2 3 4 5 6 7 8 9 0

Далее на примерах решения практических задач будут рассмотрены основные алгоритмы обработки матриц и их реализация в C++ . Перед этим давайте вспомним некоторые свойства матриц (рис. 6.5):

• если номер строки элемента совпадает с номером столбца (), это означает, что элемент лежит на главной диагонали матрицы;
• если номер строки превышает номер столбца ( 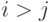), то элемент находится ниже главной диагонали;
• если номер столбца больше номера строки (i < j), то элемент находится выше главной диагонали.
• элемент лежит на побочной диагонали, если его индексы удовлетворяют равенству ;
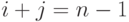• неравенство i + j < n — 1 характерно для элемента, находящегося выше побочной диагонали;
• соответственно, элементу лежащему ниже побочной диагонали соответствует выражение .

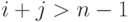Источник: intuit.ru

Умножение матриц

Умножение матриц – одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведением матриц.

Описание алгоритма

Для матриц A и B:

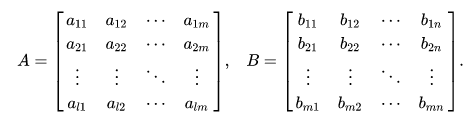
Произведением называют матрицу C:

В которой каждый элемент вычисляется по формуле:

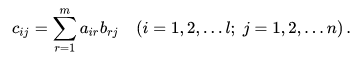
Произведение двух матриц выполнимо только в случае, если количество столбцов левой матрицы равно количеству строк правой.

Реализация алгоритма

using System; // класс с методами расширения static class MatrixExt < // метод расширения для получения количества строк матрицы public static int RowsCount(this int[,] matrix) < return matrix.GetUpperBound(0) + 1; > // метод расширения для получения количества столбцов матрицы public static int ColumnsCount(this int[,] matrix) < return matrix.GetUpperBound(1) + 1; > > class Program < // метод для получения матрицы из консоли static int[,] GetMatrixFromConsole(string name) < Console.Write(«Количество строк матрицы : «, name); var n = int.Parse(Console.ReadLine()); Console.Write(«Количество столбцов матрицы : «, name); var m = int.Parse(Console.ReadLine()); var matrix = new int[n, m]; for (var i = 0; i < n; i++) < for (var j = 0; j < m; j++) < Console.Write(«[,] hljs-keyword»>int.Parse(Console.ReadLine()); > > return matrix; > // метод для печати матрицы в консоль static void PrintMatrix(int[,] matrix) < for (var i = 0; i < matrix.RowsCount(); i++) < for (var j = 0; j < matrix.ColumnsCount(); j++) < Console.Write(matrix[i, j].ToString().PadLeft(4)); > Console.WriteLine(); > > // метод для умножения матриц static int[,] MatrixMultiplication(int[,] matrixA, int[,] matrixB) < if (matrixA.ColumnsCount() != matrixB.RowsCount()) < throw new Exception(«Умножение не возможно! Количество столбцов первой матрицы не равно количеству строк второй матрицы.»); > var matrixC = new int[matrixA.RowsCount(), matrixB.ColumnsCount()]; for (var i = 0; i < matrixA.RowsCount(); i++) < for (var j = 0; j < matrixB.ColumnsCount(); j++) < matrixC[i, j] = 0; for (var k = 0; k < matrixA.ColumnsCount(); k++) < matrixC[i, j] += matrixA[i, k] * matrixB[k, j]; >> > return matrixC; > static void Main(string[] args) < Console.WriteLine(«Программа для умножения матриц»); var a = GetMatrixFromConsole(«A»); var b = GetMatrixFromConsole(«B»); Console.WriteLine(«Матрица A:»); PrintMatrix(a); Console.WriteLine(«Матрица B:»); PrintMatrix(b); var result = MatrixMultiplication(a, b); Console.WriteLine(«Произведение матриц:»); PrintMatrix(result); Console.ReadLine(); > >

Источник: programm.top