Решение нелинейных уравнений на языке программирования Pascal
Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Из этой статьи вы узнаете о наиболее известных алгоритмах численного решения уравнений. Практически все они могут быть разделены на два этапа: отделения и уточнения корней.
Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.
Наиболее простым в реализации является метод бисекции, или как его еще называют, метод половинного деления. Это итерационный метод, суть которого заключается в том, что на каждой итерации интервал сокращается вдвое до тех пор, пока не будет найдено решение с заданной точностью.
Программы паскаль численные методы
Nickolay.info. Обучение. Библиотека численных методов на Паскале
Метод простых итераций — Pascal
Материал публикуется в связи с сессией, так как многие не просто изучают численные методы, но еще и программируют их на старом добром Паскале 🙂 В помощь таким страждущим студентам — наша старая добрая (конца XX века) бибилиотека численных методов на Паскале.
Сами численные методы реализованы в библиотеке LPM2.TPU (исходник в соответствующем файле .PAS), все остальные файлы с расширением .PAS — демки для вызовов разных функций библиотеки. Паскаль версии 7.1 можно взять на этой странице сайта.
Скиньте все файлы *.pas из архива в удобную папку, а скомпилированную библиотеку lpm2.tpu — в папку, которая указана в настройке Options -> Unit Directories верхнего меню Паскаля. Затем открывайте и запускайте нужные программы.
- EMPIRICH.PAS — эмпирическая зависимость по массивам X,Y переменной размерности (*).
- FPRM.PAS — определённый интеграл методом средних прямоугольников. Задаются пределы интегрирования a,b, число узловых точек n, в коде определяется функция f(x).
- FSIMP.PAS — определённый интеграл методом Симпсона. Данные задаются, как для модуля FPRM, плюс требуемая точность.
- FTRAP.PAS — определённый интеграл методом трапеций. Данные задаются, как для модуля FPRM.
- INTER.PAS — реализация первой и второй интерполяционной формулы Ньютона. вводятся размер таблицы, массивы значений X и Y, значение аргумента для интерполяционной формулы и номер формулы (1 или 2).
- KLGRAPH.PAS — графопостроитель по данным массивов X,Y. Задаются целочисленные ширина и высота сетки (по сути дела, они обозначают размеры картинки в пикселах), количество горизонтальных и вертикальных осей (ячеек сетки), размер таблицы, затем массивы данных X и Y (могут быть вещественными).
- MITER.PAS — метод итераций решения уравнения. Функция уравнения задана программно как F(X)=D1*x*x*x+D2*x*x+D3*x+D4, вводятся коэффийиенты D1,D2,D3,D4, начальное приближение для x, константа метода и желаемая точность вычисления.
- MNEWTON.PAS — метод Ньютона для решения уравнения. Данные вводятся как для MITER (кроме константы метода).
- ODY1.PAS — обыкновенное дифференциальное уравнение 1 порядка, методы Эйлера (обычный и модифицированный), Рунге-Кутта. Вводятся интервал [a,b], шаг разностной сетки, начальное условие. Функция задается подпрограммой F(X,y). (*).
- ODY2.PAS — обыкновенное дифференциальное уравнение 2 порядка. Вводятся коэффициенты уравнения P,G,F, коэффициенты 1-го и 2-го краевых условий, интервал [a,b], шаг разностной сетки. Функции программируются подпрограммами P1(x), G1(x), F1(x) (*).
- ODY22.PAS — модификация ODY2, не имеет самостоятельного значения (*).
- OPT.PAS — методы оптимизации. Поиск экстремумов унимодальных функций одной переменной. Функция задается подпрограммой F(x). Реализованы методы равномерного поиска, поразрядного приближения, дихотомии (половинного деления), золотого сечения. (*)
- PROG.PAS — решение системы линейных алгебраических уравнений (СЛАУ) методом прогонки. Вводятся порядок системы, матрица коэффициентов системы, вектор свободных членов.
- TGRAPH.PAS — построение графика функции, заданной подпрограммой F(X). Вводятся ширина и высота сетки (по сути дела, размеры картинки графика в пикселах), число горизонтальных и вертикальных осей (линий сетки), интервал построения графика. (*)
- ZEID.PAS — решение системы линейных алгебраических уравнений (СЛАУ) методом Зейделя. Вводятся порядок системы, матрица коэффициентов системы, вектор свободных членов, точность вычисления, максимальное число итераций.
Здесь (*) означает, что предполагается переход в графический режим для вывода картинки.
Метод Ньютона (метод касательных) Пример Решения
Если Ваш компьютер — такой новый, что уже не показывает DOS-графику, поставьте DOSBox и DOSShell (ссылка есть внизу этой страницы сайта). Тогда Вы сможете скомпилировать в Паскале исполняемый файл (включив в Паскале настройку верхнего меню Compile -> Destination в значение Disk) и потом запустить его из DOSBox или DOSShell.
Еще более простое решение — воспользуйтесь для таких программ файлом menu.bat из вложенной в архив папки EXE (возможно, запускать его придется все-таки из-под DOSShell, зато он покажет все русскоязычные подписи в DOS-графике и т.п.). Для Ваших собственных функций измените текст нужного модуля, перекомпилируйте его на диск и скопируйте в папку EXE.
Скачать:
Библиотека численных методов на Паскале,202 Кб, архив *.ZIP с программами
Подробная дока к библиотеке, 23 Кб, архив *.ZIP с документом Word
Источник: nickolay.info
Численные методы. Программа-калькулятор на Pascal
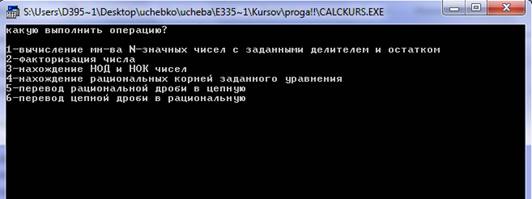
Разработать программу-калькулятор CalcKurs на языке программирования Pascal, реализующую следующие функции:
1. формирование заданного подмножества натурального ряда с помощью общего делителя;
2. факторизация числа с опциями;
3. нахождение НОД и НОК для заданной совокупности натурального ряда;
4. нахождение рациональных решений уравнения с целочисленными коэффициентами;
5. представление рациональной дроби в виде цепной;
6. представление цепной дроби в виде рациональной.
Оборудование и ПО:
Название Windows: Windows Seven (6.1.7600) Ultimate
Установлено памяти: 1 022,49 MB
Среда программирования: Turbo Pascal 7.0
2. Специальная часть
2.1 Интерфейс программы
2.2 Описание процедур
4. Список использованных источников
Теория чисел — это одно из направлений математики, которое иногда называют «высшей арифметикой». Данная наука изучает натуральные числа и некоторые сходные с ними объекты, рассматривает различные свойства (делимость, разложимость, взаимосвязи и так далее), алгоритмы поиска чисел, а также определяет ряд достаточно интересных наборов натуральных чисел.
Так, к примеру, в рамках теории чисел рассматриваются вопросы делимости целых чисел друг на друга, алгоритм Евклида для поиска наибольшего общего делителя, поиск наименьшего общего кратного, малая и большая теоремы Ферма. В качестве самых известных рядов натуральных чисел можно привести ряд Фибоначчи, простые числа, совершенные и дружественные числа, степени и суперстепени натуральных чисел. [1]
Вне самой математики теория чисел имеет довольно мало приложений, и развивалась она не ради решения прикладных задач, а как искусство ради искусства, обладающее своей внутренней красотой, тонкостью и трудностью. Тем не менее теория чисел оказала большое влияние на математическую науку, поскольку некоторые разделы математики (в том числе и такие, которые впоследствии нашли применение в физике) были первоначально созданы для решения особенно сложных проблем теории чисел. [2]
Разработанная программа включает в себя набор из нескольких основных операций, которые могут понадобиться при решении более сложных задач.
Назначение программы CalcKurs
Программа CalcKurs выполняет следующие функции:
1.формирование заданного подмножества натурального ряда с помощью общего делителя;
2.факторизация числа с опциями;
3.нахождение НОД и НОК для заданной совокупности натурального ряда;
4.нахождение рациональных решений уравнения с целочисленными коэффициентами;
5.представление рациональной дроби в виде цепной;
6.представление цепной дроби в виде рациональной.
2. СПЕЦИАЛЬНАЯ ЧАСТЬ
Описание процедур procedure DelOstatok
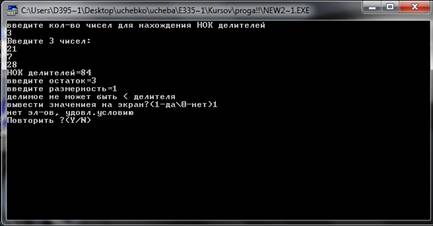
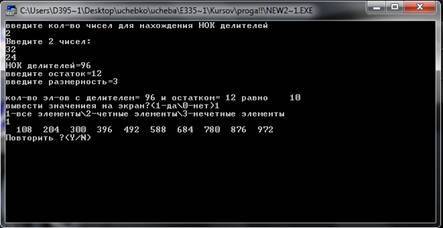
Данная процедура формирует заданное подмножество натурального ряда с помощью общего делителя.
Ищется общий делитель совокупности делителей (общий делитель ищется с помощью нахождения наименьшего общего кратного делителей). На заданном множестве (кол-во цифр в числах) ищем первый элемент, который будет удовлетворять заданному условию (делится на НОК с остатком), запоминаем элемент и прерываем цикл.
Формируем подмножество с помощью прибавления к первому элементу делителя, суммируем количество элементов, пока элементы не станут больше заданной размерности.
Делитель=10, остаток=3, размерность=2 (от 10 до 99)
Данная процедура выполняет факторизацию (разложение на простые множители) числа с опциями.
Ищем для данного числа простой множитель с помощью решета Эратосфена [3]
(Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:
1. Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).
2. Пусть переменная p изначально равна двум — первому простому числу.
3. Вычеркнуть из списка все числа от 2p до n, делящиеся на p (то есть, числа 2p, 3p, 4p, …)
4. Найти первое не вычеркнутое число, большее чем p, и присвоить значению переменной p это число.
5. Повторять шаги 3 и 4 до тех пор, пока p не станет больше, чем n
6. Все не вычеркнутые числа в списке — простые числа.)
и делим заданное число на данный множитель, потом ищем следующий простой множитель(если он повторяется, то возводим его в степень), и так до тех пор, пока число не станет равным единице. Записываем все простые множители.
Далее находим все делители числа и составляем из них множество. Вычисляем сумму делителей.
множество делителей=1 3 7 21
кол-во простых множителей=2
Источник: kazedu.com