Программы для численное решение дифференциальных уравнений

Содержание

Создавая дополнения к отечественной математической программе SMath Studio, я нашёл в сети ряд библиотек, которые можно было бы использовать в своих программах. Предлагаю небольшой их обзор.

Стандартный RK45 с фиксированным шагом может помочь в большинстве случаев, но бывают задачи, где этого недостаточно. Для решения жёстких систем были придуманы специальные решатели, которые мы и рассмотрим с точки зрения их практического использования.

Большинство представленных ниже функций, если не оговорено особо, можно привести к одному формату вызова (по аналогии с Mathcad):

ode_solver( init, x1, x2, intvls, D(t, x) )

init — вектор начальных условий,
(x1, x2) — отрезок интегрирования,
intvls — количество интервалов на отрезке,
D(t, x) — система ОДУ.

1. Intel ODE Solvers Library

Содержит следующие функции: rkm9st(), mk52lfn(), mk52lfa(), rkm9mkn(), rkm9mka().

rkm9st() — a specialized routine for solving non-stiff and middle-stiff ODE systems using the explicit method, which is based on the 4th order Merson’s method and the 1st order multistage method of up to and including 9 stages with stability control.
mk52lfn() — a specialized routine for solving stiff ODE systems using the implicit method based on L-stable (5,2)-method with the numerical Jacobi matrix, which is computed by the routine.
mk52lfa() — a specialized routine for solving stiff ODE systems using the implicit method based on L-stable (5,2)-method with numerical or analytical computation of the Jacobi matrix. The user must provide a routine for this computation.
rkm9mkn() — a specialized routine for solving ODE systems with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step and computes the numerical Jacobi matrix when necessary.
rkm9mka() — a specialized routine for solving ODE systems with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step. The user must provide a routine for numerical or analytical computation of the Jacobi matrix.

intel_ode.h

Численное решение обыкновенных дифференциальных уравнений методом Эйлера

/******************************************************************************* ! INTEL CONFIDENTIAL ! Copyright(C) 2007-2008 Intel Corporation. All Rights Reserved. ! The source code contained or described herein and all documents related to ! the source code («Material») are owned by Intel Corporation or its suppliers ! or licensors. Title to the Material remains with Intel Corporation or its ! suppliers and licensors. The Material contains trade secrets and proprietary ! and confidential information of Intel or its suppliers and licensors. The ! Material is protected by worldwide copyright and trade secret laws and ! treaty provisions.

2. GNU Scientific Library (GSL)

Содержит следующие функции: rk2(), rk4(), rkf45(), rkck(), rk8pd(), rk1imp(), rk2imp(), rk4imp(), bsimp(), msadams(), msbdf().

Часть из них требует дополнительные параметры для работы (Якобиан). Те, которые мне удалось привести к общему виду:

Solvers for Non-Stiff Systems:

rk2() — explicit embedded Runge-Kutta (2, 3) method.
rk4() — explicit 4th order (classical) Runge-Kutta. Error estimation is carried out by the step doubling method.
rkf45() — explicit embedded Runge-Kutta-Fehlberg (4, 5) method.
rkck() — explicit embedded Runge-Kutta Cash-Karp (4, 5) method.
rk8pd() — explicit embedded Runge-Kutta Prince-Dormand (8, 9) method.

rk1imp() — Implicit Gaussian first order Runge-Kutta. Also known as implicit Euler or backward Euler method. Error estimation is carried out by the step doubling method. This algorithm requires the Jacobian.
rk2imp() — Implicit Gaussian second order Runge-Kutta. Also known as implicit mid-point rule. Error estimation is carried out by the step doubling method. This stepper requires the Jacobian.
rk4imp() — Implicit Gaussian 4th order Runge-Kutta. Error estimation is carried out by the step doubling method. This algorithm requires the Jacobian.
bsimp() — Implicit Bulirsch-Stoer method of Bader and Deuflhard. The method is generally suitable for stiff problems. This stepper requires the Jacobian.
msadams() — A variable-coefficient linear multistep Adams method in Nordsieck form. This stepper uses explicit Adams-Bashforth (predictor) and implicit Adams-Moulton (corrector) methods in P(EC)^m functional iteration mode. Method order varies dynamically between 1 and 12.
msbdf() — A variable-coefficient linear multistep backward differentiation formula (BDF) method in Nordsieck form. This stepper uses the explicit BDF formula as predictor and implicit BDF formula as corrector. A modified Newton iteration method is used to solve the system of non-linear equations. Method order varies dynamically between 1 and 5. The method is generally suitable for stiff problems. This stepper requires the Jacobian.

3. Matlab C++ Math Library 2.1 (Win32)

Да, вы можете использовать эту старую версию run-time библиотек для расчётов. Более того, она может быть установлена по относительным путям, т.е. можно просто положить содержимое оригинального дистрибутива (~28 Мб в развёрнутом виде) рядом со своей программой. Правда при вызове функций придётся использовать SetCurrentDirectory() с прямым указанием на место расположения «binwin32». Я так делаю в своём дополнении.

Содержит следующие функции: ode23(), ode45(), ode113(), ode15s(), ode23s().

ode23() — solve nonstiff differential equations; low order method,
ode45() — solve nonstiff differential equations; medium order method,
ode113() — solve nonstiff differential equations; variable order method,
ode15s() — solve stiff differential equations and DAEs; variable order method,
ode23s() — solve stiff differential equations; low order method.

4. Octave C++ Math Library (Win32)

Примерно то же самое, что и Matlab C++ Math Library, но со своими тараканами. К сожалению, работу с этой библиотекой я одолел только частично. Дополнение OctaveCppMathLibrary демонстрирует работу с этой библиотекой из c# кода.

5. DotNumerics

Содержит следующие функции: AdamsMoulton(), ExplicitRK45(), ImplicitRK5(), GearsBDF(). Эта библиотека портирована для .Net с фортрана. Она понравилась мне больше всего. Работает достаточно быстро.

Solvers for Non-Stiff Systems:

AdamsMoulton() — solves an initial-value problem for nonstiff ordinary differential equations using the Adams-Moulton method.
ExplicitRK45() — solves an initial-value problem for nonstiff ordinary differential equations using the explicit Runge-Kutta method of order (4)5.

ImplicitRK5() — solves an initial-value problem for stiff ordinary differential equations using the implicit Runge-Kutta method of order 5.
GearsBDF() — solves an initial-value problem for stiff ordinary differential equations using the Gear’s BDF method.

Как выглядит модель амплитудного детектора в SMath Studio при решении ОДУ с помощью функции GearsBDF():

SMath Studio

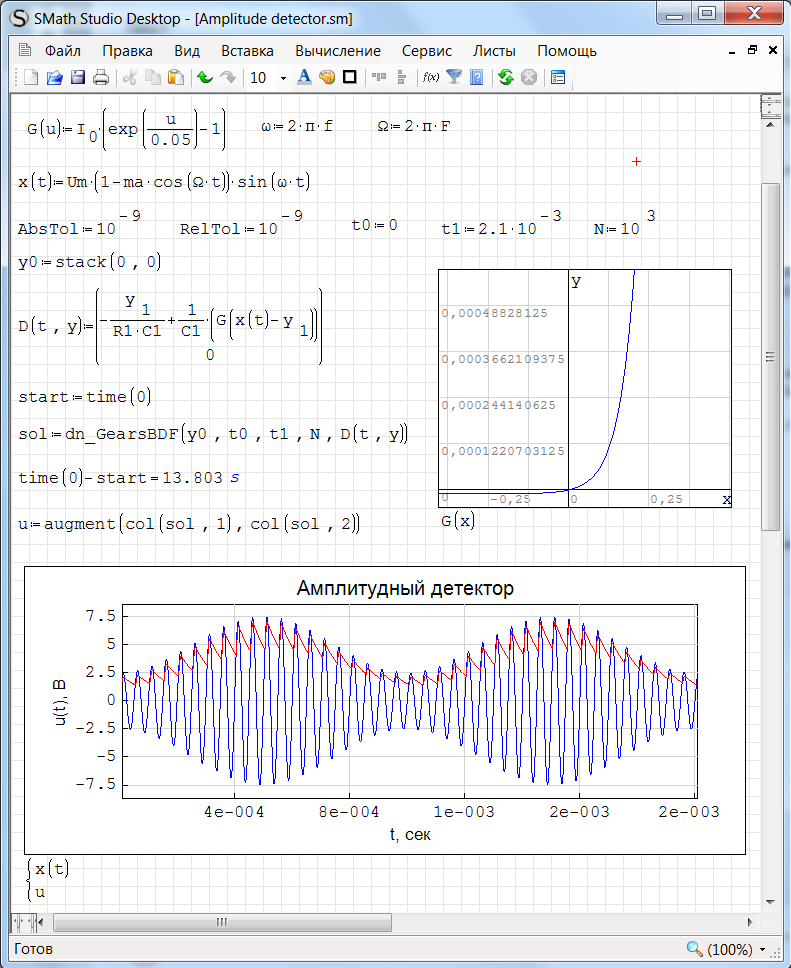
Обновление (12.07.2014).

6. boost::odeint

Содержит следующие алгоритмы:

Explicit Euler
Modified Midpoint
Runge-Kutta 4
Cash-Karp
Dormand-Prince 5
Fehlberg 78
Adams Bashforth
Adams Moulton
Adams Bashforth Moulton
Controlled Runge-Kutta
Dense Output Runge-Kutta
Bulirsch-Stoer
Bulirsch-Stoer Dense Output
Implicit Euler
Rosenbrock 4
Controlled Rosenbrock 4
Dense Output Rosenbrock 4
Symplectic Euler
Symplectic RKN McLachlan
Symplectic RKN McLachlan

7. SADEL (Sets of Algebraic and Differential Equations solvers Library)

Живьём не пробовал, показать пример использования не могу.

8. Решатель Лимонова А. Г.

Живьём не пробовал, показать пример использования не могу.

Источник: habr.com

Русские Блоги

C ++ программа для численного решения обыкновенных дифференциальных уравнений методом Эйлера, методом прогнозной коррекции (улучшенный метод Эйлера) и методом Рунге-Кутты четвертого порядка

#include using namespace std; double cor[10000]; double f (double x, double y) // функция перезаписи < return x+y; >double correctf (double x) // функция точного решения < return -x-1+2*exp(x); >void Эйлер (double h, double l, double r, double * a, double * b, double tol) // Метод Эйлера < double sum=0; for(int i=1; ifor(int i=1; i void улучшенныйEuler (double h, double l, double r, double * a, double * b, double tol) // Улучшенный метод Эйлера < double b1,sum=0; for(int i=1; ifor(int i=1; i void RungeKutta (double h, double l, double r, double * a, double * b, double tol) // Метод RungeKutta четвертого порядка < double k1,k2,k3,k4,sum=0; for(int i=1; ifor(int i=1; i int main() < double h,a[10000],b[10000],l,r; memset(a,0,sizeof(a)); memset(b,0,sizeof(b)); memset(cor,0,sizeof(cor)); printf («Пожалуйста, введите размер шага:»); scanf(«%lf», printf («Пожалуйста, введите нижний предел интервала:»); scanf(«%lf», printf («Пожалуйста, введите верхний предел интервала:»); scanf(«%lf», printf («Пожалуйста, назначьте начальное значение:»); scanf(«%lf», double tol=(r-l)/h; for(int i=0; i

Интеллектуальная рекомендация

Чтение «CSS World» Xiaoji 4.1.1 Глава 4.1.1

Предисловие Эта глава имеет смысл. По сравнению с первыми тремя главами, она немного длинная. Я все еще хотел написать ее, но я писал слишком долго за раз, но большинство из них были наклейками и кодо.

Fuchsia Learn-Banjo-tutorial.md (ниже)

Стиль языка C ++ C ++ немного сложнее, чем версия языка C. Давайте взглянем. Переводчик банджо генерирует три файла 1. Первый файл был введен в языковой версии C. Два других файла находятся в каталоге.

Ответ широковещательной передачи ARP

Ранее считалось, что запрос является широковещательным, а ответ одноадресным. Но когда я сегодня работал над проектом по синтаксическому анализу пакетов данных arp, начальник (ps: богоподобное существ.

Используйте express4 и socket.io для создания сервера

Сначала установите express4, обратитесь к http://www.expressjs.com.cn/starter/generator.html Затем создайте экспресс-проект Это создает проект экспресс-фоновой службы на основе шаблона ejs. Следующая .

Общие команды Ansible (специальные команды)

Ansible предоставляет два способа выполнения задач: один — это специальные команды, а другой — написание сборников пьес Ansible. Первый может решать некоторые простые задачи, а второй — более сложные .

Источник: russianblogs.com

Метод Рунге — Кутты

Этот онлайн калькулятор реализует классический метод Рунге — Кутты (встречается также название метод Рунге — Кутта) четвертого порядка точности. Метод используется для решения дифференциальных уравнений первой степени с заданным начальным значением

Калькулятор ниже находит численное решение дифференциального уравнения первой степени методом Рунге-Кутты (иногда встречается название метод Рунге-Кутта, а в поисковиках бывает ищут «метод рунге кута», «метод рунги кутта» и даже «метод рунги кута»), который также известен как классический метод Рунге — Кутты (потому что есть на самом деле семейство методов Рунге-Кутты) или метод Рунге — Кутты четвертого порядка.

Для того, чтобы использовать калькулятор, вам надо привести дифференциальное уравнение к форме

и ввести правую часть уравнения f(x,y) в поле y’ калькулятора.

Также вам понадобится ввести начальное значение

и указать точку в которой вы хотите получить численное решение уравнения .

Последнее параметр калькулятора — размер шага с которым вычисляется следующее приближение по графику функции.

Описание метода можно найти под калькулятором.

Источник: planetcalc.ru

1. Intel ODE Solvers Library

2. GNU Scientific Library (GSL)

3. Matlab C++ Math Library 2.1 (Win32)

4. Octave C++ Math Library (Win32)

5. DotNumerics

Обновление (12.07.2014).

6. boost::odeint

7. SADEL (Sets of Algebraic and Differential Equations solvers Library)

8. Решатель Лимонова А. Г.

Русские Блоги

Интеллектуальная рекомендация

Чтение «CSS World» Xiaoji 4.1.1 Глава 4.1.1

Fuchsia Learn-Banjo-tutorial.md (ниже)

Ответ широковещательной передачи ARP

Используйте express4 и socket.io для создания сервера

Общие команды Ansible (специальные команды)

Метод Рунге — Кутты

Составьте блок схему и программу вычисления значения функции вариант 3

Напиши программу которая в последовательности натуральных чисел определяет количество чисел кратных

Как записать музыку на сд диск в формате сд программа

Какая нужна программа на телефон чтобы скачивать музыку на телефон

Если не хватает места на диске с для установки программы

Задачи по ознакомлению с формой и геометрическими фигурами в программе радуга

Как расширение имени файла связано с форматом файла и программой обработки

Что программа 12111 переводит число 50 в число 20 определите значение b