Алгоритмы можно записывать разными способами, называемыми формой представления алгоритма. На практике наиболее распространены следующие формы представления алгоритмов:
· словесная (записи на естественном языке);
· графическая (изображения из графических символов);
· псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);
· программная (тексты на языках программирования).
Словесная форма представления алгоритмов
Словесная форма записи не так широко распространена в литературе из-за ее многословности и отсутствия наглядности.
Пример 1. Алгоритм поиска наибольшего общего делителя двух чисел (НОД), известного как алгоритм Евклида.
Условие задачи — даны два целых положительных числа M и N. Найти их наибольший общий делитель.
1. Сравнить M и N.
2. Если M=N, то алгоритм закончен; N — наибольший общий делитель.
Формы записи алгоритмов | Информатика 6 класс #20 | Инфоурок
3. Если M>N, то заменим M = M — N, иначе N =N — M. Перейти к шагу 1.
Пример 2. Запись в словесной форме алгоритма нахождения максимального из двух значений.
Определим форматы переменных X, Y, M, где X и Y – значения для сравнения, M – переменная для хранения максимального значения.
1. Получим два значения чисел X и Y для сравнения.
2. Сравним X и Y.
3. Если X меньше Y, значит большее число Y.
4. Поместим в переменную M значение Y.
5. Если X не меньше (больше) Y, значит большее число X.
6. Поместим в переменную M значение X.
Словесный способ описания обладает рядом недостатков: описание строго не формализуемо, запись получается многословной, отдельные предписания (действия) допускают неоднозначность толкования.
Графический способ представления алгоритмов.
Можно выделить два способа графического представления алгоритма:
- Блок-схема.
- Диаграмма Насси – Шнейдермана.
Структурная (блок-) схема алгоритма – графическое изображение алгоритма в виде схемы связанных между собой с помощью стрелок (линий перехода) блоков – графических символов, каждый из которых соответствует одному шагу алгоритма. Внутри каждого блока дается описание соответствующего действия.
Элементы языка блок — схем
| Название символа | Обозначение и пример заполнения | Пояснение |
| Процесс (действие) |  |
Вычислительное действие или последовательность действий |
| Решение (условие) | 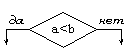 |
Проверка условий |
| Модификация |  |
Начало цикла |
| Предопределенный процесс |  |
Вычисления по подпрограмме, стандартной подпрограмме |
| Ввод-вывод |  |
Ввод-вывод в общем виде |
| Пуск-останов |  |
Начало, конец алгоритма, вход и выход в подпрограмму |
| Документ |  |
Вывод результатов на печать |
Блок «процесс» применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.
Блок «решение» используется для обозначения переходов управления по условию. В каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок «модификация» используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
Блок «предопределенный процесс» используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.
Ниже приведена блок — схема алгоритма нахождения максимального из двух значений.
Принцип программирования «сверху вниз» (когда задача решается от общего к частному, крупные задачи разбиваются на более мелкие и т.д. пока для каждой не найдется простого решения) требует, чтобы блок-схема поэтапно конкретизировалась и каждый блок «расписывался» до элементарных операций. Но такой подход можно осуществить при решении несложных задач. При решении сколько-нибудь серьезной задачи блок-схема «расползется» до такой степени, что ее невозможно будет охватить одним взглядом.
Блок-схемы алгоритмов удобно использовать для объяснения работы уже готового алгоритма, при этом в качестве блоков берутся действительно блоки алгоритма, работа которых не требует пояснений. Блок-схема алгоритма должна служить для упрощения изображения алгоритма, а не для усложнения.
Графическое изображение алгоритма широко используется перед программированием задачи вследствие его наглядности, т.к. зрительное восприятие обычно облегчает процесс написания программы, ее корректировки при возможных ошибках, осмысливание процесса обработки информации.

Рис. 4. Блок – схема алгоритма поиска максимального из двух чисел
Менее известен второй способ графического представления алгоритма — диаграмма Насси – Шнейдермана (ее также называют “диаграммой Нэсси – Шнейдермана”, “N – S-диаграммой” или “структурограммой”).
В своей статье «Краткая история структурных блок-схем (диаграмм Насси – Шнейдермана)» [4] один из авторов диаграммы Бен Шнейдерман пишет: «Пленительная история и эволюция структурных блок-схем (обычно называемых диаграммами Насси – Шнейдермана, или структурограммами) восходит к 1972 году». Далее он рассказывает, что впервые подумал о создании своих способов записи алгоритмов во время посещения лекции по структурному программированию, когда еще учился в магистратуре.
Ему пришло в голову, что если оператор GOTO не должен использоваться, то так же не нужны и соединительные линии в старых блок-схемах. Пятнадцать минут вычерчивания привели к первым идеям по оформлению следования, ветвления и циклов. Вместе с аспирантом Исааком Насси, в то время более глубоко знавшим принципы структурного программирования, они написали статью «Технологии блок-схем для структурного программирования», в которой описали свои идеи и представили новый вид графической записи алгоритмов. Статья была опубликована в августе 1973 года.
С тех пор N – S-диаграммы широко используются в ряде стран. Например, в Германии их применение при документировании программ обусловлено требованиями государственного стандарта этой страны.
Диаграммы Насси – Шнейдермана строятся с использованием шести элементарных «строительных блоков».
1. Блок действия
Как известно, алгоритм состоит из последовательности действий. Блок действия используется для представления отдельного действия алгоритма:
Рис. 5. Блоки отдельных действий.
Два действия представляют собой два блока, следующих один за другим:
Рис. 6. Блок действия.
2. Блоки с разветвлением
Блок с разветвлением используется, когда в алгоритме возможны два варианта действий, а выбор того или иного варианта действия зависит от некоторого условия:

Рис. 7. Блок с разветвлением.
Такая алгоритмическая конструкция (ветвление) представляется двумя смежными блоками действий; действие слева выполняется, если условие истинно, действие справа — если условие ложно. Например:
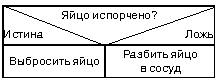
Рис. 8. Пример оформления блока — ветвления.
Возможно также неполное ветвление, при котором некоторое действие выполняется не всегда, а только при определенном условии:

Рис. 9. Блок – неполное ветвление.
3. Блок множественного выбора
Блок множественного выбора используется, когда существует несколько вариантов возможных действий, выбор которых зависит от значения некоторого выражения:
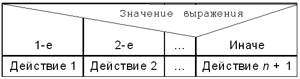
Рис. 10. Блок множественного выбора.
Например, в задаче выбора разных видов обуви для разных видов спорта:
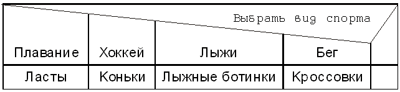
Рис. 11. Пример блока множественного выбора.
4. Блок цикла с предусловием
Блок цикла с предусловием используется тогда, когда должна быть многократно выполнена некоторая последовательность действий, причем перед каждым выполнением проверяется некоторое условие:

Рис. 12. Блок цикла с предусловием.
Действия, которые повторяются (так называемое “тело цикла”), представлены самостоятельным блоком внутри блока цикла с предусловием. Например: «Накачать спущенную велосипедную шину»:
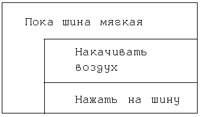
Рис. 13. Пример блока цикла с предусловием.
Так как условие проверяется перед выполнением тела цикла, возможно, действия не будут выполнены ни разу (если условие ложно в самом начале, вы немедленно выходите из цикла).
Цикл с заданным количеством повторений тела цикла (в языках программирования его называют «цикл с параметром» или «цикл со счетчиком») — это тоже цикл с предусловием. Действия повторяются определенное количество раз и отсчитываются перед каждым выполнением. Например, разбить в миску шесть яиц:

Рис. 14. Блок цикла с заданным количеством повторений.
Подсчет действий происходит в начале. Так, если бы вы считали вслух, вы бы сказали «один» перед тем, как разбить первое яйцо.
5. Блок цикла с постусловием
Блок цикла с постусловием используется, когда в алгоритме действия должны повторяться до наступления определенного условия (условие проверяется после выполнения действий):

Рис. 15. Блок цикла с постусловием.
Например, в задаче приготовления теста для блинов:

Рис. 16. Пример блока цикла с постусловием.
Действия в цикле с постусловием всегда выполняются хотя бы один раз, потому что проверка осуществляется в конце цикла. Так, при приготовлении теста для блинов немного молока будет добавлено и размешано до того, как будет проверена консистенция теста.
6. Блок подпрограммы

Рис. 17. Блок подпрограммы.
Блок подпрограммы используется в случаях, когда некоторый процесс в алгоритме слишком большой, чтобы изображать его на диаграмме, или когда какие-то блоки действий используются несколько раз в разных местах одной и той же диаграммы. Например, для задачи стрижки газона около дома диаграмма алгоритма ее решения может быть оформлена так:
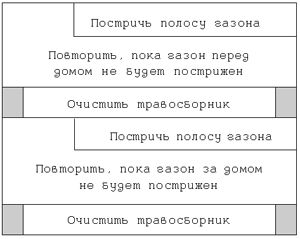
Рис. 18. Пример алгоритма с подпрограммами.
Диаграмма, иллюстрирующая действия в подпрограмме, оформляется отдельно.
Подпрограмма “Очистить травосборник”

Рис. 19. Пример блока — подпрограммы.
Очевидные преимущества N – S-диаграмм заключаются в:
2. отсутствии соединительных линий со стрелками, что помогает избежать случайных ошибок;
3. компактности, т.к. даже относительно длинный алгоритм на языке N–S-диаграмм несложно разместить на одной странице;
4. простоте использования.
Перечисленные блоки могут произвольным образом вкладываться один в другой. Проиллюстрируем сказанное на примере задачи: «Найти наименьшее число в следующей последовательности чисел: 51 25 35 79 13 26 65».
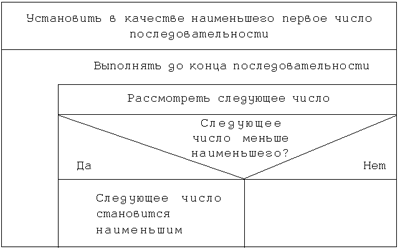
Рис. 20. Диаграмма Насси – Шнейдермана для задачи поиска минимального числа в последовательности.
Если проверить работу этого алгоритма на примере последовательности чисел: 51 25 35 79 13 26, то получим наименьшее число в последовательности — 13.
Еще один пример построения структурограммы.
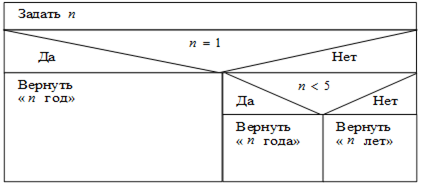
Рис. 21. Диаграмма Насси – Шнейдермана для задачи вывода грамматически верной фразы.
Графические символы, их размеры и правила построения схем алгоритмов должны выполняться в соответствии с государственным стандартом ГОСТ 19.701-90, согласно которому каждой группе действий соответствует блок особой формы.
Полный текст стандарта можно посмотреть по адресу http://vsegost.com/Catalog/28/28346.shtml. Настоящий стандарт распространяется на условные обозначения (символы) в схемах алгоритмов, программ, данных и систем, и устанавливает правила выполнения схем, используемых для отображения различных видов задач обработки данных и средств их решения.
Стандарт не распространяется на форму записей и обозначений, помещаемых внутри символов или рядом с ними и служащих для уточнения выполняемых ими функций
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов. Он занимает промежуточное место между естественным и формальным языками. С одной стороны, псевдокод близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст.
С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи. В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя.
Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций. К таким конструкциям обычно относят ветвления (если …то … иначе …) и циклы (цикл от … до …, цикл пока, цикл до. ).
Примером такого языка является алгоритмический язык, предложенный академиком А. Ершовым.
С конца 80-х годов XX века и в настоящее время при изучении информатики в советских (ныне российских) школах для изучения основ алгоритмизации применяется т. н. русский алгоритмический язык (школьный алгоритмический язык), использующий понятные школьнику слова на русском языке. Алголо-подобный алгоритмический язык с русским синтаксисом был введён в употребление академиком А. П. Ершовым в середине 1980-х годов, в качестве основы для «безмашинного» курса информатики. Впервые был опубликован в учебнике «ОИВТ» в 1985 г.
Алгоритм на школьном алгоритмическом языке в общем виде записывается в форме:
алг название алгоритма (аргумент и результат)
дано условия применимости алгоритма
надо цель выполнения алгоритма
нач описание промежуточных величин
| последовательность команд (тело алгоритма)
В записи алгоритма ключевые слова обычно подчёркивались либо выделялись полужирным шрифтом. Для выделения логических блоков применялись отступы, а парные слова начала и конца блока соединялись вертикальной чертой.
Пример алгоритма вычисления суммы квадратов на школьном алгоритмическом языке.
алг Сумма квадратов (арг цел n, рез цел S)
надо | S = 1*1 + 2*2 + 3*3 + … + n * n
| нц для i от 1 до n
| | S := S + i * i
| вывод «S = «, S
В настоящий момент язык переживает свое второе рождение, в связи с разработкой пакета «КуМир» для Windows и Linux. В системе используется несколько исполнителей — основные — это классические Робот и Чертёжник. Пакет включен в дистрибутив ALT Linux Школьный.
Система КуМир разработана в НИИСИ РАН по заказу Российской Академии Наук и распространяется свободно на условиях лицензии GNU GPL 2.0.
В последние несколько лет школьный алгоритмический язык включается как один из предлагаемых в текстах задач ЕГЭ по информатике.
При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается определенный произвол при изображении команд. Вместе с тем такая запись точна настолько, что позволяет человеку понять суть дела и исполнить алгоритм.
Однако на практике в качестве исполнителей алгоритмов используются специальные автоматы — компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на «понятном» ему языке. И здесь на первый план выдвигается необходимость точной записи команд, не оставляющей места для произвольного толкования их исполнителем.
Следовательно, язык для записи алгоритмов должен быть формализован. Такой язык принято называть языком программирования, а запись алгоритма на этом языке — программой для компьютера.
Алгоритмические конструкции
Дата добавления: 2018-09-22 ; просмотров: 691 ; Мы поможем в написании вашей работы!
Источник: studopedia.net
Словесная форма представления алгоритма
При словесной записи алгоритмы записываются в виде текста с формулами по пунктам, определяющими последовательность действий. Для записи алгоритмов используются средства обычного языка, но с тщательно отрабатывают наборы слов и фраз, не допускающие повторений, синонимов, лишних слов. Принимаются определенные соглашения о форме записи, порядке выполнения действий, допускается использование математических символов. При написании алгоритмов в словесной форме используют следующую структуру записи:
Разветвляющиеся алгоритмы:
5. Если , то перейти к пункту 6, иначе перейти к пункту 7.
6. операторы, перейти к пункту № (операторы, следующие за ветвлением)
Циклические алгоритмы:
Первый способ организации цикла (цикл с предусловием):
1. Установка начальных значений переменных, использующихся (изменяющихся) в цикле.
2. ПРОВЕРКА: продолжить цикл?
ДА выполняется тело цикла;
изменяется значение переменной цикла;
возвращаемся на проверку в пункт 2.
НЕТ выходим из цикла на пункт 3.
Второй способ организации цикла (цикл с постусловием):
1. Установка начальных значений переменных, использующихся (изменяющихся) в цикле.
2. Выполнение тела цикла.
Изменение переменной цикла.
3. ПРОВЕРКА: закончить цикл?
ДА выход из цикла на пункт 4.
НЕТ возвращаемся на пункт 2.
4. Операторы, следующие за телом цикла.
Второй способ организации цикла (цикл с параметром):
5. Для iот 1 доnперейти к пункту 6
6. Для jот 1 доnперейти к пункту 7
8. Операторы, следующие за телом цикла.
Пример 1 – алгоритм Евклида.
Задача, даны два целых положительных числа, найти их наибольший общий делитель (НОД).
Решение этой задачи может быть получено последовательным делением вначале большего числа на меньшее, затем меньшего числа на полученный остаток, первого остатка на второй остаток и т.д. до тех пор, пока в остатке не получится нуль. Последний по счету делитель и будет искомым результатом.
Обозначим через M и N исходные целые числа, приняв в качестве их начальных значений заданные константы. Сведем деление к повторному вычитанию. Тогда алгоритм может быть сформулирован следующим образом:
1. задать два числа;
2. если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;
3. определить большее из чисел;
4. заменить большее из чисел разностью большего и меньшего из чисел;
5. повторить алгоритм с шага 2.

3. Если MN, то перейти к п.4, иначе перейти к п. 7
4. Если M>N, то прейти к п. 5, иначе перейти к п. 6.
5. М: = М-N; перейти к п. 3.
6. N: = N-М; перейти к п. 3.
Словесный способ не имеет широкого распространения по следующим причинам:
- такие описания строго не формализуемы;
- страдают многословностью записей;
- допускают неоднозначность толкования отдельных предписаний.
Графический способ записи алгоритмов
Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Внутри блока дается описание соответствующего действия.
Такое графическое представление называется схемой алгоритма или блок-схемой. Графическое изображение алгоритма широко используется перед программированием задачи вследствие его наглядности,т.к. зрительное восприятие обычно облегчает процесс написания программы, ее корректировки при возможных ошибках, осмысливание процесса обработки информации.
Можно встретить даже такое утверждение: “Внешне алгоритм представляет собой схему – набор прямоугольников и других символов, внутри которых записывается, что вычисляется, что вводится в машину и что выдается на печать и другие средства отображения информации“. Здесь форма представления алгоритма смешивается с самим алгоритмом.
Принциппрограммирования “сверху вниз”требует, чтобы блок-схема поэтапно конкретизировалась и каждый блок “расписывался” до элементарных операций. Но такой подход можно осуществить при решении несложных задач. При решении сколько-нибудь серьезной задачи блок-схема “расползется” до такой степени, что ее невозможно будет охватить одним взглядом.
Блок-схемы алгоритмов удобно использовать для объяснения работы уже готового алгоритма, при этом в качестве блоков берутся действительно блоки алгоритма, работа которых не требует пояснений. Блок-схема алгоритма должна служить для упрощения изображения алгоритма, а не для усложнения.
При решении задач на компьютере необходимо не столько умение составлять алгоритмы, сколько знание методов решения задач (как и вообще в математике). Поэтому изучать нужно не программирование как таковое (и не алгоритмизацию), а методы решения математических задач на компьютере.
Задачи следует классифицировать не по типам данных, как это обычно делается (задачи на массивы, на символьные переменные и т. д.), а по разделу “Требуется”. Схема- это графическое представление алгоритма, дополненное элементами словесной записи.
Каждый пункт алгоритма отображается на схеме некоторой геометрической фигурой-блоком (блочным символом), причем различным по типу выполняемых действий блокам соответствуют различные геометрические фигуры. Графические символы на схеме соединяются линиями потока информации.
Основное направление потока информации идет сверху вниз и слева на право (стрелки на линиях могут не указываться). В других случаях применение стрелок обязательно. По отношению к блоку линии потока могут быть входящимииливыходящими. Количество входящих линий для блока принципиально не ограничено. Выходящая линия может быть только одна.
Исключение оставляют логические блоки, имеющие не менее двух выходящих линий потока, каждая из которых соответствует одному из возможных исходов проверки логического условия, а также блоки модификации. Блок вычислительный процессприменяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Таблица 1. Условные графические обозначения, применяемые при составлении схем алгоритмов.
| № п/п | Назва-ние символа | Сим-вол | Отображаемая функция |
| 1 | Блок вычислений |  |
Вычислительное действие или последовательность вычислительных действий |
| 2 | Логический блок |  |
Выбор направления выполнения алгоритма в зависимости от некоторых условий |
| 3 | Блоки ввода – вывода |  |
Общее обозначение ввода или вывода данных |
 |
Вывод данных, носителем которых служит документ | ||
| 4 | Начало-конец |  |
Начало или конец программы, останов, вход или выход в подпрограммах |
| 5 | Предоп-ределен-ный процесс |  |
Вычисления по стандартной подпрограмме или подпрограмме пользователя |
| 6 | Блок модифи-кации |  |
Выполнение действий, изменяющих пункты алгоритма |
| 7 | Соединитель |  |
Указание связи между прерванными линиями потока информации в пределах одной страницы |
| 8 | Межстраничный соедини-тель |  |
Указание связи между частями схемы, расположенными на разных листах |
| 9 | Магнит-ный диск |  |
Ввод-вывод данных, носителем которых служит магнитный диск |
| 10 | Коммен-тарий |  |
Связь между элементами схемы и пояснением |
Логический блокиспользуется для обозначения переходов управления по условию. В каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок предопределенный процессиспользуется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам. Блок модификацияиспользуется для организации циклических конструкций.
Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения. При большом количестве пересекающихся линий, большой их длине и многократных изменениях направления схемы становится малонаглядной.
В этих случаях допускается разрывать линии потока информации, размещая на обоих концах разрыва специальный символ «соединитель» (рис. 1). Внутри поля соединителей, отмечающих разрыв одной и той же линии, ставится одинаковая маркировка отдельной буквой или буквенно-цифровой координатой блока, к которому подходит линия потока.  Рис.
Рис.
1. Соединитель Если схема располагается на нескольких листах, переход линий потока с одного листа на другой обозначается с помощью символа «межстраничный соединитель» (рис 2). При этом на листе с блоком – источником соединитель содержит номер листа и координаты блока-приемника, а на листе с блоком–приемником – номер листа и координаты блока – источника.
 Рис. 2. Межстраничный соединитель Внутри блоков и рядом с ними делают записи и обозначения (для уточнения выполняемых ими функций) так, чтобы их можно было читать слева направо и сверху вниз независимо от направления потока. Например, на рис. 3 вид 1 и вид 2 читаются идентично.
Рис. 2. Межстраничный соединитель Внутри блоков и рядом с ними делают записи и обозначения (для уточнения выполняемых ими функций) так, чтобы их можно было читать слева направо и сверху вниз независимо от направления потока. Например, на рис. 3 вид 1 и вид 2 читаются идентично. 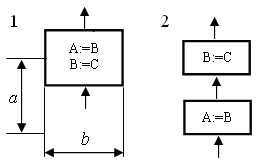 Рис.
Рис.
3. Порядковые номера блоков проставляют в верхней части графического символа в разрыве его контура (рис. 1 и 4).  Рис. 4 При выполнении схем алгоритмов необходимо выдерживать минимальное расстояние 3 мм между параллельными линиями потоков и 5 мм между остальными символами.
Рис. 4 При выполнении схем алгоритмов необходимо выдерживать минимальное расстояние 3 мм между параллельными линиями потоков и 5 мм между остальными символами.
В блоках приняты размеры:  =10, 15, 20 мм;
=10, 15, 20 мм; =1.5
=1.5 (рис.3). Если необходимо увеличить размер схемы, то допускается увеличивать
(рис.3). Если необходимо увеличить размер схемы, то допускается увеличивать на число кратное пяти.
на число кратное пяти.
Схема является исключительно наглядным и простым способом представления алгоритма. При этом не накладывается никаких ограничений на степень детализации в изображении алгоритма. Выбор ее целиком зависит от программиста. Но, нужно иметь ввиду, что излишне общий характер схемы нежелателен из-за малой информативности, а очень детальная схема проигрывает в наглядности.
Для особенно сложных и больших алгоритмов, целесообразно составлять несколько схем различных уровней детализации. Схема 1-го уровня отображает весь алгоритм целиком. Схемы 2-го уровня раскрывают логику отдельных блоков схемы 1-го уровня. При необходимости могут быть составлены схемы последующих уровней с еще большей степенью детализации. Такое пошаговое уточнение схемы алгоритма составляет сущность метода нисходящего проектирования, который, в свою очередь, является основой структурного программирования.
Источник: studfile.net
Способы представления алгоритмов

1. Словесный. Такое описание алгоритма состоит из словесного перечня действий в виде предложений.
Например, вычислить C=
Исходные данные А и В ввести в память ЭВМ, проверить выполнение неравенства АB. Если оно выполняется, то вычислить А-В. Результат обозначить как С и вывести его; в противном случае вычислить А+В, результат обозначить С и вывести его.
Недостаток такого представления — отсутствие четкой формализации и наглядности выполнения процесса.
Достоинством является то, что таким способом можно описывать алгоритмы с любою степенью детализации.
2. Формульно-словесный способ основан на задании инструкций о выполнении конкретных действий в четкой последовательности в сочетании со словесными пояснениями.
Для рассмотренного задания алгоритм, представленный формульно-словесным способом, будет следующим:
Этап 1. Ввести А, В.
Этап 2. Если АB, то перейти к этапу 4, иначе — к этапу 3.
Этап 3. С=А-В, перейти к этапу 5.
Этап 5. Принять значение С за результат.
Этап 6. Вывести С.
Этот способ более компактен, но не является строго формальным.
3. Табличный. Алгоритм задается в виде таблиц и расчетных форм. Этот способ наиболее часто используется в экономических расчетах. Исходные данные и результаты вносятся в заголовки столбцов таблицы.
4. Операторный (язык операторных схем). При использовании этого способа вычислительный процесс изображается в виде последовательности символов (операторов). Они обозначают группы стандартных или нестандартных операций, реализующих законченную процедуру с указанием связи между отдельными операторами. Этот способ значительно упрощает составление программы для компьютера, при этом вместо операторов подставляются соответствующие команды. Недостатком данного способа является его малая наглядность.
5. Графический (способ блок-схем). При таком представлении алгоритма каждый этап отображается в виде геометрических фигур — “блоков”, форма которых зависит от выполняемой операции. Блок может иметь имя (метку). Линия соединения блоков показывает направление процесса обработки данных. Каждое направление называется ветвью.
Перечень блоков, их наименование, функции, формы, размеры определяются ГОСТ 19.003- 80.
Указанный ГОСТ регламентирует изображение и размеры отдельных блоков в блок-схеме, а также их взаимное расположение. Блоки, в которых не предусматривается разветвление алгоритма по условию, имеют вид прямоугольника с размерами сторон, отношение которых равно 3:2.
Блоки, предусматривающие проверку условия с последующим разветвлением, — форму ромба, соотношение диагоналей которого также равно 3:2. Каждая блок-схема обязательно должна включать в себя блок-начало и блок-конец. Форма этих блоков — прямоугольник со скругленными углами, размеры — 3:1. Отдельно определяются блоки, в которых осуществляется ввод и вывод информации.
В зависимости от того, откуда и куда осуществляется ввод/вывод, используются разные виды блоков ввода/вывода. Однако можно использовать блок ввода/вывода общего назначения в виде параллелограмма с соотношением длины основания к высоте как 3:2. Блоки соединяются стрелками, показывающими последовательность исполнения. Сам значок “стрелка” в направлении “вниз” и “вправо” можно не ставить, “вверх” и “влево ” — ставить обязательно. Блоки должны быть расположены так, чтобы расстояние между блоками и стрелками составляло не меньше 5 мм.
Алгоритм линейной структуры состоит из последовательности действий, формирующих одну ветвь вычислений. Примером линейного алгоритма может быть алгоритм расчета У по формуле У=Х 2 .
Решение задач не всегда можно представить в виде линейного алгоритма. Существуют задачи, в которых требуется организовать выбор выполнения последовательности действий в зависимости от каких-либо условий. Такие алгоритмы называются алгоритмами разветвляющейся структуры. В них должен присутствовать один или несколько логических операторов (проверки условия) и несколько ветвей решения. Примером разветвляющегося алгоритма может быть выбор наибольшего из двух введенных произвольных чисел.
Алгоритмы, отдельные действия в которых многократно повторяются, называются алгоритмами циклической структуры. Совокупность повторяющихся действий алгоритма принято называть циклом. При разработке циклического алгоритма вводят следующие понятия: параметр цикла — величина, с изменением значения которой связано многократное выполнение цикла; начальное и конечное значение параметров цикла; шаг цикла — значение, на которое изменяется параметр цикла при каждом повторении.
Цикл организуют по определенным правилам. Циклический алгоритм состоит из подготовки цикла; тела цикла; условия продолжения цикла.
В подготовку цикла входят действия, связанные с заданием исходных данных для параметров цикла и других величин, использующихся в цикле.
В тело цикла входят многократно повторяющиеся действия для вычисления искомых величин; подготовка следующего значения параметра цикла, подготовка других значений, необходимых для повторного выполнения действий в теле цикла.
В условии продолжения цикла определяется необходимость дальнейшего выполнения повторяющихся действий (тела цикла). Если параметр цикла превысил конечное значение, то выполнение цикла должно быть прекращено.
Примером циклического алгоритма выступает алгоритм определения суммы десяти произвольных чисел, вводимых пользователем.
Статьи к прочтению:
- Способы совместного использования шин системного интерфейса процессором и контроллером пдп
- Способы защиты от троянских программ
ОАиП. Лекция 1
Похожие статьи:
- Алгоритм. способы записи алгоритмов Для того чтобы ЭВМ выполнила некоторые действия необходимо задать последовательность инструкций (команд) на понятном компьютеру…
- Способы описания алгоритмов Существуют несколько способов описания алгоритма: словесное, псевдокод, блок-схема, программа. Словесное описание представляет структуру алгоритма на…
Источник: csaa.ru