Приведем пример модуля Lib, содержащего описание типа и две функции для вычисления расстояния между двумя точками на плоскости и площади треугольника, и программы, использующей этот модуль.
Листинг модуля Lib.pas
Interface
Tdot=Record
x,y:Real;//координаты точки x и y
Function Distance(d1,d2:Tdot):real; // расстояние между точками d1 и d2
FunctionSquareT(d1,d2,d3:Tdot):real; // площадь треугольника, заданного 3-мя точками
Implementation
Function Distance(d1,d2:Tdot):real;
FunctionSquareT(d1,d2,d3:Tdot):real;
var a, b, c, p : Real;
a:=Distance(d1,d2);// находим расстояние между точками d1 и d2
b:=Distance(d2,d3); // находим расстояние между точками d2 и d3
c:=Distance(d3,d1); // находим расстояние между точками d3 и d1
Result := Sqrt(p * ( p – a ) * ( p – b ) * ( p – c ) );
Листинг программы TesLib, использующей модуль Lib.pas
program TestLib;
Lib; // подключение модулей SysUtils и Lib
Расстояние между двумя точками (прямоугольная система координат на плоскости).
var a, b, c : Tdot;
write(‘Введите координаты X иY1-й вершины треугольника -’);
write(‘Введите координаты X иY2-й вершины треугольника -’);
write(‘Введите координаты X иY3-й вершины треугольника -’);
s := SquareT(a, b, c);
writeln(‘Площадь треугольника = ’,s:6:2);
p:= Distance(a, b)+ Distance(b, c)+ Distance(c, a);
writeln(‘Периметр треугольника = ’,p:6:2);
Пример модуля, реализующего стек с целыми числами.
Приведем пример модуля Steck, который содержит минимальный набор процедур и функций для работы со стеком и сами данные. Стек можно организовать на основе массива из целых чиселM. Для контроля над заполнением массива новыми значениями введем целочисленную переменнуюtop, которая всегда будет хранить номер свободной ячейки массива.
Причем данные опишем в исполнительной части массива, исключив прямое обращения к ним из программы, использующей модуль. Обращаться к ним будем только с помощью процедур и функций.
Таким скрытием данных можно дополнительно гарантировать корректность работы пользователя со стеком (при прямом неправильном изменении переменнойtopможно потерять некоторые данные из стека, например операторtop:=0 очистит весь стек). Пользователям, подключающим модуль необходимо предоставить методы для работы со стеком: поместить число в стек, извлечь число из стека, проверить стек на пустоту и т.д.
Эти процедуры и функции необходимо поместить в интерфейсную часть модуля. Так как, структура хранения данных стека не доступна из программы, то физическая реализация стека может быть совершено различной: динамический массив, связный список. Но программы, которые будут использовать этот модуль не должны изменяться при изменении реализации стека. Они будут пользоваться одним и тем же набором процедур и функций, описанных в интерфейсной части. То есть при изменении способа реализации стека интерфейсная часть модуля остается неизменной, а меняется текст и данные в исполнительной части.
Расстояние между двумя точками. Координаты середины отрезка.
Структура стека на базе массива изображена на рис.1. Новый элемент будет добавляться на место с номером top, после этогоtopнеобходимо увеличить на единицу. При извлечении элемента из стекаtopуменьшается на единицу и из этой позиции извлекается очередное число. Теперь эта позиция считается пустой.
Стек пустой – если значениеtopравно 0. Для инициализации стека (его очистки) достаточно переменнойtop присвоить 0. В программе извлечение числа из пустого стека приведет к ошибке, поэтому перед такой операцией пользователь должен убедиться, что в стеке есть элементы. Стек организуем на базе динамического массива. Его размер можно увеличивать по мере заполнения стека новыми значениями. Массив окажется полностью заполненным, если число элементов совпадет сtop. Это необходимо проверять перед добавлением нового элемента.
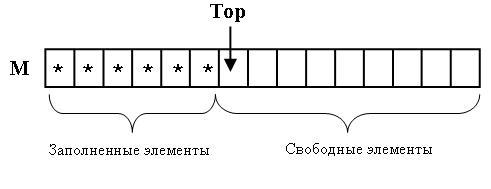
Рис.1 Структура стека на базе массива
Листинг модуля Steck.
Источник: studfile.net
Программа вычисления расстояния между двумя точками плоскости
Вопрос по информатике:
Паскаль (9 класс!) Напишите программу вычисления расстояния между двумя точками плоскости
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
- bookmark_border
- 17.07.2017 21:24
- Информатика
- remove_red_eye 7053
- thumb_up 79
Ответы и объяснения 1
xcathorans
Program Distance;
Var
X1, Y1, X2, Y2, D: Real;
Begin
WriteLn(‘Введите координаты первой точки’);
ReadLn(X1, Y1);
WriteLn(‘Введите координаты второй точки’);
ReadLn(X2, Y2);
D := Sqrt(Sqr(X2 — X1) + Sqr(Y2 — Y1));
WriteLn(‘Расстояние между точками = ‘, D:2:2);
ReadLn;
End.
- 17.07.2017 23:24
- thumb_up 27
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Информатика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Информатика — наука о методах и процессах сбора, хранения, обработки, передачи, анализа и оценки информации с применением компьютерных технологий, обеспечивающих возможность её использования для принятия решений.
Источник: online-otvet.ru
Javascript: вычисление расстояния между двумя точками на поверхности Земли

Учитывая положение X и Y на плоскости, расстояние между двумя точками можно вычислить, используя теорему Пифагора.
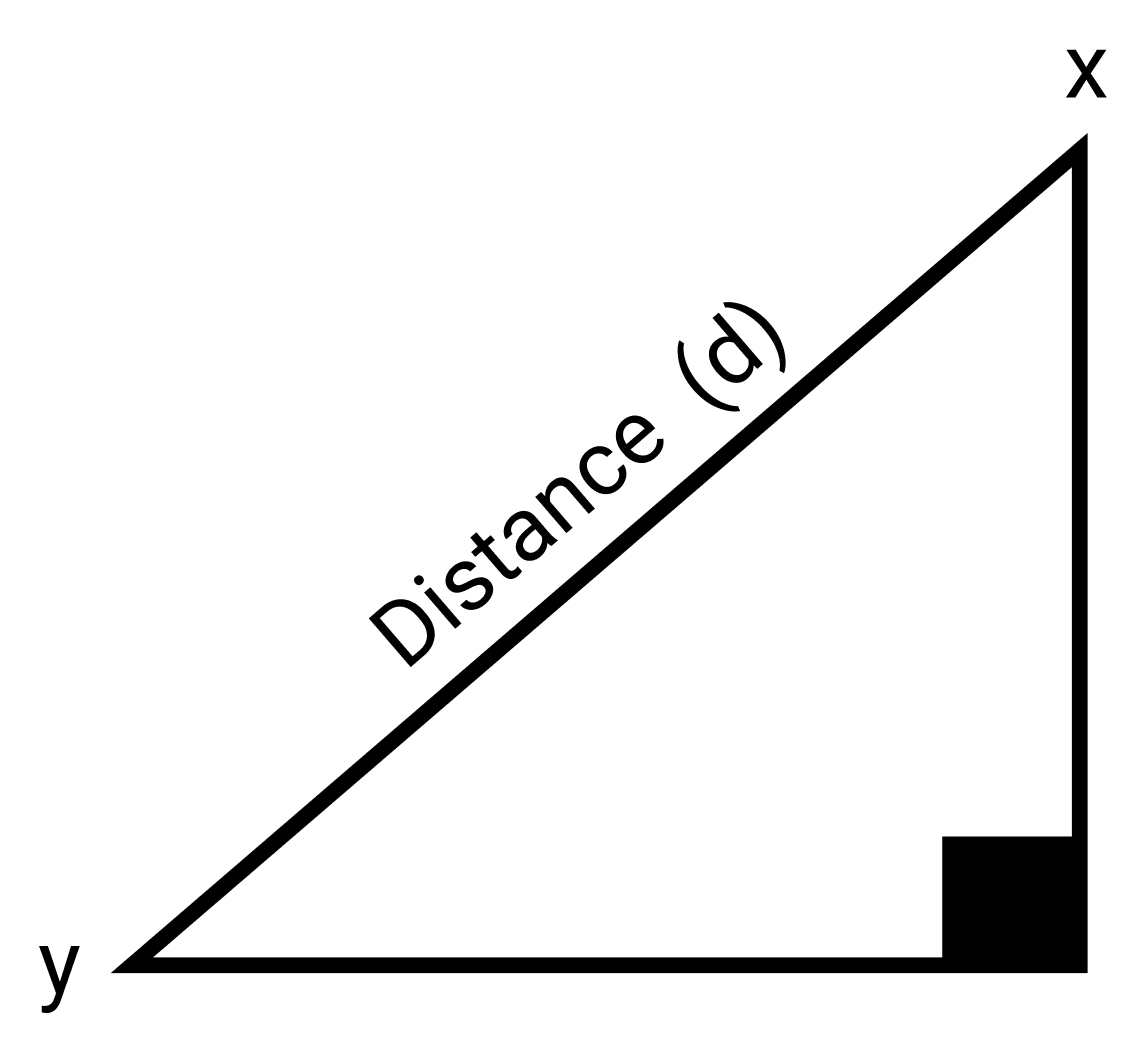
Уравнение для которой выглядит так:
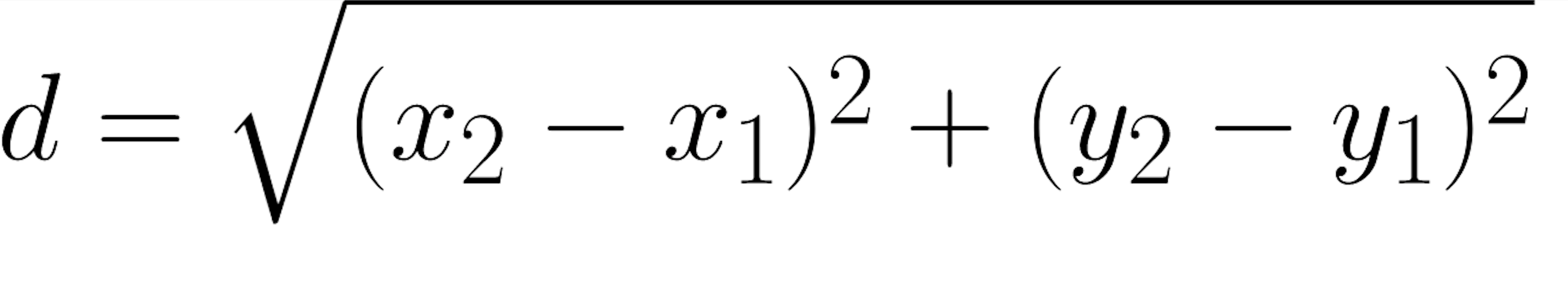
Теперь это можно преобразовать в код:
Во-первых, javascript предоставляет объект Math , который является основной утилитарной библиотекой. Начнём из внутренностей уравнения:
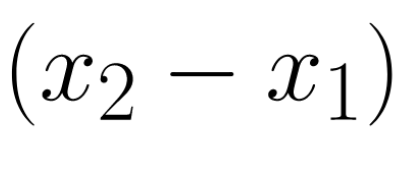
Здесь на самом деле понадобится расчёт абсолютной величины разности, например:
Math.abs(20–5) = 15 или Math.abs(5-20) = 15
Затем, результат нужно возвести в квадрат с помощью функции Math.pow() :
Math.pow(result, 2);
Полученное для x и y надо сложить и получить квадратный корень с помощью Math.sqrt() . Полное уравнение в Javascript будет выглядеть следующим образом:
Math.sqrt(Math.pow(Math.abs(x1 — x2)) + Math.pow(Math.abs(y1 — y2)));
Этого будет достаточно для плоскости, но результат будет совершенно неточным при вычислении расстояния для поверхность Земли, которая по сути является сферой (сплюснутый сфероид).
Расстояние на поверхности сферы
Чтобы рассчитать точнее, потребуются два дополнительных уравнения.
Во-первых, понадобится способ вычисления угла между двумя точками от центра сферы, за которым последует уравнение для вычисления расстояния между двумя точками с учетом центрального угла (результат предыдущего уравнения). Используем математические формулы, чтобы реализовать оба. Начнем с вычисления угла между двумя точками от центра.
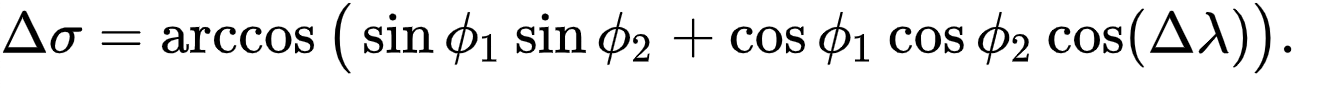
- Δ (delta) представляет разницу
- σ – центральный угол, который надо вычислить
- arcos или обратный косинус (cos в степени -1) в Javascript представлен Math.acos()
- Φ значение широты
- λ значение долготы
Преобразуем это уравнение в код. Но, прежде чем приступим, следует обратить внимание, что придётся иметь дело с радианами, а не с градусами, поскольку это гораздо более точный способ измерения углов, и что более важно, тригонометрия Javascript работает не в градусах, а в радианах.
Для реализации преобразования понадобятся следующие функции:
const degreesToRadians = degrees => degrees * (Math.PI / 180); const radiansToDegrees = radians => radians * (180 / Math.PI);
Затем все, что останется сделать, это поместить оставшуюся часть уравнения в функцию, использующую тригонометрические утилиты Javascript Math. Функция будет выглядеть примерно так:
const centralSubtendedAngle = (locationX, locationY) =>
Следующее, что нужно будет рассчитать, – это расстояние до дуги centralSubtendedAngle . Это можно описать следующим образом:
2 * PI * * ( / 360);
Земля, как полагают, имеет радиус 6371 км. Используем это в Javascript-коде:
const earthRadius = 6371 const greatCircleDistance = angle => 2 * Math.PI * earthRadius * (angle / 360); const distanceBetweenLocations = (locationX, locationY) => greatCircleDistance(centralSubtendedAngle(locationX, locationY));
Вызов distanceBetweenLocations выглядит следующим образом:
const NewYork = ; const Sydney = ; console.log(distanceBetweenLocations(NewYork, Sydney));
Последнее замечание: из-за искажений на поверхности Земли этот метод не будет точным на 100%, однако точность будет примерно 0,05% и это достаточно хороший результат.
Источник: xhtml.ru