Например, нужно вычислить площадь круглой колонны. Диаметр не измеришь. Какие формулы использовать, чтобы высчитать её площадь.
комментировать
в избранное
7 лет назад
S = П*r²
Формула длины окружности (периметра):
P = 2*П*r
П — это число Пи: 3.14.
Из окружности находим радиус:
r = P/2П
И подставляем это в формулу площади:
S = П*(P/2П)² = П*P²/4П²
Если я правильно раскрыл скобки со степенями, то:
П — сокращаются и остаётся:
S = P²/4П
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное ссылка отблагодарить
Ксарф акс [156K]
6 лет назад
Для того, чтобы найти площадь круга через длину окружности, нужно сначала вспомнить формулы, по которым вычисляется:
1) Длина окружности.
2) Площадь круга.
Итак, формула для длины окружности:
l =2πR.
Что касается площади круга, то она вычисляется по формуле:
C = πR².
Здесь R — это радиус, а π — число Пи, которое равно 3,14.
Длина окружности. Площадь круга — математика 6 класс
Если известна длина окружности, то легко выразить её радиус. После этого остаётся лишь подставить полученное значение в формулу для площади круга.
C = π * (l / 2π)² = l² / 4π.
Пример
Дана длина окружности l = 20 см. Нужно найти площадь круга.
C = l² / 4π = (20 * 20) / (4 * 3,14) = 400 / 12,56 = 31,85 см.
Таким образом, если длина окружности равна 20 см., то площадь круга будет составлять 31,85 см.
комментировать
в избранное ссылка отблагодарить
Урани я [161K]
2 года назад
Площадь круга можно легко рассчитать по известной формуле, в которую входит радиус круга (или окружности, что одно и то же):
S = πR²;
Где R – это радиус окружности, а число π – это неизменяемая величина, равная — 3,14
В свою очередь, длина окружности тоже рассчитывается через его радиус:
С = 2πR;
Отсюда следует, что выразив радиус окружности из последней формулы (R = C/2π) , и подставив его в первую формулу, мы получим формулу, в которой площадь круга будет выражена через его длину окружности:
S = π(C/ 2π)².
После возведения в квадрат и необходимых сокращений, получим окончательную искомую формулу:
S = C²/4π
Эта именно та формула, в которой площадь (S) круга выражена через его длину окружности (С).
Источник: www.bolshoyvopros.ru
Программа вычисления площади круга если известна длина окружности

Опубликовано 22.08.2017 по предмету Информатика от Гость >> Оцени ответ


- Алгебра

- Математика

- Русский язык

- Українська мова

- Информатика

- Геометрия

- Химия

- Физика

- Экономика

- Право

- Английский язык

- География

- Биология

- Другие предметы

- Обществознание

- История

- Литература

- Українська література

- Беларуская мова

- Қазақ тiлi

Показать ещё
КАК НАЙТИ ПЛОЩАДЬ КРУГА, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 класс
Источник: www.shkolniku.com
Задача: определить площадь круга, если известна длина окружности
Длина окружности 5 м. Найти площадь круга, ограниченного этой окружностью.
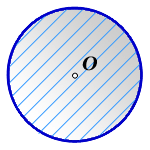
Дано:
Длина окружности, L = 5 м
Пояснение к рисунку:
O — центр окружности
Найти площадь круга: S
Используем формулу площади круга через радиус. Но нам пока не известен радиус, его надо найти.
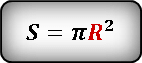
Определить радиус, нам поможет формула длины окружности.
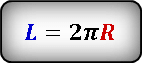
После преобразования, выразим радиус через длину окружности и подставим значения.
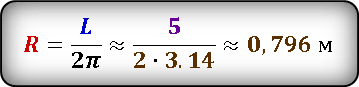
![]()
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Получили значение радиуса окружности.

В формулу площади круга, подставляем найденное значение радиуса.
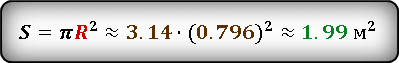
Ответ:

Если в формулу площади круга подставить выраженный радиус через длину окружности, то получим следующую формулу, в которой площадь круга сразу выражена через длину окружности. Проверим, подставив наше значение
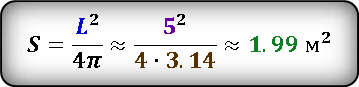
Калькулятор для расчета площади круга
![]()
Источник: www-formula.ru