Программа вычисления функции при заданных значениях аргументов

Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок «Что такое функция в математике».

После того, как вы действительно поймете, что такое функция (возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.

В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.

Как получить значение функции

Рассмотрим задание. Функция задана формулой « y = 2x − 1 »

1. Вычислить « y » при « x = 15 »
2. Найти значение « x », при котором значение « y » равно « −19 ».

Для того, чтобы вычислить « y » при « x = 15 » достаточно подставить в функцию вместо « x » необходимое числовое значение.

Запись решения выглядит следующим образом.

y(15) = 2 · 15 − 1 = 30 − 1 = 29

Для того, чтобы найти « x » по известному « y », необходимо подставить вместо « y » в формулу функции числовое значение.

То есть теперь наоборот, для поиска « x » мы подставляем в функцию « y = 2x − 1 » вместо « y » число « −19 » .

Передача параметров в функцию по значению. Параметры функции. Передача аргументов в функцию. #34

Программа вычисления функции для заданных значений аргументов с использованием рядов

Составить программу вычисления функции для заданных значений аргумен-тов с использованием рядов. Суммы рядов вычислить с погрешностью e.

В программе предусмотреть защиту от зацикливания итерационного процесса, подсчет и вывод на печать числа итераций, за которое удается найти сумму ряда с заданной погрешностью. Для проверки программы вывести на печать значения функций f1 и f2, вычисленные с помощью рядов и соответствующих им аналитических зависимостей.

1- x 2 /2!+. +(-1) n* x 2n /(2n)!+

-1/2ln(1-2xcos p/3+x 2

Погрешность: 10 -3

Теоретическая часть

При вычислении значения функции с использованием функционального ряда

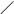
fn (x) = f1(x) + f2(x) + . + fn(x) + . , (1)

n=1

задача сводится к последовательному вычислению частичных сумм S1(x), S2(x), . , Sn(x). , где

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnline

Sn(x) = fi (x).

Для сходящегося ряда существует предел

lim Sn(x) = S(x), где S(x) — сумма функционального ряда. При вычислении суммы равномерно сходящегося ряда с заданной погрешностью E в качестве окончательного результата принимается значение частичной суммы Sn (x), для которой выполняется условие

т.е. абсолютная величина очередного слагаемого не превышает значения E.

В общем случае начальное значение номера члена ряда в формуле (1) может быть отличным от единицы (например, равным нулю). Обозначив его через k, получим

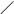
S(x) = f n(x). (3)

Процесс вычисления суммы ряда (1) определяется рекуррентным соотношением

суммирование считается законченным при выполнении условия достижения заданной точности (2). Начальное значение суммы принимается равным нулю. Алгоритм вычисления суммы функционального ряда приведен на рис. 1.

В схеме алгоритма на рис. 1 и последующих алгоритмах данной темы входными параметрами для алгоритма вычисления суммы ряда являются значения x и e (блок 1), выходными — значение суммы S (блок 7). Переменная f представляет собой значение очередного члена ряда. Поскольку в вычислениях по рекуррентной формуле (3) одновременно участвуют лишь два значения: Sn-1(x) и Sn (x), в схеме алгоритма для их обозначения используется одна переменная S (блок 4). Значение S изменяется при прибавлении очередного члена суммы: справа от знака присваивания значение переменной S соответствует предыдущему значению суммы Sn-1 (x), слева — текущему Sn(x).

При составлении алгоритма вычисления суммы конкретного ряда в блоке (3) параметр k заменяется значением номера начального члена этого ряда, в блоке 4 величина fn(x) — формулой общего члена данного ряда.

1

Вход (x,e)

S=0

3

n=k

4

5

n=n+1

6

— f > e

7 +

Выход (S)

Обычно формула общего члена ряда принадлежит к одному из следующих типов:

а) cos nx / n; sin(2n-1)x / 2n-1; cos 2nx / 4n 2 — 1;

б) x n / n!; (-1) n x 2n+1 / (2n+1); x 2n / (2n)!;

в) n 2 +1 / n! (x / 2) n ; (-1) n cos nx / n 2 ; x 4n+1 / 4n+1.

В случае “а” вычисления будут наиболее эффективными, если каждый член ряда вычислять по его общей формуле. Вычисление суммы ряда в этом случае организуется по схеме, приведенной на рис. 1.

В случае “б” в формулу общего члена ряда входят целые степени и факториалы. Для вычисления fn (x) при этом целесообразно использовать рекуррентные соотношения, т.е. вычислять последующий член ряда через предыдущий. Это позволяет существенно сократить объем вычислений. Кроме того, непосредственное вычисление члена ряда по общей формуле в ряде случаев невозможно, например, из-за наличия факториала. Очередной член ряда можно определить через предыдущий следующим образом:

Похожие материалы

• Запросы — в центре внимания рынок сбыта. Конструирование запросов. Режимы представления запроса
• Отработка ассемблером ошибочных ситуаций. Команды управления процессом ассемблирования
• Архивирование данных. Назначение программ-архиваторов. Резервирование данных

Источник: vunivere.ru

Лабораторная работа №2 Вычисление значения функции, заданной различными аналитическими выражениями, при заданных значениях аргумента (разветвляющийся алгоритм)

Для программирования разветвляющегося алгоритма используется оператор условного перехода. Его общий вид:

If логическое выражение then оператор_1

[else оператор_2];

Квадратные скобки означают, что конструкция else оператор_2 может отсутствовать. Если логическое_выражение истинно, то выполняется оператор_1, иначе – оператор_2 (или следующий за if оператор, если else отсутствует).

Пример. Вычислим значение функции

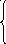
sinx, если xa,

y(x)= cosx, если axb,

Указанное выражение может быть запрограммировано в виде

if x>=b then y:=sin(x)/cos(x);

else y:=sin(x)/cos(x); .

2. Варианты заданий

Значения x (по одному значению для каждого промежутка) задать самостоятельно.

1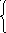) ab-x 3 , если axb, 2) 7(b/x-a/b) 2 , если xa,

y(x)= 4(x 2 +a), если xb, y(x)= 2(a-b) 3 (ax+bc), если xa,

x 2 (a+b), если xa; 3abx, если xa;

a=-0.0000124; b=2/5; a=2; b=3.5; c=4.1;

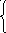
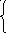3) cos(ax 2 +b) 2 , если -19x-16,

2xd+a 2 , если x-19;

4) a 2 b/9-x, если x-2,

y(x)= 4(a 3 x 2 -c 2 ), если -2x4,

tg(a-b) 2 +x 2 , если x4;

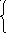
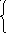5) 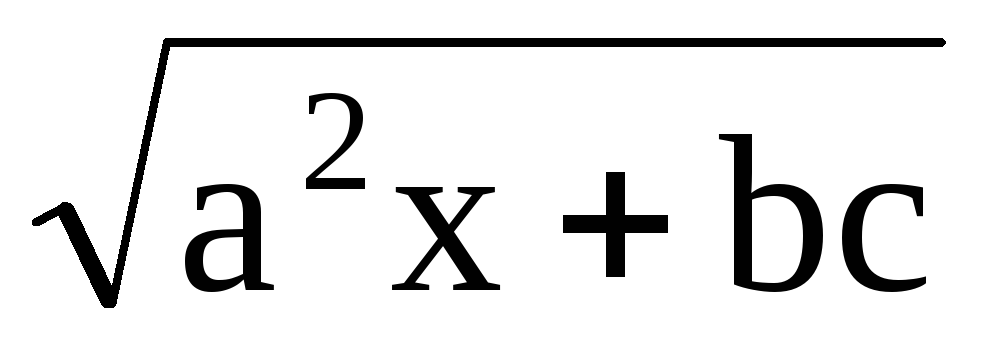, если -1xa,

y(x)= 10(ax+bx), если xa,

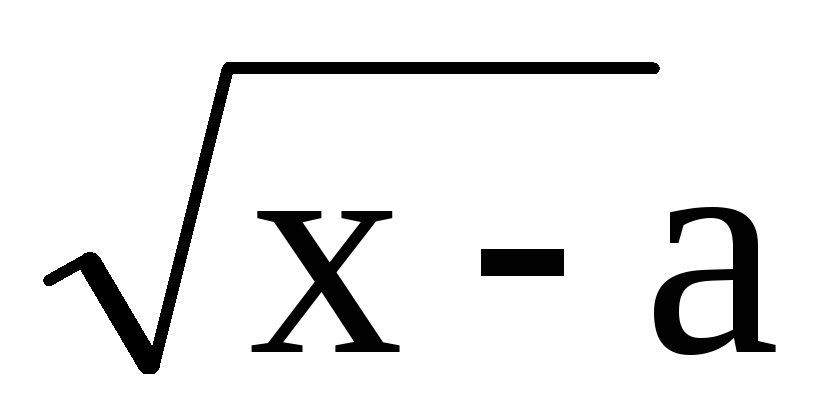
y(x)= , если -1x1,

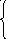
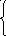
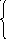
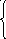7) 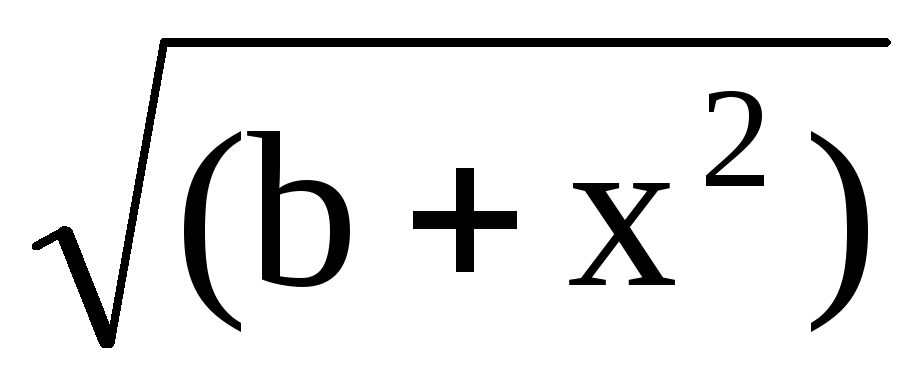, если -2x3,

y(x)= ab/x-x 2 , если x3,

8) 5b-a/(b-c)x 2 , если 3x5,

10 2 dbc/x, если x5;

9) 5c 2 d 2 b, если x3.5,

y(x)= 4(cd 2 +x 2 ), если 1.5x3.5,

(ax+b) 2 , если x3.5;

10) 4(x/a 2 -a), если x-1,

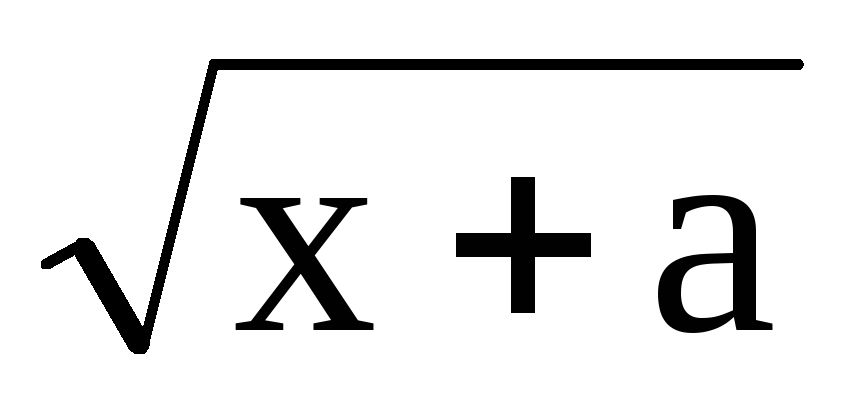
y(x)= , если -1x1,

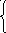
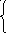
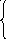11) x 2 +cos(a+bx), если x0,

(x+2)+0.0024, если 0x1;

12) (a 2 -0.008b 2 )/x, если axb,

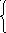
13) 0.003a/x, если xc,

y(x)= 2x/a, если xa+b,

c(ax+b) 2 , если cxa+b;

14) ab-x 2 , если x0,

y(x)= a 2 x+b 2 , если 0x0.1,

b(x 2 -a 2 ), если x0.1;

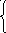
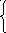15) a 3 +dx 2 , если 0.1xa,

y(x)= (b-x) 2 , если xa,

(b 2 +x 2 )a-x, если x0.1;

16) x 2 +a, если xa,

y(x)= 8.4(x+a), если axd,

dx/15-a x , если xd;

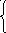
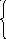17) e ax , если x-1,

y(x)= cosx+0.0085, если -1x0,

18) (ax 2 +2)/(x 2 +1), если 1x3,

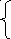
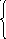19) (a-b)/(ab+x)/c, если 3x5,

y(x)= (a-b) 2 x 3 , если 5x9.8,

(ax 2 +b)/4x, если x9.8;

20) 4[ax-6(a+b) 3 ], если a+bxa,

y(x)= a 2 +(a-b)+x 2 , если xa,

x 2 (a+b), если xa+b;

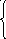
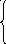21) a 2 (a-b)x, если axb,

y(x)= 5(ax 2 +b), если xb,

22) (ab-cx)/abcx 2 , если x0,

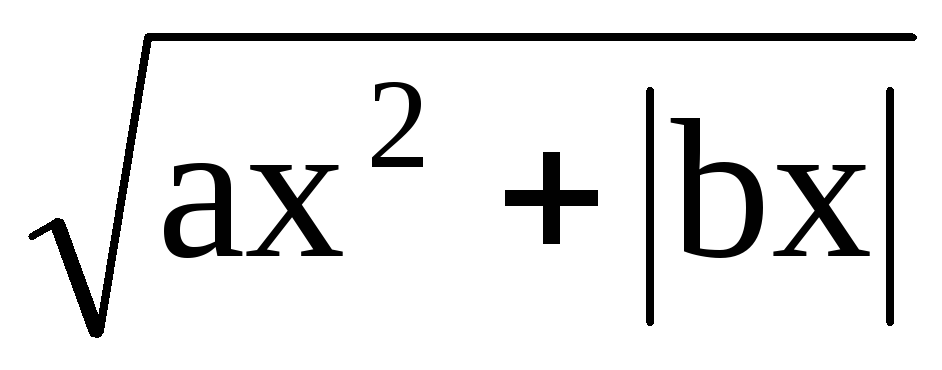
y(x)= , если 0x0.83,

x 2 +ab, если x0.83;

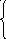
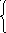23) cos(x 3 -ab-a 1/2 ), если axb,

y(x)= (x-a) 3 +b 2 , если xa,

(c+d) 2 +cx, если xb;

a=0.24; b=2; c=8/3; d=0.5;

24) 9.25-ac+dx, если axd,

y(x)= 4(d 2 /a+c 2 x/b 2 ), если xd,

ad 2 cx, если xa;

25) cos(ax+z), если axz,

y(x)= x+z+4.28, если xa,

Источник: studfile.net