Циклы применяются для решения самых разнообразных задач:
— определения экстремумов функций;
— вычисления сумм конечных и бесконечных рядов;
— вычисления определенных интегралов;
— решения алгебраических и трансцендентных уравнений численными методами;
— операций с матрицами;
— автоматизированный ввод и вывод данных.
Редкая вычислительная процедура обходится без использования циклов.
Под табулированием понимают конструирование или вычисление (составление) различных математических таблиц.
Наиболее широко этот метод использовался до появления вычислительной техники. Например, для вычисления значений тригонометрических функций, интегралов широко использовались таблицы, рассчитанные в научных центрах и представленные в виде таблиц. Табличные методы задания функций могут применяться и в малых вычислительных машинах для сокращения времени вычисления с использованием методов интерполяции и экономии памяти, необходимой для хранения сложных программ вычисления по точным формулам. Табулирование может применяться также для построения графиков функций.
Табулирование функции в Pascal 9 класс
Суть табулирования функции состоит в том, что весь диапазон изменения независимой переменной разбивают на равные интервалы и для каждого значения аргумента в граничных точках интервалов (узлах интерполяции) вычисляется значение функции одним из известных методов с требуемой точностью. Результаты расчетов представляются в виде таблицы, в одной из колонок которой приводятся значения аргумента, а в другой — соответствующее ему значение функции. Алгоритм расчета представляет собой цикл типа «До», так как число шагов обычно известно заранее, или сочетание циклов «До» и «Пока», если заданы требования к точности вычислений.
Пример 8.3.6. Составить таблицу значений функции y= x 2 +2x -4 для х, изменяющегося в диапазоне от 0 до 10 с шагом 0,5.
Решение. Введем обозначения: Xn – начальное значение аргумента, Xk – конечное значение аргумента, Dx – шаг приращения аргумента. Программа работает следующим образом (рис. 8.3.7):
Блок 1. Вводим исходные данные: Xn, Xk, Dx.
Блок 2. Присваиваем текущему значению аргумента х начальное значение Xn.
Блок 3. Вычисляем значение функции при текущем значении аргумента.
Блок 4. Выводим на экран или печать значения x и y.
Блок 5. Увеличиваем значение аргумента на величину шага.
Блок 6. Проверяем условие окончания цикла. Если условие выполняется, то есть текущее значение аргумента меньше конечного значения аргумента, то возвращаемся на блок 3 и повторяем вычислительную процедуру (блоки 3, 4, 5, 6).Если условие не выполняется, то конец программы.
алг Табулирование_функци
дано Xn, Xk, Dx
нц для х от Xn до Xk с шагом Dx
Пример 8.3.7. Вычислить сумму и произведение чисел натурального ряда от 2 до 100.
Решение. Введем обозначение Xn – начальное значение аргумента, N – число членов ряда, Dx – шаг, S – сумма чисел, P – произведение чисел.
Подпрограммы в Pascal
алг Вычисление суммы
нц для i от Xn до N с шагом Dx
В данном алгоритме (рис. 8.3.8) для вычисления суммы чисел переменной S до входа в цикл присваивается начальное значение нуль S=0, а для вычисления произведения переменной P присваивается начальное значение единица Р=1. В теле цикла проводится вычисление S: к текущему значению суммы прибавляется текущее значение переменной цикла S=S+i. Для вычисления произведения текущее значение произведения Р умножается на текущее значение переменной цикла – P=P*i.
Программа табулирования функции паскаль
Новый точечный рисунок.jpg
АиB промежуток, найти Y используя табуляцию
правильно ли я написл программу(решение есть) или еще что то добавить надо?
Const min=3; max=3; h=0.5; Var x,y:real; Function F(x:real):real; begin; F:=(exp(x)+exp(-x))/exp(x)-exp(-x); end; var i:integer;n:real; Begin; x:=min; for i:=min to max do begin; n:=(max-min)/h; y:=F(x); x:=x+h; end; writeln(‘x=’,x:5:5,», ‘y=’,y:5:5);writeln(‘n=’,n) end.
Последний раз редактировалось Stilet; 22.11.2013 в 21:53 .
Регистрация: 23.10.2010
Сообщений: 2,246
| правильно ли я написл программу |
Нет, не правильно.
min и max — это левая и правая границы области значений X. Тип — real.
Использовать эти значения для переменной цикла For нельзя, так как препод тутже изменит условие, например min = -3.1. И .
Шаг задан и вычислять n нет необходимости.
А для какой цели служит данный код в теле твоего цикла?
n:=(max-min)/h;
Пример решения:
xmin := -3; xmax := 3; h := 0.5; x := xmin; while x x := x + h; writeln(‘x =’, x:6:2, ‘ y = ‘, y:6:2); end; .
Регистрация: 02.03.2008
Сообщений: 2,537
И в описании функции скобки в знаменателе забыли. Внизу дроби..
Последний раз редактировалось type_Oleg; 22.11.2013 в 21:27 .
Пользователь
Регистрация: 25.12.2011
Сообщений: 96
Нет, не правильно.
min и max — это левая и правая границы области значений X. Тип — real.
Использовать эти значения для переменной цикла For нельзя, так как препод тутже изменит условие, например min = -3.1. И .
Шаг задан и вычислять n нет необходимости.
А для какой цели служит данный код в теле твоего цикла?
n:=(max-min)/h;
Пример решения:
xmin := -3; xmax := 3; h := 0.5; x := xmin; while x x := x + h; writeln(‘x =’, x:6:2, ‘ y = ‘, y:6:2); end; .
а в цикле for разве не так ,как я написал?
нахождение n хм. так сказать » препод намекнул» но в то же время n всегда 0
а в цикле for разве не так ,как я написал?
нахождение n хм. так сказать » препод намекнул» но в то же время n всегда 0
я делал с while но сказали for/
Нет, не правильно.
min и max — это левая и правая границы области значений X. Тип — real.
Использовать эти значения для переменной цикла For нельзя, так как препод тутже изменит условие, например min = -3.1. И .
Шаг задан и вычислять n нет необходимости.
А для какой цели служит данный код в теле твоего цикла?
n:=(max-min)/h;
Пример решения:
xmin := -3; xmax := 3; h := 0.5; x := xmin; while x x := x + h; writeln(‘x =’, x:6:2, ‘ y = ‘, y:6:2); end; .
делал вот по этому примеру только функция имела другую формулу
http://www.cyberforum.ru/pascalabc/thread999351.html
Последний раз редактировалось Stilet; 23.11.2013 в 13:24 .
Регистрация: 23.10.2010
Сообщений: 2,246
| я делал с while но сказали for/ |
Тогда понятно, зачем препод намекнул по поводу использования n.
В этом случае вычисляй n до входа в цикл, а затем в цикле for выполняй вычисления x и самой функции:
n := Round((Max — Min)/h); for i := 0 to n do begin x := Min + i * h; y := f(x); writeln( . ); end;
Использование функции Round() — нужно для совместимости типов данных. В выражении для n переменная h — real. Впринципе и Max с Min надо делать типа real.
Можно использовать и функции Int() или Trunc() (почитай про них).
Как-то так, .
PS: Подумай, может не стоит цитировать посты целиком. Они ведь и так видны.
Только те части сообщения имеет смысл цитировать, на которые даеш ответ.
Источник: www.programmersforum.ru
Программа табулирования функции в V ВА
Информатика для I курса (лабораторные работы) часть I: Учебное пособие по выполнению лабораторных работ по курсу ”Информатика” для студентов всех специальностей/ СПбГАСУ; Сост.: С. Н. Никифоров СПб., 2011. 94 с.
Учебное пособие предназначено для помощи студентам при выполнении лабораторных работ в среде Excel и VBA. Комментируются некоторые особенности программирования, приводятся и поясняются варианты программ.
Илл. 51. Библиогр.: 2 назв.
Рецензент д-р физ.-мат. наук, профессор Б.Г. Вагер
Информатика для I курса (лабораторные работы) часть I
Составитель: Никифоров Сергей Николаевич
СОДЕРЖАНИЕ
1. ТАБУЛИРОВАНИЕ ФУНКЦИИ.. 5
2. ТАБУЛИРОВАНИЕ РАЗВЕТВЛЯЮЩЕЙСЯ ФУНКЦИИ.. 9
3. ТАБУЛИРОВАНИЕ ФУНКЦИИ, РАЗВЕТВЛЯЮЩЕЙСЯ БОЛЬШЕ, ЧЕМ ОДИН РАЗ. 14
4. ТАБУЛИРОВАНИЕ ДВУХ ФУНКЦИЙ.. 20
5. ПОСТРОЕНИЕ ПОВЕРХНОСТИ.. 24
6. КВАДРАТИЧНЫЕ ФОРМЫ. 28
Часть первая. 28
6.1.1 Решение матричного уравнения в Excel. 28
6.1.2 Решение матричного уравнения в Excel с предварительным преобразованием. 32
6.1.3 Вычисление квадратичной формы в Excel. 32
6.1.4 Вычисление квадратичной формы с использованием матричных функций Excel. 35
6.1.5 Вычисление квадратичной формы с использованием матричных функций VBA. 36
Часть вторая. 37
6.2.1 Операции над массивами в Excel 37
6.2.2 Операции над массивами в VBA.. 39
7. ОПЕРАТОРЫ ЦИКЛА.. 41
8. ИГРА “УГАДАЙ ЧИСЛО”. 49
9. ПОЛЬЗОВАТЕЛЬСКИЕ ФОРМЫ. 52
9.1 Калькулятор с OptionButton. 52
9.2 Калькулятор с CheckBox. 56
9.3 Логарифмический калькулятор. 58
9.4 Решение квадратных уравнений. 61
9.5 Вычисление максимума, минимума, среднего арифметического, среднего геометрического и среднего гармонического. 64
9.6 Использование объекта ScrollBar (полоса прокрутки) 67
10. РАБОТА С ОБЪЕКТОМ LISTBOX.. 71
Часть первая. 71
10.1 Заполнение объектов ListBox, расположенных на одном объекте UserForm. 71
10.2 Заполнение объектов ListBox, расположенных на разных объектах UserForm. 76
10.2.1 Заполнение списка поэлементно, если список состоит из одной колонки. 76
10.2.2 Заполнение списка массивом, если список состоит из одной колонки. 78
10.2.3 Заполнение списка из диапазона, в который предварительно введены элементы списка 80
10.2.4 Заполнение списка поэлементно, если список состоит из нескольких колонок. 82
10.2.5 Заполнение списка массивом, если список состоит из нескольких колонок. 84
10.3 Заполнение объектов ListBox, расположенных на листе Excel 86
Программа Заполнение объектов ListBox, расположенных на листе Excel 87
Часть вторая. 88
10.4 Табулирование функций в объектах ListBox. 88
ВВЕДЕНИЕ
Настоящее издание предназначено для студентов первого курса, выполняющих лабораторные работы по курсу “Информатика”.
Осознавая масштабность курса, автор не претендует на всеобъемлемость материала, а, наоборот, даже не рассматривает некоторые разделы вообще, полагая, что при необходимости с ними можно ознакомиться в любом из фундаментальных учебников, изданных хотя бы в последнее время.
Основная задача – оказать помощь студентам при выполнении лабораторных работ в среде EXCEL и VBA.
Вместе с тем автор считает целесообразным отметить обязательность посещения лекций по курсу “Информатика”, в соответствии с которым и формируются тексты программ, усложняющиеся по мере освоения средств и возможностей VBA.
ТАБУЛИРОВАНИЕ ФУНКЦИИ
Выполнение лабораторной работы “Табулирование функции” состоит из двух частей:
– табулирование функции в Excel;
– табулирование функции в VBA.
Критерием правильности является совпадение полученных таблиц.
Процесс табулирования функции в Excel описан во многих монографиях, одной из которых является книга А. Гарнаева “ ”. Но на некоторые моменты хотелось бы обратить внимание.
Значение первой ячейки таблицы в принципе может быть любым, но, как правило, оно выбирается в соответствии с вариантом задания.
Главное – оно задается КОНСТАНТОЙ!
В рассматриваемом примере, рис. 1.1, такой ячейкой является А6, а значение константы – (минус) 2.
Адрес и значение ячейки, в которой хранится величина шага изменения аргумента табулируемой функции также, в принципе, произвольны, но значение обязательно – КОНСТАНТА.
В рассматриваемом примере такой ячейкой является B 4, а значение константы 0,25. (Если константа задается дробью, то она должна “прижаться” к правой стенке ячейки иначе она воспринимается как символьная константа, а не как цифровая. Достигается это заменой неправильно выбранного знака-разделителя дробной части от целой – точки на запятую).
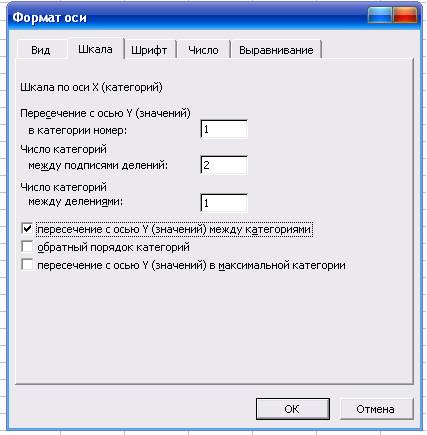
Обязательным является получение графика в виде, представленном на рис. 1.1, когда кривая графика начинается от оси Y, а маркеры кривой графика (если щелкнуть по кривой) совпадают с рисками и подписями оси X, сравните с графиком рис. 1.2.


Чтобы от графика рис. 1.2 перейти к графику рис. 1.1 необходимо в Excel: дважды щелкнуть по оси X, в появившемся окне “Формат оси” рис. 1.3 убрать флажок в разделе “пересечение с осью Y (значений) между категориями” и нажать OK.
Программа табулирования функции в V ВА
Дата добавления: 2019-03-09 ; просмотров: 647 ; Мы поможем в написании вашей работы!
Поделиться с друзьями:
Источник: studopedia.net