Программа схема эль гамаля

Данный текст будет являться одной из переписанных глав для учебного пособия по защите информации кафедры радиотехники и систем управления, а также, с этого учебного кода, кафедры защиты информации МФТИ (ГУ). Полностью учебник доступен на github (см. также draft releases). На Хабре планирую выкладывать новые «большие» куски, во-первых, чтобы собрать полезные комментарии и замечания, во-вторых, дать сообществу больше обзорного материала по полезным и интересным темам. Предыдущие разделы главы «Криптографически протоколы»: 1, 2, 3

Как и создатели трёхпроходных протоколов из предыдущего раздела, авторы следующих алгоритмов считали их не просто математическими конструкциями, обеспечивающие некоторую элементарную операцию (например, шифрование с открытым ключом), но пытались вокруг одной-двух формул построить законченную систему распространения ключей. Некоторые из этих конструкций, преобразовавшись, используются до настоящего времени (например, протокол Диффи-Хеллмана), некоторые — остались только в истории криптографии и защиты информации.

Шифр Эль Гамаля

Позже в 1990-х годах будут разделены математические асимметричные примитивы (шифрование и электронная подпись) и протоколы, эти примитивы использующие, что будет продемонстрировано в разделе про асимметричные протоколы.

Протокол Диффи—Хеллмана

Первый алгоритм с открытым ключом был предложен Диффи и Хеллманом в работе 1976 года «Новые направления в криптографии» (Bailey Whitfield Diffie, Martin Edward Hellman, «New directions in cryptography», [Diffie, Hellman 1976]). Данный протокол, который также можно назвать схемой Диффи—Хеллмана, стал первым, позволивший уменьшить требования к каналу связи для установления защищённого соединения без предварительного обмена ключами.

Протокол позволяет двум сторонам создать общий сеансовый ключ используя такой канал связи, который может прослушивать злоумышленник, но в предположении, что последний не может менять содержимое сообщений.

Пусть — большое простое число, — примитивный элемент группы , , причём , и известны заранее. Функцию считаем однонаправленной, то есть вычисление функции при известном значении аргумента является лёгкой задачей, а её обращение (нахождение аргумента) при известном значении функции — трудной. (Обратную функцию называют функцией дискретного логарифма. В настоящий момент не существует быстрых способов вычисления такой функции для больших простых .)

Протокол обмена состоит из следующих действий.

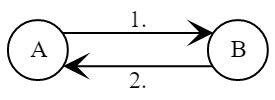
1. Алиса выбирает случайное
2. Боб выбирает случайное
   Боб вычисляет сессионный ключ
3. Алиса вычисляет

Протокол обеспечивает только генерацию новых сессионных ключей (цель G10). В отсутствие третей доверенной стороны он не обеспечивает ни аутентификацию сторон (цель G1), из-за отсутствия проходов с подтверждением владения ключом отсутствует аутентификация ключа (цель G8). Зато, так как протокол не использует длительные «мастер»-ключи, можно говорить о том, что он обладает свойством совершенной прямой секретности (цель G9).

Шифрование по алгоритму Эль-Гамаля

Протокол можно использовать только с такими каналами связи, в которые не может вмешаться активный криптоаналитик. В противном случае протокол становится уязвим к простой «атаке посередине».

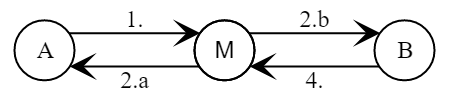
1. Алиса выбирает случайное
2. Меллори выбирает случайное
   Меллори вычисляет сессионный ключ для канала с Алисой

Протокол Диффи—Хеллмана отличается от большей части протоколов распространения ключей из-за того, что не использует другие криптографические примитивы (функции шифрования, электронно-цифровой подписи или хеширования), но сам по себе является в некотором смысле криптографическим примитивом для построения более сложных протоколов. Он обеспечивает генерацию случайного числа в распределённой системе без доверенного центра. Причём ни одна из сторон не может заставить другую сторону использовать старый сессионный ключ, в отличие от, например, протокола Yahalom.

Протокол можно изменить таким образом, чтобы вместо мультипликативной группы простого умножения использовать аддитивную группу сложения точек эллиптической кривой. В этом случае стороны по прежнему будут выбирать некоторые случайные целые числа, но не возводить генератор-число в степень, а умножать генератор-точку на загаданное число.

1. Стороны договорились о группе точек эллиптической кривой , её циклической подгруппе мощности и генераторе группы (или хотя бы достаточно большой подгруппы группы ).
2. Алиса выбирает случайное
3. Боб выбирает случайное
   Боб вычисляет точку
4. Алиса вычисляет точку

Протокол Эль-Гамаля

Протокол Эль-Гамаля ([ElGamal, 1984], [ElGamal, 1985]) за счёт предварительного распространения открытого ключа одной из сторон обеспечивает аутентификацию ключа для этой стороны. Можно гарантировать, что только владелец соответствующего закрытого ключа сможет вычислить сеансовый ключ. Однако подтверждение факта получение ключа (выполнение целей G1 и G8) не является частью протокола.

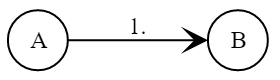
Алиса и Боб выбирают общие параметры и , где — большое простое число, а — примитивный элемент поля .
Боб создаёт пару из закрытого и открытого ключей и :

Протокол MTI/A(0)

В 1986 году Ц. Мацумото (Tsutomu Matsumoto), И. Такашима (Youichi Takashima) и Х. Имаи (Hideki Imai) предложили несколько алгоритмов, позже названных семейством протоколов MTI ([Matsumoto, Tsutomu, Imai 1986]). За счёт предварительного распространения открытых ключей обоих сторон они обеспечивали неявную аутентификацию ключа (цель G7). То есть сессионный ключ гарантированно мог получить только владельцы соответствующих открытых ключей. Мы рассмотрим одного из представителей данного семейства — протокол MTI/A(0).

Предварительно стороны договорились об общих параметрах системы и , где — большое простое число, а — примитивный элемент поля .

Каждая из сторон (Алиса и Боб) сгенерировала пару из закрытого и открытого ключей:

1. Алиса сгенерировала случайное число
2. Боб сгенерировал случайное число
   Боб вычислил сеансовый ключ
3. Алиса вычислила сеансовый ключ

Из-за сложности задачи дискретного логарифмирования злоумышленник не сможет получить или из передаваемых сообщений, а предварительная публикация открытых ключей гарантирует, что сессионный ключ получат только легальные пользователи. Случайный выбор и гарантирует, что обе стороны могут быть уверены в создании нового сессионного ключа в каждом сеансе протокола.

Как и другие представители криптосистем-протоколов, MTI не разрабатывался с учётом возможности компрометации закрытых «мастер»-ключей и (цель G9).

Протокол Station-to-Station

Протокол STS (Station-to-Station, [Diffie, Oorschot, Wiener 1992]) предназначен для систем мобильной связи. Он использует идеи протокола Диффи—Хеллмана и криптосистемы RSA. Особенностью протокола является использование механизма электронной подписи для взаимной аутентификации сторон.

Предварительно стороны договорились об общих параметрах системы и , где — большое простое число, а — примитивный элемент поля .

Каждая из сторон и обладает долговременной парой ключей: закрытым ключом для расшифрования и создания электронной подписи и открытым ключом для шифрования и проверки подписи .

Где это функция проверки электронной подписи на открытом ключе , а — функция расшифрования с использованием закрытого ключа .

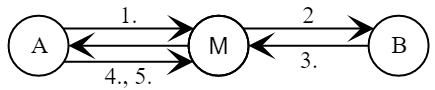
Протокол состоит из четырёх проходов, три из которых включают передачу сообщений ([Черёмушкин 2009]).

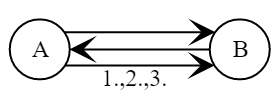
1. Алиса выбирает случайное число .
2. Боб выбирает случайное число .
   Боб вычисляет сессионный ключ .
3. Алиса вычисляет сессионный ключ .
   Алиса проверяет подпись в сообщении .
4. Боб проверяет подпись в сообщении .

Как показала атака Лоу 1996 года ([Lowe 1996]), протокол не может гарантировать аутентификацию субъектов (цель G1), ключей (G7) и подтверждение владения сессионным ключом (G8). Хотя злоумышленник не может получить доступ к новому сессионному ключу, если протокол использовать только для аутентификации субъектов, Алиса может принять злоумышленника за Боба.

Алиса выбирает случайное число .

Как и все остальные «криптосистемы-протоколы», протокол Station-to-Station основывается на некотором внешнем источнике информации об открытых ключах участников, не подвергая сомнению корректность и надёжность этого источника. Что, в общем случае, неверно. Если информация о ключах участников нужно получать извне при каждом сеансе протокола (например, если участников много, и запомнить ключи всех возможности нет), то канал получения открытых ключей будет основной целью активного криптоаналитика для рассмотренных протоколов. Как от этого защититься с использованием примитивов асимметричной криптографии — в следующем разделе.

Литература

Источник: habr.com

Реализация шифрования дешифрования методом Эль-Гаммеля

1.Текст задания, с указанием номера студента в журнале и соответствующих вариантов задания.

2.Краткое описание алгоритма шифра Эль-Гамаля.

3.Реализация шифрования/дешифрования методом Эль-Гамаля.

3.1.Описание основных функций и переменных.

3.2.Результаты выполнения программы.

4. Краткое описание алгоритма электронной подписи Диффи-Хеллмана.

5. Реализация алгоритма подписи сообщения c помощью системы Диффи-Хеллмана.

5.1. Описание основных функций и переменных.

5.2. Результаты выполнения программы.

6. Краткое описание алгоритма RC4.

7. Реализация алгоритма RC4.

7.1. Описание основных функций и переменных.

7.2. Результаты выполнения программы.

1.Текст задания, с указанием номера студента в журнале и соответствующих вариантов задания

. Программно реализовать на языке C++ алгоритм шифрования и дешифрования сообщения c помощью метода в соответствии с вариантом. Номер варианта k определяется по формуле: k=N mod 4, где N=11 – номер студента в журнале.

K=1

Метод шифрования «Шифр Эль-Гамаля»Программно реализовать на языке C++ алгоритм электронной подписи сообщения и проверки его подлинности c помощью метода в соответствии с вариантом. Номер варианта k определяется по формуле: k=N mod 3, где N – номер студента в журнале.

K=2

Система Диффи-Хелмана

Программно реализовать на языке C++ алгоритм шифрования и дешифрования сообщения c помощью потокового шифра RC4.

Краткое описание алгоритма шифра Эль-Гамаля.

Схема Эль-Гамаля (Elgamal) — криптосистема с открытым ключом, основанная на трудности вычисления дискретных логарифмов в конечном поле. Криптосистема включает в себя алгоритм шифрования и алгоритм цифровой подписи.

Схема была предложена Тахером Эль-Гамалем в 1984 году. Эль-Гамаль разработал один из вариантов алгоритма Диффи-Хеллмана. Он усовершенствовал систему Диффи-Хеллмана и получил два алгоритма, которые использовались для шифрования и для обеспечения аутентификации. В отличие от RSA алгоритм Эль-Гамаля не был запатентован и, поэтому, стал более дешевой альтернативой, так как не требовалась оплата взносов за лицензию. Считается, что алгоритм попадает под действие патента Диффи-Хеллмана.

Генерация ключей

1. Генерируется случайное простое число длины битов.

2. Выбирается случайное целое число такое, что .

3. Выбирается случайное целое число такое, что .

5. Открытым ключом является тройка , закрытым ключом — число .

Работа в режиме шифрования

Шифрсистема Эль-Гамаля является фактически одним из способов выработки открытых ключей Диффи — Хеллмана. Шифрование по схеме Эль-Гамаля не следует путать с алгоритмом цифровой подписи по схеме Эль-Гамаля.

Шифрование

Сообщение шифруется следующим образом:

1. Выбирается сессионный ключ — случайное целое число такое, что

2. Вычисляются числа и .

3. Пара чисел является шифротекстом.

Нетрудно видеть, что длина шифротекста в схеме Эль-Гамаля длиннее исходного сообщения вдвое.

Расшифрование

Зная закрытый ключ , исходное сообщение можно вычислить из шифротекста по формуле:

При этом нетрудно проверить, что

Для практических вычислений больше подходит следующая формула:

Пример

1. Допустим что нужно зашифровать сообщение .

2. Произведем генерацию ключей :

1. пусть . Выберем — случайное целое число такое,что .

3. Итак , открытым является тройка ,а закрытым ключом является число .

3. Выбираем случайное целое число такое, что 1 < k < (p − 1). Пусть .

4. Вычисляем число .

5. Вычисляем число .

6. Полученная пара является шифротекстом.

1. Необходимо получить сообщение по известному шифротексту и закрытому ключу .

2. Вычисляем M по формуле :

3. Получили исходное сообщение .

Так как в схему Эль-Гамаля вводится случайная величина ,то шифр Эль-Гамаля можно назвать шифром многозначной замены. Из-за случайности выбора числа такую схему еще называют схемой вероятностного шифрования. Вероятностный характер шифрования является преимуществом для схемы Эль-Гамаля, так как у схем вероятностного шифрования наблюдается большая стойкость по сравнению со схемами с определенным процессом шифрования. Недостатком схемы шифрования Эль-Гамаля является удвоение длины зашифрованного текста по сравнению с начальным текстом. Для схемы вероятностного шифрования само сообщение и ключ не определяют шифротекст однозначно. В схеме Эль-Гамаля необходимо использовать различные значения случайной величины для шифровки различных сообщений и . Если использовать одинаковые , то для соответствующих шифротекстов и выполняется соотношение . Из этого выражения можно легко вычислить , если известно .

Реализация шифрования дешифрования методом Эль-Гаммеля

Источник: stydopedia.ru

отчет эль гамаль1. Система шифрования данных ЭльГамаля

Единственный в мире Музей Смайликов

Самая яркая достопримечательность Крыма

Скачать 1.54 Mb.

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

ФАКУЛЬТЕТ ПРИКЛАДНОЙ МАТЕМАТИКИ, ИНФОРМАТИКИ И МЕХАНИКИ

КАФЕДРА ERP-СИСТЕМ И БИЗНЕС ПРОЦЕССОВ

по лабораторной работе № 1

«Система шифрования данных Эль-Гамаля»

студент 2-го курса 11-ой группы

Аникеев Н. Г.
Проверил:

доц. Воронков Б. Н.

Постановка задачи

• Ознакомиться с обучающей программой «ElgamalTutor».
• Изучить и описать алгоритм Эль-Гамаля.
• Зафиксировать последовательность этапов и результаты обучения.
• Провести исследование программы с целью выявления ошибок и недочетов.
• Сформулировать принципы работы алгоритма Эль-Гамаля.
• Ответить на контрольные вопросы.
• Составить отчет о проделанной работе.

1. Описание алгоритма Эль-Гамаль
Схема Эль-Гамаля (Elgamal) — криптосистема с открытым ключом, основанная на трудности вычисления дискретных логарифмов в конечном поле. Криптосистема включает в себя алгоритм шифрования и алгоритм цифровой подписи. Схема Эль-Гамаля лежит в основе бывших стандартов электронной цифровой подписи в США (Digital Signature Algorithm) и России (ГОСТ Р 34.10-94).

Схема была предложена Тахером Эль-Гамалем в 1985 году.

В настоящее время криптосистемы с открытым ключом считаются наиболее перспективными. К ним относится и схема Эль-Гамаля, криптостойкость которой основана на вычислительной сложности проблемы дискретного логарифмирования, где по известным p, g и y требуется вычислить x, удовлетворяющий сравнению:

ГОСТ Р34.10-1994, принятый в 1994 году в Российской Федерации, регламентировавший процедуры формирования и проверки электронной цифровой подписи, был основан на схеме Эль-Гамаля. С 2001 года использовался новый ГОСТ Р 34.10-2001, использующий арифметику эллиптических кривых, определенных над простыми полями Галуа. Существует большое количество алгоритмов, основанных на схеме Эль-Гамаля: это алгоритмы DSA (Digital Signature Algorithm), ECDSA (Elliptic Curve Digital Signature Algorithm), KCDSA (Korean Certificate-based Digital Signature Algorithm), схема Шнорра[1].

В 2015 г. вместе с новым алгоритмом «Кузнечик» один из вариантов алгоритма ГОСТ-89 был опубликован под названием «Магма» как часть стандарта ГОСТ Р 34.12-2015.

2. Результат обучения
Начальные данные: вариант № ?

Открытый текст – Академик
1. Запустили режим обучения

2. Обучение возведению в степень по модулю

4. Нахождение обратного по модулю

5. Краткая историческая справка

6. Описание схемы Эль-Гамаля

7. Изучаем как генерируются ключи в алгоритме

8. Шифруем сообщение

9. Расшифровываем сообщение

11. Тест по теории

12. Итог, выданный программой

3. Выявление ошибок в обучающей программе
В результате тестирования были выявлены следующие недочеты:

1*. Во многих окнах, в том числе в окне «тест простоты» не фильтруются вводимые символы

2*. Тест на простоту числа «падает» при вводе простого числа со знаком отрицания

3. Неудобное переключение между окнами — каждое новое окно запускается в левом верхнем углу.

4. Не кросплатформенное приложение.

5. Устаревшее описание. Не актуальные алгоритмы.

*ошибки из старой версии программы, в новой исправлены
4. Принципы работы алгоритма Эль-Гамаля

Схема работы алгоритма Эль-Гамаля изображена на рисунке, приведённом ниже[2].

Ответы на контрольные вопросы

43: Что такое информационная безопасность?
Информационная безопасность – состояние информации, информационных ресурсов и информационных систем, при которой с требуемой вероятностью обеспечивается защита информации[4].
45: Перечислите возможные виды утечек информации.
а) разглашение;

б) несанкционированный доступ к информации;

в) разведка.
58: Что такое криптосистема Эль Гамаля?
Криптосистема Эль Гамаля — алгоритм шифрования, базирующийся на сложности решения задачи дискретного логарифмирования. [4]
60: В чем заключается режим вероятностного шифрования в алгоритме Эль Гамаля?
Вероятностное шифрование — это принцип шифрования, главной особенностью которого является то, что один и тот же исходный открытый текст, преобразованный на одном и том же ключе, приводит к появлению множества различных шифрованных текстов [3].
C ≡ α^r (mod p ) ; 2 C ≡ (M * β^r )(mod p) ; r – рандо-

мизатор – случайное целое число из интервала 1≤ r ≤ ( p 2), необходи-

мое для реализации схемы вероятностного шифрования [4]
65: Докажите корректность алгоритма Эль Гамаля.

Выводы
В результате ознакомления с обучающей программой «ElgamalTutor», изучен алгоритм шифрования Эль Гамаля, пройден тест на понимание основных математических операций, использующихся в алгоритме, сформулированы принципы работы алгоритма. Также проведено исследование обеих версий программы (тестирование) и выявлены ошибки и недочеты (в том числе и критичные). Приведенные ответы на контрольные вопросы позволили расширить представление об особенностях асимметричного шифрования.

Список использованных источников

• Ковун В. Обучающая компьютерная программа для изучения алгоритма шифрования Эль-Гамаля / В. Ковун – [электронный ресурс] PUBLIC (\HYPERLINK «file://fs/PUBLIC»fsHYPERLINK «file://fs/PUBLIC»HYPERLINK «file://fs/PUBLIC»PUBLIC) \fsPUBLIC2HYPERLINK «file://fs/PUBLIC/2к-МАГ-2017/Ковун/ElgamalTutor.exe»к-МАГ-2017КовунElgamalTutor.exe
• Схема Эль-Гамаля – (URL: https://ru.wikipedia.org/wiki/Схема_Эль-Гамаля) (дата обращения 27.09.2017).
• Вероятностное шифрование — (URL: http://cryptowiki.net/index.php?title=HYPERLINK «http://cryptowiki.net/index.php?title=Вероятностное_шифрование»Вероятностное_шифрование)(дата обращения 04.10.2017)
• Воронков Б. Н. Криптографические методы защиты информации: учебное пособие для вузов / Б. Н. Воронков. — Воронеж: ВГУ, 2008. — 60.
• Остаток числа в степени по модулю — (URL — http://www.abakbot.ru/online-16/254-ostatok-chisla-v-stepeni) (дата обращения 11.10.2017)
• Онлайн калькулятор: обратный элемент в кольце по модулю — (URL — https://planetcalc.ru/3311/) (дата обращения 11.10.2017)

Источник: topuch.com