ВУЗ: МЭИ (Московский энергетический институт)
Факультет: ЭнМИ (Институт энергомашиностроения и механики)
Предмет: Теоретическая механика
Тип документа: Программы
Формат файла: .rar
Размер: 9.148 Мб
Добавлен: 20.03.2018 20:29:50
Отправляю Вам программы для решения задач статики и кинематики на компьютере.
1, 2, или 3 папка
Необходимо установить либо Максиму или вольфрам математику или программу STEVIN
Результаты решения должны быть распечатаны.
Робота должна быть оформлена с титульным листом на котором должно быть указано номер гр вариант задания итд
(распеч на принтере ) вручную без титульника работа не принимается
Дополнительно сайты для изучения теоретической механики
С уважением Комерзан Евгений Владиславович, доцент каф. Робототехники, мехатроники, динамики и прочности машин.
В архиве программы для решения задач по теоретической механике:
Источник: 5tb.info
Как решить любую задачу по механике. Алгоритм
Приложения для просмотра файлов учебных заданий
Приложения для просмотра файлов учебных заданий по разделам механики в форматах PDF и DjVu, которые можно скачать с официальных сайтов.
Если скачанные с нашего сайта файлы не открываются, то возможно на Вашем компьютере не установлено одно из следующих приложений:
Adobe Reader

Adobe Reader представляет собой международный стандарт для просмотра файлов PDF. Это программа просмотра файлов PDF, позволяющая открывать любые документы PDF и работать с ними. С помощью Adobe Reader можно просматривать, проверять и печатать файлы PDF, а также выполнять в них поиск, добавлять к ним цифровую подпись и открывать их для совместной работы.
WinDjView

WinDjView — это быстрая и компактная программа для просмотра файлов формата DjVu под Windows с вкладками для документов, непрерывной прокруткой страниц и расширенными возможности печати. WinDjView основана на свободно распространяемой библиотеке DjVuLibre. Формат DjVu позволяет сохранять документы и картинки с высоким качеством в файлы малого размера.
Источник: isopromat.ru
Задачи по теоретической механике с подробными решениями
Здесь собраны основные примеры задач с решениями по теоретической механике. Рядом с условием задачи приводится ссылка на страницу с ее подробным решением и ответом. Задачи охватывают следующие разделы технической и теоретической механики: статика, кинематика, динамика материальной точки и системы тел.
Подробные решения задач по теоретической механике
Здесь приводятся условия задач по теоретической механике, имеющие подробные решения с ответами. Задачи сгруппированы по основным разделам теоретической механики: статика, кинематика и динамика. Чтобы посмотреть решение, нажмите на соответствующую ссылку в конце условия.
Определение реакций опор простой рамы
Статика
Условия задач
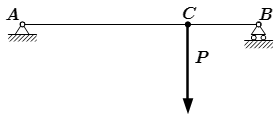
Найти графическим способом реакции опор балки AB , на которую действует сила P , приложенная в точке C .
Дано: P = 55 kH , AB = 10 м , AC = 7 м , BC = 3 м .
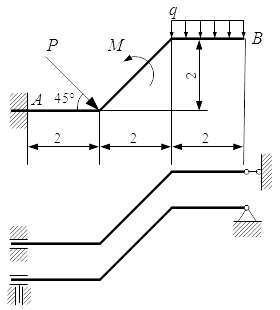
Найти реакции опор для того способа закрепления, при котором момент MA в опоре A имеет наименьшее значение.
Решение
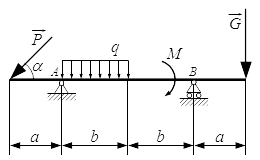
Найти реакции опор балки.
Решение
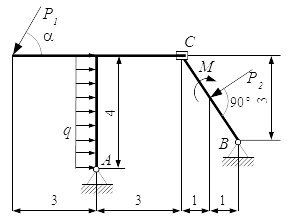
Найти реакции опор составной конструкции.
Решение
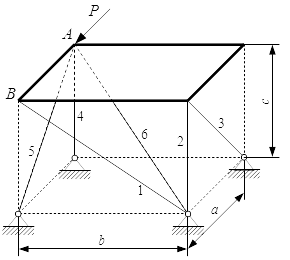
Определить реакции стержней, поддерживающих тонкую однородную прямоугольную плиту в трехмерном пространстве.
Решение
Кинематика
Кинематика материальной точки
Определение скорости и ускорения точки по заданным уравнениям ее движения
Дано: Уравнения движения точки: x = 12 sin( πt/ 6) , см; y = 6 cos 2 ( πt/ 6) , см.
Установить вид ее траектории и для момента времени t = 1 с найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Поступательное и вращательное движение твердого тела
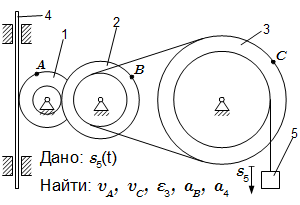
Дано:
t = 2 с; r1 = 2 см, R1 = 4 см; r2 = 6 см, R2 = 8 см; r3 = 12 см, R3 = 16 см; s5 = t 3 – 6t (см).
Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.
Кинематический анализ плоского механизма
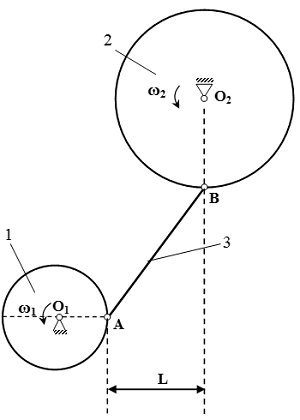
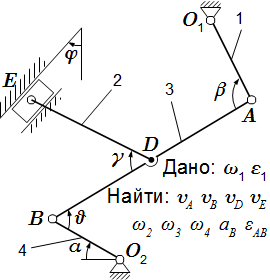
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна E. Стержни соединены с помощью цилиндрических шарниров. Точка D расположена в середине стержня AB.
Дано: ω1, ε1.
Найти: скорости VA, VB, VD и VE; угловые скорости ω2, ω3 и ω4; ускорение aB; угловое ускорение εAB звена AB; положения мгновенных центров скоростей P2 и P3 звеньев 2 и 3 механизма.
Определение абсолютной скорости и абсолютного ускорения точки
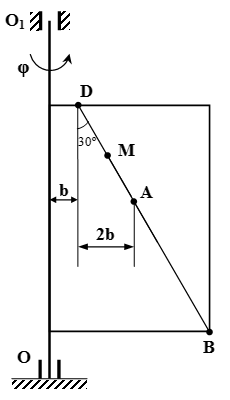
Прямоугольная пластина вращается вокруг неподвижной оси по закону φ = 6 t 2 – 3 t 3 . Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. Ось вращения OO 1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD движется точка M . Задан закон ее относительного движения, т. е. зависимость s = AM = 40( t – 2 t 3 ) – 40 ( s — в сантиметрах, t — в секундах). Расстояние b = 20 см . На рисунке точка M показана в положении, при котором s = AM > 0 (при s < 0 точка M находится по другую сторону от точки A ).
Найти абсолютную скорость и абсолютное ускорение точки M в момент времени t 1 = 1 с .
Динамика
Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
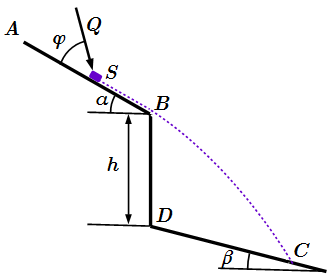
Груз S, рассматриваемый как материальная точка массы m = 5кг, движется по шероховатой поверхности от точки A до точки B, в которой отрывается от поверхности и продолжает движение в воздухе до падения на наклонную поверхность в точке C. Движение происходит в плоскости рисунка.
В точке A, груз имел скорость vA = 1 м/с. Скорость в точке B: vB = 4 м/с. Участок AB представляет собой плоскую поверхность с углом наклона α = 30° к горизонту. На участке AB, кроме силы тяжести и силы трения, на груз действует постоянная сила Q = 10 Н, направленная под углом φ = 45° к поверхности. Коэффициент трения f = 0,1 .
На участке BC, груз движется под действием только силы тяжести. Сопротивлением воздуха пренебречь. Поверхность, на которую падает груз, является плоской с углом наклона β = 15° к горизонту (см. рисунок). Точка D расположена ниже точки B на расстояние |BD| = h = 1 м .
Найти: Время движения tAB на участке AB; длину этого участка; время падения tBC от точки B к точке C; расстояние |DC|; уравнение траектории BC.
Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил
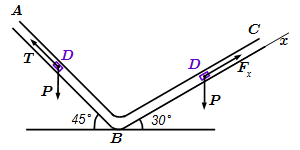
Груз D массой m, получив в точке A начальную скорость V0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости. На участке AB, длина которого l, на груз действует постоянная сила T(ее направление показано на рисунке) и сила R сопротивления среды (модуль этой силы R = μV 2 , вектор R направлен противоположно скорости V груза).
Груз, закончив движение на участке AB, в точке B трубы, не изменяя значения модуля своей скорости, переходит на участок BC. На участке BC на груз действует переменная сила F, проекция Fx которой на ось x задана.
Считая груз материальной точкой, найти закон его движения на участке BC, т.е. x = f(t), где x = BD. Трением груза о трубу пренебречь.
Теорема о движении центра масс системы
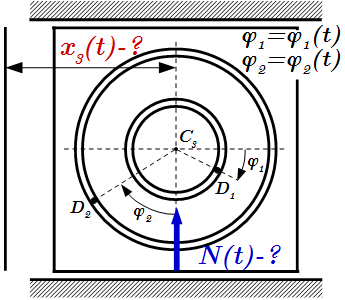
Механическая система состоит из грузов D1, D2 и прямоугольной вертикальной плиты, движущейся вдоль горизонтальных направляющих. В момент времени t0=0, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющим собой окружности.
Считая грузы материальными точками, и пренебрегая всеми сопротивлениями, определить закон движения плиты x3=f3(t) и полной нормальной реакции направляющих N=f(t) .
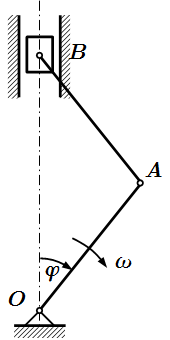
В кривошипно-шатунном механизме кривошип OA и шатун AB представляют собой однородные стержни массой m 1 и длиной l . Ползун B массой m 2 движется в вертикальных направляющих. Определить вертикальную составляющую реакции шарнира O в функции угла φ , если кривошип вращается с постоянной угловой скоростью ω . Трением в направляющих ползуна пренебречь.
Теорема об изменении количества движения системы
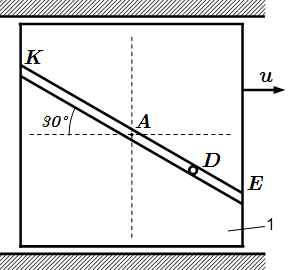
Механическая система состоит из прямоугольной вертикальной плиты 1, движущейся вдоль горизонтальных направляющих, и груза D. В момент времени t0=0, когда скорость плиты u0, груз под действием внутренних сил начинает двигаться по прямолинейному желобу плиты. При этом расстояние s=AD изменяется по закону s= 0,6 cos( πt 2 /4) .
Считая груз материальной точкой, и пренебрегая всеми сопротивлениями, определить скорость плиты u1 в момент времени t1.
Теорема об изменении кинетического момента системы
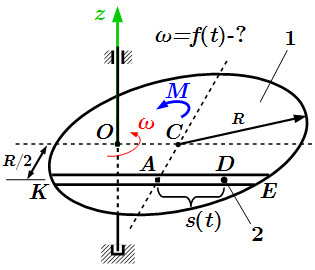
Однородная круглая радиуса R = 1,2 м горизонтальная платформа массой m1 = 24 кг вращается с угловой скоростью ω0 = 10 с -1 вокруг вертикальной оси z, отстоящей от центра масс C платформы на расстоянии OC = b = R/2 .
В момент времени t0 = 0 с по желобу платформы, под действием внутренних сил, начинает двигаться груз D массой m2 = 10 кг по закону s = AD = 0,6t 3 , где s выражено в метрах, t – в секундах. Одновременно на платформу действует пара сил с моментом M = 2 + 3t 2 (в ньютон-метрах).
Определить зависимость угловой скорости платформы как функцию времени.
Решение
Через блок перекинут канат; за точку A каната ухватился человек, к точке B подвязан груз одинаковой массы с человеком. Что произойдет с грузом, если человек станет подниматься по канату со скоростью v относительно каната? Масса блока в четыре раза меньше массы человека, и равномерно распределена по его ободу. Решение
Теорема об изменении кинетической энергии механической системы
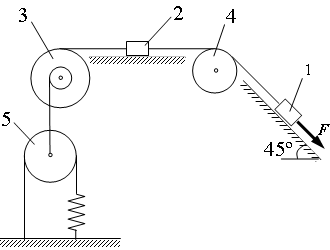
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3, блока 4 и подвижного блока 5. Заданы радиусы ступеней и радиусы инерции шкива 3 и блока 4. Блок 5 считать сплошным однородным цилиндром. Коэффициент трения груза 2 о плоскость f = 0,1 . Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3. Участки нитей параллельны соответствующим плоскостям. К подвижному блоку 5 прикреплена пружина с коэффициентом жесткости с .
Под действием силы F = f ( s ) , зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя. Деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент M сил сопротивления (от трения в подшипниках).
Заданы массы тел m 1 , m 2 , m 3 , m 4 , m 5 , коэффициент жесткости пружины c , зависимость силы от перемещения F = f ( s ) , величина момента M .
Определить значение центра масс тела 5 VC 5 в тот момент времени, когда перемещение s груза 1 станет равным s 1 = 0,2 м .
Применение общего уравнения динамики к исследованию движения механической системы
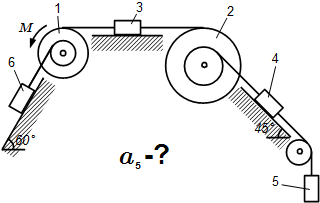
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м , приложенной к шкиву 1. Заданы радиусы ступеней шкивов, их радиусы инерции относительно осей вращения, а также веса шкивов и грузов. Грузы, веса которых равны нулю, на чертеже не изображать.
Пренебрегая трением, определить ускорение груза 5 .
Применение принципа Даламбера к определению реакций опор вращающегося тела
Вертикальный вал AK, вращающийся равномерно с угловой скоростью ω = 10 с -1 , закреплен подпятником в точке A и цилиндрическим подшипником в точке K.
К валу жестко прикреплены невесомый стержень 1 длиной l1 = 0,3 м, на свободном конце которого расположен груз массой m1 = 4 кг, и однородный стержень 2 длиной l2 = 0,6 м, имеющий массу m2 = 8 кг. Оба стержня лежат в одной вертикальной плоскости. Точки прикрепления стержней к валу, а также углы α и β заданы. Размеры AB=BD=DE=EK=b, где b = 0,4 м. Груз принять за материальную точку.
Пренебрегая массой вала, определить реакции подпятника и подшипника.
Источник: 1cov-edu.ru