Программа решение уравнения методом деления отрезка пополам

У меня студенты очень часто заказывают лабораторные работы, связанные с программированием высшей математики. Поэтому решил написать эту статью-шпаргалку, в которой поясню, как использовать метод деления отрезка пополам при приближенном нахождении корня уравнения.

➡ Сразу отмечу, что метод бисекции находит приближенное значение корня некоторого нелинейного уравнения.

Уравнение вида $k cdot x + b = 0$, где $k, b$ — действительные числа, называется линейным. Следовательно, любые уравнения другого вида можно считать нелинейными.

➡ Также нужно помнить, что метод за один запуск может найти с заданной точностью какой-то один корень. Если уравнение имеет несколько корней, например, $3$ штуки, то для нахождения их всех метод бисекции нужно запускать минимум $3$ раза.

Рассмотрю алгоритм в общем виде. Например, задано некое нелинейное уравнение $f(x) = 0$. Моя цель — найти хотя бы один корень этого уравнения, используя метод деления отрезка пополам.

Численное решение уравнений, урок 2/5. Метод деления отрезка пополам

Рассмотрю функцию $y = f(x)$ и построю ее график в прямоугольной системе координат.

График мне нужен, чтобы отделить корень на некотором, достаточно малом отрезке $[a; b]$.

Рисунок — график заданной функции $y = f(x)$ в общем виде

Из графика видно, что он пересекает ось абсцисс $2$ раза, следовательно, исследуемое нелинейное уравнение $f(x) = 0$ имеет $2$ различных корня.

Рисунок — график функции пересекает ось $Ox$ в двух точках

Я планирую поработать с корнем #2.

➡ То есть перед тем, как непосредственно запускать метод бисекции, приходится проводить подобную графоаналитическую работу.

Мне надо взять такой отрезок на оси абсцисс, который содержит корень #2. Если этого не сделать ( или сделать неправильно ), то метод деления отрезка пополам не сработает так, как надо.

Допустим выбрали такой отрезок $[a; b]$:

Рисунок — этап отделения корня. Отрезок $[a; b]$ содержит корень #2

➡ Вся работа метода деления отрезка пополам будет происходит в рамках этого отрезка $[a; b]$. Поэтому очень важно, чтобы заданная функция $y = f(x)$ была непрерывна на этом отрезке.

Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.

Итак, для отделения корня нужно выбрать такой отрезок, на котором анализируемая функция существует в любой точке этого отрезка. В данной статье я выбрал графоаналитический способ, но существуют и другие, например, через взятие производной. Не существует однозначного правила, как наиболее эффективно выбрать нужный отрезок для метода бисекции. Эта проблема ложится на плечи решающего. Поэтому будьте готовы к тому, что вам придется постоянно решать эту проблему, когда применяете метод деления отрезка пополам.

Итак, на выбранном отрезке $[a; b]$, рассматриваемая функция $y = f(x)$ непрерывна. Посмотрим на знак значений функции на концах отрезка, то есть посмотрим знак значений $f(a)$ и $f(b)$.

Рисунок — смотрим на значение функции на концах отрезка $[a; b]$

➡ Видно, что знаки значений функций на концах отрезка противоположные. Именно это условие гарантирует, что на данном отрезке существует как минимум один ноль функции ( корень уравнения $f(x) = 0$ ).

Проверить тот факт, что знаки значений функций на концах отрезка $[a; b]$ противоположные можно через произведение $f(a) cdot f(b)$. Если это произведение меньше $0$, то знаки противоположные, иначе — одинаковые.

Кстати, хочу напомнить формулу, по которой можно найти координату центра отрезка ( $x_c$ ), заданного координатами своих концов ( $x_l$ и $x_r$ ):

Рисунок — формула для нахождения координаты середины отрезка

Сейчас найду середину отрезка $[a; b]$, обозначив его буквой $c$. Также сразу обозначу знак функции в этой точке, то есть знак значения $f(c)$:

Рисунок — нахождение центра отрезка $[a; b]$ и определение знака функции в этой точке

Итак, точка $c$ разбила отрезок $[a; b]$ на два подотрезка: $[a; c]$ и $[c; b]$. Искомый ноль функции лежит на одном из этих подотрезков.

Чтобы отобрать нужный подотрезок ( речь о подотрезке, содержащий искомый корень ), необходимо воспользоваться правилом произведения, о котором писал чуть выше.

Рассмотрим знаки следующих произведений:

➡ Как было ранее доказано, корень лежит на том отрезке, для которого произведение значений функции на концах отрезка меньше $0$. Делаю вывод, что искомый корень принадлежит отрезку $[c; b]$. Визуально это подтверждается. Поэтому последующий анализ перекидывается с отрезка $[a; b]$ на отрезок $[c; b]$.

Сейчас найду середину отрезка $[c; b]$, обозначив его буквой $d$. Также сразу обозначу знак функции в этой точке, то есть знак значения $f(d)$:

Рисунок — нахождение центра отрезка $[c; b]$ и определение знака функции в этой точке

Итак, точка $d$ разбила отрезок $[c; b]$ на два подотрезка: $[c; d]$ и $[d; b]$. Искомый ноль функции лежит на одном из этих подотрезков.

Чтобы отобрать нужный подотрезок ( речь о подотрезке, содержащий искомый корень ), необходимо воспользоваться правилом произведения, о котором писал чуть выше.

Рассмотрим знаки следующих произведений:

➡ Как было ранее доказано, корень лежит на том отрезке, для которого произведение значений функции на концах отрезка меньше $0$. Делаю вывод, что искомый корень принадлежит отрезку $[c; d]$. Визуально это подтверждается. Поэтому последующий анализ перекидывается с отрезка $[c; b]$ на отрезок $[c; d]$.

На каждой итерации длина отрезка, содержащего искомый корень, сокращается вдвое! Именно по этой причине такой метод приближенного нахождения корня называется методом деления отрезка пополам.

Возникает закономерный вопрос: а когда заканчиваются все вычисления?

Очень важно понимать, что значения корня находится приближенно, то есть с некой погрешностью ( в теории программирования это называется точностью расчетов ).

Например, я хочу найти приближенное значение корня с точностью $EPS = 0.001$, то есть с точностью одна тысячная. Это не очень высокая точность, но вполне приемлемая. Это означает, что если значение реального корня уравнения составляет $5.735$, то мое приближенное решение должно находиться на отрезке $[ 5.735 — 0.001; 5.735 + 0.001 ] = [ 5.734; 5.736 ]$.

➡ Поэтому стоит прекратить все вычисления, когда длина отрезка, содержащего искомое значение корня, станет $leq$ заданной точности, то есть $|a — b | leq EPS$, где $a$ и $b$ — значения концов отрезка.

Но есть еще один важный нюанс, который многие упускают из виду. Как было сказано ранее, при выборе подотрезка, на котором находится корень, вычисляются произведения $f(a) cdot f(c)$ и $f(c) cdot f(b)$, где $a$, $b$ — концы текущего отрезка, а $c$ — середина отрезка.

А представим такую ситуацию, что центр отрезка $c$ точно совпал с искомым корнем, то есть $f(c) = 0$. В этом случае оба эти произведения будут равны $0$ и ни одно из условий не выполнится.

Поясню сказанное на следующем графике $f( x ) = x^2 + x — 20$:

Рисунок — график функции $f( x ) = x^2 + x — 20$

Очевидно, что уравнение $x^2 + x — 20$ имеет ровно два целых корня: $-5$ и $4$. Я поработаю с положительным корнем, то есть с корнем $4$ и попробую найти его приближенное значение методом деления отрезка пополам. В качестве стартового отрезка возьму отрезок $[2; 6]$.

Рисунок — поиск корня ( равного $4$ ) на отрезке $[2; 6]$

Координата середины отрезка $[2; 6]$ равна $4$, то есть $c = 4$. Произведение $f(a) cdot f(c) = f(2) cdot f(4) = 0$ и это произведение $f(c) cdot f(b) = f(4) cdot f(6) = 0$.

Оба произведения равны $0$. Разумеется, на практике такая ситуация встречается чрезвычайно редко, так как искомые корни далеки от целых значений. Но тем не менее, такая ситуация может возникнуть и моя программа должна корректно ее обрабатывать.

В примере выше я вышел на корень ( его точное значение, равное $4$ ) на самой первой итерации метода деления отрезка пополам. Но при этом длина отрезка, на котором находится корень, составляет $|b — a| = |6 — 2| = 4$ единицы. Если точность расчетов $EPS = 0.0001$, то метод должен продолжать свою работу, так как все приближенные вычисления по нахождению корня заканчиваются, когда длина подотрезка, содержащего корень, становится $leq$ заданной точности, то есть должно выполниться такое условие: $|b — a| leq EPS$ Да, вот есть такой небольшой неприятный момент в этом методе, на который надо обращать внимание.

➡ Для некоторых нелинейных уравнений метод бисекции не работает, хотя все условия, казалось бы, выполнены.

Рассмотрим функцию $f( x ) = x^2 — 6x + 9$. Графиком этой функции является парабола, которая касается оси абсцисс лишь в одной точке — точке, с координатами $$. Другими словами, уравнение $f( x ) = 0$ имеет два одинаковых корня, равных $3$.

Рисунок — график функции $f( x ) = x^2 — 6x + 9$

Посмотрим, как себя поведет алгоритм, если попытаться найти приближенное значение корня, равного $3$. Например, возьмем стартовый отрезок $[a; b] = [1; 6]$.

Рисунок — стартовый отрезок для нахождения корня от $1$ до $6$

Значение функции в точке $a = 1$ — положительно. Аналогично значение функции в точке $b = 6$ — также положительно. Следовательно, произведение $f( a ) cdot f( b )$ будет также положительным. Алгоритм сделает вывод, что на заданном отрезке нет ни одного корня, хотя по факту это не так!

Важный вывод: если график функции касается оси абсцисс, то классический метод деления отрезка пополам начинает работать некорректно.

В результате я написал программу на языке «чистый» Си в среде программирования Visual Studio $2010$ ( стандарт C89 ), которая находит приближенное значение корня заданного нелинейного уравнения. Программа тщательно прокомментирована и учитывает пограничные случаи.

Источник: www.algograph.ru

Методом деления отрезка пополам

Метод деления отрезка пополам заключается в следующем. Проверяется наличие корня на отрезке [a, b] (рис.3.7).

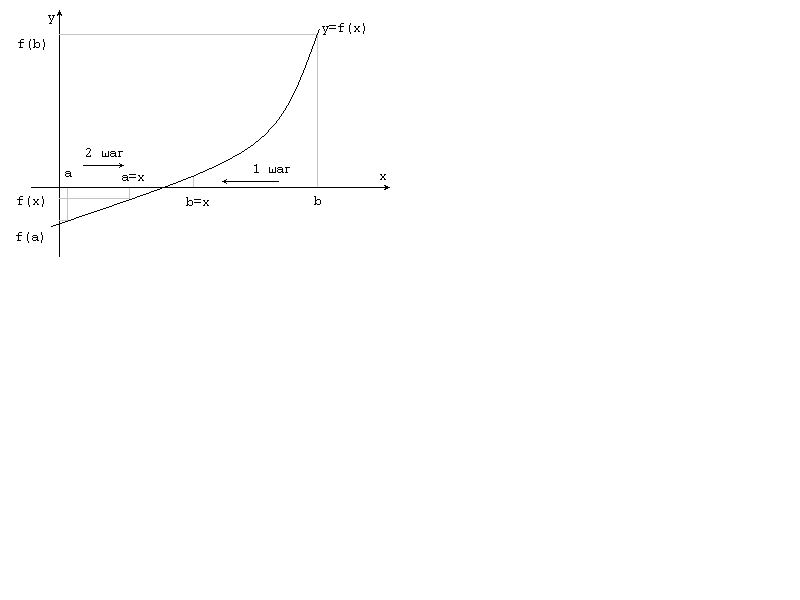
Рис.3.7. Метод деления отрезка пополам.

Для этого вычисляются значения функций f(a) и f(b). Если f(a)*f(b)>0, то уравнение не имеет корней на заданном отрезке. Если f(a)*f(b)1 = f(a). Затем определяем значение x как среднюю точку между а и b, вычисляем значения y₂ = f(x). Теперь, если f(a)*f(x)>0, то корень находится на отрезке [x, b], иначе – на отрезке [a,x].

В соответствии с этим, перемещаем точку а вправо или точку в влево, выполняя, соответственно присваивание а = х илиb=x. Таким образом, получаем второй отрезок [a, b], но вдвое меньший предыдущего. Процесс деления отрезка пополам продолжаем до тех пор, пока отрезок [a, b] не станет меньше заданной точности. После этого вычисляем значение x = (a+b)/2.

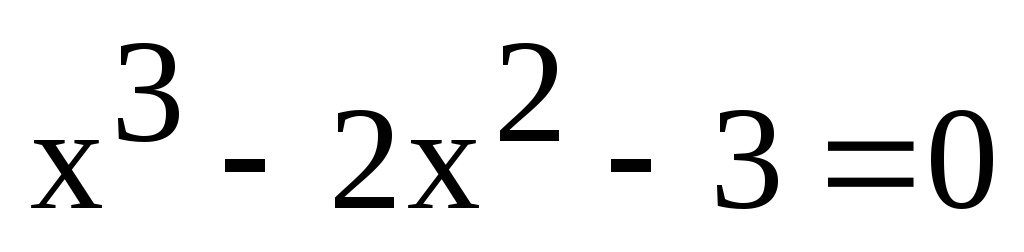
Пример 3.7. Решение уравненияс заданной точностью= 0.01методом деления отрезка пополам, если корень находится на отрезке[1,3].

float x, a = 1, b = 3, y1, y2, eps = 0.001, e, r, l;

y1 = a*a*a – 2*a*a – 3;

y2 = b*b*b – 2*b*b – 3;

y1 = a*a*a – 2*a*a – 3;

y2 = x*x*x – 2*x*x – 3;

Контрольные вопросы

1. Каким образом цикл while может имитировать циклfor?
2. Каким образом цикл while может имитировать циклdo-while?
3. В каких случаях используются операторы break, continue, exit?
4. Почему в языке С++ нет необходимости использовать оператор goto?

Лабораторное задание 1. Для своего варианта cоставить схему алгоритма и программу вычисления суммы бесконечного ряда c точностью, значение которой ввести с клавиатуры задание 1. 2. Решить указанные в задании уравнения согласно номеру своего варианта двумя методами и сравнить эти методы по точности и количеству шагов. 3. В процессе выполнения лабораторного задания использовать средства отладки языка Borland C++.

Порядок выполнения лабораторной работы 1. При подготовке к лабораторной работе ознакомиться с данным описанием и составить три программы, указанные в лабораторном задании. 2. Подготовить файлы с программами вычисления суммы и решения уравнений и отладить их. Результаты показать преподавателю. 3. Оформить отчет. Требования к отчету Отчет должен содержать:

1. название и цель работы;
2. схему алгоритма;
3. краткие теоретические сведения;
4. текст программы для варианта задания, соответствующего номеру фамилии студента в группе (если студент закреплен за определенной ЭВМ, то номеру ЭВМ);
5. результаты выполнения программ.

Варианты заданий Задание 1 Ввести с клавиатуры х и точность вычисления Eps. Вычислить с заданной точностью сумму

Номер варианта	Задание
1, 16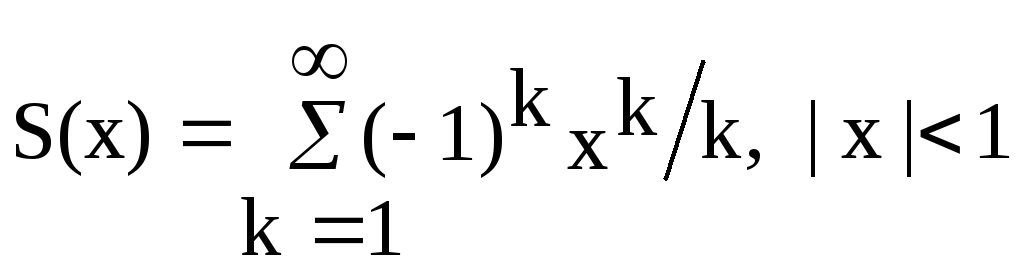
2, 17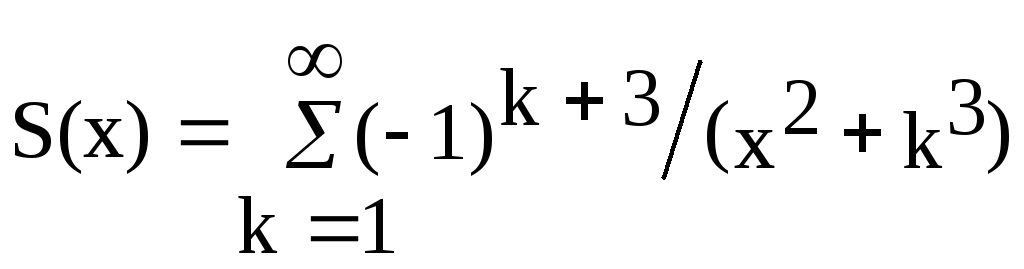
3, 18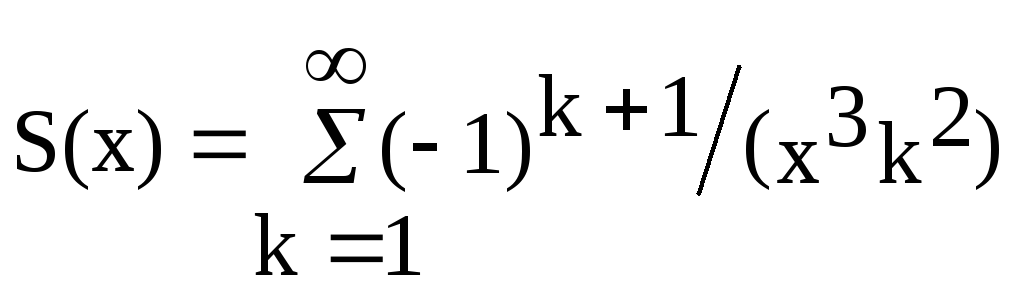
4, 19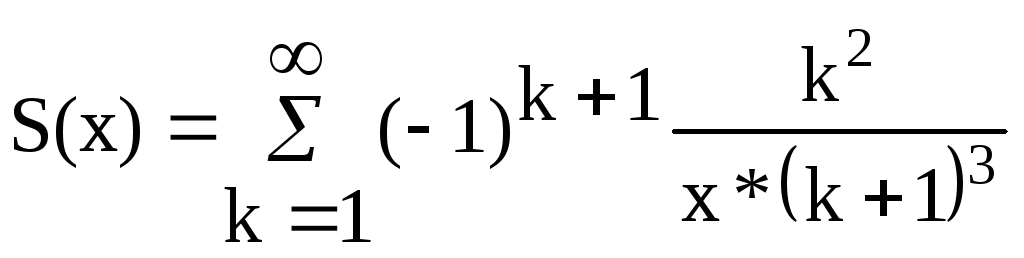
5, 20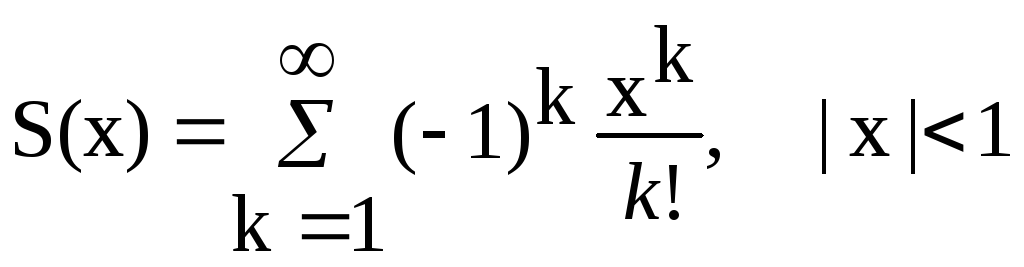
6, 21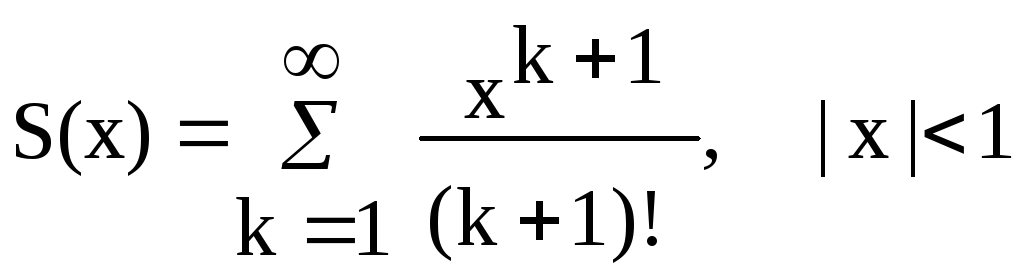
7, 22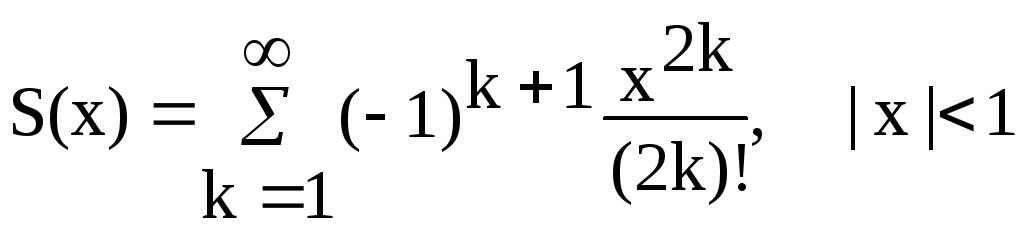
8, 23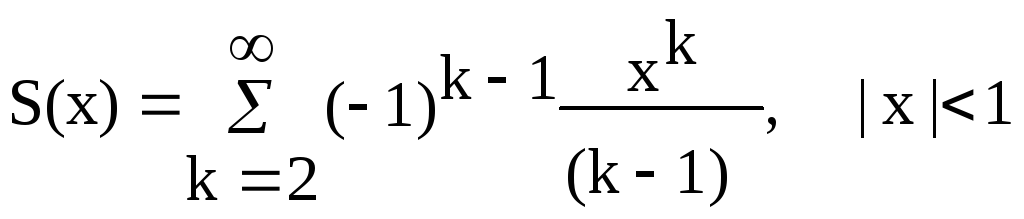
Номер варианта	Задание
9, 24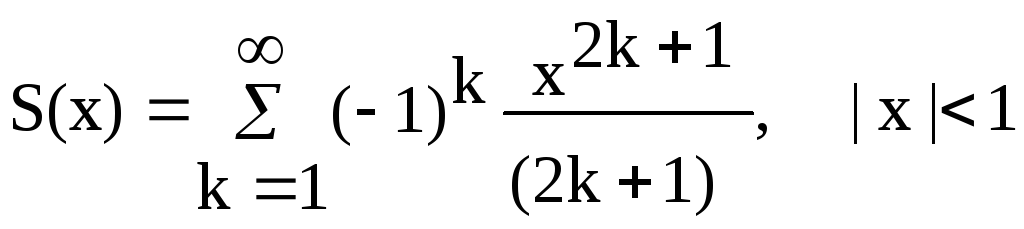
10, 25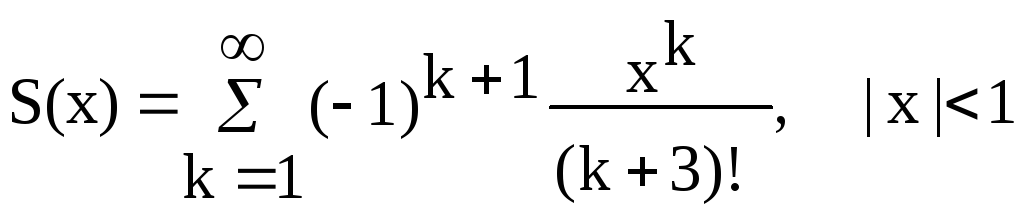
11, 26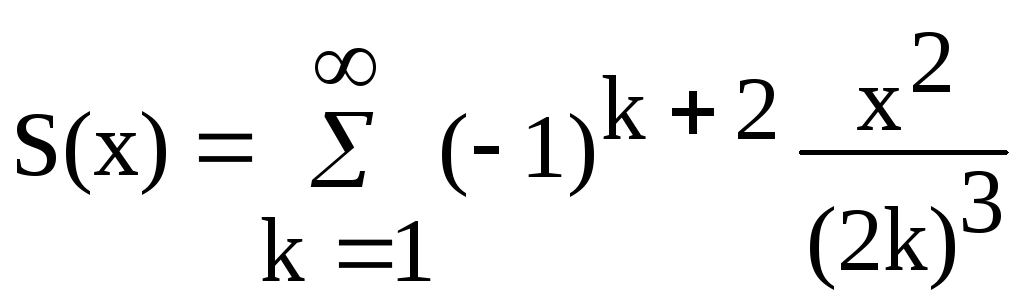
12, 27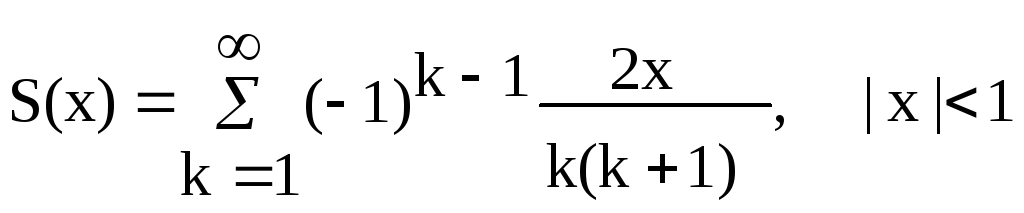
13, 28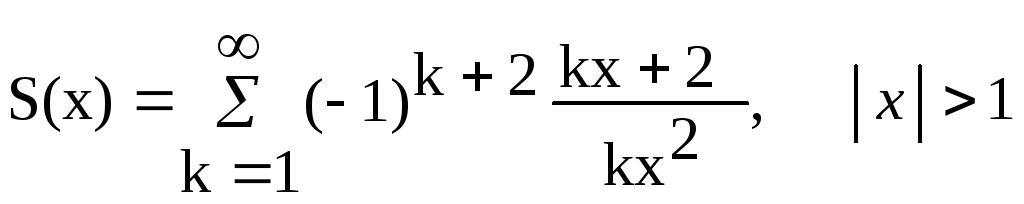
14, 29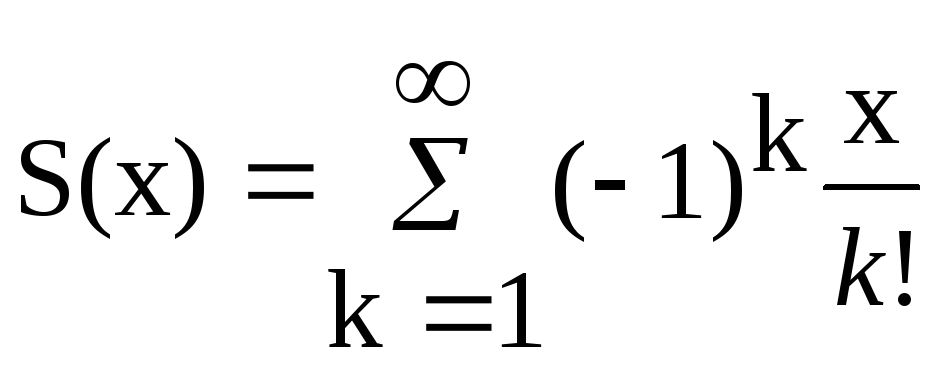
15, 30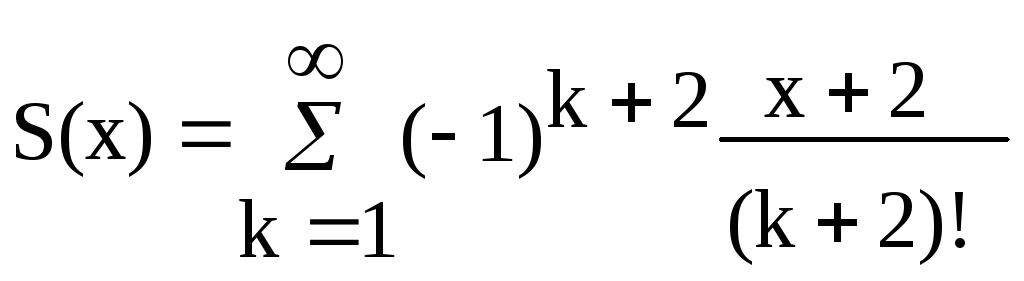

Источник: studfile.net

Метод деления отрезка пополам

Метод бисекции или метод деления отрезка пополам – простой численный метод для решения нелинейного уравнения вида f(x) = 0.

Описание алгоритма

Метод применим для численного решения уравнения f(x) = 0 для действительной переменной x, где f(x) – непрерывная функция, определенная на интервале [a, b], а f(a) и f(b) имеют противоположные знаки. В этом случае говорят, что a и b заключают в скобки корень, поскольку по теореме о промежуточном значении непрерывная функция f(x) должна иметь хотя бы один корень в интервале (a, b).

На каждом шаге метод делит интервал на две части, вычисляя среднюю точку t = (a + b) / 2 интервала и значение функции f(t) в этой точке. Если только t не является корнем (что очень маловероятно, но возможно), теперь есть только две возможности: либо f(a) и f(t) имеют противоположные знаки и скобки для корня, либо f(t) и f(b) иметь противоположные знаки и заключать в скобки корень. Метод выбирает подинтервал, который гарантированно будет скобкой, в качестве нового интервала, который будет использоваться на следующем шаге. Таким образом, интервал, содержащий ноль f(x), уменьшается по ширине на 50% на каждом шаге. Процесс продолжается до тех пор, пока интервал не станет достаточно малым.

Если f(a) и f(t) имеют противоположные знаки, тогда метод устанавливает t как новое значение для b, а если f(b) и f(t) имеют противоположные знаки, то метод устанавливает t как новое значение а. Если f(t) = 0, то t может быть принято как решение, и процесс останавливается. В обоих случаях новые f(a) и f(b) имеют противоположные знаки, поэтому метод применим к этому меньшему интервалу.

Реализация алгоритма

using System; class Program < /// /// Модуль числа ///  /// Число  /// Абсолютное значение числа  static double Abs(double x) < return (x < ) ? -x : x; > /// /// Знак числа ///  /// Число  /// -1 если число отрицательное, 1 - если положительное  static int Sign(double x) < return (x < ) ? -1 : 1; > /// /// Метод бисекции(деления отрезка пополам) ///  /// Функция  /// Начало отрезка  /// Конец отрезка  /// Точность вычислений  ///  static double BisectionMethod(Funcdouble, double> function, double a, double b, double precision = 1e-10) < while (true) < var t = (a + b) / 2; if (function(t) == 0.0 || Abs(b - a) < Abs(precision)) < return t; > if (Sign(function(t)) == Sign(function(a))) < a = t; >else < b = t; >> > static void Main(string[] args) < //локальная функция double f(double x) => 3 * Math.Pow(x, 2) - 6 * x + 1; Console.WriteLine("Метод бисекции для функции 3x^2 - 6x + 1"); Console.Write("Введите начало отрезка: "); var a = double.Parse(Console.ReadLine()); Console.Write("Введите конец отрезка: "); var b = double.Parse(Console.ReadLine()); Console.Write("Введите точность вычислений: "); var eps = double.Parse(Console.ReadLine()); var result = BisectionMethod(f, a, b, eps); Console.WriteLine("x ="" rnf() ="" ", result, f(result)); Console.WriteLine("Для выхода нажмите клавишу Enter. "); Console.ReadKey(); > > 

Метод можно применять к любой функции f(x)=0, для этого достаточно изменить локальный метод double f(double x) в коде программы.

Источник: programm.top

>»>