Use saved searches to filter your results more quickly
Cancel Create saved search
You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window.
Reload to refresh your session.
Приложение, решающее задачу Линейного Программирования симплекс методом, графическим методом и методом искусственного базиса.
overcomzi/simplex_method
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
Switch branches/tags
Branches Tags
Could not load branches
Nothing to show
Could not load tags
Nothing to show
Name already in use
A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?
Cancel Create
- Local
- Codespaces
HTTPS GitHub CLI
Use Git or checkout with SVN using the web URL.
Work fast with our official CLI. Learn more about the CLI.
Урок 3. Решение задачи симплекс-методом. Для тех, кто не разобрался с алгоритмом симплекс-метода.
Sign In Required
Please sign in to use Codespaces.
Launching GitHub Desktop
If nothing happens, download GitHub Desktop and try again.
Launching GitHub Desktop
If nothing happens, download GitHub Desktop and try again.
Launching Xcode
If nothing happens, download Xcode and try again.
Launching Visual Studio Code
Your codespace will open once ready.
There was a problem preparing your codespace, please try again.
Latest commit
cad3adc Oct 7, 2021
Git stats
Files
Failed to load latest commit information.
Latest commit message
Commit time
README.md
Приложение, которое решает задачу Линейного Программирования графическим и симплекс методом
Задача линейного программирования (ЛП) – это задача, в которой требуется найти максимум или минимум функции, называемой целевой функцией, при ограничениях, заданных системой линейных неравенств или уравнений.

Пример такой системы (ЛП):
Приложене реализует 3 способа решения:
- Симплекс метод
- Метод искусственного базиса
- Графический метод
- Приложения отображает каждый промежуточный результат. Если нужен ответ, то достаточно нажать кнопку «Получить ответ»
- Имеется история промежуточных результатов, поэтому легко откатиться назад
- Можно загружать и выгружать условия задачи
Файл -> Открыть / Сохранить условие задачи - Отображение чисел можно представить в виде обыкновенных (1/2) или десятичных (0.5) дробей
- Есть возможность выбирать базисный вектор самостоятельно на каждом этапе решения
About
Приложение, решающее задачу Линейного Программирования симплекс методом, графическим методом и методом искусственного базиса.
Cимплексный метод решения задачи линейного программирования (ЗЛП)
Источник: github.com
Симплекс-метод для Windows
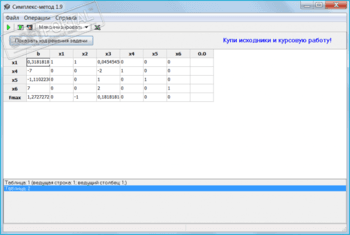
Симплекс-метод — программа для решения задач линейного программирования симплекс-методом. Это приложение приводит задачу к каноническому виду и производит ее итеративное решение с помощью пересчета симплекс-таблицы. При этом выводится подробный отчет о ходе решения задачи. Всего имеется три режима решения задач: автоматический, пошаговый, ручной.
В автоматическом режиме инструмент сам выбирает разрешающий столбец и строку, которые обеспечивают максимальное возрастание или уменьшение целевой функции, а также автоматически пересчитывает все таблицы. В пошаговом режиме каждая пересчитанная таблица выводится на экран, что удобно для просмотра промежуточных результатов решения задачи. В этом режиме разрешающий столбец и строку программа также выбирает сама. В ручном режиме пользователь сам выбирает разрешающую строку и столбец. Есть возможность экспорта в Excel всех таблиц, полученных в ходе решения задачи.
ТОП-сегодня раздела «Математика»
![]()
MathType 7.4.8.0 MathType — отличное приложение для работы с формулами, математическими выражениями и.
Advanced Grapher 2.2 Advanced Grapher — Мощная и простая в использовании программа для построения графиков и их анализа.
Satellite Antenna Alignment 4.0 Satellite Antenna Alignment — Программа предназначена для расчета углов, необходимых при установке.
SMath Studio 0.99 build 6671 SMath Studio — бесплатная программа для вычисления математических выражений и построения.

Отличник 3.38 Отличник — тренажер решения заданий по математике и русскому языку для учащихся 1-4.
![]()
GeoGebra 6.0.779 GeoGebra — графический калькулятор для функций, геометрии и статистики. Здесь объединены.
Отзывы о программе Симплекс-метод
Феликс про Симплекс-метод 1.9 [08-03-2017] Программа не всегда даёт правильный результат.
3*x1 + 1*x2 + 1*x3 + 0*x4 = 15
2*x1 + 0*x2 + 1*x3 + 1*x4 = 11
F(x) = 4*x1 — 1*x2 + 2*x3 + 0*x4 -> max
Получаем
x1 = 5
x2 = 0
x3 = 0
x4 = 1
Значение целевой функции: Fmax = 20
Правильный ответ: Fmax = 22
Результат получен в программе Sim.exe (Softodrom)
3 | 16 | Ответить
Источник: www.softportal.com
Онлайн Калькулятор: Симплекс Метод
 English
English Русский
Русский



Мобильное приложение: Симплекс Метод

Решай задачи линейного программирования в режиме offline — без доступа к интернету!
![]()
![]()
Введите значения целевой функции:
objective function input select of objective function
objective function input select of objective function
objective function input select of objective function
objective function input select of objective function
system of constraints input
system of constraints input
system of constraints input
system of constraints input
select system of constraints
system of constraints input
system of constraints input
system of constraints input
system of constraints input
system of constraints input
select system of constraints
system of constraints input
system of constraints input
system of constraints input
system of constraints input
system of constraints input
select system of constraints
system of constraints input
system of constraints input
system of constraints input
system of constraints input
system of constraints input
select system of constraints
system of constraints input
Пример решения
F(x) = 3×1 + 4×2 → max
| 000 | 2×1 + x2 ≤ 600 |
| 0x1 + 0x2 ≤ 225 | |
| 5×1 +4×2 ≤ 1000 | |
| 2×2 ≥ 150 | |
| 0x1 + 0x2 ≥ 0 |
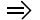
F(x) = 3×1 + 4×2 + 0x3 + 0x4 + 0x5 + 0x6 + 0x7 — Mx8 — Mx9 → max
| 000 | 2×1 + x2 + x3 = 600 |
| + x4 = 225 | |
| 5×1 + 4×2 + x5 = 1000 | |
| 2×2 — x6 + x8 = 150 | |
| — x7 + x9 = 0 |
Предварительный этап:
Предварительный этап начинается с того что необходимо избавиться от отрицательных значений(если таковые имеются) в правой части ограничений. Для чего соответствующие ограничения умножаем на -1. После данной манипуляции знак неравенства меняем на противоположный.
Далее необходимо избавиться от неравенств, для чего в левую часть неравенств вводим компенсирующие переменные. Если неравенство вида ≤, то компенсирующая переменная имеет знак +, если неравенство вида ≥, то компенсирующая переменная имеет знак -. Компенсирующие переменные входят в целевую функцию задачи с нулевым коэффициентом.
Теперь в системе ограничений необходимо найти достаточное количество базисных переменных. В каждом ограничении должна быть одна базисная переменная. Базисной является переменная, которая имеет при себе коэффициент 1 и встречается только в одном ограничении. Если в каком-то ограничении нет базисных переменных, то добавляем их искусственно, причем искусственные переменные входят в целевую функцию с коэффициентом -M, если целевая функция стремится к мах и с М, если целевая функция стремится к min.
| B | Cb | P | x1 | x2↓ | x3 | x4 | x5 | x6 | x7 | x8 | x9 | Q |
| 3 | 4 | -M | -M | |||||||||
| x3 | 600 | 2 | 1 | 1 | 600 | |||||||
| x4 | 225 | 1 | ∞ | |||||||||
| x5 | 1000 | 5 | 4 | 1 | 250 | |||||||
| x8 ← |
-M | 150 | 2 | -1 | 1 | 75 | ||||||
| x9 | -M | -1 | 1 | ∞ | ||||||||
| max | -150M | -3 | -2M-4 | M | M | |||||||
Вычисление элементов таблицы:
Элементы колонки базис(B)
Переносим в таблицу базовые элементы, которые мы определили на предварительном этапе:
Элементы колонки Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Значения упрявляемых переменных и колонки P
На данном этапе никаких вычислений не нужно, просто переносим значения из предварительного этапа в соответствующие ячейки таблицы:
Источник: linprog.com