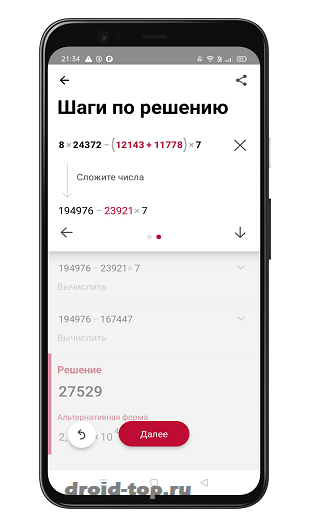
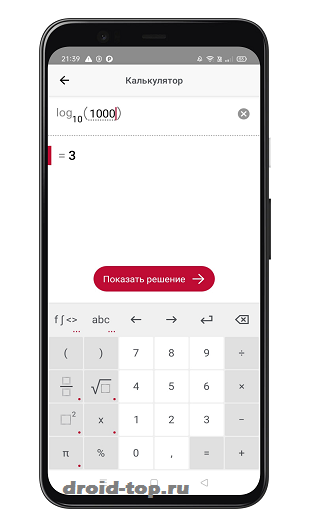
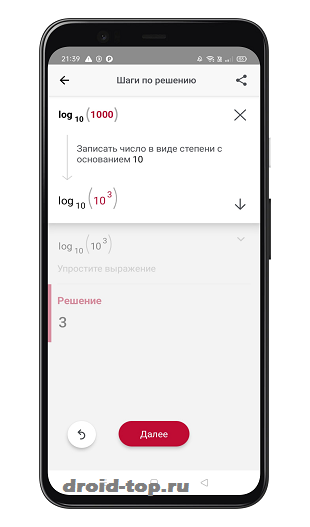
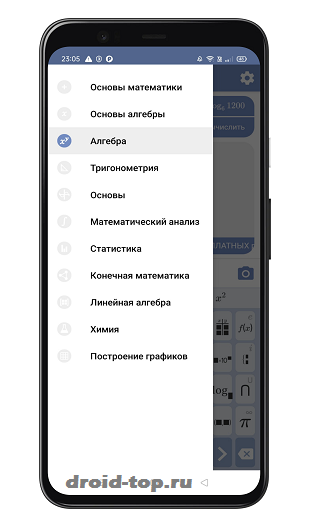
Цель работы: приобретение навыков разработки параллельных программ с использованием OpenMP.
Задание
Разработать последовательную и параллельную программы решения СЛАУ матричным методом. Сравнить время работы последовательной и параллельной программ.
Решение системы линейных алгебраических уравнений матричным методом определяется по формуле:
– обратная матрица коэффициентов переменных,
– матрица-столбец свободных членов,
– матрица-столбец неизвестных переменных.
Основной задачей в данном методе является вычисление обратной матрицы, зная её, вычислить неизвестные переменные не займет много времени.
В данной работе для поиска обратной матрицы использовались элементарные преобразования матрицы, которые применяются в методе Гаусса решения СЛАУ, таким образом, матрица вида (A|E) приводится к матрице вида (E|
), где E – единичная матрица. То есть все те преобразования, которые совершаются над матрицей A, совершаются и над матрицей E. Таким образом, матрица A превратится в единичную, а единичная превратится в матрицу обратную A.
Решение алгебраических уравнений
Описание метода на примерах:
Пример 1. Решить СЛАУ из 3х уравнений:
;
1 шаг. Составляется матрица коэффициентов неизвестных переменных (A), матрица-столбец свободных членов (B) и единичная матрица (E):
;
Теперь необходимо привести матрицу A к верхнетреугольному виду, где элементы на главной диагонали равны 1, а элементы ниже главной диагонали равны 0.
2 шаг.
Для начала, если элемент на главной диагонали равен нулю, то необходимо найти строку, где элемент этого же столбца не был равен нулю и поменять местами строки. Если такую строку найти не удалось, то обратная матрица не может быть найдена, как и решение СЛАУ. В данном примере в 1 строке на главной диагонали стоит число 1, значит менять её местами с какой-либо другой строкой не нужно.
Теперь необходимо разделить каждый элемент текущей строки на элемент, находящийся на главной диагонали, чтобы элемент на главной диагонали стал равен единице. Так как в данном примере элемент уже равен 1, то исходный вид матриц A и E не изменится.
Далее элементы, находящиеся в столбце под элементом главной диагонали необходимо занулить. Так как на 3м шаге мы превратили элемент на главной диагонали в 1, то из каждой следующей строки можно отнять предыдущую строку, умноженную на элемент 1-го столбца этой строки, таким образом, элемент находящийся в столбце под элементом главной диагонали занулится (например, 7 * 1 – 7 = 0). В данном примере:
После зануления элемента 2й строки:
;
После зануления элемента 3й строки:
;
Далее повторяются шаги 2-4 для следующих строк, пока матрица A не примет верхнетреугольный вид.
Делим элементы 2 строки на элемент, находящийся на главной диагонали (на 6):
;
Отнимаем от 3-й строки 2ю, умноженную на единицу:
;
Делим элементы 3й строки на -2,33:
5 шаг.
Далее происходит обратный ход. Необходимо занулить элементы, находящиеся выше главной диагонали. Алгоритм зануления тот же, что и в прямом ходе, только обход матрицы происходит снизу вверх.
Зануление элемента 2-й строки столбца:
Зануление элемента 3-й строки столбца:
;
Так как элемент 1 строки, находящийся над элементом главной диагонали во 2м столбце уже равен нулю, то занулять его не нужно.
Таким образом, мы превратили матрицу A в единичную, а единичную в обратную матрицу A, отсюда:
.
Осталось только найти решение СЛАУ умножив обратную матрицу на столбце свободных членов:
Программы тестировались на СЛАУ из 200 уравнений. Для начала было вычислено среднее время выполнения последовательной программы (рис.1):
Рисунок 1 – результат выполнения последовательной программы
Среднее время выполнения последовательной программы равно 16,2с.
Далее было принято решение распараллелить зануление элементов, лежащих ниже главной диагонали в процессе прямого хода (листинг 1.1) и зануление элементов, лежащих выше главной диагонали в процессе обратного хода (листинг 1.2).
Листинг 1.1. Распараллеленный цикл зануления элементов в процессе прямого хода:
#pragma omp parallel < #pragma omp for for (int i = k + 1; i < size; i++) < double multi = matrix[i][k]; for (int j = 0; j < size; j++) < matrix[i][j] -= multi * matrix[k][j]; E[i][j] -= multi * E[k][j]; >> >
Листинг 1.2. Распараллеленный цикл зануления элементов в процессе обратного хода:
#pragma omp parallel < #pragma omp for for (int i = k — 1; i >-1; i—) < double multi = matrix[i][k]; for (int j = 0; j < size; j++) < matrix[i][j] -= multi * matrix[k][j]; E[i][j] -= multi * E[k][j]; >> >
Среднее время выполнения при этом уменьшилось на 12,1 с. и стало равно 4,1 с.
Далее распараллеливается цикл вычисления неизвестных переменных X (листинг 1.3):
Листинг 1.3. Распараллеленный цикл вычисления неизвестных переменных
#pragma omp parallel < #pragma omp for for (int i = 0; i < equations_amount; i++) < X[i] = 0; for (int j = 0; j < equations_amount; j++) X[i] += matrix[i][j] * B[j]; >>
Среднее время выполнения программы уменьшилось на 0,15 с. и стало равно 3,95 с.
Далее распараллеливается цикл деления каждого элемента строки на элемент этой же строки, лежащий на главной диагонали матрицы (листинг 1.4):
Листинг 1.4. Распараллеленный цикл деления элементов
double div = matrix[k][k]; #pragma omp parallel < #pragma omp for for (int j = 0; j < size; j++) < matrix[k][j] /= div; E[k][j] /= div; >>
Среднее время выполнения программы уменьшилось на 0,05 с. и стало равно 3,9 с (рис.2).
Рисунок 2 – результат выполнения параллельной программы
В данной работе коэффициенты переменных и свободные члены генерируются автоматически. Эти числа могут принимать значения от 0 до 100.
Как видно из рисунков 1-4 и таблицы 1, время выполнения параллельной программы меньше времени выполнения последовательной программы в 4 раза. В процессе выполнения параллельной программы все ядра процессора загружены на 100%.
Исходный код параллельной программы представлен в листинге 2. Параллельная программа отличается от последовательной только наличием директив #pragma omp parallel и #pragma omp for. Распараллеливание других циклов или создание параллельных областей либо невозможно, либо не приведет к уменьшению времени выполнения программы
Листинг 2: исходный код параллельной программы:
#include #include #include #include using namespace std; bool search_reverse_matrix(vector > int size = matrix.size(); vector > E(size, vector(size)); //Заполнение единичной матрицы for (int i = 0; i < size; i++) < for (int j = 0; j < size; j++) < if (i == j) E[i][j] = 1.0; else E[i][j] = 0.0; >> //Трансформация исходной матрицы в верхнетреугольную for (int k = 0; k < size; k++) < if (abs(matrix[k][k]) < 1e-8) < bool changed = false; for (int i = k + 1; i < size; i++) < if (abs(matrix[i][k]) >1e-8) < swap(matrix[k], matrix[i]); swap(E[k], E[i]); changed = true; break; >> if (!changed) return false; > double div = matrix[k][k]; #pragma omp parallel < #pragma omp for for (int j = 0; j < size; j++) < matrix[k][j] /= div; E[k][j] /= div; >> #pragma omp parallel < #pragma omp for for (int i = k + 1; i < size; i++) < double multi = matrix[i][k]; for (int j = 0; j < size; j++) < matrix[i][j] -= multi * matrix[k][j]; E[i][j] -= multi * E[k][j]; >> > > //Формирование единичной матрицы из исходной //и обратной из единичной for (int k = size — 1; k > 0; k—) < #pragma omp parallel < #pragma omp for for (int i = k — 1; i >-1; i—) < double multi = matrix[i][k]; for (int j = 0; j < size; j++) < matrix[i][j] -= multi * matrix[k][j]; E[i][j] -= multi * E[k][j]; >> > > matrix = E; return true; > double random(const int min, const int max) < if (min == max) return min; return min + rand() % (max — min); >int main() < setlocale(LC_ALL, «RUS»); int equations_amount; cout > equations_amount; vector> matrix(equations_amount, vector(equations_amount)); vector B(equations_amount); // Заполняем матрицу коэффициентов и B for (int i = 0; i < equations_amount; i++) < for (int j = 0; j < equations_amount; j++) matrix[i][j] = random(0, 100); B[i] = random(0, 100); >// Вывод системы уравнений /*cout = 0) cout cout */ double t = clock(); // Вычисление обратной матрицы if (!search_reverse_matrix(matrix)) < cout // Матрица-столбец неизвестных X и вычисление окончательного результата vector X(equations_amount); #pragma omp parallel < #pragma omp for for (int i = 0; i < equations_amount; i++) < X[i] = 0; for (int j = 0; j < equations_amount; j++) X[i] += matrix[i][j] * B[j]; >> // Вывод окончательного результата /*cout
В данной лабораторной работе были приобретены навыки разработки параллельных программ с использованием OpenMP. Использование параллельных программ позволяет рационально распределить нагрузку на процессор, что значительно сокращает время выполнения программ. В данной работе время решения одной и той же СЛАУ матричным методом различается в 4 раза.
Источник: codeby.net
Программа для решения алгебраических уравнений
Приложения для решения математики: ТОП-7 лучших на 2022 год
Математика – интересная наука, которую уважают и ненавидят. Если говорить о том, как наука применяется в жизни, то человек использует ее повседневно. Числа представлены на циферблате хронометров, в расписании движения транспорта, уроков и пр. Чтобы научиться работать с цифрами, облегчить повседневные цели, можно использовать приложения для решения математики. Представляем семь лучших прог для устройств, базирующихся на ОС Android и iOS.
ТОП-7 лучших приложения для решения математики
1. Photomath
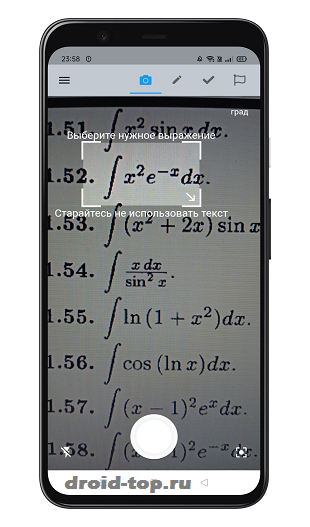
Приложение представлено несложными инструментами. Это камера-калькулятор, который работает посредством модуля на мобильной технике или планшетном компьютере. Посредством софта можно решить простую и сложную задачу, например, квадратное уравнение, логарифм, задачи по тригонометрии, примеры с корнями, степенью и многое другое.
Сильная сторона приложения предоставляет решение задач – это актуально для школьников, студентов, родителей, поверяющих домашнее задание.
- Автоматический запуск камеры;
- Интеллектуальная система решения задач;
- История, сохраняющая десять последних примеров;
- Поддержка устройств на Android и iOS.
2. Geometryx
Программное обеспечение для оперативного расчёта задач по геометрии. Программа высчитывает площадь, периметр, центр тяжести, высоту и другие параметры. Инструмент позиционируется как калькулятор, работающий на базе элементарных теорем. Он работает без лишних действий со стороны пользователя – он быстро выполняет вычисления.
В целом, Geometryx – неплохое приложение для решения примеров по математике с понятным и удобным интерфейсом. Полезно для школьников и студентов, нуждающихся в помощи. Ресурсы приложения помогают справляться со сложными геометрическими задачами и делают предмет более простым.
3. Mathpix
Еще одно приложение для решения математики по фото, способное распознавать рукописный ввод. Продукт разработан для школьников старших классов, студентов высших учебных заведений, преподавателей. В рамках расширенного функционала можно решить:
- Уравнения с дробями;
- Квадратные уравнения;
- Корни и интегралы;
- Производные и многое другое.
Как показывает опыт пользователей, софт на отлично справляется с задачами средней сложности. Разработчик регулярно улучшает продукт, внедряя новые возможности.
4. MalMath
Универсальное приложение для решения задач по математике со следующими особенностями:
- Весь функционал доступен бесплатно;
- Минимальное количество рекламы;
- Может работать без подключения к интернету;
- Подходит для зрелой аудитории, включая учащихся старших классов и ВУЗов, преподавателей;
- Решает примеры с интегралами, производными, логарифмами.
Софт распознает рукописный ввод. Распознавания информации по фото не предусмотрено. Программа переведена на русский язык, может похвастаться красивым, спокойным оформлением, удобно сформированным меню.
5. MyScript Calculator
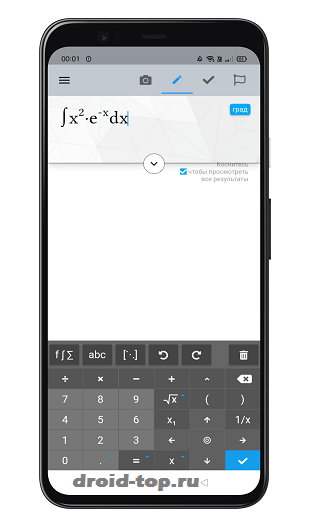
Приложение для решения математики для Андроид, созданное в 2013 году. Многим отличается от классического калькулятора. Фишка программы заключается в распознавании рукописных данных.
Управление не обременено кнопками – перед юзером открывается полотно на весь экран. Задачу для решения вводят стилусом или пальцем. Для удобства использования софта разработчик рекомендует применять планшет или смартфон с большим экраном.
Интеллектуальная система распознает информацию, переводит ее в цифровой формат и выдает результат. Алгоритм способен распознавать цифры и буквы, написанные любым подчерком. Для удобства реализована опция отмены, 100% очистки полотна.
6. Mathematics
Калькулятор с расширенным функционалом, подходящий для учёбы и работы. Строит графики, решает корни, степени, чертит графики. Особенно хорошо дела у проги обстоят с функциями. За несколько секунд автоматизированная система выполнит расчёты, покажет значения на графике. Присутствует функция перевода единиц измерения, например, градусы Цельсия в Фаренгейта, метры в километры и пр.
7. Mathway
Востребованное приложение для решения математики, относящееся к категории универсальных. Может работать с несложными школьными примерами и выполнять вычисления высшей математики. Подходит для тех, кто учит алгебру, тригонометрию.
Программа оснащена приятным интерфейсом с простым меню. Дизайн софта чем-то напоминает классический мессенджер. С помощью онлайн чата вводят условие задачи, робот решает ее и присылает ответ. Задачи решают пошагово – пользователь получает развёрнутый ответ на каждом их этапов.
Mathway поддерживает распознавание текста по фото. Эта опция находится в стадии бета-тестирования, но уже в скором времени разработчик обещает довести ее до идеала.
В скрытом меню доступно несколько разделов, включая алгебру, химию, тригонометрию и другое. Кроме этого, реализован калькулятор с расширенными возможностями.
Программы для решения уравнений
Мощная программа поможет решить линейные и нелинейные уравнения. Интерфейс предполагает отображение всех этапов по шагам. Осуществляет поиск самого рационального способа.
Интересная версия софта, решающего большинство типов несложных примеров. Быстро проводит вычисление и дает окончательный ответ.
Отличная программа для решения уравнений по методу гаусса и крамера. В основе лежит система тригонометрических функций и построение графика по исходным данным.
Полезный инструмент, оснащенный встроенным калькулятором. Выполняет численные расчеты сложных алгебраических выражений, включая: корень, степень, дроби, матрицу и определитель.
Универсальное средство, способное решать задания любой сложности в автоматическом режиме: обыкновенные, логарифмические и дифференциальные уравнения с двумя и тремя неизвестными.
Небольшая утилита справляется с задачами программирования через математические модели. Высокая точность полученного результата. Достаточно нажать на кнопку “Произвести расчет”.
Предполагаемая схема решения логического уравнения сводится к последовательному упрощению действий. В итоге пользователь сможет параллельно изучить материал.
Хороший решатель уравнений с пояснениями. Работает с дробными числами. Подойдет для использования студентам, школьникам старших классов, всем кто любит алгебру, геометрию и математику в целом.
Скачать программы для решения уравнений бесплатно на русском языке. Совместимы с Windows 7, 8, 8.1, 10, XP (64 bit, 32 bit) и доступны без регистрации, смс и вирусов.
Лучшие приложения для решения математики, алгебры, геометрии: ТОП-8 на 2022 год
Подборка приложений для решения задач по математике. Скачиваете бесплатно на Андроид телефон, и они решают за вас линейные уравнения, алгебру, примеры, логарифмы, геометрические задачи и др. Наведите камеру смартфона на уравнение и получите ответ.
Photomath
Мне нравится 14
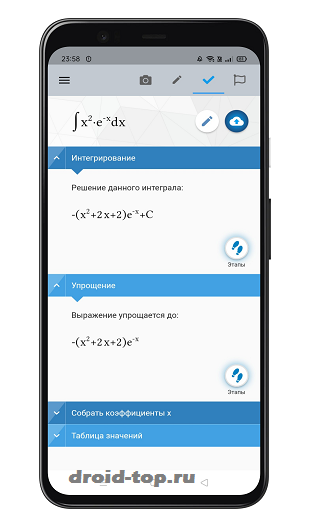
Не только решает математические задачи и формулы, но и обучает, как их решать. Показывает правильную последовательность решения, поясняя действия. Приложение полезно ученикам, родителям и учителям.
- Решение по фото.
- Несколько вариантов решения.
- Инструкции с анимацией.
- Разбитие решения на последовательность шагов для понимания.
Решает базовые математические уравнения, дроби, корни, линейные и квадратные уравнения, логарифмы, функции, тождества, функции, векторы, интегралы, факториалы и многое другое.
Mathway
Наиболее многофункциональное приложение по количеству задач. К сожалению, некоторые функции платные, например, последовательность решения. Но вычисляет математические примеры оно бесплатно.
- Базовая математика
- Тригонометрия
- Алгебра
- Анализ
- Химия
- Построение графиков
- Статистика
Microsoft Math Solver
Удобная программа для андроид, чтобы решать логарифмы, алгебраические формулы, математические уравнения, примеры, задачи и много другого. Алгоритм быстро распознаёт задание и выводит пошаговое решение с дополнительными материалами по теме.
- Сфотографируйте уравнение и получите ответ.
- Можно написать на экране пример и приложение его решит.
- Распознаёт машинный и письменный текст.
- Показывает подробные шаги решения с объяснениями.
- Встроенная озвучка текста.
- Подбирает тематические контент для обучения (видео из ютуб, статьи, конспекты и др.).
- Проводит викторины среди пользователей с выставлением результатов.
Maple Калькулятор
Функциональный софт для решения простых и сложных математических заданий на андроид телефоне. Имеет приличный дизайн интерфейса и функцию распознавания примеров по фото. Ответы выдаёт с подробными шагами по решению.
- Подойдёт не только для поиска ответа, но и для пошагового изучения, как решить пример.
- Базовая математика, алгебра, дифференциальные уравнения, анализ и др.
- Может распознать машинописный и рукописный текст.
- Решает множество видов задач.
- Строит графики.
- Сообщество Maple Learn, в котором можно поделиться результатами и найти ошибки.
Camera Math
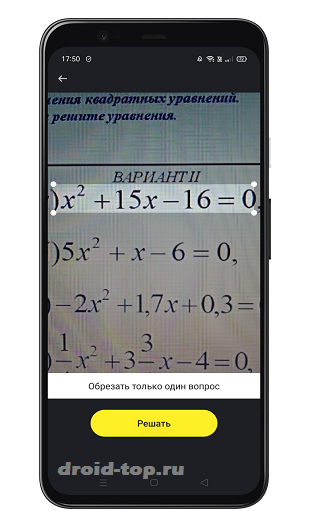
Как заявляют разработчики, приложение может распознать не только пример, но и вопрос задачи. Как я понял, эта функция работает не со всеми условиями. Например, я сканировал задачу на время, дистанцию и скорость. Оно выдало в ответ вычисление корня из цифр, упоминающихся в тексте. В остальном программа справляется отлично, даже самостоятельно обрезает края фото, выделяя нужное уравнение.
- Сфотографируйте, что нужно решить и ждите ответ.
- Если программа не может справиться с задачей, спросите решение у репетиторов (в платной версии).
- Тригонометрия, алгебра, начальная математика, исчисления, статистика, геометрия и др.
- Подробные шаги решения (в премиум подписке).
- Несколько способов решения.
Источник: al-shell.ru
1. Решение систем линейных алгебраических уравнений (слау)
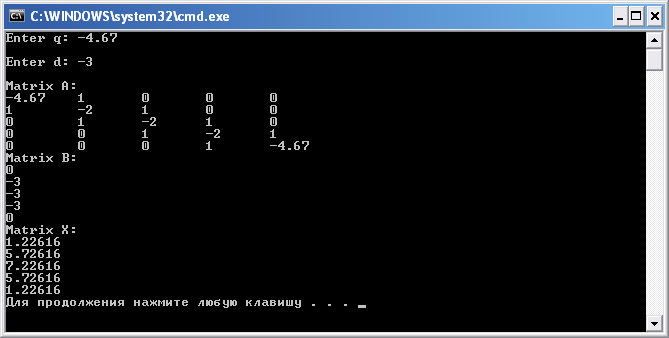
Программа для решения СЛАУ методом прогонки приведена в листинге 1.1.
Результаты работы программы приведены на рис. 1.1.
using namespace std;
2.Аппроксимация функций
Требуется аппроксимировать заданную исходную функцию f(x) многочленом на интервале [a, b]. Задано количество неизвестных параметров n, вид аппроксимации и m — количество точек, в которых задана функция. Таблица исходной функции yi=f(xi) вычисляется в точках xi=a+(i-1)(b-a)/(m-1), i=1, m. Используя полученную таблицу (xi, yi), требуется вычислить значения функций f(xj), φ(xj, c) и погрешность d(xj)=f(xj)-φ(xj, c) в точках xj=a+(j-1)(b-a)/20, j=1, 20.
Общего вида POL
Решение:
Код программы приведен в листинге 2.1.
Результаты работы программы приведены на рис. 2.1.
using namespace std;
double countF(double x)
X[t] = 0; Y[t] = 0; L[t] = 0; D[t] = 0;
X[i] = a + (i — 1)*(b — a)/(m — 1);
for(int j = s-1;j >= 2;j—)

Ограничение
Для продолжения скачивания необходимо пройти капчу:
Источник: studfile.net