Программа реализующая алгоритм шифрования и дешифрования сообщения rsa

Содержание

Автор(ы): Короткова Дарья Алексеевна
Рубрика: Технические науки
Журнал: «Евразийский Научный Журнал №1 2017» (январь, 2017)
Количество просмотров статьи: 6852
Показать PDF версию Схема шифрования RSA и её программная реализация

Информация — это одна из самых ценных вещей в современной жизни. Появление глобальных компьютерных сетей сделало простым получение доступа к информации для людей и для организаций. А так же, доступ к личной информации при её передаче получают злоумышленники.

Чтобы обеспечить безопасность личных данных при передаче, необходимо зашифровывать информацию.

Шифрование — это метод защиты любой информации от неавторизованных лиц, с предоставлением, в это же время, авторизованным пользователям доступа к ней.

В данной статье я рассмотрю метод шифрования RSA и метод дополнительного шифрования OAEP, напишу его программную реализацию и сымитирую атаки на RSA.

RSA— криптографический алгоритм с открытым ключом, разработан учёными Ривестом, Шамиром и Адлеманом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел.

RSA алгоритм. Шифровка. Информационная безопасность, криптография, тайнопись. Простые числа.

Криптографическая система с открытым ключом — система шифрования, при которой открытый ключ передаётся по незащищенному каналу и используется для проверки электронных подписей и для шифрования сообщения. Для генерации электронной подписи и расшифровки сообщений используется закрытый ключ.

Криптографические системы с открытым ключом используют односторонние функции, обладающие свойствами:

· Если известно x, то вычислить f(x) просто.

· Если известно y=f(x), то для вычисления x нет простого пути.

1. Создание открытого и закрытого ключа.

1. Выбирается два простых числа u и v.

2. Вычисляется произведение p=u*v.

3. Вычисляется функция Эйлера φ(p)=(u-1)(v-1)

4. Выбираем открытую экспоненту e (1

5. Вычисляем закрытую экспоненту d, где (d*e) mod φ(p) =1

6. Получаем открытый ключ (e, p) и закрытый ключ (d, p).

2. Шифрование и дешифрование.

Посмотрим модель шифрования и дешифрования сообщения на конкретном примере. Пусть Алиса хочет послать Бобу сообщение h.

У Алисы есть открытый ключ Боба. А Боб владеет своим закрытым ключом.

w=G(h)= h e mod p h=Q(w)=w d mod p

Безопасность схемы шифрования RSA:

Я написала программу на языке высокого уровня С++, где каждый символ кодируется на основании таблицы ASCII, и затем осуществляется алгоритм RSA.

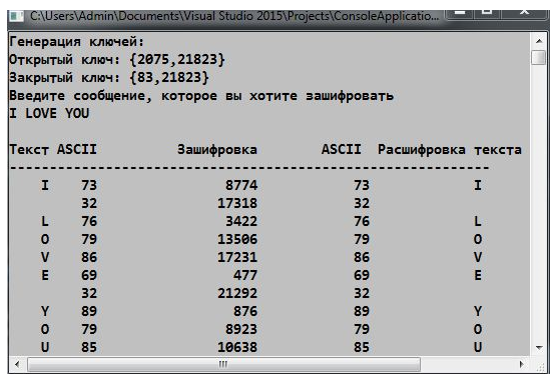
Например, берем символ I, по таблице ASCII его код равен 73. Генерация ключей такая же, как и в примере написанной программы.

w=G(h)= h e mod p = 73 2075 mod 21823=8774; (посчитано на инженерном стандартном калькуляторе в операционной системе Windows)

Основы Шифрования за 5 минут — Asymmetric Cryptography — #ityoutubersru

h=Q(w)=w d mod p = 8774 83 mod 21823 = 73 = I

Надёжность шифрования обеспечивается тем, что третьему лицу (старающемуся взломать шифр) очень трудно вычислить закрытый ключ по открытому. Оба ключа вычисляются из одной пары простых чисел (v и u). То есть ключи связаны между собой. Но установить эту связь очень сложно. Основной загвоздкой является декомпозиция модуля на простые сомножители v и u. Если число является произведением двух очень больших простых чисел, что его очень трудно разложить на множители.

Некоторые атаки на RSA.

1. Разложение на множители.

Реализуется на подборе простых чисел u, v, для надёжности числа должны быть большими.

2. Выборка шифрованного текста.

Пусть Ева перехватывает сообщение w от Алисы к Бобу w=z e (mod n), где z- открытый текст, е — открытый ключ; Ева выбирает число r, r

Ева передает Y бобу для дешифрования и получает g = y d mod n. Ева может легко найти z

g= y d mod n=(w*x e ) d mod n = (w d *x ed )mod n = (w d *x) mod n =(z*x)mod n
z= (z*x) mod n -> z=w*x -1 mod n
3. Исходный текст.

Это показывает, что применение на практике шифрования RSA обладает низкой криптостойкостью, поэтому пользуются схемой дополнительного шифрования OAEP.

Оптимальное асимметричное дополнение шифрования (OAEP — Optimal Assimetric Encryption Padding) — схема дополнения, обычно используемая совместно с какой-либо односторонней функцией с потайным входом (например RSA или функции Рабина) для повышения криптостойкости последней.

Шифрование. Ниже показаны шаги процесса шифрования.

Дополняем сообщение, чтобы сделать его w -битовым. Обозначим его W.
Выбираем случайное число s (одноразовое число) из k бит.
Используем общедоступную одностороннюю функцию G, которая принимает целое s -битовое число, и создает w -разрядное целое число (w — размера W, и s
Применяет маску, G (s), чтобы создать первую часть исходного текста P1=W+G(s) является замаскированным сообщением.
Создаём вторую часть исходного текста P2 = H(P1) + s. Функция H — другая общедоступная функция, которая принимает w -битовые входные сообщения и создает k -битовые выходные сообщения.
Cоздаём C = P e = (P1 || P2) e и передаём C.

Дешифрование. Следующие шаги показывают процесс дешифрования:

Создаём P = C d = (P1 || P2).
Обновляем значение s, используя H(P1) + P2= H(P1) + H(P2) + s =s.
Применяет G(s) + P = G(s) + G(s) + W=W , чтобы обновить значение дополненного сообщения.
После удаления дополнения W, находим первоначальное сообщение.

RSA — Алгоритм шифрования

«Алгоритм шифрования RSA»
Учебная программа на C++ Visual Studio 2012.

С длиной ключа 256 бит;
С длиной ключа 512 бит;

Задание:

Программно реализовать алгоритм шифрования и дешифрования с помощью открытого ключа — алгоритм RSA для любых типов файлов.

Размер генерируемого ключа должен быть 32 (или 64, или 128) байт, или соответственно 256 (или 512, или 1024) бит.

Реализовать создание цифровой подписи с использованием RSA для любых типов файлов, а также проверку на соответствие файла его цифровой подписи.

Решение:

На мой взгляд, первая часть задачи «Генерация ключей» RSA наиболее сложная.
Вторая часть наиболее легкая – это кодирование и декодирование.
Третья часть «Цифровая подпись» занимает промежуточное положение по сложности…
Но для того, чтобы приступить к любой из частей задачи, у Вас должен быть готов программный аппарат для «длинной арифметики». Без этого никуда… При чем целесообразно максимальную длину (32 или 64, или 128 байт) задать константой, чтобы можно было легко перестроить программу на другую длину пакета…

И так, первая часть:

Генерация открытого и закрытого ключей в алгоритме RSA

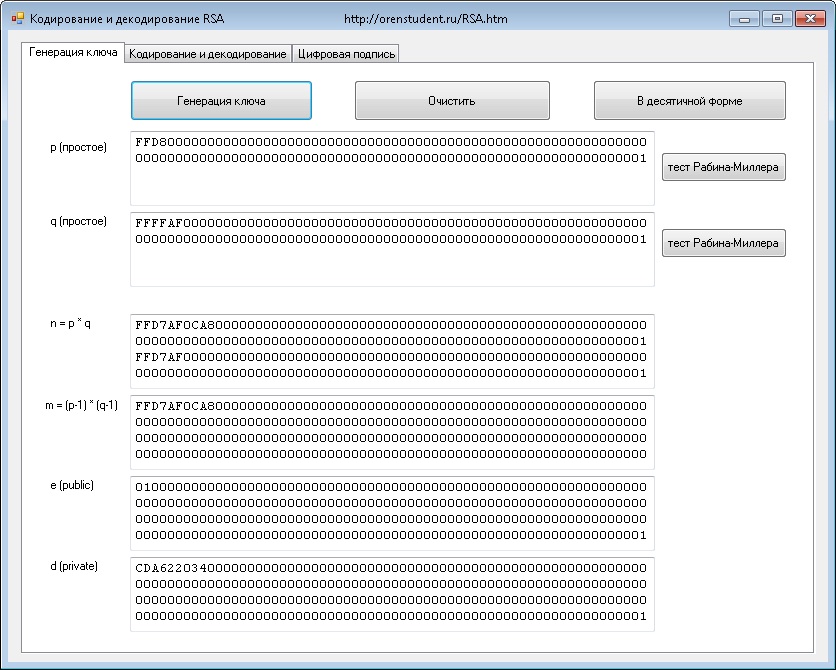
Учебная программа - генерация ключа для алгоритма шифрования RSA

Цель: найти три длинных числа – n, e, d (модуль, открытая и закрытая экспоненты)! Их длины должны быть равны заданной длине пакета.
Прежде всего, находятся длинные простые числа p и q (их длина равна половине длины пакета).
Даже самый легкий и быстрый тест на простоту – «Тест Рабина-Миллера» (одноименные кнопки предназначены для каждого из чисел) заставляет поскучать у компьютера в ожидании результата…

Для скорости последующих вычислений желательно получить длинные числа с большим количеством нулевых битов. Обратите внимание, на картинке p и q представленные в 16-ричной форме, а если 16-ричная цифра равна 0, то все 4 бита этой цифры, также будут равны нулям.

Далее (когда простые числа получены и видны на форме) необходимо щелкнуть кнопку «Генерация ключа» для автоматического заполнения пустых полей…
Это уже легко и быстро: n (для нахождения остатка по модулю) получаем перемножением p и q.
Функцию Эйлера m тоже без труда получаем перемножением p-1 и q-1.
Открытая экспонента е выбирается большего по возможности размера, но с максимальным количеством нулевых битов (для скорости возведения в степень). Если текстовое поле для е пустое, то программа сама подберет значение открытой экспоненты… Но если Вы пожелали ввести в поле для е свое длинное число до щелчка по кнопке «Генерация ключа», то программа его примет по возможности…
А вот закрытую экспоненту d, мультипликативно обратную к числу е по модулю m, вычисляет специальная функция

CLongRsaNum *Get_d(CLongRsaNum *m_op1, CLongRsaNum *e_op2);

Эта функция входит в модуль ArifmeticRSA.cpp , как и сам класс длинных чисел CLongRsaNum.
Видно, что, получая в виде параметров m и e, функция в результате вернет указатель на длинное число d, именно, мультипликативно обратное к числу е по модулю m…

В общем, ничего сложного, если модуль длинной арифметики работает безошибочно. Тестируйте…

Кодирование и декодирование по алгоритму RSA

И так, часть вторая:

Процесс RSA кодирования : файл рубится на пакеты заданной длины и вне зависимости, что находилось в файле (текст, музыка, изображение), каждый пакет рассматривается, как последовательность бит, а значит как длинное число. Внимание! Кодирование производится открытым ключом того респондента, кому предназначено послание.
Zp = Op^e mod n – закрытый пакет, длинное число полученное путем взятия остатка по модулю n от возведения в степень открытой экспоненты е открытого пакета Ор. Понятно, что длины пакетов Op и Zp будут совпадать.
Только человек, обладающий соответствующим закрытым ключом (d и n) сможет расшифровать пакеты послания. Декодирование RSA (обратная операция) Ор=Zp^d mod n
Вот поэтому я и говорил, что вторая часть наиболее простая! И кодирование, и декодирование выполняется одной функцией (кодеком)

Первый параметр – указатель на пакет (открытый или закрытый)
Второй параметр – размер пакета
Третий параметр – экспонента (открытая или закрытая)
Четвертый параметр – модуль для взятия остатка.

Создание цифровой подписи файла, используя алгоритм RSA

И, наконец, третья часть:

Суть цифровой подписи – это гарантия того, что подписанный файл не был изменен с момента создания цифровой подписи автором файла.

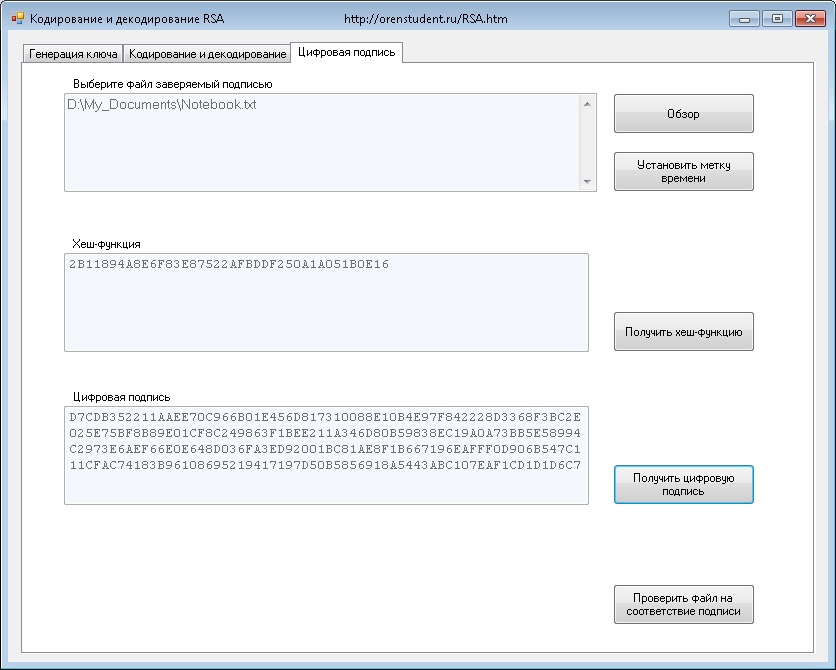
Учебная программа - Создание Цифровой подписи файла алгоритмом шифрования RSA

В жизни это выглядит так:
Автор файла с очень важными данными перед его отправкой щелкает кнопку «Получить цифровую подпись» (что предварительно надо выбрать, т.е. указать сам файл в верхнем окне, Вы догадались? )…

Генерации цифровой подписи

Прежде всего, файл хешируется или, другими словами, вычисляется его хеш-функция!
В данной работе требовалось использовать SHA-1 (Secure Hash Algorithm 1 — алгоритм криптографического хеширования), суть которого прекрасно описана в Рунете. Какого бы большого размера не был исходный файл, результатом работы SHA-1 будет хеш-функция размером 32 байта (160 бит).

Даже если Вы незначительно измените содержимое файла (добавите один пробел в конце или замените одну маленькую букву на заглавную), новая хеш-функция будет очень сильно отличаться от первоначальной. Подобрать специально два разных текста, которые бы имели одинаковые хеш-функции – задача не из легких…

Если полученную хеш-функцию закрыть секретным ключом автора, то и получится цифровая подпись данного файла. Размер ее всегда будет равен размеру пакета, т.к. берется остаток по модулю n.

Еще раз подчеркиваю, что никто кроме автора не может создать цифровую подпись, но все обладатели открытого ключа автора, могут из цифровой подписи получить хеш-функцию подписанного (начального, не искаженного) файла.

Проверка файла на соответствие подписи

Поскольку SHA-1 является общедоступной, то респондент, желающий убедиться в подлинности файла, хеширует его и сравнивает с хеш-функцией полученной путем декодирования из цифровой подписи… Если совпадают, то файл не изменялся и его данным можно доверять…

Можете протестировать:
создав цифровую подпись, нажмите «Проверить файл на соответствие подписи»… получите ответ о соответствии. Затем измените файл (сохранив изменения, пусть самые незначительные) и еще раз нажмите «Проверить файл на соответствие подписи» — ответ уже будет отрицательным.

Обмануть этот механизм, ох как сложно…

Источник: orenstudent.ru

RSA шифрование через библиотеку OpenSSL в Delphi

По долгу службы в разработчиках повстречалась задача шифровать текстовые строки алгоритмом RSA, используя публичный и секретный ключи в PEM формате. При изучении данного вопроса выбор пал на использование библиотеки OpenSSL. Хочу поделиться примерами реализации функциональности шифрования на Delphi. Действия выполнялись в ОС Windows, среда разработки Borland Delphi 7.

С чего начать?

В первую очередь необходим пакет openssl, а точнее библиотека libeay32.dll. И для подключения библиотеки нам понадобится готовый юнит libeay32.pas, который необходимо подключить к проекту. В моем примере отсутствует функциональность генерации ключей из проекта, как это сделать можно будет почитать в материале по ссылке снизу статьи. Для генерации пары ключей я использовал сам openssl следующими командами из cmd:
Генерируем приватный ключ и из него извлекаем публичным ключ

openssl genrsa 1024 > private.pem openssl rsa -in private.pem -pubout > public.pem

Где 1024 является битностью ключа. Отмечу, что от битности ключа зависит и длина строки для шифрования. Если ключ 1024 бита, то зашифровать сможем всего 128 байт, тот самый размер, которому равен размеру ключа. Ниже покажу функцию, определяющие размер структуры RSA ключа.

Но это не все. Данный буфер уменьшится на 11 байт, если во время шифрования указать параметр padding, отвечающего за выравнивания данных — PKCS#1.

Сгенерировав ключ в 2048 бит, сможем зашифровать 256 байт. При этом увеличивается размер выходного шифрованного текста, даже если будет зашифрован всего 1 байт.

Для моей задачи было достаточно 117 байт, в которые умещались карточные данные, размер строк в базе, конечно же, значительно вырос. Но того требует безопасность.

Основные функции

Основное, что мы будем использовать для шифрования, — это:

Инициализация крипто функций

OpenSSL_add_all_algorithms; OpenSSL_add_all_ciphers; OpenSSL_add_all_digests; ERR_load_crypto_strings; ERR_load_RSA_strings;
EVP_cleanup; ERR_free_strings;

Чтение ключей

//чтение секретного ключа в формате PEM, возвращает структуру RSA //Где bp файл ключа, возвращаемый в RSA структуру указывающей x, cb – адрес функции запрашиваемая пароль к ключу. function PEM_read_bio_PrivateKey(bp: pBIO; var x: pEVP_PKEY; cb: TPWCallbackFunction; u: pointer): pEVP_PKEY; cdecl; //чтение публичного ключа в формате PEM, возвращает структуру RSA function PEM_read_bio_PUBKEY(bp: pBIO; var x: pEVP_PKEY; cb: TPWCallbackFunction; u: pointer): pEVP_PKEY; cdecl;

И функции шифрации/дешифрации

//Шифрование/дешифрование flen размера буфера from в буфер _to используя структуру RSA ключа загруженного ранее в режиме выравнивания //данных padding. Получаем длину шифрованного/дешифрованного буфера или -1 при ошибке //Шифрование публичным ключом function RSA_public_encrypt(flen: integer; from: PCharacter; _to: PCharacter; rsa: pRSA; padding: integer): integer; cdecl; //Шифрование секретным ключом function RSA_private_encrypt(flen: integer; from: PCharacter; _to: PCharacter; rsa: pRSA; padding: integer): integer; cdecl; //Дешифрование публичным ключом function RSA_public_decrypt(flen: integer; from: PCharacter; _to: PCharacter; rsa: pRSA; padding: integer): integer; cdecl; //Дешифрование секретным ключом function RSA_private_decrypt(flen: integer; from: PCharacter; _to: PCharacter; rsa: pRSA; padding: integer): integer; cdecl;

Приступим к реализации

Итак, мы имеем сгенерированные ключи, dll-ка лежит в папке с проектом, liblea32.pas подключен в uses. Вызываем процедуры инициализации openssl:

procedure LoadSSL; begin OpenSSL_add_all_algorithms; OpenSSL_add_all_ciphers; OpenSSL_add_all_digests; ERR_load_crypto_strings; ERR_load_RSA_strings; end; procedure FreeSSL; begin EVP_cleanup; ERR_free_strings; end;

Пишем функции загрузки ключей.

KeyFile – пусть до ключа (‘C:key.pem’):

function LoadPublicKey(KeyFile: string) :pEVP_PKEY ; var mem: pBIO; k: pEVP_PKEY; begin k:=nil; mem := BIO_new(BIO_s_file()); //BIO типа файл BIO_read_filename(mem, PAnsiChar(KeyFile)); // чтение файла ключа в BIO try result := PEM_read_bio_PUBKEY(mem, k, nil, nil); //преобразование BIO в структуру pEVP_PKEY, третий параметр указан nil, означает для ключа не нужно запрашивать пароль finally BIO_free_all(mem); end; end; function LoadPrivateKey(KeyFile: string) :pEVP_PKEY; var mem: pBIO; k: pEVP_PKEY; begin k := nil; mem := BIO_new(BIO_s_file()); BIO_read_filename(mem, PAnsiChar(KeyFile)); try result := PEM_read_bio_PrivateKey(mem, k, nil, nil); finally BIO_free_all(mem); end; end;

Вызов функций чтения ключей и обработка ошибок

var FPublicKey: pEVP_PKEY; FPrivateKey: pEVP_PKEY; err: Cardinal; … FPublicKey := LoadPublicKey(‘C:public.key’); FPrivateKey := LoadPrivateKey(‘C:private.key’); //if FPrivateKey = nil then // если ключ не вернулся, то читаем ошибку if FPublicKey = nil then begin err := ERR_get_error; repeat log.Lines.Add(string(ERR_error_string(err, nil))); err := ERR_get_error; until err = 0; end;

Шифрование (Публичным ключом)

var rsa: pRSA; // структура RSA size: Integer; FCryptedBuffer: pointer; // Выходной буфер b64, mem: pBIO; str, data: AnsiString; len, b64len: Integer; penc64: PAnsiChar; size: Integer; err: Cardinal begin rsa := EVP_PKEY_get1_RSA(FPrivateKey); // Получение RSA структуры EVP_PKEY_free(FPrivateKey); // Освобождение pEVP_PKEY size := RSA_size(rsa); // Получение размера ключа GetMem(FCryptedBuffer, size); // Определение размера выходящего буфера str := AnsiString(‘Some text to encrypt’); // Строка для шифрования //Шифрование len := RSA_public_encrypt(Length(str), // Размер строки для шифрования PAnsiChar(str), // Строка шифрования FCryptedBuffer, // Выходной буфер rsa, // Структура ключа RSA_PKCS1_PADDING // Определение выравнивания ); if len > 0 then // длина буфера после шифрования begin // полученный бинарный буфер преобразуем в человекоподобный base64 b64 := BIO_new(BIO_f_base64); // BIO типа base64 mem := BIO_push(b64, BIO_new(BIO_s_mem)); // Stream try BIO_write(mem, FCryptedBuffer, len); // Запись в Stream бинарного выходного буфера BIO_flush(mem); b64len := BIO_get_mem_data(mem, penc64); //получаем размер строки в base64 SetLength(data, b64len); // задаем размер выходному буферу Move(penc64^, PAnsiChar(data)^, b64len); // Перечитываем в буфер data строку в base64 finally BIO_free_all(mem); end; end else begin // читаем ошибку, если длина шифрованной строки -1 err := ERR_get_error; repeat log.Lines.Add(string(ERR_error_string(err, nil))); err := ERR_get_error; until err = 0; end; RSA_free(rsa); end;

Дешифрование (секретным ключом)

var rsa: pRSA; out_: AnsiString; str, data: PAnsiChar; len, b64len: Integer; penc64: PAnsiChar; b64, mem, bio_out, bio: pBIO; size: Integer; err: Cardinal; begin //ACryptedData : string; // Строка в base64 rsa := EVP_PKEY_get1_RSA(FPublicKey); size := RSA_size(rsa); GetMem(data, size); // Определяем размер выходному буферу дешифрованной строки GetMem(str, size); // Определяем размер шифрованному буферу после конвертации из base64 //Decode base64 b64 := BIO_new(BIO_f_base64); mem := BIO_new_mem_buf(PAnsiChar(ACryptedData), Length(ACryptedData)); BIO_flush(mem); mem := BIO_push(b64, mem); BIO_read(mem, str , Length(ACryptedData)); // Получаем шифрованную строку в бинарном виде BIO_free_all(mem); // Дешифрование len := RSA_private_decrypt(size, PAnsiChar(str), data, rsa, RSA_PKCS1_PADDING); if len > 0 then begin // в буфер data данные расшифровываются с «мусором» в конца, очищаем, определяем размер переменной out_ и переписываем в нее нужное количество байт из data SetLength(out_, len); Move(data^, PAnsiChar(out_ )^, len); end else begin // читаем ошибку, если длина шифрованной строки -1 err := ERR_get_error; repeat log.Lines.Add(string(ERR_error_string(err, nil))); err := ERR_get_error; until err = 0; end; end;

И заключении пример чтения ключа «зашитого» в приложение

В примере указан приватный ключ и его чтение, с таким же успехом «зашивается» и читается публичный ключ функцией PEM_read_bio_PUBKEY

var mem, keybio: pBIO; k: pEVP_PKEY; keystring: AnsiString; begin keystring := ‘——BEGIN RSA PRIVATE KEY——‘ + #10 + ‘MIICXgIBAAKBgQCfydli2u2kJfb2WetkOekjzQIg7bIuU7AzAlBUPuA72UYXWnQ/’ + #10 + ‘XcdSzEEMWSBLP7FO1vyVXR4Eb0/WqthF0ZViOK5bCN9CnR/1GMMiSqmIdByv/gUe’ + #10 + ‘Z/UjGrKmxeQOoa2Yt0MJC64cNXgnKmYC7ui3A12LlvNdBBEF3WpcDbv+PQIDAQAB’ + #10 + ‘AoGBAJnxukKHchSHjxthHmv9byRSyw42c0g20LcUL5g6y4Zdmi29s+moy/R1XOYs’ + #10 + ‘p/RXdNfkQI0WnWjgZScIij0Z4rSs39uh7eQ5qxK+NH3QIWeR2ZNIno9jAXPn2bkQ’ + #10 + ‘odS8FPzbZM9wHhpRvKW4FNPXqTc3ZkTcxi4zOwOdlECf9G+BAkEAzsJHgW1Isyac’ + #10 + ‘I61MDu2qjMUwOdOBYS8GwEBfi/vbn/duwZIBXG/BZ7Pn+cBwImfksEXwx0MTkgF3’ + #10 + ‘gyaChUSu+QJBAMXX3d94TwcF7lG9zkzc+AR/Onl4Z5UAb1GmUV57oYIFVgW1RIOk’ + #10 + ‘vqynXWrTjTOg9C9j+VEpBG67LcnkwU16JmUCQH7pukKz9kAhnw43PcycDmhCUgvs’ + #10 + ‘zCn/V8GCwiOHAZT7qLyhBrzazHj/cZFYknxMEZAyHk3x2n1w8Q9MACoVsuECQQDF’ + #10 + ‘U7cyara31IyM7vlS5JpjMdrKyPLXRKXDFFXYHQtLubLA4rlBbBHZ9txP7kzJj+G9’ + #10 + ‘WsOS1YxcPUlAM28xrYGZAkEArVKJHX4dF8UUtfvyv78muXJZNXTwmaaFy02xjtR5’ + #10 + ‘uXWT1QjVN2a6jv6AW7ukXiSoE/spgfvdoriMk2JSs88nUw==’ + #10 + ‘——END RSA PRIVATE KEY——‘ ; k := nil; keybio := BIO_new_mem_buf(Pchar(keystring), -1); mem := BIO_new(BIO_s_mem()); BIO_read(mem, PAnsiChar(keystring), length(PAnsiChar(keystring))); try result := PEM_read_bio_PrivateKey(keybio, k, nil, nil); finally BIO_free_all(mem); end; end;

На этом мои примеры реализации заканчиваются. Исходники проекта доступны на Github.

Иточники:

Статья Владимира Мешкова «Используем средства библиотеки OpenSSL для криптографической защиты данных»
Пример шифрования файла
Пример чтения ключа с запросом пароля от автора libeay32.pas
Создание пары ключей, проверка отпечатка SHA1 и кое что еще

UPD
Из дискуссий в комментариях внесу дополнения: если мы зашифровываем нужную нам строку публичным ключом, то расшифровывается она только секретным и наоборот — если секретным, то расшифровать можно только публичным ключом. В моем случае у клиента публичный ключ, которым он шифрует данные и только на сервере их можно расшифровать секретным ключом.

Источник: habr.com

RSA — Алгоритм шифрования

«Алгоритм шифрования RSA» Учебная программа на C++ Visual Studio 2012.

С длиной ключа 256 бит; С длиной ключа 512 бит;