Наибольший общий делитель (НОД) чисел 3430 и 1365 – это 35. Другими словами, 35 – наибольшее число, на которое и 3430 и 1365 делятся без остатка. Чтобы убедиться в этом, разложим оба числа на простые сомножители:
3430 = 2 * 5 * 7 * 7 * 7 1365 = 3 * 5 * 7 * 13
и выделим пары общих сомножителей. В данном случае это пары 5 и 7. Наибольший общий делитель – это произведение совпадающих сомножителей; в данном случае это 5 * 7 = 35.
Более изящный метод поиска НОД – алгоритм Евклида. Найдем остаток от деления 3430 на 1365:
3430 mod 1365 = 700
Так как этот остаток не равен нулю, повторим то же действие, подставив вместо первого числа второе, а вместо второго – остаток:
1365 mod 700 = 665
Этот остаток также не нуль, поэтому еще одно деление:
700 mod 665 = 35
665 mod 35 = 0
Теперь остаток – нуль, следовательно, НОД равен 35. Вот и отлично.
Следующая программа на Паскале использует метод Эвклида и рекурсию:
var a, b, c, answer: integer; function gcd(m, n: integer): integer; var modulo: integer; begin modulo := m mod n; if modulo = 0 then gcd := n else gcd := gcd (n, modulo) end; begin write(‘Enter two numbers: ‘); readln(a, b); if a < b then begin c := a; a := b; b := c; end; answer := gcd(a, b); writeln(‘Greatest common divisor: ‘, answer); end.
Если представить, что в функцию сразу подставляются числа 665 и 35, то сразу ясно, как вычисляется gcd(665, 35) : остаток modulo будет равен нулю и функция возвратит число 35 (ветка if ). А вот при обращении gcd(3430, 1365) modulo будет равен 700, и, следовательно, функция вызовет себя еще раз в виде gcd(1365, 700) . Таким образом, при каждом обращении Паскаль как бы создает новую копию функции gcd :
Алгоритм Евклида. Классический с вычитанием и быстрый с «делением»
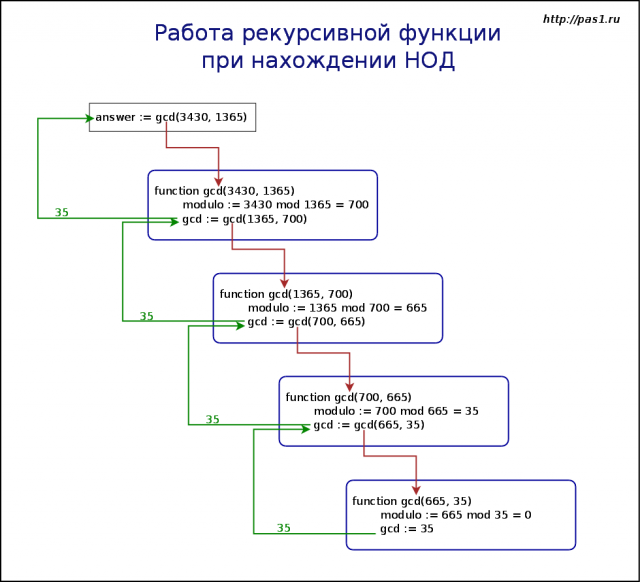
- Из основной ветки программы вызывается функция gcd . Результат работы данной функции в дальнейшем будет присвоен переменной answer .
- В функции gcd вычисляется остаток от деления чисел 3430 и 1365. Поскольку он не равен нулю, то осуществляется повторный вызов функции, но уже с числами 1365 и 700 (700 – это остаток от первого деления).
- При третьем вызове функции передаются числа 700 и 665.
- При четвертом – 665 и 35. Здесь остаток равен 0. Следовательно, результатом работы функции является число 35 ( gcd = 35 ).
- Результат четвертого вызова возвращается в третий.
- Третий – во второй.
- Второй – в первый.
- Первый – в основную ветку программы и присваивается переменной answer .
Источник: pas1.ru
Алгоритм Евклида для вычисления НОД — Pascal ABC
Алгоритм Евклида для вычисления наибольшего общего делителя двух натуральных чисел, формулируется так: нужно заменять большее число на разность большего и меньшего до тех пор, пока одно из них не станет равно нулю; тогда второе и есть НОД. Напишите программу, которая реализует этот алгоритм. Входные данные Входная строка содержит два числа, разделённые пробелом – a и b . Выходные данные Программа должна вывести в одной строке два числа: сначала наибольший общий делитель двух введённых чисел, а затем – количество шагов цикла, которые были выполнены.
Алгоритм Евклида
Код к задаче: «Алгоритм Евклида для вычисления НОД»
Листинг программы
var a, b, nod, k: integer; begin readln(a, b); k := 0; while (a <> 0) and (b <> 0) do begin if a > b then a := a mod b else b := b mod a; k := k + 1; end; nod := a + b; writeln(nod, ‘ ‘, k); end.
Источник: studassistent.ru
Программа реализующая алгоритм евклида на паскале

Алгоритм Евклида. НОД
Здравствуйте, дорогие читатели! Как и было обещано в прошлой статье, сегодня я пишу о НОД. Естественно, у многих сразу появился вопрос, что это такое. Объясняю. НОД расшифровывается как Наибольший Общий Делитель. То есть разговор ведется о наибольшем делителе для двух чисел одновременно.
Приведу пример: имеется два числа — 24 и 9. Самое большое число, на которое они оба делятся без остатка — это число 3, которое и будет являться НОД. Также, когда говорят об наибольшем общем делителе, упоминают о загадочном для некоторых алгоритме Евклида. На самом деле все гораздо проще. Дело в том, что алгоритм Евклида — это такой алгоритм, который как раз таки и позволяет найти НОД.
Но следует запомнить, что алгоритм рассчитан на действия с двумя целыми неотрицательными числами. Это важный момент, который нельзя упускать.
Теперь посмотрим на принцип алгоритма, в котором используется деление с остатком.
Расписываю по пунктам алгоритм Евклида:
- Берем два целых неотрицательных числа
2. Сравниваем их и находим остаток от деления большего числа на меньшее.
3. Если остаток равен 0, то это значит, что делитель и есть НОД (Выходим из цикла).
4. Если же в результате деления мы получили не 0 в остатке, то большему числу присваиваем остаток, который получили в пункте 2 (заменяем большее число на остаток от деления).
5. Возвращаемся к пункту 2.
Для тех, кому все еще не понятно, приведу блок-схему алгоритма на примере двух чисел, пусть это будут числа a и b.
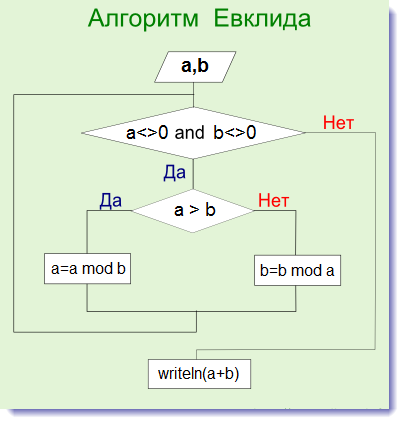
Вернемся к нашему примеру с числами 24 и 9. Опишу пошагово, как, используя алгоритм Евклида, мы приходим к тому, что НОД в этом случае равно 3
- Берем числа m = 24 и n = 9.
- m > n
3. m := m mod n
4. m > n
7. m := m mod n
8. т.к m = 0 выходим из цикла. НОД равен n = 3
Ну а сейчас алгоритм Евклида в паскале.
Источник: programmado.ru