Онлайн-калькулятор вычисляет расстояние между двумя точками по географическим координатам в считанные секунды, используя специальные формулы. Задайте только исходные данные для расчетов, и после нажатия кнопки «Рассчитать» вы узнаете точный ответ.
Широта первой точки
Долгота первой точки
Широта второй точки
Долгота второй точки
Точность вычисления
Знаков после запятой: 3
Рассчитать
Расстояние
Расстояние между двумя географическими координатами при помощи обычной карты определить достаточно сложно. В данном случае не учитывается кривизна сферы, поскольку наша планета условно имеет форму шара. Проблема усугубляется неровностью рельефа, где могут преобладать горы, равнинная местность, овраги. Все это также накладывает свой отпечаток на выведение корректных результатов.
Как пользоваться калькулятором
- введите в пустые строки значения широты и долготы для первой точки;
- укажите в строках широты и долготы координаты на местности для второй точки.
После нажатия на кнопку «Рассчитать» в окне появится результат.
Географическая широта и географическая долгота. Географические координаты. Видеоурок по географии
Например, зная точное положение Москвы (55,7522 гр. с.ш., 37.6156 гр. в.д.) и Санкт-Петербурга (59,89444 град. с.ш., 30,26417 град. в.д.) на карте, мы можем узнать, на каком расстоянии они находятся друг от друга. Используя эти числа, получим 633 км.
Источник: calck.ru
Расстояние между двумя координатами
Широту и долготу двух точек, между которыми необходимо найти расстояние, следует указывать в градусах в виде десятичной дроби. Например, расстояние между Москвой (55.75059; 37.61777) и Киевом (50.44952; 30.52537) составляет 755 километров.
Южная широта и западная долгота задаются отрицательной величиной от 0° до -90° и от 0° до -180° соответственно.
Преобразовать координаты из формата «градусы, минуты, секунды» в десятичные градусы можно с помощью конвертера географических координат.
Поделиться страницей в социальных сетях:
Онлайн калькуляторы
Calculatorium.ru — это бесплатные онлайн калькуляторы для самых разнообразных целей: математические калькуляторы, калькуляторы даты и времени, здоровья, финансов. Инструменты для работы с текстом. Конвертеры. Удобное решение различных задач — в учебе, работе, быту.
Актуальная информация
Помимо онлайн калькуляторов, сайт также предоставляет актуальную информацию по курсам валют и криптовалют, заторах на дорогах, праздниках и значимых событиях, случившихся в этот день. Информация из официальных источников, постоянное обновление.
Навигация
Источник: calculatorium.ru
Вычисляем ближайшие объекты по координатам
Я разрабатывал один проект по недвижимости и появилась задача показывать объекты расположенные в радиусе 20 км с просматриваемым. Т.е. у нас есть объект, в нашем случае это поселок, и нужно отображать находящиеся рядом поселки из нашей базы данных в радиусе 20 км, при этом имея только координаты их расположения.
Считаем расстояние по GPS координатам
Исследование
Итак для решения задачи началось «гугление». И первое что было нагуглено это алгоритм расчета расстояний между двумя точками на шаре, статья уходила в Wikipedia. Статья конечно интересное, но как она поможет в моем деле!? Как выяснилось от нее будет толк, но не сразу.
Смысл в том, что просчет расстояний по координатам хорош, но как делать выборку из базы и рассчитывать координаты «на ходу»!? Вероятно данным способом никак. Конечно, решение в лоб было каким то образом просчитать насколько можно сдвинуться от координаты чтобы получить нужное расстояние и запросить через какой-нибудь SQL BETWEEN.
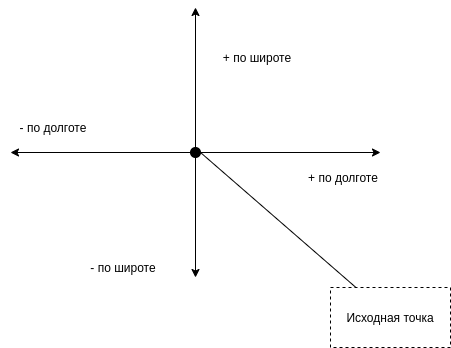
Взять изначальную точку координат, и прибавить к ней число градусов соответствующее расстоянию, необходимому для выборки.
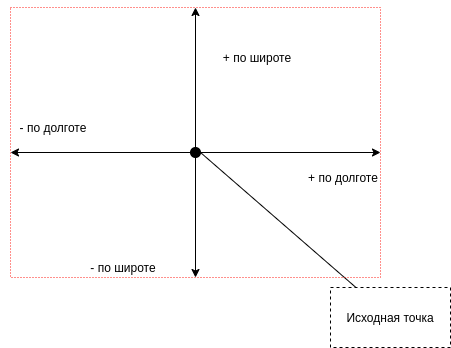
Если соединить эти точки, на которые мы прибавили изначальную координату получится квадрат (простите не ровно нарисовал).
Далее с помощью все той же википедии я открыл для себя несколько формул, и одна из них прямо то что нужно. Это формула вычисления длины градуса. Помните в начале я говорил, что 111 км. это слишком абстрактно из первого решения в вопросе. Так вот, эта формула позволяет вычислять длину градуса непосредственно на конкретной меридиане или параллели, нужно только знать радиус нашего шара. Там же на странице википедии есть предварительно рассчитанные данные, по которым можно будет проверить свою формулу
Расчеты
Приступаем к расчетам. Из открытых источников нам известно, что:
- Средний радиус Земли R = 6371210 м.
- Экваториальный радиус Земли RЭ = 6378,245 м.
- Полярный радиус Земли RП = 6356,830 м.
Я для расчетов взял средний радиус. Естественно нужно помнить, что земля все-таки не идеальная сфера, поэтому погрешность есть и в этих расчетах, но для нашей задачи это допустимая погрешность.
Я написал небольшой код для проверки вычислений, и для того, чтобы я мог взять числа и проверить их на реальных данных.
Код для проверки
const EART_RADIUS = 6371210; //Радиус земли const DISTANCE = 20000; //Интересующее нас расстояние //https://en.wikipedia.org/wiki/Longitude#Length_of_a_degree_of_longitude function computeDelta(degrees) < return Math.PI / 180 * EART_RADIUS * Math.cos(deg2rad(degrees)); >function deg2rad(degrees) < return degrees * Math.PI / 180; >const latitude = 55.460531; //Интересующие нас координаты широты const longitude = 37.210488; //Интересующие нас координаты долготы const deltaLat = computeDelta(latitude); //Получаем дельту по широте const deltaLon = computeDelta(longitude); // Дельту по долготе const aroundLat = DISTANCE / deltaLat; // Вычисляем диапазон координат по широте const aroundLon = DISTANCE / deltaLon; // Вычисляем диапазон координат по долготе console.log(aroundLat, aroundLon);
В коде я сразу установил константу расстояния, радиуса земли и принял решение все считать в метрах, поскольку данные я нашел в метрах и лень было разделить их на 1000, да и в метрах казалось, что точность немного выше, чем в километрах с округлением.
Суть этого кода в следующем. Мы не забываем перевести градусы координат в радианы, поскольку формула из википедии рассчитана на радианы. Мы вычисляем дельту ширины и долготы одинаково по одной и той же формуле, поскольку мы условились что у нас идеальный шар и эта погрешность нам допустима. С помощью формулы мы узнаем сколько градусов у нас в одном километре, а дальше простая пропорция.
1 градус — 63046.689652997775 метров
X градусов — 200000 метров
Если 1 градус, соответствует 63046.689652997775 метров (для широты вычисленной из координаты), то 20000 метров соответсвует X. Дальше, как в школе учили, наискосок умножаем на оставшееся делим. И так как там у нас получается умножение на 1, то это действие можно упустить и записать как `DISTANCE / deltaLat`. Тоже самое проделываем для координаты долготы.
На этих конкретных координатах получаются числа 0.31722522007226484 и 0.22583381380662185. По сути это и есть числа, готовые прибавляться к координатам, чтобы получить тот самый заветный квадрат.
Теперь мы можем добавить эти числа в SQL запрос, чтобы посмотреть, что за выборка у нас получится:
select name, latitude, longitude from villages where latitude between 55.460531 — 0.31722522007226484 and 55.460531 + 0.31722522007226484 and longitude between 37.210488 — 0.22583381380662185 and 37.210488 + 0.22583381380662185;

Ну и в моей выборке оказалось 7 объектов. Конечно я взял эту выборку и проверил координаты с помощью линейки на Яндекс Картах. В моем случае все попали в радиус обозначенных 20км. Но мы же помним, что взяли квадрат, а не окружность для вычисления?! Я там даже схему нарисовал в начале, что за квадрат.
Итак, если сделать окружность, внутри этого квадрата, она как раз будет радиусом примерно те же 20 км.

Я добавил картинку для наглядности. Видно, что если высота квадрата 40 км, и в нем окружность, то радиус ее тоже будет соответствовать 20 км. Остаются лишние области — углы квадрата, которые я закрасил зеленым. Это то что у нас может попасть в выборку, но они уже не соответствуют именно радиусу в 20 км. Т.е. это лишние данные.
И вот тут приходит на помощь та самая формула, о которой я говорил в начале — Расчет расстояния между координатами. С помощью этой формулы можно сравнить исходную точку с координатами из выборки и отсечь те, что будут превышать те самые 20 км, поставленные в задаче.
Итог
Задача решена. Алгоритм придуман. Осталось упаковать это в «красивый» и «чистый» код, чтобы все было по феншую. Надеюсь статья была полезной, потому что когда я искал решения задачи, я наткнулся на множество формул, на множество идей, но не нашел места, где это было бы собрано вот так, как попытался собрать я в рамках данной статьи.
Ссылки
1. Изменил картинку с ошибочным радиусом и описание высоты квадрата
Источник: habr.com