Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.
Источник: geleot.ru
Найдите стороны треугольника
Расчет треугольника для Windows
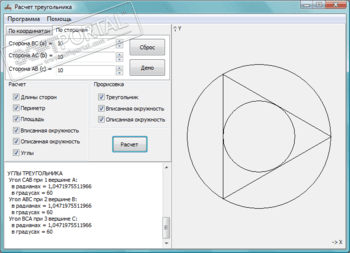
Расчет треугольника — обучающая программа, которая позволяет определить площадь, периметр, углы треугольника, а также рассчитать параметры вписанной и описанной окружности. Треугольник задается координатами своих вершин или длинами своих сторон. Может использоваться для решения геометрических задач при выполнении школьных и студенческих домашних заданий, служить демонстрационным материалом на уроках геометрии, а также исполнять роль калькулятора при выполнении простых геометрических расчетов.
- Изменен алгоритм демо выбора параметров задания треугольника
- Добавлен способ задания треугольника двумя сторонами и углом
ТОП-сегодня раздела «Математика»
MathType — отличное приложение для работы с формулами, математическими выражениями и.
Advanced Grapher — Мощная и простая в использовании программа для построения графиков и их анализа.
Satellite Antenna Alignment — Программа предназначена для расчета углов, необходимых при установке.
SMath Studio — бесплатная программа для вычисления математических выражений и построения.
Отличник — тренажер решения заданий по математике и русскому языку для учащихся 1-4.
GeoGebra — графический калькулятор для функций, геометрии и статистики. Здесь объединены.
Отзывы о программе Расчет треугольника
Отзывов о программе Расчет треугольника 1.5 пока нет, можете добавить.
Источник: www.softportal.com
Сторона треугольника 14 формул расчет онлайн
После проведения расчета нажмите на кнопочку «Расчет не верен» если Вы обнаружили ошибку. Или нажмите «расчет верный» если ошибок нет.
По силам каждому ★ Найдите стороны треугольника на рисунке
Сначала выполните расчет на этом калькуляторе. Затем снова зайдите сюда.
Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.
Как найти длину стороны треугольника?
Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
Для прямоугольного треугольника:
1) Найти катет через гипотенузу и другой катет


где a и b — катеты, с — гипотенуза.
2) Найти гипотенузу по двум катетам


где a и b — катеты, с — гипотенуза.
3) Найти катет по гипотенузе и противолежащему углу


где a и b — катеты, с — гипотенуза,α° и β° — углы напротив катетов.
4) Найти гипотенузу через катет и противолежащий угол


где a и b — катеты, с — гипотенуза,α° и β°- углы напротив катетов.
Для равнобедренного треугольника:
1) Найти основание через боковые стороны и угол между ними


где a — искомое основание, b — известная боковая сторона,α° — угол между боковыми сторонами.
2) Найти основание через боковые стороны и угол при основании


где a — искомое основание,b — известная боковая сторона,β° — угол при осноавнии.
3) Найти боковые стороны по углу между ними


где b — искомая боковая сторона, a — основание,α° — угол между боковыми сторонами.
4) Найти боковые стороны по углу при основании


где b — искомая боковая сторона, a — основание,β° — угол при осноавнии.
Для равностороннего треугольника:
1) Найти сторону через площадь


где a — искомая сторона, S — площадь треугольника.
2) Найти сторону через высоту


где a — искомая сторона,h — высота треугольника.
3) Найти сторону через радиус вписанной окружности


где a — искомая сторона,r — радиус вписанной окружности.
4) Найти сторону через радиус описанной окружности


где a — искомая сторона,R — радиус описанной окружности.
Для произвольного треугольника:
1) Найти сторону через две известные стороны и один угол (теорема косинусов)


где a — искомая сторона, b и с — известные стороны, α° — угол напротив неизвестной стороны.
2) Найти сторону через одну известную сторону и два угла (теорема синусов)


где a — искомая сторона, b — известная сторона, α° и β° известные углы.
Материал слишком сложен? Прочтите связанные статьи:
Источник: mathweb.ru