Платформа выдаст результат в виде сводной таблицы, а также напротив строк модуля будет указано, сколько раз выполнялась данная строка, и каков процент времени ее исполнения в общем времени замера:
Вопрос 05.54 экзамена 1С:Профессионал по платформе. Для начала процесса замера производительности.
- запустить систему в режиме отладки, далее выставить точку останова, запустить замер производительности (Отладка — Замер производительности)
- запустить систему в режиме отладки, запустить замер производительности (Отладка — Замер производительности)
- запустить систему в режиме «Конфигуратор», запустить замер производительности (Отладка — Замер производительности)
- запустить систему в режиме «Конфигуратор», запустить замер производительности (Отладка — Замер производительности), запустить систему в режиме отладки или подключиться к системе для отладки
- все ответы правильные
- можно 1, или 2, или 4
Правильный ответ шестой.
Оценка эффективности выполнения программного кода. Оптимизация вычислений
Вопрос 05.55 экзамена 1С:Профессионал по платформе. В процедуре есть строка кода, которая вызывает функцию. Можно ли произвести замер производительности для данной процедуры, включив в него время выполнения самой строки, но не включив время исполнения функции, вызываемой в строке?
- Нет, время исполнения вызываемой функции всегда будет входить в замер производительности
- Это делается по умолчанию, поскольку в замер производительности всегда входит время исполнения строк самой процедуры, без учета времени вызываемых из нее процедур и функций
- Можно включить или выключить время выполнения вызываемых процедур и функций перед началом замера производительности
- Можно включить или выключить время выполнения вызываемых процедур и функций уже в отчете замера производительности
Правильный ответ четвертый, для этого в отчете предназначена галка Для вызова процедур и функций включать время выполнения:
Вопрос 05.56 экзамена 1С:Профессионал по платформе. Информация в колонке левее текста модуля отображает.
- количество вызовов строки кода в замере производительности и время ее исполнения
- количество вызовов строки кода в замере производительности и процент времени ее исполнения к общему времени замера
- порядковый номер замера производительности и время исполнения строки кода
- порядковый номер замера производительности и процент времени исполнения строки кода по отношению к общему времени замера
Правильный ответ второй.
1 комментарий:

вопрос 5.56 изменился:
5.56 Замер производительности можно выполнить
1. для определенного участка кода (расположенного между точками останова)
2. для кода выполняемого при старте системы (без использования точек останова)
Решения задач, вызвавших затруднения, на основе оценочных процедур по информатике
3. для кода выполняемого при окончании работы системы (без использования точек
останова)
4. Варианты 1 и 2
5. Варианты 1 и 3
6. Верны все варианты
правильный ответ — вариант 6, проверено в официальном тренажере 1с.
примечательно, что картинку забыли убрать — мне кажется, она не имеет отношения к самому вопросу. Ответить Удалить
Источник: about1cerp.blogspot.com
Профилирование программ
Профилирование позволяет оценить время, затрачиваемое на выполнение отдельных операций в программе. Профилирование можно выполнять как для всего кода, так и для его фрагментов.

Для начала рассмотрим профилирование фрагментов кода.
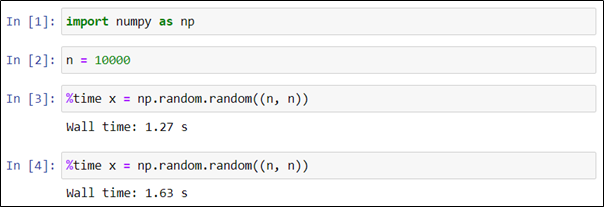
В случае работы в Jupyter notebook можно использовать так называемые “магические команды”. Для того, чтобы узнать время выполнения одной строки, нужно в её начале разместить магическую команду %time. В приведенном ниже примере в последней ячейке тетрадки создается матрица размером 10000×10000, заполненная случайными вещественными числами

Как видно, на это потребовалось 1,27 секунды. Отметим, что повторный запуск аналогичной команды потребовал уже 1,63 секунды.
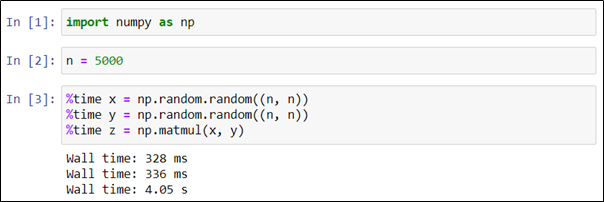
Чтобы оценить время выполнения кода в каждой из строк какой-либо ячейки, необходимо использовать магическую команду %time в каждой строке. В приведенном ниже примере создаются и перемножаются две матрицы размером 5000×5000, заполненные случайными вещественными числами.
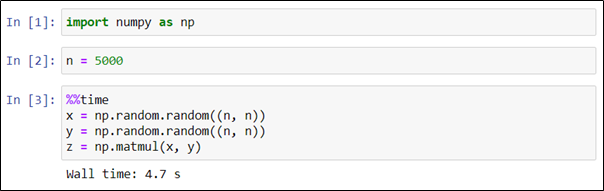
Если же нужно оценить время выполнения ячейки в целом, необходимо использовать команду %%time. Генерация двух матриц и их перемножение потребовали в сумме 4,7 секунды.
Описанные приемы позволяют получить лишь начальное представление о быстродействии кода. Как известно, единичного эксперимента недостаточно для того, чтобы составить адекватное представление о поведении исследуемой системы. Проведем серию экспериментов и возьмем среднее значение в качестве оценки времени выполнения кода. Для этого будем использовать команду %%timeit с ключом -r, задающим количество вычислительных экспериментов.
В следующем примере мы так же генерируем и перемножаем две матрицы в серии из пяти экспериментов.
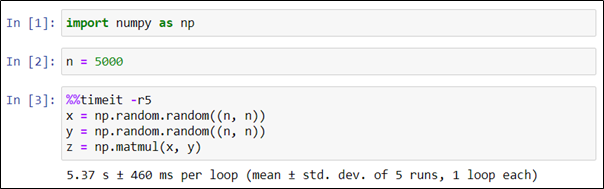
Как видно, среднее значение времени в серии экспериментов (5,37 секунды) отличается от времени единичного эксперимента, проведенного ранее (4,7 секунды).
Рассмотрим еще один пример профилирования кода.
В некоторых случаях имеет смысл сравнить несколько возможных вариантов реализации кода, чтобы выбрать из них наиболее производительный.
Известно, что значение функции “синус” для значений аргумента, близких к нулю, можно представить в виде суммы ряда Маклорена, а приближенное значение вычислить как сумму его первых двух слагаемых.

Исследуем два способа вычисления приближенного значения синуса, отличающихся способом вычисления второго слагаемого: в одном случае через трехкратное перемножение аргумента, в другом — через операцию возведения в степень. Для измерения времени снова воспользуемся командой timeit.
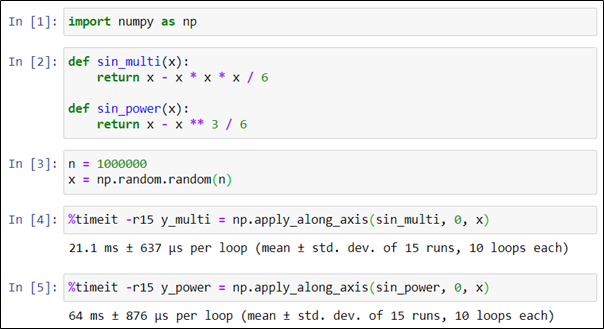
Несмотря на то, что математически эти варианты полностью эквивалентны, вариант с расчетом через перемножение аргументов приблизительно в три раза быстрее варианта с возведением в степень. Этот результат был бы совершенно не очевиден без профилирования.
Перейдем к профилированию кода программы в целом.
Представим, что есть программа min_distance_naive.py, вычисляющая наименьшее расстояние между точками на плоскости и началом координат. Координаты точек представлены матрицей размерности 1000000×2, записанной в файле points.npy. Ключевой фрагмент кода — функция min_dist_naive.
import numpy as np def min_dist_naive(points, base): r_min = float(‘inf’) for p in points: r = ((p[0] — base[0]) ** 2 + (p[1] — base[1]) ** 2) ** (1 / 2) r_min = min(r, r_min) return r_min points = np.load(‘points.npy’) origin = (0, 0) min_dist = min_dist_naive(points, origin) print(min_dist)
Для запуска этой программы необходимо в командной строке выполнить следующую команду:
python min_distance_naive.py
Для запуска профилирования дополним эту команду ключом -m cProfile указывающим, что для профилирования нужно использовать модуль cPython, и ключом -s time, указывающим, что результаты профилирования нужно упорядочить по времени.
python -m cPython -s time min_distance_naive.py > naive.txt
Весь вывод, в том числе результаты профилирования, будут записаны в текстовый файл naive.txt. Анализ этого файла показывает, что время выполнения программы составило 4,369 с., суммарное время выполнения функции поиска минимального расстояния составило 4,132 с.

Теперь попробуем ускорить выполнение кода. Поскольку алгоритм решения задачи построен вокруг сравнения между собой большого количества расстояний, то, принимая во внимание монотонность функции извлечения квадратного корня, можно исключить эту функцию и сравнивать между собой квадраты расстояний. В соответствии с этой идеей несколько доработаем исходную функцию, исключив из цикла операцию извлечения квадратного корня.
import numpy as np def min_dist_optim(points, base): r_min = float(‘inf’) for p in points: r = (p[0] — base[0]) ** 2 + (p[1] — base[1]) ** 2 r_min = min(r, r_min) r_min = r_min ** (1 / 2) return r_min points = np.load(‘points.npy’) origin = (0, 0) min_dist = min_dist_optim(points, origin) print(min_dist)
Запустим профилирование доработанной программы.
python -m cPython -s time min_distance_optimized.py > optimized.txt
Обратимся к результатам профилирования.

В этом случае время выполнения функции составило 3,772 с.
По результатам многократного профилирования обоих вариантов и статистической обработки полученных экспериментальных данных, включающей в том числе сравнение выборок с помощью t-критерия Уэлча, получен статистически значимый результат, свидетельствующий о том, что модифицированная функция приблизительно на 8% быстрее исходной. Таким образом, профилирование помогает выявить узкие места в коде с точки зрения производительности, сравнить разные варианты реализации алгоритмов, и в конечном счете ускорить выполнение программ. Код приведенных примеров, а также экспериментальные данные можно найти в репозитории.
- профилирование
- программ
- Python
- Программирование
- Машинное обучение
Источник: habr.com
Оценка времени выполнения программы. 0
Longobard написал 28 февраля 2004 года в 21:10 (2542 просмотра) Ведет себя как мужчина; открыл 291 тему в форуме, оставил 2499 комментариев на сайте.
Иногда возникает необходимость особенно на олимпиадах оценить время работы алгоритма. По типу » время выполнения этого алгоритма порядка O(N^2*logN) » Как эту величину находить?
decvar 21:15, 28 февраля 2004
это «о» малое от того, что в скобках? Это к Теодору….
Longobard 21:22, 28 февраля 2004
ну запись просто такая. Можно так что » время выполнения этого алгоритма порядка N^2*logN »
anonymous 21:52, 28 февраля 2004
decvar
это «о» малое от того, что в скобках? Это к Теодору….
Нет, это «О большое», то бишь, константа умноженная на то, что в скобках. О малое для программирования — не слишком удобная конструкция.
Оценка же быстодействия алгоритмов — вещь грубая, и точные методы используются только для определения класса задачи — P, NP, и т.д.
Для получения же числа как O(N^2*logN), применяют «палечные» методы. Типа, чтобы убедиться, что в неупорядоченной матрице NxN нет элемента с заданными свойствами, надо перебрать их все. Стало быть, сложность «тупого» алгоритма перебора будет O(N^2).
Посмотри еще здесь:
anonymous 21:54, 28 февраля 2004
Longobard 22:40, 28 февраля 2004
Longobard 22:44, 28 февраля 2004
То есть насколько я понял никаких формул для расчета этого дела нету, просто надо знать что для алгоритмов одного типа значение одно, а для других — другое. Я правильно понял?
anonymous 23:12, 28 февраля 2004
Ну, насколько я (математик, специалист по теории представлений и матфизике) понимаю — да. С другой стороны, «палечные» методы тоже могут быть достаточно точными. Пример.
Ищем число 5 в упорядоченном списке длины N.
Алгоритм 1: Тупо перебираем все элементы «он.не он». Если 5 окажется в самом конце списка, мы сделали N операций. Значит, быстрота алгоритма O(N).
Алгоритм 2: Действуем по принципу «лев в пустыне» — список-то упорядоченный! — делим пустыню пополам, в одной половине лев есть, в другой — нет. Делим список пополам, смотрим на конечные значения. Если 5 между ними — это наш новый список. За K шагов алгоритма список стал в 2^K раз короче, значит, когда 2^K = N, у нас только 1 элемент, и дело сделано за K = logN шагов. Быстрота алгоритма = O(logN).
А с формулами туго, что ты в них подставишь?
Интересно, а есть на форуме профессиональные программисты. Занятно было бы услышать профессиональную оценку моего бреда… 🙂
Longobard 23:35, 28 февраля 2004
Имхо это не бред.
decvar 20:49, 29 февраля 2004
Ну, насколько я (математик, специалист по теории представлений и матфизике) понимаю — да. С другой стороны, «палечные» методы тоже могут быть достаточно точными. Пример.
Ищем число 5 в упорядоченном списке длины N.
Алгоритм 1: Тупо перебираем все элементы «он.не он». Если 5 окажется в самом конце списка, мы сделали N операций.
Значит, быстрота алгоритма O(N).
Алгоритм 2: Действуем по принципу «лев в пустыне» — список-то упорядоченный! — делим пустыню пополам, в одной половине лев есть, в другой — нет. Делим список пополам, смотрим на конечные значения. Если 5 между ними — это наш новый список.
За K шагов алгоритма список стал в 2^K раз короче, значит, когда 2^K = N, у нас только 1 элемент, и дело сделано за K = logN шагов. Быстрота алгоритма = O(logN).
А с формулами туго, что ты в них подставишь?
Интересно, а есть на форуме профессиональные программисты. Занятно было бы услышать профессиональную оценку моего бреда… 🙂
Good Luck,
UT
Поскольку я недопрограммист, а студент…счтитайте что дальше идут стендартные отмазки…
ИМХО, алгоритмизация подстчета для 1 и 2, сильно различны, поскольку количество итераций как таковых мало влияет на время работы процесса этого алгоритма. Пример
десять раз сложить — это быстрее, чем 5 раз умножить.
Так как по представлению сложениесдвиг и оценки погрешности при переносе разрядов — Умножение в 2 раза медленее. Так же если представленна система команд процессора на умножение(например в архитектуре CISC) то это не ускорит процесс, а скорее увеличит время на выборку адресса инструкции(Схемотехника фарево).
Честно говоря не знаю на сколько уменьшение кол-ва итераций увеличит скорость работы, ведь и степень и логарифм долие для получения двоично-десятичного кода, а следовательно примерно одинаковы по скорости, хотя степень быстрее, но обработка склаживает…разницу. А в матеиатическом представлении — да….наверное, алгоритм 2 быстрее. Хотя я себе туго представляю подсчет «O»…. Но на уровне тактов процессора, ИМХО оба метода примерно равны по скорости (+-100 нс.)
anonymous 22:27, 29 февраля 2004
Ну да, это понятно. Именно поэтому в обозначениях «О большое». Т.е., оценка дается не бестродействию алгоритма в сравнении с другими для того же N, а тому, как время его выполнения растет с ростом N.
Если, скажем, f(N) = O(N); g(x) = O(N^2), то ничего невозможно сказать про то, что больше, f(25) или g(25) — или любого другого конкретного N. Единственное, что можно сказать, это что если N увеличить в два раза, то f возрастет в 2 раза, а g возрастет в 4 раза.
«O большое» не подсчитывается. По определению,
где C — произвольная константа, от x не зависящая. В контексте обсуждаемой проблемы — в нее идет время выполнения одной итерации. Разумеется, для разных алгоритмов она разная, поэтому сравнивать разные алгоритмы на этом основании нельзя.
ЗЫ А чей-то ты выкать начал? 😉
Longobard 23:26, 29 февраля 2004
Uncle Theodore
Ну да, это понятно. Именно поэтому в обозначениях «О большое».
Т.е., оценка дается не бестродействию алгоритма в сравнении с другими для того же N, а тому, как время его выполнения растет с ростом N.
Если, скажем, f(N) = O(N); g(x) = O(N^2), то ничего невозможно сказать про то, что больше, f(25) или g(25) — или любого другого конкретного N. Единственное, что можно сказать, это что если N увеличить в два раза, то f возрастет в 2 раза, а g возрастет в 4 раза.
«O большое» не подсчитывается. По определению,
O(x) = Cx
где C — произвольная константа, от x не зависящая. В контексте обсуждаемой проблемы — в нее идет время выполнения одной итерации. Разумеется, для разных алгоритмов она разная, поэтому сравнивать разные алгоритмы на этом основании нельзя.
Good Luck,
UT
ЗЫ А чей-то ты выкать начал? 😉
Хорошо объяснил. Понятно. Спасибо. А вникать я начал потому что хочу узнать. Потому что любознательный. Узнал что есть такая весчь «оченка времени работы алгоритма», узнал что она выглядит так.
Теперь вникаю благодаря UT как ее осущетвлять.
ЗЫ: UT, а ты преподом чтоль работаешь? А то очень хорошо объясняешь.
Longobard 23:26, 29 февраля 2004
Uncle Theodore
Ну да, это понятно. Именно поэтому в обозначениях «О большое».
Т.е., оценка дается не бестродействию алгоритма в сравнении с другими для того же N, а тому, как время его выполнения растет с ростом N.
Если, скажем, f(N) = O(N); g(x) = O(N^2), то ничего невозможно сказать про то, что больше, f(25) или g(25) — или любого другого конкретного N. Единственное, что можно сказать, это что если N увеличить в два раза, то f возрастет в 2 раза, а g возрастет в 4 раза.
«O большое» не подсчитывается. По определению,
O(x) = Cx
где C — произвольная константа, от x не зависящая. В контексте обсуждаемой проблемы — в нее идет время выполнения одной итерации. Разумеется, для разных алгоритмов она разная, поэтому сравнивать разные алгоритмы на этом основании нельзя.
Good Luck,
UT
ЗЫ А чей-то ты выкать начал? 😉
Просто интересно. Учиться всегда интересно :).
ЗЫ: а ты случайно не преподом работаешь? А то очень ъхорошо объясняешь. Понятно и четко.
decvar 00:13, 1 марта 2004
ЗЫ А чей-то ты выкать начал? 😉
anonymous 00:13, 1 марта 2004
LONGOBARD
Просто интересно. Учиться всегда интересно :).ЗЫ: а ты случайно не преподом работаешь? А то очень ъхорошо объясняешь. Понятно и четко.
Я ж говорил, я — профессор математики в одном американском университете, учу детей математике уже девять лет, начинал в Новосибирском Универе… Эх, какие у меня там студенты были, не то, что на этой помойке пяти континентов… Ну это уже офтоп пошел. Хотя да, разбираться всегда интересно.
Longobard 16:52, 1 марта 2004
Понятно теперь почему ты такой умный 🙂 А не мог бы еще написать свои суждения на эту тему? Дополнить картину так сказать. Например как мне рассчитать быстродействие бинарного поиска? На мой взгляд оно где-то в районе О(N^3). Я правильно посчитал? (N-длина массива).
anonymous 17:39, 1 марта 2004
М-м-м… Что ты называешь бинарным поиском? Классический бинарный поиск — это Алгоритм 2 в моем примере (лев в пустыне). И он O(logN)…
Genie 13:54, 18 марта 2004
Мда, как жалко, что я так редко заглядываю в раздел программирование :)))
Наверное потому, как врядли тут увижу интересное мне логическое программирование (ну или декларативное), поскольку вещи эти несколько иррациональны с точки зрения прикладного программирования..
Но тем не менее, оценка времени выполнения программы производится на двух этапах.
Алгоритмическом и программном. Хотя это уже упоминалось 🙂
Первое, алгоритмическое, имеет более сильное влияние на время выполнения программы, поскольку именно тут можно сократить порядок выполнения операций, и, в большинстве случаев, это наиболее лёгкая оценка времени выполнения программы.
Программная производится гораздо реже, и уже намного после выполнения оценки алгоритмической сложности.
Возьмём тот же самый поиск простых чисел. И для него рассмотрим несколько алгоритмов.
(почему-то так получилось, что на днях я наткнулся на одну из своих программок именно по поиску этих самых чисел, и в памяти много чего повылазило)
Исходно, ограничимся поиском всех простых чисел, вмещающихся в unsigned long, до 4′294′967′295.
Алгоритм. Тупой до безобразия. Берём следующее число, тупо проверяем его делимость на все предыдущие и выводим его, если оно-таки простое. Сложность сего алгоритма для отдельного числа — O(N), для всего — O(N^2). Итого для случая поиска до 2^32-1 (4′294′967′295) получаем где-то в районе «O»(2^64).
А это, емнип, всего-то навсего «O»(18′446′744′073′709′551′616). Помрём, пока дождёмся :))
Упрощение 1. Нафига проглядывать все числа, если заведомо все чётные, кроме 2 — непростые? O(N) на число, и всё то же O(N^2) на весь алгоритм. Быстрее, конечно, чем без упрощения, но роли не играет.. Разиков эдав в 8 меньше..
Упрощение 2. Зачем пытаться делить на числа, бОльшие, чем корень_из(N)? О! вот тут качественный скачок — для одного числа — O(корень(N)), алгоритма — O(N^1.5). Итого будет порядка «O»(2^48) — а это уже получше..
Казалось бы, на этом и всё.. Однако, всё же есть и дальнейшее упрощение.
Упрощение 3. Нет необходимости делить на все нечётные числа, меньшие корня_из(N). Можно делить только на те, ято являются простыми. Так что там у нас со сложностью для одного отдельно взятого числа? O(число_простых_чисел_не_больших_корня_из(N)). Возникает вопрос, а сколько это? То, что это меньше, чем O(корень(N)), это так.
Я бы сказал, что это o(log(N)), но доказательства строгого — нет. И общее будет o(N*log(N)). В том-то и дело, что «o», а не «O»!!
Источник: www.nixp.ru