Программа последовательность чисел фибоначчи

Иногда полезно реализовать собственный тип последовательности, у которого есть функции, аналогичные встроенным функциям для кортежей или списков.

Как вы уже знаете, последовательность может быть изменяемой или неизменяемой. В этой статье мы сосредоточимся на создании пользовательского неизменяемого типа последовательности.

У неизменяемой последовательность должно быть две основные возможности:

• Возвращать количество элементов последовательности.
• Возвращать элемент по заданному индексу или вызывать ошибку IndexError, если индекс выходит за границы последовательности.

Если объект удовлетворяет вышеуказанным требованиям, получится производить следующие действия:

• Использовать синтаксис квадратных скобок [] для получения элемента по индексу.
• Перебирать элементы последовательности: например, с помощью цикла for.

Чтобы реализовать перечисленные выше возможности, нужно создать следующие методы:

• __getitem__ — возвращает элемент по заданному индексу.
• __len__ — возвращает длину последовательности.

1) Метод __getitem__

У метода __getitem__ должен быть аргумент index , который является целым числом. Метод __getitem__ должен вернуть элемент из последовательности на основе указанного индекса.

Как вывести последовательность чисел Фибоначчи на Python?

Диапазон значений index : от нуля до length — 1 . Если индекс выходит за границы, метод __getitem__ должен выдать исключение IndexError.

Метод __getitem__ может принимать объект среза для слайсинга.

2) The __len__ method

Если у пользовательской последовательности есть метод __len__ , вы можете использовать встроенную функцию len() , чтобы получить количество элементов последовательности.

Последовательность Фибоначчи

Последовательность Фибоначчи примерно в 1170 году открыл Леонардо Фибоначчи, итальянский математик.

В последовательности Фибоначчи каждое число является суммой двух предшествующих ему чисел. Например:

1, 1, 2, 3, 5, 8 , 13, 21, .

Последовательность Фибоначии можно задать следующей формулой:

f(1) = 1
f(2) = 1
f(n) = f(n-1) + f(n-2) если n > 2

В некоторые источниках сказано, что последовательность Фибоначчи начинается с нуля, а не с 1, как сейчас. То есть вот так:

0, 1, 1, 2, 3, 5, 8 , 13, 21, .

Но мы будем придерживаться исходной последовательности Фибоначчи, которая начинается с единицы.

Чтобы вычислить число Фибоначчи в Python, нужно создать такую рекурсивную функцию:

def fib(n): if n < 2: return 1 return fib(n-2) + fib(n-1)

В этой рекурсивной функции fib(1) и fib(2) всегда возвращают 1. А когда n больше 2, fib(n) = fib(n-2) — fib(n-1) .

Добавим print() в начало функции, чтобы посмотреть, как она работает, и вызовем функцию fib() с аргументом 6.

def fib(n): print(f’Считаю число Фибоначчи’) if n < 2: return 1 return fib(n-2) + fib(n-1) fin(6)

Вывод

Считаю 6 число Фибоначчи
Считаю 4 число Фибоначчи
Считаю 2 число Фибоначчи

Числа Фибоначчи. Решение задачи на Python

Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 5 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 4 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи

Как вы видите, функция fib() часто повторяется.

Например, ей приходится трижды вычислять 3 число Фибоначчи. Это неэффективно.

Чтобы решить эту проблему, в Python есть декоратор под названием lru_cache из модуля functools .

lru_cache позволяет кэшировать результат работы функции. Когда вы передаете тот же аргумент функции, функция просто получает результат из кэша вместо того, чтобы пересчитывать его.

Ниже показано, как использовать декоратор lru_cache для ускорения работы функции fib() :

Вывод

Считаю 6 число Фибоначчи
Считаю 4 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 5 число Фибоначчи

Как вы видите, количество вычислений значительно уменьшилось.

Создаем последовательность Фибоначии

1. Сначала определим класс, реализующий последовательность Фибоначчи:

class Fibonacci: def __init__(self, n): self.n = n

Метод __init__ принимает целое число n , которое задает длину последовательности.

2. Теперь определим статический метод, который вычисляет значение определенного числа Фибоначчи:

3. Реализуем метод __len__ , чтобы мы могли использовать встроенную функцию len() для получения количества элементов из последовательности Фибоначчи:

def __len__(self): return self.n

4. Реализуем метод __getitem__ для поддержки индексации с помощью синтаксиса квадратных скобок []:

def __getitem__(self, index): if isinstance(index, int): if index < 0 or index >self.n — 1: raise IndexError return Fibonacci.fib(index)

Метод __getitem__ принимает целое число index. Метод __getitem__ проверяет, является ли индекс целым числом, используя функцию isinstance() .

Если index выходит за границы последовательности, __getitem__ вызовет исключение IndexError. В противном случае он вернет число Фибоначчи индекса.

Соединим все вместе:

Кастомная последовательность Фибоначчи в виде Python-класса готова. Однако вы не сможете просто сохранить этот код в модуле fibonacci.py и использовать его в другом скрипте.

Давайте разберемся, как использовать созданную последовательность.

Используем последовательность Фибоначии

Ниже показано, как использовать последовательность Фибоначчи из модуля fibonacci.py :

from fibonacci import Fibonacci fibonacci = Fibonacci(10) # используем [] print(‘Используем последовательность Фибоначчи с помощью []:’) print(fibonacci[0]) print(fibonacci[1]) print(fibonacci[2]) print(‘Используем последовательность Фибоначчи с помощью цикла for:’) # используем for for f in fibonacci: print(f)

Вывод

Используем последовательность Фибоначии с помощью []:
1
1
2
Используем последовательность Фибоначчи с помощью цикла for:
1
1
2
3
5
8
13
21
34
55

Как это работает

1. Создаем новый экземпляр последовательности Фибоначчи, в котором содержится 10 элементов.
2. Получаем доступ к элементам последовательности Фибначчи с помощью квадратных скобок [].
3. Используем последовательность Фибоначии в цикле for.

Добавляем поддержку срезов

Чтобы можно было делать срезы нашей последовательности, как показано ниже,

fibonacci[1:5]

. нужно добавить соответсвующую логику, которая будет обрабатывать объект среза.

В fibonacci[1:5] аргументом index метода __getitem__ является объект среза, начало которого равно 1, а конец — 5.

Вы можете использовать метод indices() объекта среза, чтобы получить индексы элементов для возврата из последовательности:

indices = index.indices(self.n)

self.n — это длина последовательности, которая будет «нарезана». В данном случае это количество элементов в последовательности Фибоначчи.

Чтобы вернуть список Фибоначчи из среза, вы можете передать индексы в функцию range() и сделать вот так:

[Fibonacci.fib(k) for k in range(*indices)]

Соберем все вместе:

Теперь можно сделать срез последовательности следующим образом:

from fibonacci import Fibonacci fibonacci = Fibonacci(10) print(fibonacci[1:5])

Вывод

[1, 2, 3, 5]

Что нужно запомнить

• Для создания кастомной последовательно нужно реализовать методы __len__ и __getitem__ .
• Метод __getitem__ должен возвращать элемент по заданному индексу или вызывать ошибку IndexError, если индекс выходит за границы последовательности.

СodeСhick.io — простой и эффективный способ изучения программирования.

Источник: codechick.io

Ряд Фибоначчи и Мемоизация с примерами на Swift языке

Чи́сла Фибона́ччи (вариант написания — Фибона́чи [2] ) — элементы числовой последовательности

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, … (последовательность A000045 в OEIS),

в которой первые два числа равны 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел [3] . Названы в честь средневекового математика Леонардо Пизанского (известного как Фибоначчи) [4] .

— Википедия

Ряд Фибоначчи часто упоминается на собеседованиях, потому что в нем демонстрируется множество мощных методов, включая рекурсию. Он является отличным примером того, что мы называем мемоизацией(запоминанием). Понимание ряда Фибоначчи и его работы очень полезно.
Математически ряд Фибоначчи представляет собой последовательность чисел, которые следуют этому уравнению: F(n) = F(n-1) + F(n-2). Эта последовательность встречается в различных интересных контекстах, например, в природе, в раковинах, спиральных структурах и галактиках, а также в дизайне римских полов, и даже брокеры используют ряд Фибоначчи для прогнозирования акций.

func fib(_ n: Int) -> Int < if n == 0 < return 0 >else if n == 1 < return 1 >else < return fib(n — 1) + fib(n — 2) >>

В коде серия Фибоначчи выглядит следующим образом: для F(0) и F(1) возвращаем их значения напрямую, а затем алгоритм сводится к этой строке — return fib(n-1) + fib(n-2). Это является ключевым моментом алгоритма и демонстрирует использование рекурсии.
Однако у ряда Фибоначчи есть проблема: с увеличением чисел в последовательности алгоритм требует все больше времени для вычисления. Это связано с тем, что время, необходимое для вычислений, растет экспоненциально, и сложность алгоритма составляет O(2^n). Это делает вычисления очень затратными.
Наша задача — найти способ оптимизировать этот алгоритм и сделать его быстрее. Именно здесь на помощь приходит мощная техника, известная как мемоизация, которую важно знать и понимать.

Мемоизация

Чтобы понять мемоизацию, нужно рассмотреть проблему с рядом Фибоначчи. Для простых чисел, таких как число до F(5), ряд Фибоначчи вычисляется достаточно быстро. Однако, при вычислении чисел более высокого порядка, повторное вычисление чисел становится очень затратным по времени.

Мемоизация — это техника оптимизации, ускоряющая алгоритмы за счет кэширования или хранения результатов вычислений для их использования в будущих вычислениях. В случае ряда Фибоначчи, мы можем создать словарь (назовем его «Memo») для хранения ранее вычисленных чисел. Затем, когда мы вычисляем каждое число ряда Фибоначчи, мы сохраняем результат в массиве и возвращаем его. Таким образом, в следующий раз нам не нужно вычислять это число снова и снова.

var memo = [Int: Int]() func fib(_ n: Int) -> Int < if n == 0 < return 0 >else if n == 1 < return 1 >if let result = memo[n] < return result >memo[n] = fib(n — 1) + fib(n — 2) return memo [n]! >

Благодаря мемоизации, эффективность алгоритма возрастает значительно. Теперь вместо того, чтобы за 19 секунд вычислить ряд Фибоначчи из 30 чисел, мы можем вычислить тысячи чисел. Это увеличение на 3333%. Мы превратили алгоритм из экспоненциального (O(2^n)) в линейный (O(n)).

Именно поэтому ряд Фибоначчи и мемоизация являются отличными примерами для интервью. Они объединяют рекурсию и мемоизацию, показывая, как сделать затратный алгоритм быстрее. Знание и понимание ряда Фибоначчи и мемоизации помогут вам решать подобные задачи быстро и эффективно.

import UIKit func fibNaive(_ n: Int) -> Int < print(n) if n == 0 < return 0 >else if n == 1 < return 1 >else < return fibNaive(n — 1) + fibNaive(n — 2) >> fibNaive(20) // 20 = 13s / 22 = 54 s var memo = [Int: Int]() func fib(_ n: Int) -> Int < if n == 0 < return 0>else if n == 1 < return 1 >if let result = memo[n] < return result >memo[n] = fib(n — 1) + fib(n — 2) return memo[n]! > fib(22) // 90 max

Что касается создания одного из них с нуля, то это очень просто. Представляю к вашему вниманию две реализации: одну наивную, которая ничего не запоминает и не хранит, и вторую, где мы используем мемоизацию и храним наши результаты по мере их вычисления.

На мгновение остановимся на мемоизированном варианте, чтобы показать, сколько времени требуется для выполнения очень маленького вычисления Фибоначчи для числа 20. Если мы запустим его для простого числа, например, 20, вы увидите, что счетчик работает, пересчитывая одни и те же числа снова и снова. В среднем это занимает около 13 секунд, что не так уж и много.

Теперь, если я увеличу его на один или два, это займет еще больше времени. Это экспоненциальный рост, увеличивающийся в размерах, и для очень маленьких приращений числа требуется все больше и больше времени. Именно так работает ряд Фибоначчи, и именно поэтому он так затратен.

Теперь давайте сравним это с мемоизированной версией и посмотрим, каково это — хранить эти значения. Во втором случае мы будем хранить наши результаты в словаре. Каждый раз, когда мы вычисляем F(n-1) + F(n-2), мы будем хранить его в ключе, представленном N, каким бы ни было число в этот момент (20, 21, 22 и т. д.). Мы просто сохраним этот результат. Затем, по мере выполнения последовательных вычислений, если мы можем извлечь результат из словаря, мы просто вернем его, не вычисляя его снова.

Заключение:

Это удобно не только для рядов Фибоначчи, но и для всего, что связано с дорогостоящими вычислениями, которые можно сохранить, кэшировать и использовать в будущих результатах.

В этом и заключается сила мемоизации.

Она используется для самых разных вещей.

Ряд Фибоначчи — отличный пример. Когда дело доходит до реального интервью.

Я слышал, как людей просили воспроизвести ряд Фибоначчи.

Это не огромный алгоритм, он сводится к одной строчке и двум случаям: конец равен нулю и единице. Но мой совет — просто запомните эту строчку, потому что она демонстрирует такую вещь как рекурсия.

Как только вы это поймете, очень просто перейти к мемоизированному примеру, где вы сможете продемонстрировать как взять трудозатратный алгоритм и сделать его более эффективным. Вы знаете — это называется мемоизацией.

Источник: habr.com

Вычисление чисел Фибоначчи

Числа Фибоначчи — это числа такой последовательности, в которой первые два элемента — 0 и 1, а каждый последующий элемент равен сумме двух предшествующих. Выглядит это так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …

Примечание Иногда 0 опускается, и в этом случае ряд начинается с 1, но мы будем использовать последовательность с 0 на первой позиции.

Формула записывается следующим образом:

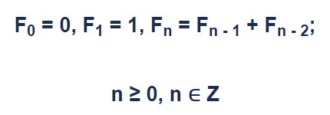
Вычисление ряда Фибоначчи — стандартная задача, которую задают на собеседованиях, чтобы проверить кандидата на понимание алгоритмов. Не так популярна, как сортировка, но всё же.

Давайте вычислим ряд и его отдельные элементы, использовав для этого язык Java.

Вычислить ряд Фибоначчи циклом

Предположим, что нам нужно вывести на экран первые десять чисел последовательности Фибоначчи. Мы помним, что:

• первый элемент ряда — 0, второй — 1;
• каждый последующий — сумма двух предыдущих.

Тогда наша последовательность будет иметь такой вид:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34

Но нам нужно вывести результат с использованием программы. Держите код с объяснениями в комментариях:

public class Main < public static void main(String[] args) < //Объявляем переменные при известных первых двух: int num0 = 0; int num1 = 1; int num2; //Первые две переменные выводим вне цикла: System.out.print(num0 + » » + num1 + » «); for(int i = 3; i > >

Выполнение завершится на десятом элементе. Количество элементов при этом можно менять, изменив значение в условиях цикла.

Найти число Фибоначчи через рекурсию

Рекурсивная функция — это такая функция, которая вызывает саму себя. Она также неплохо отрабатывает в алгоритмических задачах вроде чисел Фибоначчи, но ей требуется больше времени.

Почему так происходит? Всё дело в том, что рекурсивная функция приводит к многоразовому вызову одних и тех же операций. Именно из-за этого её не рекомендуется использовать, но если уж на собеседовании прозвучит такая задача, вы будете готовы.

Рассмотрим пример, в котором нам нужно получить n-ое число в ряде Фибоначчи:

public int fibonacciValue(num) < if (num else if (num == 2) < return 1; >else < return fibonacciValue(num — 1) + fibonacciValue(num — 2); >>

Если в качестве num задать большое значение, программа зависнет.

Тип int в Java может хранить значения до 2147483647, так что вычислить получится лишь первые 46 чисел Фибоначчи. Тип long хранит до 9223372036854775807, а это 91 число Фибоначчи. Класс BigInteger призван работать с действительно большими значениями, вот только само выполнение программы это никак не ускорит.

Использовать для вычисления Stream

Stream в Java — это компонент для самостоятельной внутренней итерации своих же элементов. Подробнее о нём вы можете почитать в нашей статье о Java Stream API.

И, разумеется, Stream подходит для вычисления элементов последовательности Фибоначчи:

Stream.iterate(new int[], arr -> new int[]) //Задаём лимит значений: .limit(num) //Отбираем по первому элементу каждого массива: .map(y -> y[0]) //Выводим в консоль: .forEach(x -> System.out.println(x));

В данном примере метод iterate() будет возвращать упорядоченный поток, ограниченный лимитом в num значений и созданный с применением функции к начальному массиву arr . В консоль будет выведено следующее:

А так мы получим сумму чисел последовательности по элемент num включительно:

int fibonacciValuesSum = Stream.iterate(new int[], arr -> new int[]) .limit(num) .map(y -> y[0]) .mapToInt(Integer::intValue) .sum(); System.out.println(fibonacciValuesSum);

Математический тест

Любите математику? Попробуйте решить наш математический тест:

Источник: tproger.ru