Программа полином что это

Программа полином что это

Построение корректирующих (помехоустойчивых) кодов основано на операциях с образующими полиномами. Для поиска образующих полиномов, необходимых для построения кодов, более эффективных, чем укороченные БЧХ-коды, требуются большие вычислительные затраты. В данной статье приведена программная реализация алгоритма поиска образующих полиномов с применением технологий параллельных и распределённых вычислений, в частности OpenMP и MPI. Проведено исследование по быстродействию программных реализаций при различных входных параметрах m и t. Представлены результаты по времени поиска образующих полиномов с входными параметрами m от 16 до 24, t = 3 и t = 4, объясняющие целесообразность применения технологий OpenMP и MPI. Было установлено, что при использовании 30 ядер распределённой системы (суперкомпьютерный кластер) среднее ускорение для m от 16 до 24 и t = 4 составляет около 3900 %, при этом поиск можно ускорить, используя больше ресурсов (количество ядер) кластера.

Полином

программная реализация
распределённые вычисления
параллельные вычисления
образующий полином
помехоустойчивый код

2. Антонов А.С. Параллельное программирование с использованием технологии OpenMP: учебное пособие. – М.: Изд-во МГУ, 2009. – 77 с.

3. Антонов А. С. Параллельное программирование с использованием технологии MPI: учебное пособие.¬ – М.: Изд-во МГУ, 2004. – 71 с.

4. Боуз Р.К., Рой-Чоудхури Д.К. Об одном классе двоичных групповых кодов с исправлением ошибок // Кибернетика. – М., 1964. – С. 112-118.

5. Мальчуков А.Н. Алгоритмическое и программное обеспечение системы для разработки кодеков помехоустойчивых кодов: дисс. … канд. техн. наук: 05.13.11 / Мальчуков Андрей Николаевич: [Место защиты: Том. политехн. ун-т]. – Томск, 2008. – C. 50-51: ил. РГБ ОД, 61 09-5/472.

7. СКИФ-1. Center of supercomputing. 2013. URL: http://cluster.tpu.ru/?q=node/26 (дата обращения: 01.10.2014).

При построении популярных блоковых помехоустойчивых кодов (Боуза – Чоудхори –Хоквингема (БЧХ-кодов), Рида – Соломона) используются полиномы Жегалкина. БЧХ-коды [4] имеют чёткие рекомендации выбора образующего полинома, но такие коды ограничены фиксированной длиной кодового слова.

Остальные длины кодовых слов получаются путём укорачивания более длинных кодовых слов за счёт уменьшения разрядности информационного блока при сохранении количества контрольных разрядов. Укорачивание БЧХ-кодов вводит лишнюю избыточность, которая не несёт в себе дополнительных корректирующих возможностей, а лишь уменьшает эффективность кода.

При поиске образующих полиномов, необходимых для построения кодов, более эффективных, чем укороченные БЧХ-коды, известны только необходимые начальные условия для поиска, такие как минимальные вес образующего полинома, минимальная длина кодового слова, а значит, и минимальная длина образующего полинома. Для того чтобы найти подходящий полином, необходимо перебрать все полиномы, подходящие под выше озвученные необходимые условия, и, если среди них не найдётся полином, который будет удовлетворять достаточным условиям, то поиск продолжится среди полиномов, длина которых на единицу больше, чем предыдущих [5]. В связи с приведёнными необходимыми и достаточными условиями задача по поиску образующего полинома является достаточно трудоёмкой. Таким образом, чтобы значительно ускорить выполнение данной задачи, следует применять технологии параллельных и распределённых вычислений.

Полиноми

Алгоритм поиска образующих полиномов

Алгоритм поиска образующих полиномов заключается в полном переборе всех полиномов – претендентов и проверке их на выполнение достаточных [1, 5] условий, что является ресурсоемкой задачей. Среди достаточных условий образующего полинома являются два основных: 1) строящийся на основе этого образующего полинома код должен иметь расстояние Хэмминга не меньшее, чем d=2t+1; 2) остатки от деления всех комбинаций ошибок на образующий полином в рамках заданной t должны быть уникальными. Полное описание алгоритма поиска образующих полиномов приведено в [5].

Для поиска образующего полинома задаются входные параметры, такие как: разрядность информационного блока (m) и количество исправляемых независимых ошибок (t). Выходным значением является образующий полином в двоичном представлении.

При анализе алгоритма поиска образующего полинома было установлено, что при больших значенияx входного параметра m значительное время работы алгоритма занимает вычисление расстояния Хэмминга помехоустойчивого кода, а также при увеличении значений входного параметра t увеличивается время проверки синдромов на уникальность.

Для анализа возможности распараллеливания программа была условно разбита на 2 этапа, с замером времени выполнения для каждого этапа. Первым этапом является проверка расстояния Хэмминга, второй этап – проверка синдромов ошибок на уникальность. Анализ алгоритма показал, что при поиске образующего полинома практически все полиномы-кандидаты проходят через первый этап, в то время как через этап проверки синдромов на уникальность проходит 1–2 полинома, которые, как правило, являются образующими. Таким образом, в данном алгоритме этап проверки расстояния Хэмминга требует временных затрат за счет большого количества проверяемых полиномов, в то время как второй этап требует временных затрат для проверки каждого полинома из множества [6].

Из анализа можно сделать вывод, что для достижения наилучшей оптимальности следует использовать технологию MPI в совокупности с OpenMP. Так, технологию OpenMP с распараллеливанием вычислений на потоки можно в данном случае применить для оптимизации этапа проверки синдромов на уникальность, а технология MPI позволит оптимизировать этап проверки расстояния Хэмминга за счет распределения большого числа проверяемых полиномов на группы для уменьшения области перебора.

Применение технологий OpenMP и MPI для поиска образующего полинома

Для увеличения быстродействия поиска образующего полинома были применены технологии параллельных и распределённых вычислений, такие как OpenMP [2] и MPI [3]. С использование технологии OpenMP был оптимизирован этап проверки синдромов ошибок на уникальность [1].

При использовании технологии MPI осуществляется межпроцессорный обмен полиномами заданной длины и веса в распределённой системе (суперкомпьютерный кластер) [7]. Главный процессор с помощью команды MPI_Send пересылает списки полиномов другим процессорам, которые принимают данные с помощью команды MPI_Recv и осуществляют поиск образующего полинома среди принятого набора.

В случае если среди полиномов заданной длины и веса образующий полином не найден, то согласно алгоритму поиска [5] увеличивается вес полинома, и обмен сообщений между процессорами повторяется. Если же вес полинома становится равным его длине, а полином не найден, то длина полинома-кандидата увеличивается на единицу и поиск осуществляется среди нового набора кандидатов. На рис. 1 приведена схема применения технологий OpenMP и MPI для задачи поиска образующего полинома.

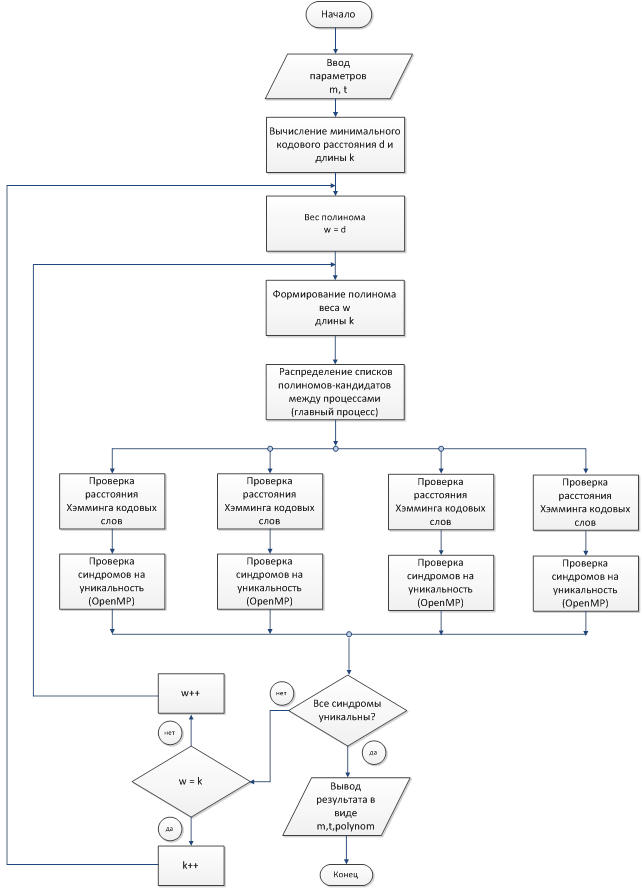
Рис. 1. Схема применения OpenMP и MPI для поиска образующего полинома

Результаты компьютерного эксперимента по поиску образующих полиномов

Для получения статистики по времени поиска образующих полиномов было произведено по 20 запусков исполняемого файла программы, разработанной с применением технологий OpenMP и MPI, на процессорах Intel XEON 5150 2.66Ghz. Для компьютерного эксперимента входной параметр m (длина информационного блока) был выбран в диапазоне от 16 до 24, а параметр t (кратность исправляемых ошибок) равным 3 и 4.

Далее представлены результаты по времени поиска образующего полинома с применением технологии MPI при использовании 30 ядер процессора Intel XEON 5150 в распределённой системе (суперкомпьютерный кластер). В таблице 1 приведены средние значения по времени поиска образующего полинома (с доверительными интервалами) с применением технологий OpenMP и MPI на 30 ядрах процессора Intel XEON 5150 2.66Ghz.

Средние значения по времени поиска образующего полинома с применением OpenMP и MPI для t = 3 с доверительными интервалами в %

MPI + OpenMP (30 ядер), c, (%)

Источник: science-education.ru

Интерполяция каноническим полиномом

Интерполяция — приближение одной функции другой функцией.

С самого начала хотелось бы заметить, что мы занимаемся интерполяцией функций, а не узлов. Разумеется, интерполяция будет проводиться в конечном числе точек, но выбирать их мы будем сами.

В настоящем исследовании будет изучена проблема интерполяции функции одной переменной полиномом каноническим полиномом, будет рассмотрен вопрос точности приближения, и как, варьируя узлы, через которые пройдёт полином, достигнуть максимальной точности интерполяции.

Полином в каноническом виде

Известно, что любая непрерывная на отрезке [a,b] функция f(x) может быть хорошо приближена некоторым полиномом Pn(x). Справедлива следующая Теорема (Вейерштрасса): Для любого >0 существует полином Pn(x) степени , такой, что

В качестве аппроксимирующей функции выберем полином степени n в каноническом виде:

Коэффициенты полинома определим из условий Лагранжа , , что с учётом предыдущего выражения даёт систему линейных алгебраических уравнений с n+1 неизвестными:

Обозначим систему таких уравнений символом (*) и перепишем её следующим образом:

или в матричной форме: где — вектор-столбец, содержащий неизвестные коэффициенты , — вектор-столбец, составленный из табличных значений функции , а матрица имеет вид:

Система линейных алгебраических уравнений (*) относительно неизвестных иметь единственное решение, если определитель матрицы отличен от нуля.

Определитель матрицы называют определителем Вандермонда, его можно вычислить по следующей формуле:

Число узлов интерполяционного полинома должно быть на единицу больше его степени. Это понятно из интуитивных соображений: через 2 точки можно провести единственную прямую, через 3 — единственную параболу и т.д. Но полином может получиться и меньшей степени. Т.е. если 3 точки лежат на одной прямой, то через них пройдёт единственный полином первой степени (но это ничему не противоречит: просто коэффициент при старшей степени равен нулю).

При достаточной простоте реализации метода он имеет существенный недостаток: число обусловленности матрицы быстро растёт с увеличением числа узлов интерполяции, что можно показать на следующем графике

Из-за плохой обусловленности матрицы рекомендуется применять другие методы интерполяции (например, интерполяция полиномами Лагранжа). При этом важно понимать, что при теоретическом применении различных методов они приводят к одинаковому результату, т.е. мы получим один и тот же полином.

Однако при практической реализации мы получим полиномы различной точности аппроксимации из-за погрешности вычислений аппаратуры.

Способ вычисления полинома в точке

Чтобы изобразить графически аппроксимирующий полином, необходимо вычислить его значение в ряде точек. Это можно сделать следующими способами.

Первый способ. Можно посчитать значение a1x и сложить с a0. Далее найти a2x 2 , сложить с полученным результатом, и так далее. Таким образом, на j-ом шаге вычисляется значение ajx j и складывается с уже вычисленной суммой .

Вычисление значения ajx j требует j операций умножения. Т.е. для подсчёта многочлена в заданной точке требуется (1 + 2 + . + n) = n(n+1)/2 операций умножения и n операций сложения. Всего операций в данном случае: Op1 = n(n+1)/2 + n.

Второй способ. Полином можно также легко вычислить с помощью так называемой схемы Горнера:

Для вычисления значения во внутренних скобках anx + an-1 требуется одна операция умножения и одна операция сложения. Для вычисления значения в следующих скобках (anx + an-1)x + an-2 требуется опять одна операция умножения и одна операция сложения, т.к. anx + an-1 уже вычислено, и т.д.

Тогда в этом способе вычисление Pn(x) потребует n операций умножения и n операций сложения, т.е. сложность вычислений Op2 = n+n = 2n. Ясно, что Op2 1.

Анализ метода

Сложность вычислений

Оценка сложности интерполирования функции складывается из количества операций для решения системы линейных алгебраических уравнений (СЛАУ) и нахождения значения полинома в точке.

Сложность решения СЛАУ, например, методом Гаусса для матрицы размера nxn: 2n 3 /3, т.е. O(n 3 ).

Для нахождения полинома в заданной точке требуется n умножений и n сложений. В результате сложность метода: O(n 3 ).

Погрешность интерполяции

Предположим, что на отрезке интерполирования [a,b] функция f(x) n раз непрерывно-дифференцируема. Погрешность интерполяции складывается из погрешности самого метода и ошибок округления.

Ошибка приближения функции f(x) интерполяционным полиномом n-ой степени Pn(x) в точке x определяется разностью: Rn(x) = f(x) — Pn(x).

Погрешность Rn(x) определяется следующим соотношением:

Здесь — производная (n+1)-го порядка функции f(x) в некоторой точке а функция определяется как

Если максимальное значение производной f n+1 (x) равно то для погрешности интерполяции следует оценка:

При реализации данного метода на ЭВМ ошибкой интерполяции En(x) будем считать максимальное уклонение полинома от исходной функции на выбранном промежутке:

Выбор узлов интерполяции

Ясно, что от выбора узлов интерполируемой функции напрямую зависит, насколько точно многочлен будет являться её приближением.

Введём следующее определение: полиномом Чебышева называется многочлен вида

Известно (см. ссылки литературы), что если узлы интерполяции x0, x1. xn являются корнями полинома Чебышева степени n+1, то величина принимает наименьшее возможное значение по сравнению с любым другим выбором набора узлов интерполяции.

Очевидно, что в случае k = 1 функция T1(x), действительно, является полиномом первой степени, поскольку T1(x) = cos(arccos x) = x.

В случае k = 2 T2(x) тоже полином второй степени. Это нетрудно проверить. Воспользуемся известным тригонометрическим тождеством: cos2θ = 2cos²θ — 1, положив θ = arccos x.

Тогда получим следующее соотношение: T2(x) = 2x² — 1.

С помощью тригонометрического тождества cos(k + 1)θ = 2cosθcoskθ — cos(k — 1) легко показать, что для полиномов Чебышева справедливо реккурентное соотношение:

При помощи данного соотношения можно получить формулы для полиномов Чебышева любой степени.

Корни полинома Чебышева легко находятя из уравнения: Tk(x) = cos(k arccos x) = 0. Получаем, что уравнение имеет k различных корней, расположенных на отрезке [-1,1]: которые и следует выбирать в качестве узлов интерполирования.

Нетрудно видеть, что корни на [-1,1] расположены симметрично и неравномерно — чем ближе к краям отрезка, тем корни расположены плотнее. Максимальное значение модуля полинома Чебышева равно 1 и достигается в точках

Если положить то для того, чтобы коэффициент при старшей степени полинома ωk(x) был равен 1,

Известно, что для любого полинома pk(x) степени k с коэффициентом, равным единице при старшей производной верно неравенство т.е. полиномы Чебышева являются полиномами, наименее уклоняющимися от нуля.

Вычислительный эксперимент

Для реализации поставленной задачи была написана программа на языке С++, которая по заданной функции приближает её каноническим полиномом. Разумеется, необходимо указать узлы, через которые полином пройдёт, и значения функции в этих узлах.

Далее строится СЛАУ, которая решается методом Гаусса. На выходе получаем коэффициенты для полинома и ошибку аппроксимации.

Как было показано выше, и в чём мы убедимся в дальнейшем, от выбора узлов зависит точность, с которой полином будет приближать функцию.

Пример: Интерполяция синуса

Попробуем интерполировать функцию y = sin(x) на отрезке [1, 8.5]. Выберем узлы интерполяции:

Полученный в результате интерполяции полином отображён на рисунке (синим цветом показан график y = sin(x), красным – интерполяционного полинома)

Ошибка интерполяции в этом случае: 0.1534

Давайте посмотрим, что произойдёт, если выбрать равномерно стоящие узлы для той же функции на том же отрезке.

На отрезке [3, 6] приближение, бесспорно, стало лучше. Однако разброс на краях очень большой. Ошибка интерполяции: 2.3466.

Наконец, выберем узлы интерполяции в соответствии с Чебышевским алгоритмом. Получим их по следующей формуле (просто сделаем замену переменной):

В нашем случае [a,b] — отрезок [1, 8.5], y = cosx, n+1 — количество узлов.

Остаётся открытым вопрос, какое количество узлов выбрать.

• При значении n меньше 3 ошибка аппроксимации получается более 10.6626.
• При n = 4: приближение лучше (ошибка равна 1.0111),
• при n = 5: ошибка аппроксимации 0.2797

График функций при n = 4 выглядит следующим образом:

При n = 7 ошибка аппроксимации принимает наименьшее из полученных ранее значений (для данного промежутка): 0.0181. График синуса (обозначен синим цветом) и аппроксимационного полинома (обозначен красным цветом) представлены на следующем графике:

Что интересно, если при этом же количестве узлов выбирать их на отрезке [1, 8], то ошибка аппроксимации становится ещё меньше : 0.0124. График в этом случае выглядит так:

При выборе большего количества узлов ситуация ухудшается: мы стараемся слишком точно приблизить исходную функцию:

Ошибка аппроксимации будет только расти с увеличением числа узлов.

Как видим, наилучшее приближение получается при выборе узлов по методу Чебышева. Однако рекомендаций, какое количество узлов является оптимальным, нет — это определяется только экспериментальным путём.

Рекомендации программисту

Программа написана на языке C++ с использованием библиотеки линейной алгебры UBlas, которая является частью собрания библиотек Boost. Скачать исходный текст программы можно здесь [2.55Кб].

Предварительные настойки

Чтобы воспользоваться программой, необходимо сделать следующее: 1. Определиться с функцией, которую вы собираетесь интерполировать 2. Создать текстовый файл (например, vec.txt), в первой строчке которого через пробел размещены узлы интерполяции, а во второй – значения выбранной функции в этих узлах.

Например, функция y = sin(x):

0.74 2 -3.5 0.6743 0.9093 0.351

3. В .cpp файле программы в функцию double f(double x) вместо строки return прописать возвращаемое исходной функцией значение. Например, для функции y = sin(x):

return sin(x);

4. В функции int main() исходного кода присвоить переменной char* flname путь к входному файлу с данными. В нашем случае char* flname = «vec.txt»;

Использование программы

В программе реализованы следующие основные функции:

• double f(double x), описание которой было дано выше
• int load(char *filename, vector y) — загрузка узлов интерполяции в переменную x и значения функции в этих узлах в переменную y текстового файла filename. В случае удачной загрузки данных из файла функция возвращает 0.
• void matrix2diag(matrix y) — приводит матрицу A к треугольному виду. y — столбец правой части (также изменяется вместе с матрицей A).
• void SolveSystem(matrix y, vector Лаборатория базовых знаний». Москва. 2003.
• И.С. Березин, Н.П. Жидков. Методы вычислений. Изд. ФизМатЛит. Москва. 1962.
• Дж. Форсайт, М.Мальком, К. Моулер. Машинные методы математических вычислений. Изд-во «Мир». Москва. 1980.

Смотри также

• Проблема выбора узлов для интерполяции
• Ошибки вычислений
• Метод наименьших квадратов
• Интерполяционный многочлен Лагранжа
• Практикум ММП ВМК, 4й курс, осень 2008

Ссылки

Источник: www.machinelearning.ru

Polinom — реальные отзывы о polinom.trade

Polinom – некая торговая платформа, которая представляет собой лучший инструмент для торговли на финансовых рынках. Очередное обещание халявы, не более.

Конечно же, никакой торговой платформы под названием Polinom не существует в природе. Ее просто придумали мошенники, чтобы иметь возможность с ее помощью разводить доверчивых посетителей на деньги. Поскольку здесь нет никакого маркетинга, отнести этот проект к классическим псевдоинвестиционным хайпам не получится. Это стопроцентное кидалово, лохотрон, который крайне неумело маскируется под некую трейдинговую компанию.

Как ищут проект

• Polinom отзывы
• Торговая платформа Полином

Сайт, конечно же, убогий. Он дешевый, и это видно. Зато есть два языка – русский и английский. Используется стандартный, недорогой шаблон. Есть вероятность, что админ вообще сюда ничего не вкладывал, а просто украл у кого-то идею.

Разве что на недорогой хостинг потратился, да и то, не факт, так как у него, скорее всего, он уже был оплачен, и это не первый его проект такого типа.

Юридическая информация, само собой, отсутствует. Это простительно для низкопробных псевдоинвестиционных проектов, а не для якобы супер перспективной торговой компании. Как она вообще может быть компанией, если на сайте polinom.trade нет ничего, что могло хотя бы косвенно это подтвердить?

Естественно, Polinom – это не более чем вымысел создателя. Никакая это не компания, нет здесь никаких лучших онлайн инструментов для прибыльной торговли на финансовых рынках. Есть только второсортный лохотрон, который собирает деньги с доверчивых лопухов, после чего предсказуемо их ворует. Как на такой примитив вообще можно вестись, понять сложно.

В качестве контактной информации нам предлагают указанный электронный ящик. И все! Есть поля «телефон» и «адрес», но они пустые. Это все, что вам надо знать о данной «компании». Надеяться на то, что тут будет полноценная связь с админом, конечно же, не нужно, потому что этого гарантированно не случится.

Да и зачем мошеннику что-то с вами обсуждать? Что он может сказать, что он кидала, и вы свои деньги больше никогда не увидите? Смешно.

Обзор и разоблачение
Итак, компания Polinom была создана, чтобы предложить нам некий лучший онлайн торговый инструмент. Здесь есть якобы интуитивная торговая платформа, разработанная по последним достижениям в области дигитальной торговли для профессиональных трейдеров. Polinom была создана как способ для трейдеров инвестировать в финансовые рынки на платформе, которая проста в использовании.

В целом, описание идеально подходит для второсортного хайпика, который протянет максимум неделю, но никак не для якобы крупной трейдинговой компании. Так что админ, у которого нет ни средств, ни опыта для создания высококачественных пирамидальных структур, явно не сумел сделать хоть что-то, чтобы привлекало внимание потенциальных вкладчиков. Потому что Polinom – это дно.

Как уже было сказано выше, никаких инвестиционных планов здесь нет. Нам нужно пройти несложную регистрацию, после чего мошенник начнет нам рассказывать, что и как надо делать. Хотя это и так понятно – конечно же, вкладывать свои деньги, которые якобы где-то там будут торговаться. Но в реальности эти средства будут моментально украдены, и взамен вы ничего не получите, ни копейки.

Вердикт
Polinom – это мошенничество. Дешевый лохотрон, который неумело пытается выставить себя крупной и перспективной компанией. Ни в коем случае не связывайтесь, это развод на деньги.

Среди всего разнообразия лохотронов, у нас есть качественные и рабочие проекты.
На сайте есть рубрика: Проверенный заработок!
Это рабочий способ заработка — он помогает заработать реальные деньги!

Анатолий Дмитриев / автор обзора

Один из лучших экспертов в сфере безопасности, финансовый аналитик со стажем! Опыт работы более 5 лет! Любит свою работу.

Похожие обзоры

3 комментария к “Polinom — реальные отзывы о polinom.trade”

И я так же попалась! Только они уже более года долбят меня, так как я номер телефона не сменила)))хорошо,что банк второй платеж заблокировал. Ответить

Что делать если уже повелся Ответить

Хочу предупредить всех о полином трейд , это мошеннический сайт предлагают установить типа партнёрскую программу , на самом деле это программа удалённого доступа и выводят средства с карт. Возврата не добьешься , потом позвонили сказали переведут деньги обратно но попытались снять ещё, хорошо что банк заблокировал карты , и сразу пропали прошёл верификации и опять пропали через три месяца они снимают 50 евро за бездействия но вывод не дают молчат так что это лохотрон запомните ПОЛИНОМ ТРЕЙД обходить сТоронто мошенники. Ответить

Оставьте комментарий Отменить ответ

Поиск

Свежие обзоры

• Ticketscloud — отзывы клиентов, возврат билетов
• Отзывы о ml-appvip.com — развод?
• NPB Invest отзывы — проект от брокера NPBFX
• Отзывы клиентов о Simebit — что это?
• Лохотрон Metaversesworld — отзывы клиентов

Последние проверки

Свежие комментарии

• Алексей Малышев к записи Отзывы и обзор melcocrownfb.com — что за сайт?
• олег к записи Отзывы и обзор melcocrownfb.com — что за сайт?
• николай к записи Hermes Management Ltd — реальные отзывы клиентов о гермес менеджмент
• Rover к записи S-Group отзывы — инвестиционная компания s-group.io
• светлана к записи WOWketo24 — как отписаться и отзывы о Wowketo24.com

• Ставки на спорт
• Инвестиционные проекты
• Обменники
• Опасная медицина
• Разное

• Пользовательское соглашение
• Политика конфиденциальности
• Отказ от ответственности

Этот сайт использует cookie для хранения данных. Продолжая использовать сайт, Вы даете свое согласие на работу с этими файлами. OK

Источник: seoseed.ru

Деление полинома на полином

Добрый вечер! Это программа, которая будет делить полином на полином, но она не совсем правильно работает, а я не могу сообразить, как её исправить. Подскажите, пожалуйста, как её исправить?

В классе два конструктора:

Polynom::Polynom(void) < n = 0; a = new float [n+1]; for(int i=1; iPolynom::Polynom(int N)< if (N>=0) < n = N; a = new float [n+1]; for(int i=1; i>
Polynom Polynom::operator/(Polynom t) < //сюда задается полином, который делит исходный if(t.n==0)< //делит на число (полином нулевой степени), работает правильно Polynom c(n); for(int i = 0; ireturn c; > else < //делит на полином, правильно выводит только последний элемент. if (n>=t.n)< int k = n-t.n; Polynom c(k); //создается новый полином, который и должен быть ответом for (int i = k; i>=t.n; i = k-t.n) < c.a[i] = a[n]/t.a[t.n]; Polynom h = c*t; Polynom r = ReadFile(«data1.txt»); //тут из файла считывается исходный полином, который мы делим. (к его полям выше обращались через n и a[i]) Polynom f = r — h; >return c; > > >

P.S. все операторы сложения, вычитания и умножения полиномов уже написаны в программе и работают правильно.

Попробуй разобраться с этим.

Описание класса и конструкторы-деструкторы:

class Polynom < private: int degree; double *coef; Polynom(int adegree); void reduce(void); friend Polynom plus_minus (const Polynom p2, double op(double, double)); public: Polynom(int adegree, double acoef[]); Polynom(const Polynom ~Polynom(); string to_s(void) const; friend Polynom operator + (const Polynom p2); friend Polynom operator — (const Polynom p2); friend Polynom operator * (const Polynom p2); friend Polynom operator / (const Polynom p2); friend ostream (istream p); >; Polynom::Polynom(int adegree) < degree = adegree; coef = new double[degree]; for (int i = 0; i < degree; i++) < coef[i] = 0.0; >> Polynom::Polynom(int adegree, double acoef[]) < degree = adegree; coef = new double[degree]; for (int i = 0; i < degree; i++) < coef[i] = acoef[i]; >> Polynom::Polynom(const Polynom degree = p.degree; coef = new double[degree]; for (int i = 0; i < degree; i++) < coef[i] = p.coef[i]; >> Polynom::~Polynom() < delete [] coef; >void Polynom::reduce(void) < int tdeg = degree; for (int i = degree — 1; i >= 0; i—) < if (coef[i] != 0.0) break; else tdeg—; >degree = tdeg; >

А вот функция деления:

Polynom operator / (const Polynom p2) < Polynom temp = p1; int rdeg = temp.degree — p2.degree + 1; Polynom res(rdeg); for (int i = 0; i < rdeg; i++) < res.coef[rdeg — i — 1] = temp.coef[temp.degree — i — 1] / p2.coef[p2.degree — 1]; for (int j = 0; j < p2.degree; j++) < temp.coef[temp.degree — j — i — 1] -= p2.coef[p2.degree — j — 1] * res.coef[rdeg — i — 1]; >> temp.reduce(); if (temp.degree != 0) < cout return res; >

Если интересно, могу скинуть программку целиком. Она, правда, достаточно длинная ))

Оно того стоило?

Можешь мне скинуть программу целиком пожайлуста?

// Polynom.cpp: определяет точку входа для консольного приложения. // #include «stdafx.h» #include #include using namespace std; double plus(double a, double b) < return a + b; >double minus(double a, double b) < return a — b; >class Polynom < private: int degree; double *coef; Polynom(int adegree); void reduce(void); friend Polynom plus_minus (const Polynom p2, double op(double, double)); public: Polynom(int adegree, double acoef[]); Polynom(const Polynom ~Polynom(); string to_s(void) const; friend Polynom operator + (const Polynom p2); friend Polynom operator — (const Polynom p2); friend Polynom operator * (const Polynom p2); friend Polynom operator / (const Polynom p2); friend ostream (istream p); >; Polynom::Polynom(int adegree) < degree = adegree; coef = new double[degree]; for (int i = 0; i < degree; i++) < coef[i] = 0.0; >> Polynom::Polynom(int adegree, double acoef[]) < degree = adegree; coef = new double[degree]; for (int i = 0; i < degree; i++) < coef[i] = acoef[i]; >> Polynom::Polynom(const Polynom degree = p.degree; coef = new double[degree]; for (int i = 0; i < degree; i++) < coef[i] = p.coef[i]; >> Polynom::~Polynom() < delete [] coef; >string Polynom::to_s(void) const < string str = «»; str += «[ degree = » + to_string(degree) + » :»; for (int i = degree — 1; i >= 0; i—) < str += » » + to_string(coef[i]); >str += » ]»; return str; > void Polynom::reduce(void) < int tdeg = degree; for (int i = degree — 1; i >= 0; i—) < if (coef[i] != 0.0) break; else tdeg—; >degree = tdeg; > Polynom plus_minus (const Polynom p2, double op(double, double)) < Polynom *pmax, *pmin; if (p1.degree >p2.degree) < pmax = (Polynom *)&p1; pmin = (Polynom *)&p2; >else < pmax = (Polynom *)&p2; pmin = (Polynom *)&p1; >int min_degree = pmin->degree ; int max_degree = pmax->degree; Polynom res(max_degree); for (int i = 0; i < max_degree; i++) if (i < min_degree) < res.coef[i] = op(pmax->coef[i], pmin->coef[i]); > else < res.coef[i] = pmax->coef[i]; > return res; > Polynom operator + (const Polynom p2) < return plus_minus(p1, p2, plus); >Polynom operator — (const Polynom p2) < return plus_minus(p1, p2, minus); >Polynom operator * (const Polynom p2) < Polynom res(p1.degree + p2.degree — 1); for (int i = 0; i < p1.degree; i++) < for (int j = 0; j < p2.degree; j++) < res.coef[i+j] += p1.coef[i] * p2.coef[j]; >> return res; > Polynom operator / (const Polynom p2) < Polynom temp = p1; int rdeg = temp.degree — p2.degree + 1; Polynom res(rdeg); for (int i = 0; i < rdeg; i++) < res.coef[rdeg — i — 1] = temp.coef[temp.degree — i — 1] / p2.coef[p2.degree — 1]; for (int j = 0; j < p2.degree; j++) < temp.coef[temp.degree — j — i — 1] -= p2.coef[p2.degree — j — 1] * res.coef[rdeg — i — 1]; >> temp.reduce(); if (temp.degree != 0) < cout return res; > ostream operator >> (istream p) < int ndeg = 0; stream >> ndeg; if (ndeg != p.degree) < delete [] p.coef; p.degree = ndeg; p.coef = new double[ndeg]; for (int i = 0; i < ndeg; i++) p.coef[i] = 0.0; >for (int i = 0; i < ndeg; i++) stream >> p.coef[i]; return stream; > int _tmain(int argc, _TCHAR* argv[]) < setlocale(LC_CTYPE, «Russian»); double c1[] = < 1.0, 2.0, 3.0 >; double c2[] = < 5.0, 6.0 >; double c3[] = < 5.0, 2.0 >; Polynom p1(3, c1), p2(2, c2); cout

деление работает неверно

Анита, а что-то из конкретных примеров можно увидеть?

Внимание! Это довольно старый топик, посты в него не попадут в новые, и их никто не увидит. Пишите пост, если хотите просто дополнить топик, а чтобы задать новый вопрос — начните новый.

Источник: code-live.ru