Программа поиска максимума функции

Содержание

Пусть дан массив A длины N, и дано число K ≤ N. Требуется найти максимум (минимум, сумма . ) в подотрезках длины K данного массива. Это частный случай задачи RMQ (Range Minimum Query — минимум на отрезке), но с дополнительными ограничениями — постоянная длина отрезка поиска. В данном решении задача не предполагает возможность изменения элементов массива. Для определенности будем рассматривать нахождение максимума.

Преимущества и недостатки

Алгоритм нахождения максимума функции

Простейшая задача нахождения максимума функции решается по следующему алгоритму:

Задаются границы a и b, в пределах которых имеется максимум функции.
Интервал [a,b] разбивается на определенное количество шагов.
Функция табулируется в пределах заданного интервала, и каждое вычисленное значение функции сравнивается с максимальным (заданным до начала табулирования).
Находится максимальное значение функции на заданном интервале с определенным шагом и выводится на печать.

Блок-схема алгоритма имеет вид:

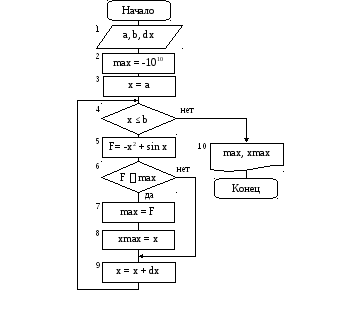
Индуктивные функции на Си: поиск максимума

Рис. 4. Блок – схема алгоритма нахождения максимума функции Естественно, что с уменьшением шага изменения аргумента точность вычисления максимума увеличивается.

Можно воспользоваться и следующим алгоритмом:

Найти значение максимума по алгоритму, представленному выше.
Для дальнейшего рассмотрения выбрать отрезок [xmax-dx, xmax+dx] и выполнить вычисление максимума с шагом, например, dx/10.
Сравнить два найденных значения.

Блок – схема решения задачи имеет вид:

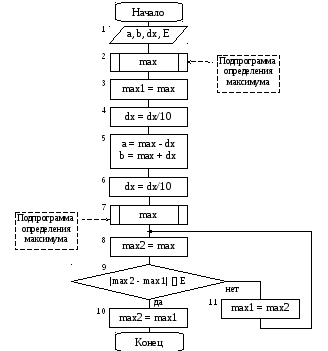
Рис. 5. Блок – схема алгоритма нахождения максимума функции

Методы оптимизации функций одной переменной Метод равномерного поиска

Этот метод основан на том, что переменной x присваиваются значения x+∆x с шагом ∆x = const и вычисляются значения F(x). Если F(x n+1)>F(xn), переменной x даётся новое приращение. Как только F(xn+1)станет меньше F(x) поиск останавливается. При малой заданной погрешности этот метод неэкономичен по затратам машинного времени.

Метод поразрядного приближения

Задаём начальное приближение x=x₀ слева от максимума F(x) и вычисляем F(x₀). Задаём D=h, где h=∆x – начальный шаг поиска.
Полагаем, что G=F(xn), где вначале F(xn)=F(x₀), задаём x=x+D и вычисляем F(x n+1)=F(x).
Проверяем условие F(x n₊₁)>G; если оно выполняется, идём к п.2, если нет, то к п.4.
Полагаем D=-D/4. Проверяем условие |D|>E/4, где E – заданная погрешность вычисления xn в точке максимума. Если оно выполняется, идём к п.2, т.е. обеспечиваем поиск максимума в другом направлении с шагом в 4 раза меньше прежнего. Если данное условие выполняется, процесс вычисления заканчиваем.

Метод дихотомии

Проверяем условие |b-a|n. Если это условие выполняется, идём к п.6; если не выполняется, идём к п.2.
Делим интервал поиска [a, b] пополам и вычисляем две абсциссы, симметрично расположенные относительно точки

Для этих значений x вычисляем F(x₁)>F(x₂).
Проверяем условие F(x₁)>F(x₂). Если оно выполняется, полагаем b=x₂ и идём к п.1. Если не выполняется, идём к п.5.
Полагаем a=x₁ и идём к п.1.
Выводим на печать xn=(a+b)/2 и вычисляем F(xn).

Источник: studfile.net

АЛГЕБРА С НУЛЯ — Точки Экстремума Функции