Программа описательная статистика что это

Описательные статистики

Пусть Х1, Х2 . Xn — выборка независимых случайных величин.

Упорядочим эти величины по возрастанию, иными словами, построим вариационный ряд:

Элементы вариационного ряда (*) называются порядковыми статистиками.

Величины d(i) = X(i+1) — X(i) называются спейсингами или расстояниями между порядковыми статистиками.

Размахом выборки называется величина

Иными словами, размах это расстояние между максимальным и минимальным членом вариационного ряда.

Выборочное среднее равно: = (Х1 + Х2 + . + Xn) / n

Среднее арифметическое

Вероятно, большинство из вас использовало такую важную описательную статистику, как среднее.

Среднее — очень информативная мера «центрального положения» наблюдаемой переменной, особенно если сообщается ее доверительный интервал. Исследователю нужны такие статистики, которые позволяют сделать вывод относительно популяции в целом. Одной из таких статистик является среднее.

ОПИСАТЕЛЬНАЯ статистика | АНАЛИЗ ДАННЫХ #3

Доверительный интервал для среднего представляет интервал значений вокруг оценки, где с данным уровнем доверия, находится «истинное» (неизвестное) среднее популяции.

Например, если среднее выборки равно 23, а нижняя и верхняя границы доверительного интервала с уровнем p=.95 равны 19 и 27 соответственно, то можно заключить, что с вероятностью 95% интервал с границами 19 и 27 накрывает среднее популяции.

Если вы установите больший уровень доверия, то интервал станет шире, поэтому возрастает вероятность, с которой он «накрывает» неизвестное среднее популяции, и наоборот.

Хорошо известно, например, что чем «неопределенней» прогноз погоды (т.е. шире доверительный интервал), тем вероятнее он будет верным. Заметим, что ширина доверительного интервала зависит от объема или размера выборки, а также от разброса (изменчивости) данных. Увеличение размера выборки делает оценку среднего более надежной. Увеличение разброса наблюдаемых значений уменьшает надежность оценки.

Вычисление доверительных интервалов основывается на предположении нормальности наблюдаемых величин. Если это предположение не выполнено, то оценка может оказаться плохой, особенно для малых выборок.

При увеличении объема выборки, скажем, до 100 или более, качество оценки улучшается и без предположения нормальности выборки.

Довольно трудно «ощутить» числовые измерения, пока данные не будут содержательно обобщены. Диаграмма часто полезна в качестве отправной точки. Мы можем также сжать информацию, используя важные характеристики данных. В частности, если бы мы знали, из чего состоит представленная величина, или если бы мы знали, насколько широко рассеяны наблюдения, то мы бы смогли сформировать образ этих данных.

Среднее арифметическое, которое очень часто называют просто «среднее», получают путем сложения всех значений и деления этой суммы на число значений в наборе.

Описательная статистика (часть 1): ключевые определения за 15 минут.

Это можно показать с помощью алгебраической формулы. Набор n наблюдений переменной X можно изобразить как X1, X2, X3, . Xn. Например, за X можно обозначить рост индивидуума (см), X1 обозначит рост 1-го индивидуума, а Xi — рост i-го индивидуума. Формула для определения среднего арифметического наблюдений (произносится «икс с чертой»):

Можно сократить это выражение:

где (греческая буква «сигма») означает «суммирование», а индексы внизу и вверху этой буквы означают, что суммирование производится от i = 1 до i = n. Это выражение часто сокращают еще больше:

или

Медиана

Если упорядочить данные по величине, начиная с самой маленькой величины и заканчивая самой большой, то медиана также будет характеристикой усреднения в упорядоченном наборе данных.

Медиана делит ряд упорядоченных значений пополам с равным числом этих значений как выше, так и ниже ее (левее и правее медианы на числовой оси).

Вычислить медиану легко, если число наблюдений n нечетное. Это будет наблюдение номер (n + 1)/2 в нашем упорядоченном наборе данных.

Например, если n = 11, то медиана — это (11 + 1)/2, т. е. 6-е наблюдение в упорядоченном наборе данных.

Если n четное, то, строго говоря, медианы нет. Однако обычно мы вычисляем ее как среднее арифметическое двух соседних средних наблюдений в упорядоченном наборе данных (т. е. наблюдений номер (n/2) и (n/2 + 1)).

Так, например, если n = 20, то медиана — это среднее арифметическое наблюдений номер 20/2 = 10 и (20/2 + 1) = 11 в упорядоченном наборе данных.

Мода

Мода — это значение, которое встречается наиболее часто в наборе данных; если данные непрерывные, то мы обычно группируем их и вычисляем модальную группу.

Некоторые наборы данных не имеют моды, потому что каждое значение встречается только 1 раз. Иногда бывает более одной моды; это происходит тогда, когда 2 значения или больше встречаются одинаковое число раз и встречаемость каждого из этих значений больше, чем любого другого значения.

Как обобщающую характеристику моду используют редко.

Среднее геометрическое

При несимметричном распределении данных сред­нее арифметическое не будет обобщающим показа­телем распределения.

Если данные скошены вправо, то можно создать более симметричное распределе­ние, если взять логарифм (по основанию 10 или по основанию е) каждого значения переменной в наборе данных. Среднее арифметическое значений этих логарифмов — характеристика распределения для преобразованных данных.

Чтобы получить ме­ру с теми же единицами измерения, что и первона­чальные наблюдения, нужно осуществить обратное преобразование — потенцирование (т. е. взять анти­логарифм) средней логарифмированных данных; мы называем такую величину среднее геометрическое.

Если распределение данных логарифма приблизитель­но симметричное, то среднее геометрическое подобно медиане и меньше, чем среднее необработанных дан­ных.

Взвешенное среднее

Взвешенное среднее используют тогда, когда не­которые значения интересующей нас переменной x более важны, чем другие. Мы присоединяем вес wi к каждому из значений xi в нашей выборке для то­го, чтобы учесть эту важность.

Если значения x1, x2 . xn имеют соответствующий вес w1, w2 . wn, то взвешенное арифметическое среднее выглядит следующим образом:

Например, предположим, что мы заинтересованы в определении средней продолжительности госпита­лизации в каком-либо районе и знаем средний реа­билитационный период больных в каждой больнице. Учитываем количество информации, в первом при­ближении принимая за вес каждого наблюдения число больных в больнице.

Взвешенное среднее и среднее арифметическое идентичны, если каждый вес равен единице.

Размах (интервал изменения)

Размах — это разность между максимальным и минимальным значениями переменной в наборе данных; этими двумя величинами обозначают их разность. Обратите внимание, что размах вводит в заблуждение, если одно из значений есть выброс (см. раздел 3).

Размах, полученный из процентилей

Что такое процентили

Предположим, что мы расположим наши данные упорядоченно от самой маленькой величины перемен­ной X и до самой большой величины. Величина X, до которой расположен 1% наблюдений (и выше которой расположены 99% наблюдений), называется первым процентилем.

Величина X, до которой находится 2% наблюдений, называется 2-м процентилем, и т. д.

Величины X, которые делят упорядоченный набор значений на 10 равных групп, т. е. 10-й, 20-й, 30-й. 90 и процентили, называются децилями. Величины X, которые делят упорядоченный набор значений на 4 равные группы, т.е. 25-й, 50-й и 75-й процентили, называются квартилями. 50-й процентиль — это ме­диана .

Применение процентилей

Мы можем добиться такой формы описания рас­сеяния, на которую не повлияет выброс (аномальное значение), исключая экстремальные величины и определяя размах остающихся наблюдений.

Межквартильный размах — это разница между 1-м и 3-м квартилями, т.е. между 25-м и 75-м процентилями. В него входят центральные 50% наблюдений в упорядоченном наборе, где 25% наблюдений находятся ниже центральной точки и 25% — выше.

Интердецильный размах содержит в себе центральные 80% наблюдений, т. е. те наблю­дения, которые располагаются между 10-м и 90-м процентилями.

Мы часто используем размах, который содержит 95% наблюдений, т.е. он исключает 2,5% наблюдений снизу и 2,5% сверху. Указание такого интервала актуально, например, для осуществления диагностики болезни. Такой интервал называется референтный интервал, референтный размах или нормальный размах.

Дисперсия

Один из способов измерения рассеяния данных за­ключается в том, чтобы определить степень отклоне­ния каждого наблюдения от средней арифметической. Очевидно, что чем больше отклонение, тем больше изменчивость, вариабельность наблюдений.

Однако мы не можем использовать среднее этих отклонений как меру рассеяния, потому что положительные от­клонения компенсируют отрицательные отклонения (их сумма равна нулю). Чтобы решить эту проблему, мы возводим в квадрат каждое отклонение и находим среднее возведенных в квадрат отклонений; эта величина называется вариацией, или дисперсией.

Возьмем n наблюдений x1, x2 , х3, . xn , среднее которых равняется .

В случае, если мы имеем дело не с генеральной совокупностью, а с выборкой, то вычисляется выборочная дисперсия:

Теоретически можно показать, что полу­чится более точная дисперсия по выборке, если разделить не на n, а на (n-1).

Единицы измерения (размерность) вариации — это квадрат единиц измерения первоначальных на­блюдений.

Например, если измерения производятся в килограммах, то единица измерения вариации будет килограмм в квадрате.

Среднеквадратическое отклонение, стандартное отклонение выборки

Среднеквадратическое отклоне­ние — это положительный квадратный корень из дисперсии.

Стандартное отклонение выборки — корень из выборочной дисперсии:

Мы можем представить себе стандартное отклоне­ние как своего рода среднее отклонение наблюдений от среднего. Оно вычисляется в тех же единицах (размерностях), что и исходные данные.

Если разделить стандартное отклонение на сред­нее арифметическое и выразить результат в процен­тах, получится коэффициент вариации.

Он являет­ся мерой рассеяния, не зависит от единиц измерения (безразмерный), но имеет некоторые теоретические не­удобства и поэтому не очень одобряется статистиками.

Вариация в пределах субъектов и между субъектами

Если провести повторные измерения непрерывной переменной у исследуемого объекта, то можно увидеть ее изме­нения (внутрисубъектные изменения). Это можно объяснить тем, что объект не всегда может дать точные и те же самые ответы, и/или ошибкой, погрешностью измерения. Однако при измерениях у одного объекта вариация обычно меньше, чем вариация единичного измерения в группе (межсубъектные изменения).

Например, вместимость легкого 17-летнего мальчика составляет от 3,60 до 3,87 л, когда измерения повторяются не менее 10 раз; если провести однократное измерение у 10 мальчиков того же возраста, то объем будет между 2,98 и 4,33 л. Эти концепции важны в плане исследования.

Источник: statistica.ru

Применение описательной статистики в Microsoft Excel

Пользователи Эксель знают, что данная программа имеет очень широкий набор статистических функций, по уровню которых она вполне может потягаться со специализированными приложениями. Но кроме того, у Excel имеется инструмент, с помощью которого производится обработка данных по целому ряду основных статистических показателей буквально в один клик.

Этот инструмент называется «Описательная статистика». С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Давайте взглянем, как работает данный инструмент, и остановимся на некоторых нюансах работы с ним.

Использование описательной статистики

Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.

В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:

• Медиана;
• Мода;
• Дисперсия;
• Среднее;
• Стандартное отклонение;
• Стандартная ошибка;
• Асимметричность и др.

Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.

Подключение «Пакета анализа»

Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.

1. Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
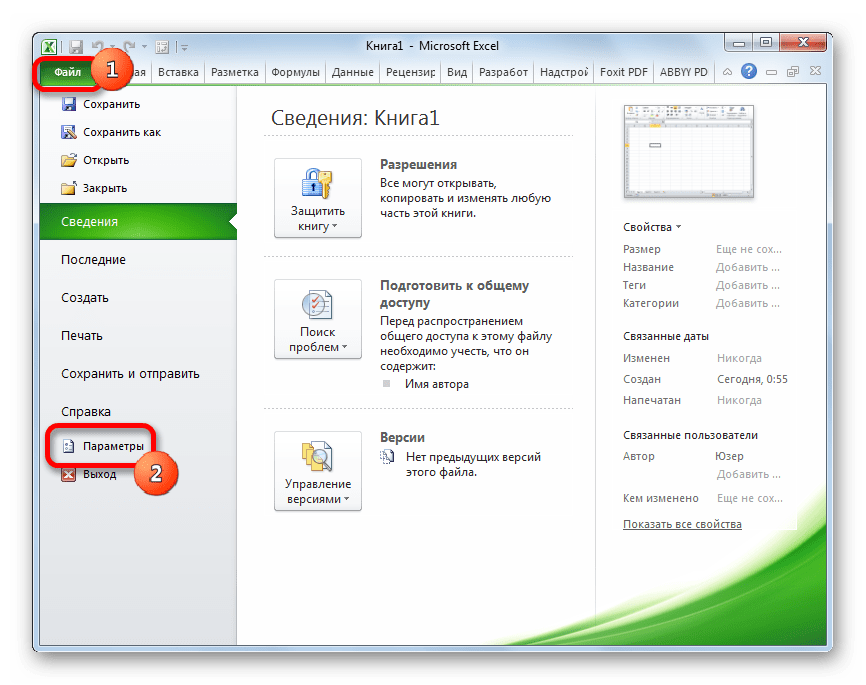
2. В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
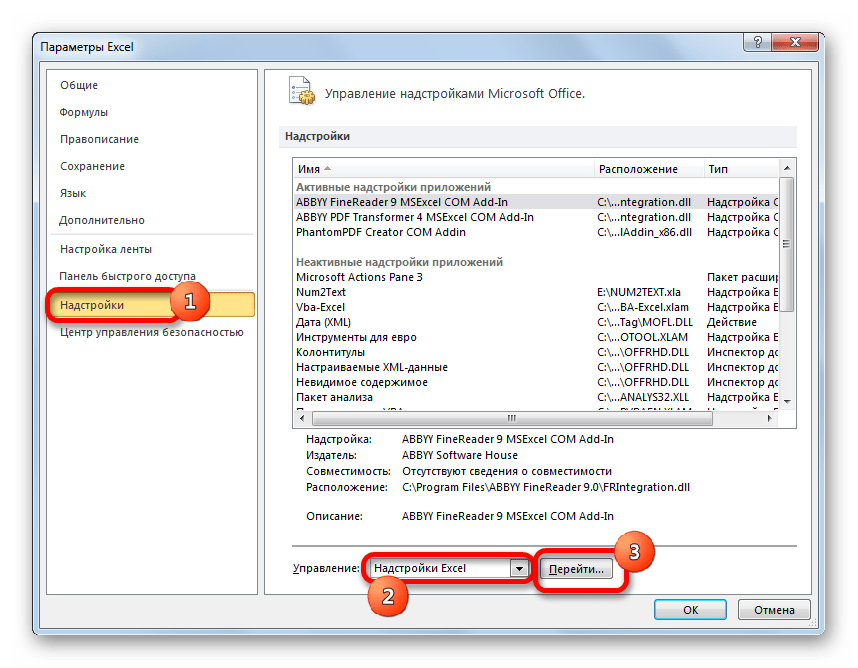
3. Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.

Применение инструмента «Описательная статистика»

Теперь посмотрим, как инструмент описательная статистика можно применить на практике. Для этих целей используем готовую таблицу.

1. Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ».
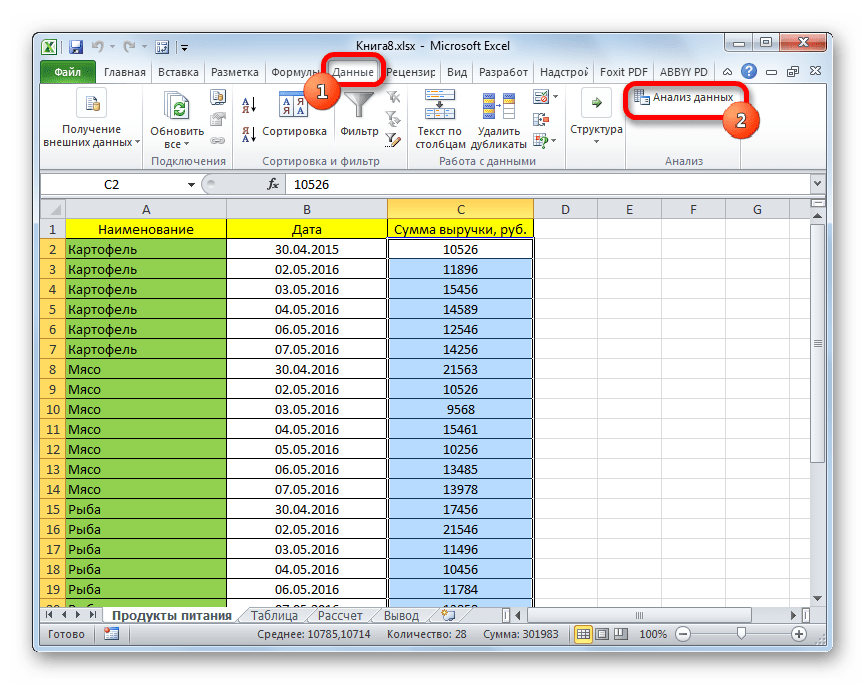
2. Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK».
3. После выполнения данных действий непосредственно запускается окно «Описательная статистика». В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Для того, чтобы внести нужные нам координаты, устанавливаем курсор в указанное поле. Затем, зажав левую кнопку мыши, выделяем на листе соответствующую табличную область. Как видим, её координаты тут же отобразятся в поле. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.

• Выходной интервал;
• Новый рабочий лист;
• Новая рабочая книга.

В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на новом рабочем листе под названием «Итоги».

Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.

Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Но в нашем случае этот параметр так же, как и предыдущий, не является обязательным, поэтому флажки мы не ставим.

После того, как все указанные данные внесены, жмем на кнопку «OK».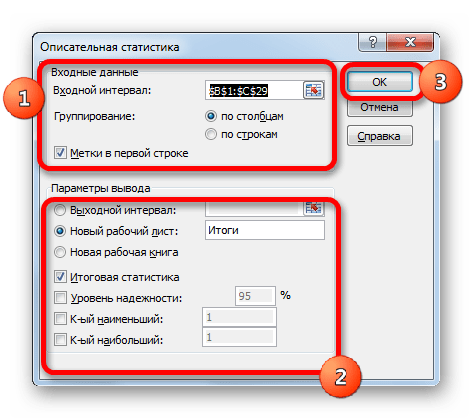

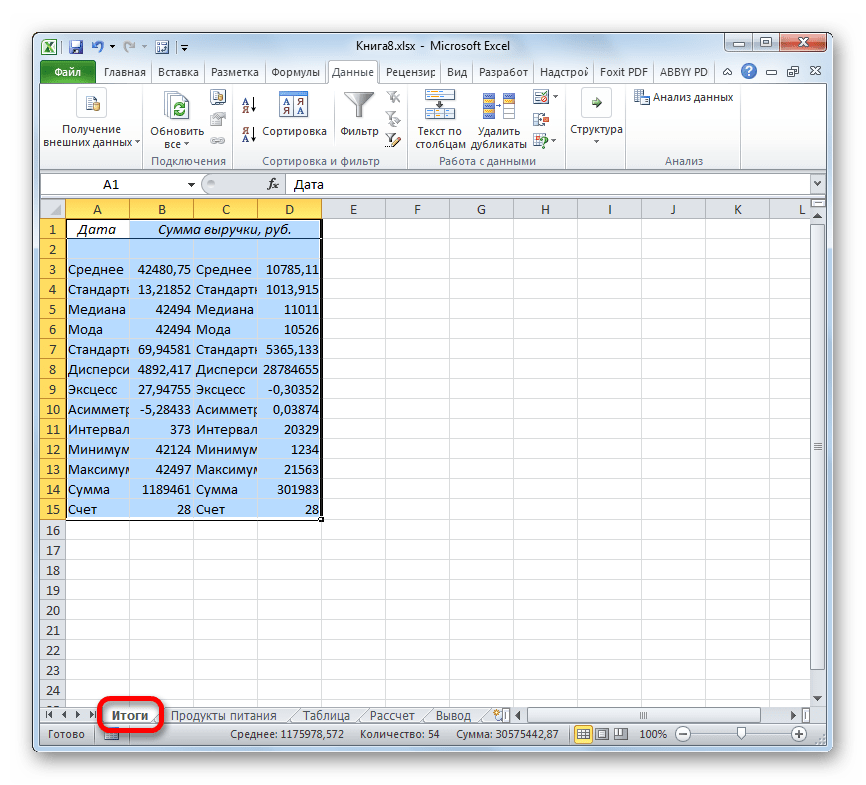
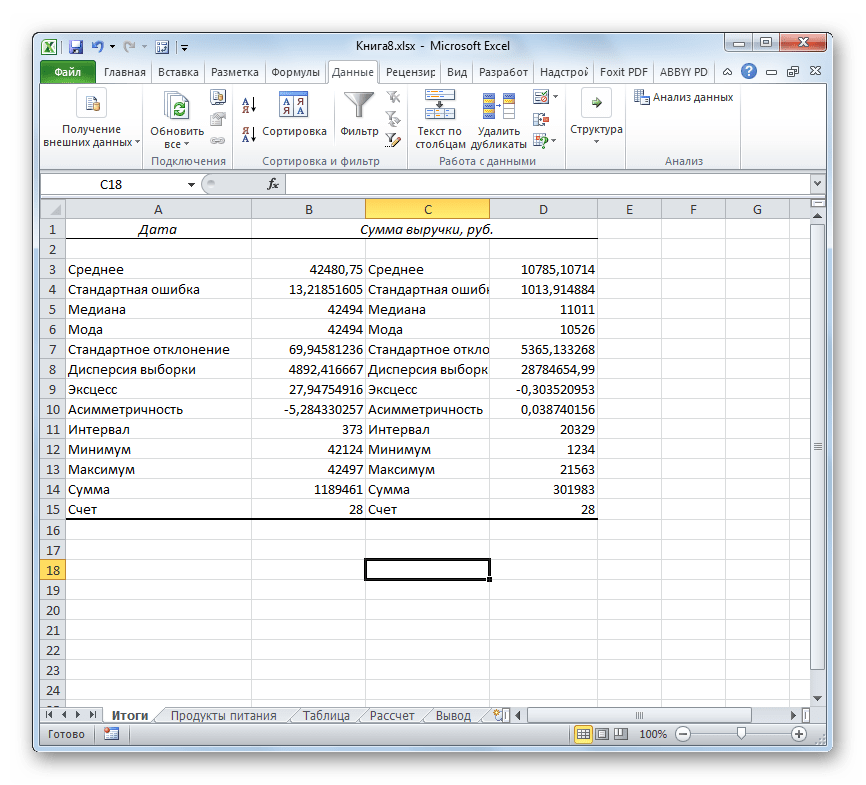
После выполнения этих действий таблица с описательной статистикой выводится на отдельном листе, который был нами назван «Итоги». Как видим, данные представлены сумбурно, поэтому их следует отредактировать, расширив соответствующие колонки для более удобного просмотра.

После того, как данные «причесаны» можно приступать к их непосредственному анализу. Как видим, при помощи инструмента описательной статистики были рассчитаны следующие показатели:

Асимметричность;

Интервал;

Минимум;

Стандартное отклонение;

Дисперсия выборки;

Максимум;

Сумма;

Эксцесс;

Среднее;

Стандартная ошибка;

Медиана;

Мода;

Счет.

Если какие-то из вышеуказанных данных для конкретного вида анализа не нужны, то их можно удалить, чтобы они не мешали. Далее производится анализ с учетом статистических закономерностей.

Как видим, с помощью инструмента «Описательная статистика» можно сразу получить результат по целому ряду критериев, которые в ином случае рассчитывались с применением отдельно предназначенной для каждого расчета функцией, что заняло бы значительное время у пользователя. А так, все эти расчеты можно получить практически в один клик, использовав соответствующий инструмент — Пакета анализа.

Мы рады, что смогли помочь Вам в решении проблемы.

Источник: lumpics.ru

Описательная статистика в SPSS

В SPSS в «описательную статистику» входит 4 значимых раздела: 1) подсчет частотных характеристик данных, 2) вычисление собственно описательных статистик, 3) расчет разведывательных статистик, 4) построение таблиц сопряженности (рис. 12). Внутренний функционал этих разделов очень похож и в целом позволяет считать одно и то же. Обычно выбирают одну из предложенных форм расчета.

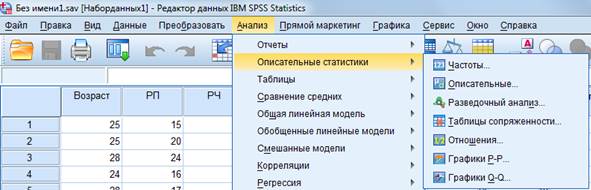
Рисунок 12 – Функционал раздела «Описательная статистика» IBM SPSS Statistics

Рассмотрим некоторые из них подробнее.

1) Анализ (Analyze) → Описательные статистики → Частоты.Подсчет частотных характеристик. Диалоговое окно: два просмотровых окна, мышкой переправляются нужные поля слева направо. Мы уже рассматривали работу данного меню в рамках построения частотных таблиц. Однако кроме описанных выше возможностей этот раздел позволяет рассчитывать описательную статистику.

Для этого используются первые две кнопки, расположенные справа в диалоговом окне «Частоты» (рис. 8).

Кнопка «Статистика» содержит следующие разделы (рис. 13):

1) значения процентелей (percentile values) – «четверти» (quartiles – квартили), «процентили для … равных групп» (cut point for … equal groups – можно вычислить процентные оценки, разбив выборку на группы (от 2 до 100), равные по количеству респондентов), «процентили … добавить» (percentiles … add – можно запросить вычисление нескольких произвольных процентных значений, например, 15 %, 30 % и т. д.);

2) разброс (меры рассеяния) – «стандартное отклонение» (std. deviation), «дисперсия» (variance), «размах» (rang), «минимум» (minimum), «максимум» (maximum), «стандартная ошибка среднего» (S.E. mean);

3) расположение (central tendency – меры центральной тенденции) – «среднее» (mean – среднее арифметическое), «медиана», «мода», «сумма»;

4) распределение – «асимметрия», «эксцесс».

Выбор описательных статистик осуществляет проставлением галочек для соответствующих из них →добавить →ok. Появляется окно «Вывод», в котором содержаться таблицы со статистиками для выбранных переменных (рис. 13).

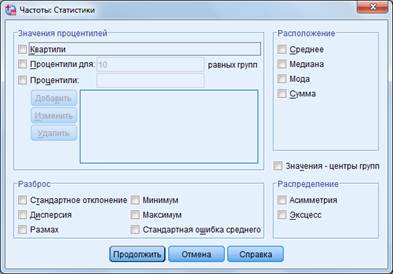
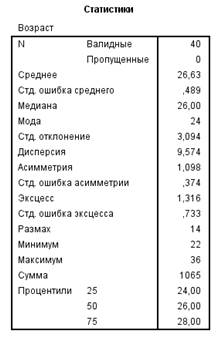
Рисунок 13 – Функционал раздела «Частотные статистики» и таблица расчета статистик

Кнопка «Диаграммы» содержит разделы: «столбиковые» (bar charts), «круговые» (pie charts), «гистограмма» и «показать нормальную кривую» (histograms 2) «сумма»; 3) разброс (меры рассеяния) – «стандартное отклонение» (std. deviation), «дисперсия» (variance), «размах» (rang), «минимум» (minimum), «максимум» (maximum), «стандартная ошибка среднего» (S.E. mean); 4) распределение — «эксцесс» и «ассиметрия»; 5) порядок вывода (рис. 15).

Рисунок 15 – Функционал раздела «Описательные статистики: Параметры»

3) Анализ (Analyze) → Описательные статистики → Разведочный анализ позволяет исследовать любое количество переменных (рис. 16). При этом выводятся и таблицы сопряженности, и графики, и описательная статистика (для этого используются находящиеся справа кнопки «Статистика» и «Графики»).

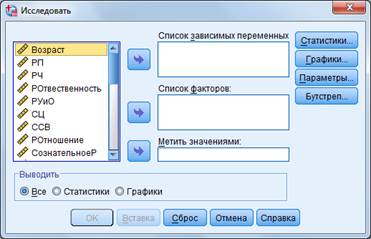
Рисунок 16 – Функционал раздела «Разведочный анализ»

4) Анализ (Analyze) → Описательные статистики → Таблицы сопряженности позволяет строить таблицы сопряженности. Таблицы сопряженности позволяют получить наглядное изображение (в виде частотной таблицы) совместного распределения двух переменных (например, пола респондентов и возраста начала курения), а также проверить гипотезу о наличии связи между ними. Порядок работы: выбор поля, показатели по которому должны содержаться в строках (например, пол) → переправка ( ) в графу «строки» (row(s) – в результатах эти данные будут располагаться в боковой графе таблицы), для второго поля – переправка в графу «столбцы» (column(s) – в результатах значения окажутся в шапке таблицы) (рис. 17).

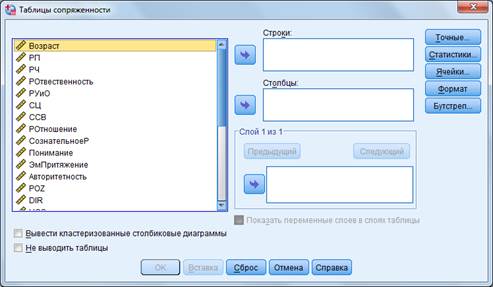
Рисунок 17 – Диалоговое окно «Таблицы сопряженности» IBM SPSS Statistics

Кнопка «Статистики» содержит следующие математические критерии (рис. 18):

1) хи-квадрат (Chi-square) – для номинальных, в том числе дихотомических, шкал;

2) корреляция (correlation) считается по-разному: для ранговых шкал – коэффициент ранговой корреляции Спирмена, для интервальных – коэффициент линейной корреляции Пирсона;

3) раздел «Nominal» – только для номинативной шкалы: а) «коэффициент сопряженности» (contingency coefficient), б) «Фи и Ви Крамера» (Phi and Cramer’s V – Фи-критерий и V-критерий Крамера), в) «лямбда» (Lambda – критерий лямбда Гудмена-Крускела), г) «коэф. колебания» (Uncertainly coefficient – коэффициент неопределенности);

4) раздел «порядковая» (ordinal) – только для порядковой шкалы: а) «гамма» (Gamma – критерий гамма Гудмена-Краскела), б) «Сомерс» (Somers’ d – критерий D Соммерса), в) «Кэндаль Тау-б» (Kendall’s tau-b – тау-б критерий Кендалла), г) «Кэндаль Тау-ц» (Kendall’s tau-с – тау-це критерий Кендалла);

5) раздел для сравнения номинальной и интервальной шкал (Nominal by Interval): «эта» (Eta – коэффициент эта) и др. В файле «Вывод» статистически достоверные показатели помечены по-разному: * – на уровне p < 0,05 и ** на уровне p < 0,01.

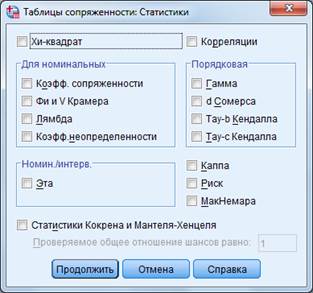
Рисунок 18 – Функционал раздела «Таблицы сопряженности: Статистики»

Практическая работа. Произвести подсчет частотных характеристик данных по шкале «возраст начала курения», построить гистограмму с наложением кривой нормального распределения. Рассчитать все описательные статистики, построить таблицы сопряженности для «пола» и «возраста».

Источник: studopedia.ru

Расчет описательных статистик в пакете STATISTICA

Рассчитаем несколько описательных статистик для ряда (4.1) с помощью пакета STATISTICA. Предполагается, что пакет инсталлирован на Вашем компьютере. Для решения задачи введем в электронную таблицу пакета исходные данные, т. е. ряд 2, 4, 6, 8, 10 как столбец. В электронной таблице пакета этот ряд будет обозначаться как VAR1. В основном меню пакета выбираем опцию «Статистика» (Statistics).

После ее активизации в ниспадающем меню выбираем опцию «Основная статистика/Таблицы» (Basic Statistics/Tables). После активизации этой опции появляется следующее окно (рис. 4.2).

Рис. 4.2. Диалоговое окно Basic Statistics and Tables (основные статистики и таблицы)

В этом окне выбираем опцию Descriptive statistics (описательные статистики). После нажатия на ОК появляется новое окно (рис. 4.3).

В этом окне, прежде всего, следует активизировать опцию Variables (переменные). После чего появляется следующее окно (рис. 4.4).

Рис. 4.4. Окно выбора переменных Select the variables for the analysis (выбор переменных для анализа)

Здесь нужно выделить мышыо первую и единственную переменную, и она появится в нижнем поле Select variables. Затем нужно нажать ОК. После этого вновь появляется диалоговое окно (см. рис. 4.3), и в нем рядом с панелью Variables (переменные) появится символ Varl. Ниже панели Variables (переменные) активизирована опция Quick (быстрый).

Следует активизировать рядом расположенную опцию Advanced (продвинутый, расширенный), просто нажав на нее мышью. В появившемся окне (рис. 4.5) следует

проставить галочки рядом с названиями: Mean (среднее), Median (медиана), Mode (мода), Standard Deviation (стандартное отклонение), Variance (дисперсия), Minimum https://studme.org/238008/matematika_himiya_fizik/raschet_opisatelnyh_statistik_pakete_statistica» target=»_blank»]studme.org[/mask_link]