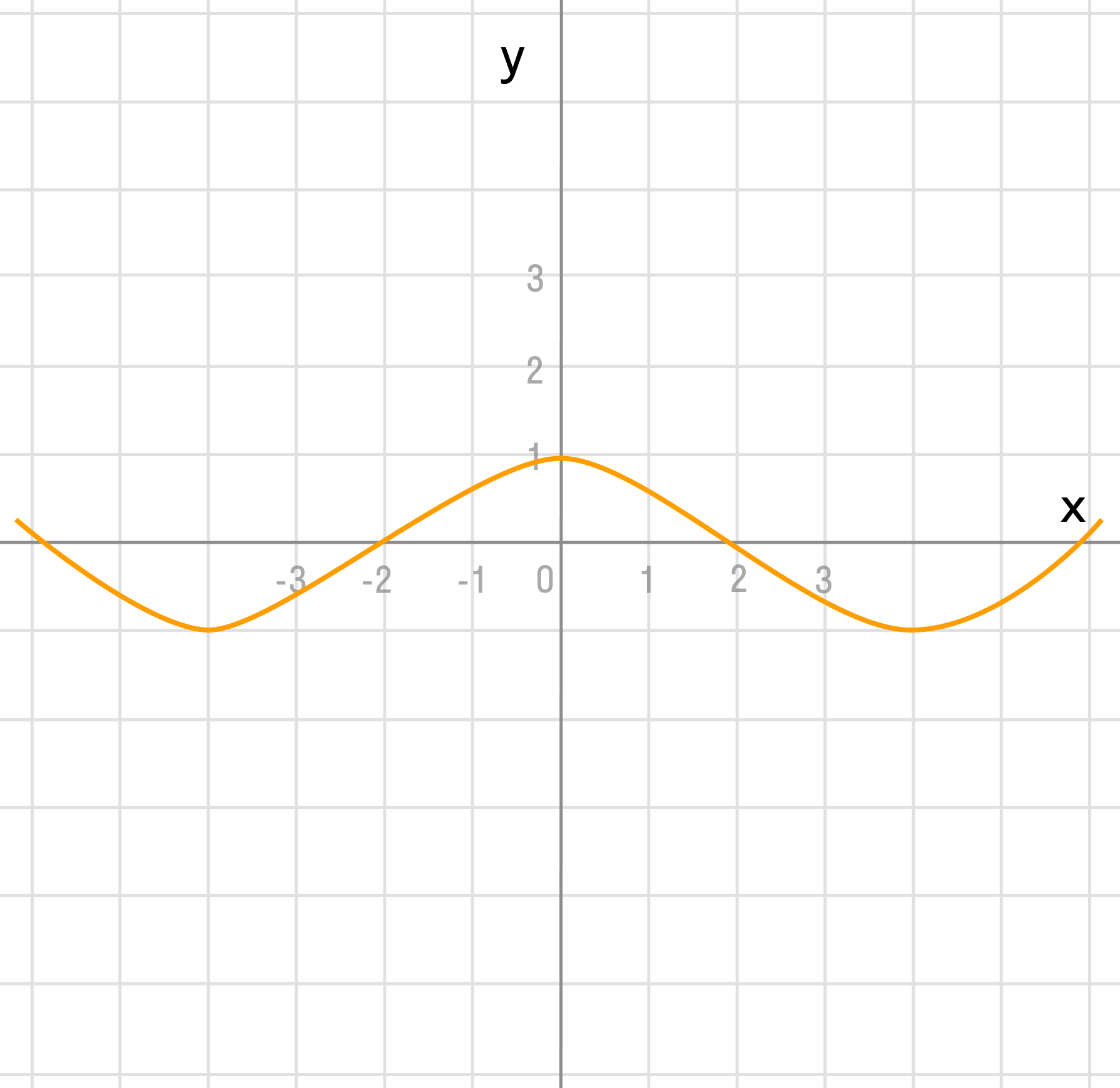
Областью определения функции называется множество всех значений аргумента при которых значение функции определено. Иными словами, если у нас задана некоторая функция , то область её определения — это все те значения которые мы можем подставить в уравнение и получить результат отличный от бесконечности и/или деления на ноль.
Найти область определения функции y=f(x) онлайн
Как найти область определения функции — примеры и способы решения
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
Функция. Область определения функции. Практическая часть. 10 класс.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
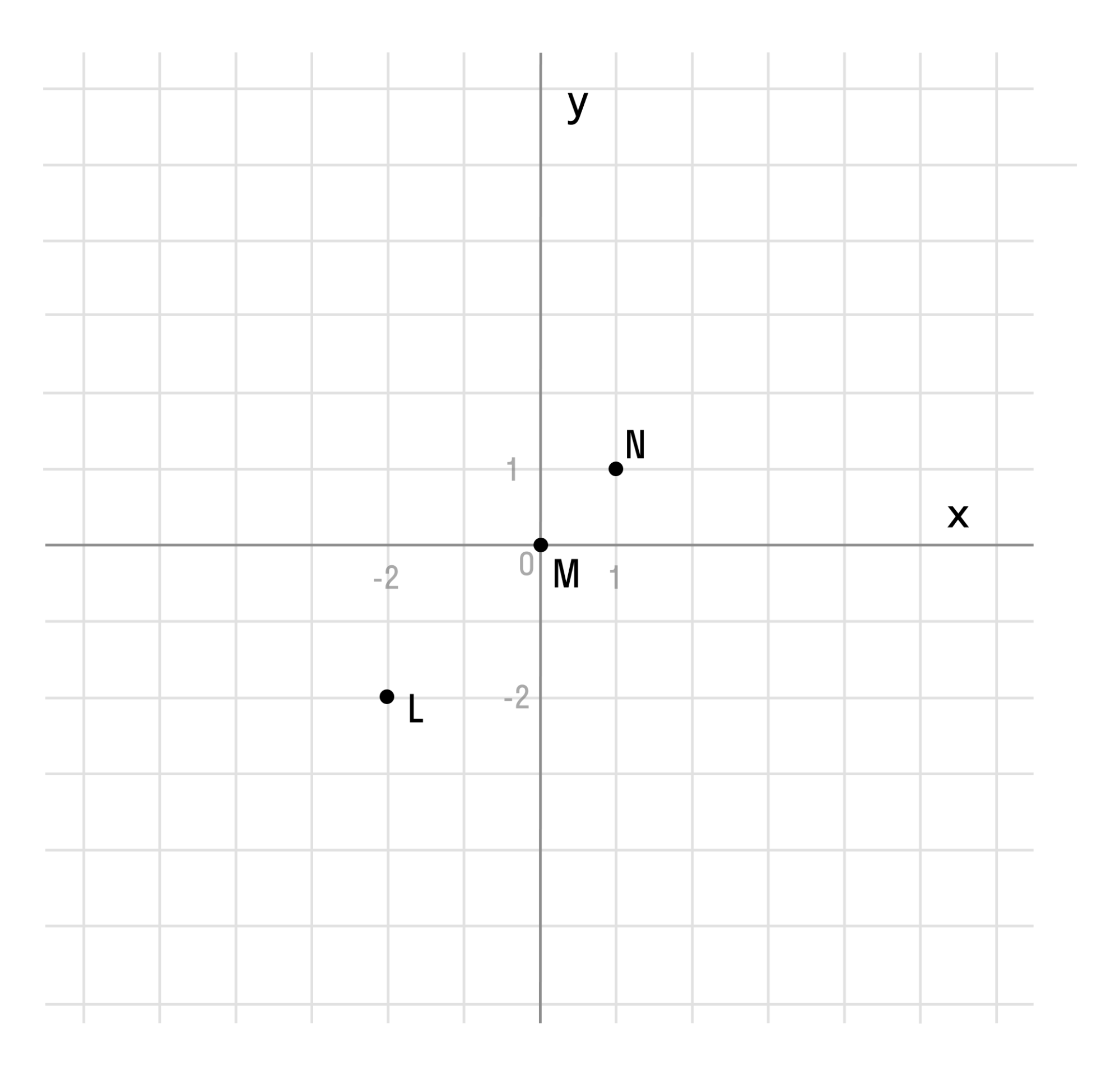
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
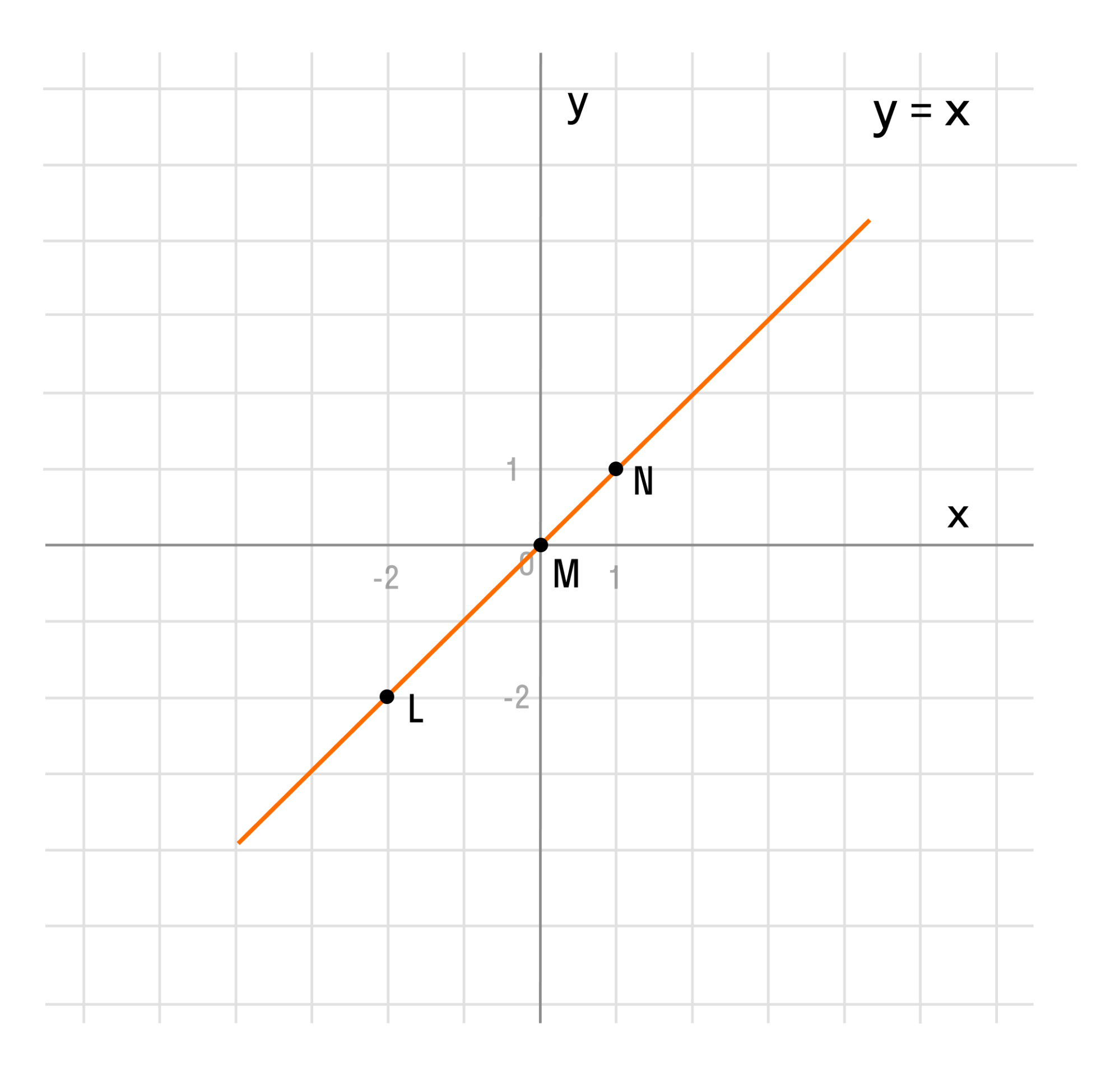
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
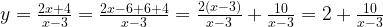
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
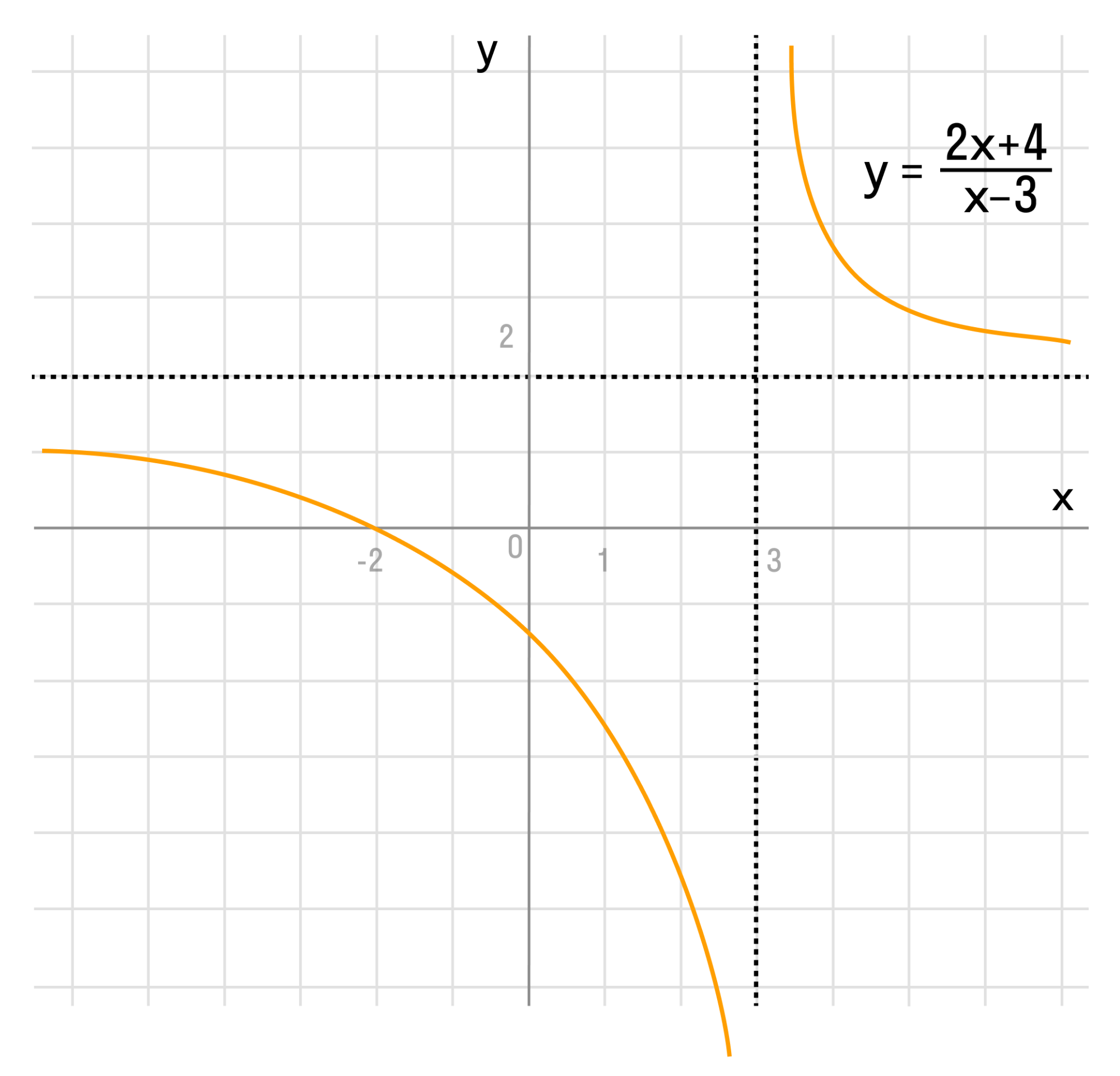
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Как найти область определения функции? #shorts










Вспомним, как параметры a, b и c определяют положение параболы.
- Ветви вниз, следовательно, a < 0. Точка пересечения с осью Oy — c = 0. Координата вершины
- Ветви вверх, следовательно, a > 0. Точка пересечения с осью Oy — c = 0. Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
- Ветви вниз, следовательно, a < 0. Точка пересечения с осью Oy — c >0. Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 4. Построить графики функций:
Воспользуемся методом построения линейных функций «по точкам».
| x | y |
| -1 | |
| 1 | 2 |
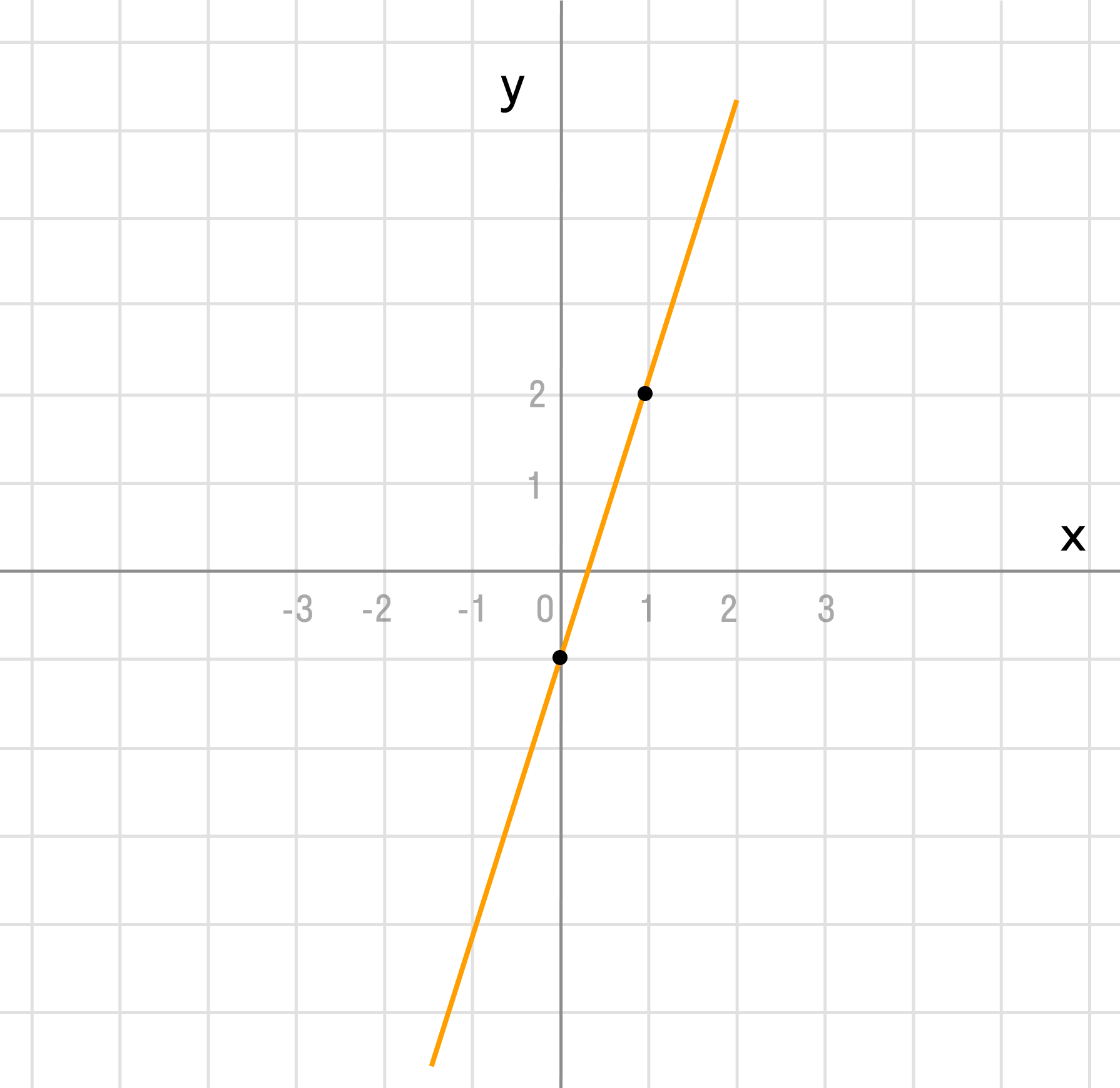
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
| x | y |
| 2 | |
| 1 | 1 |
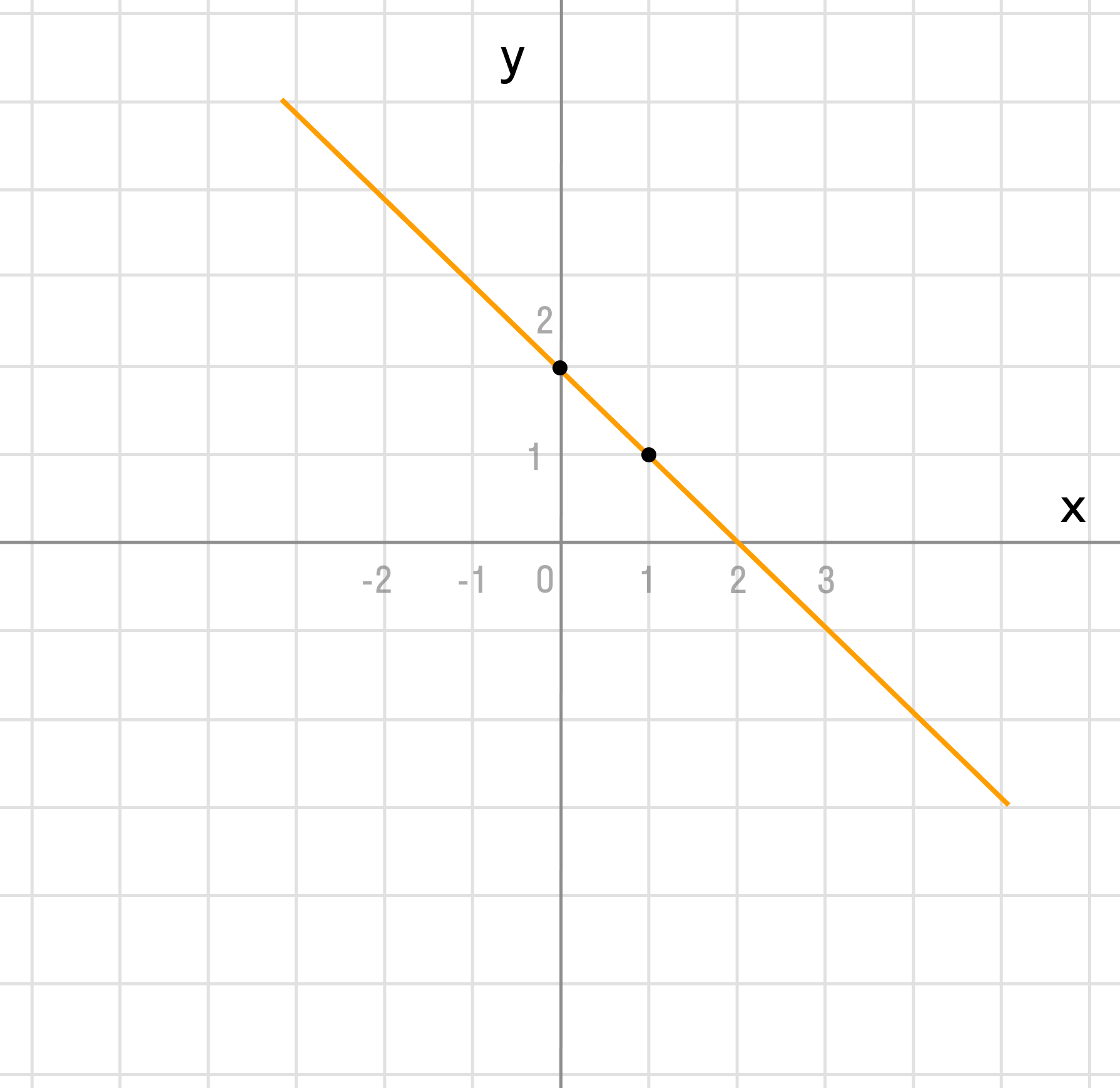
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
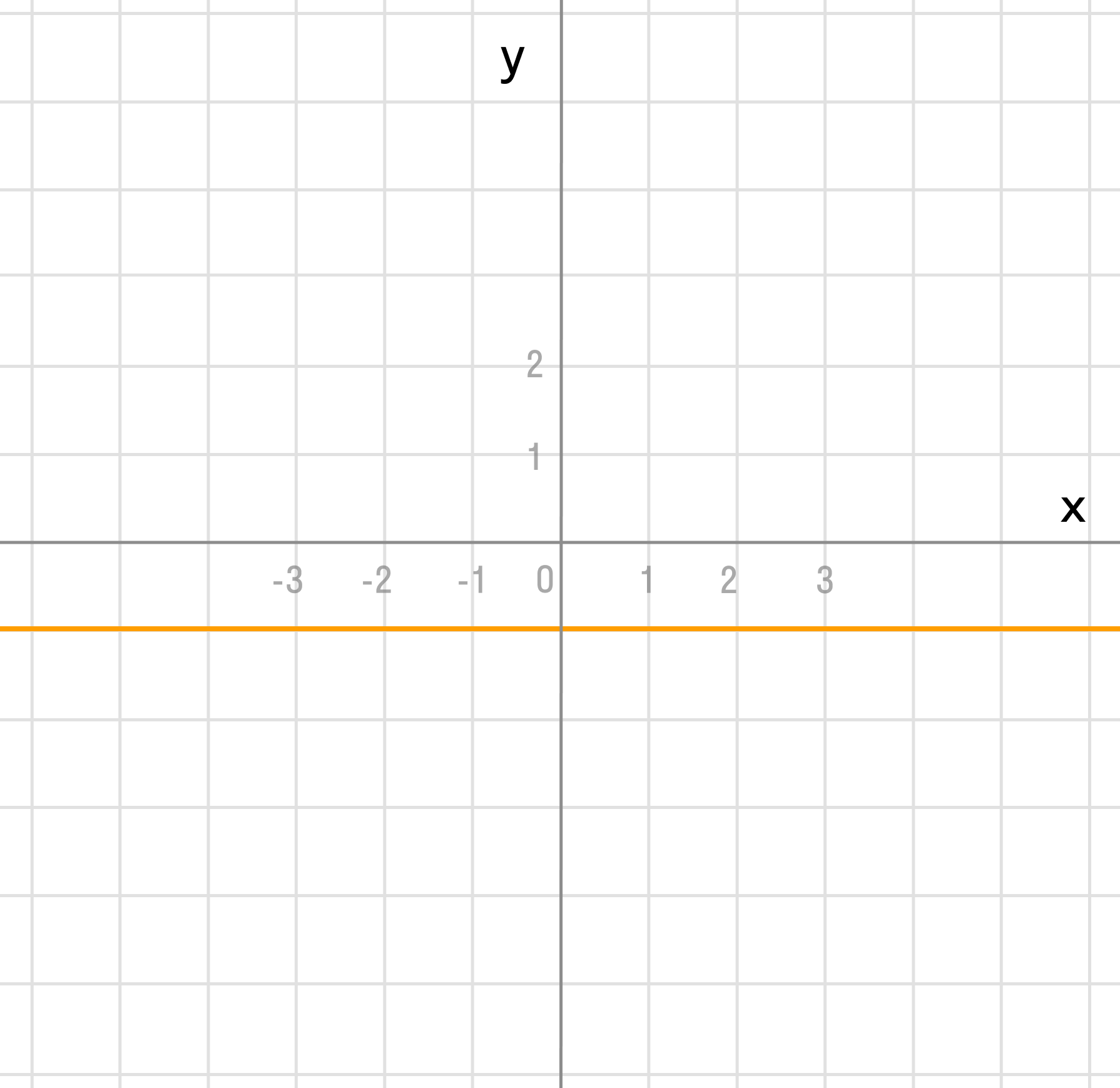
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.







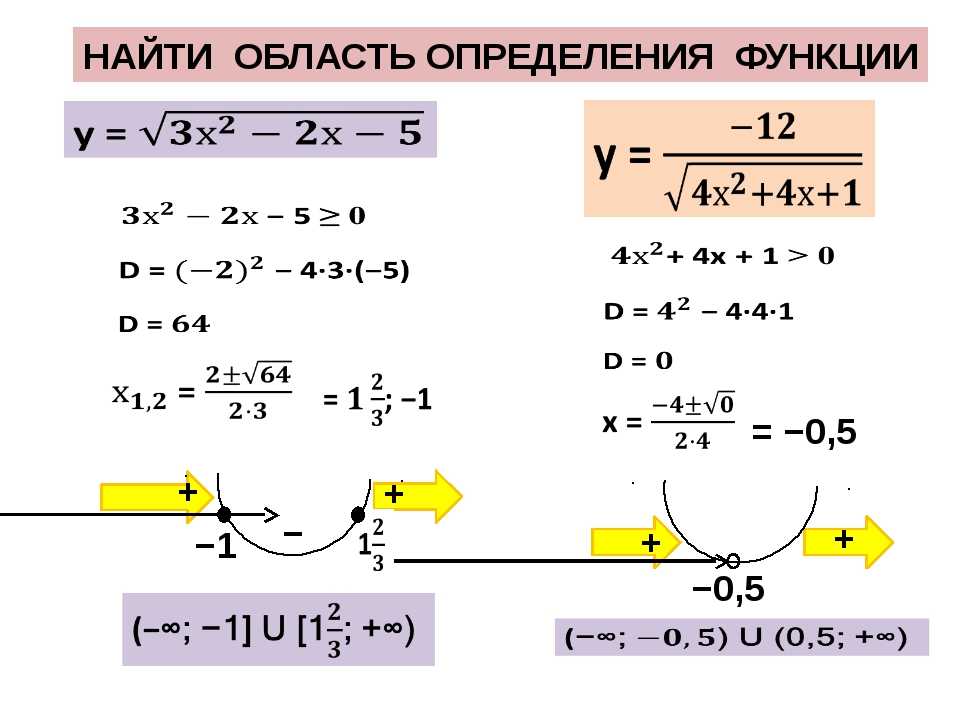


Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
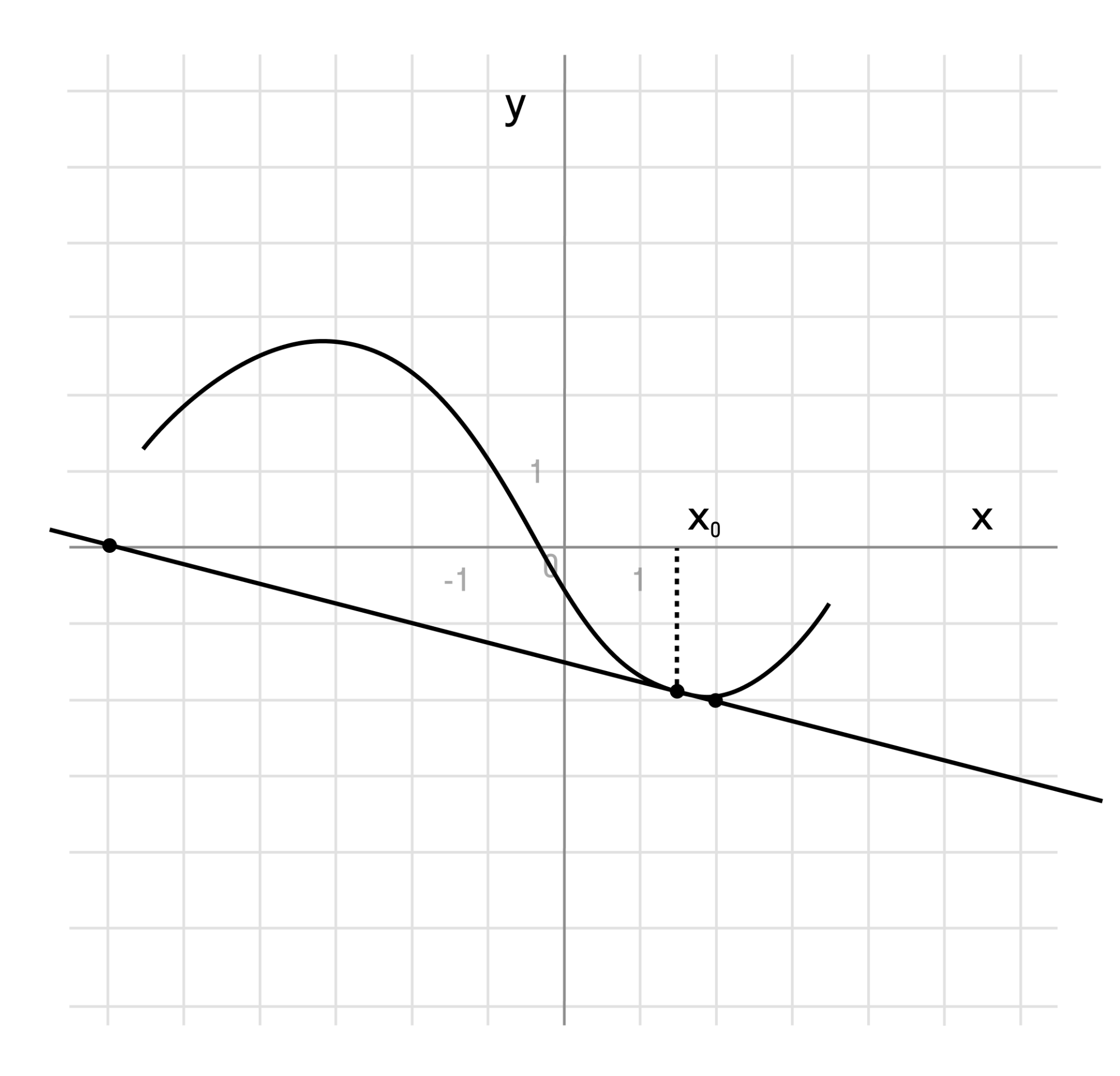
Задача 6. Построить графики функций:
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
Преобразование в одно действие типа f(x) + a.
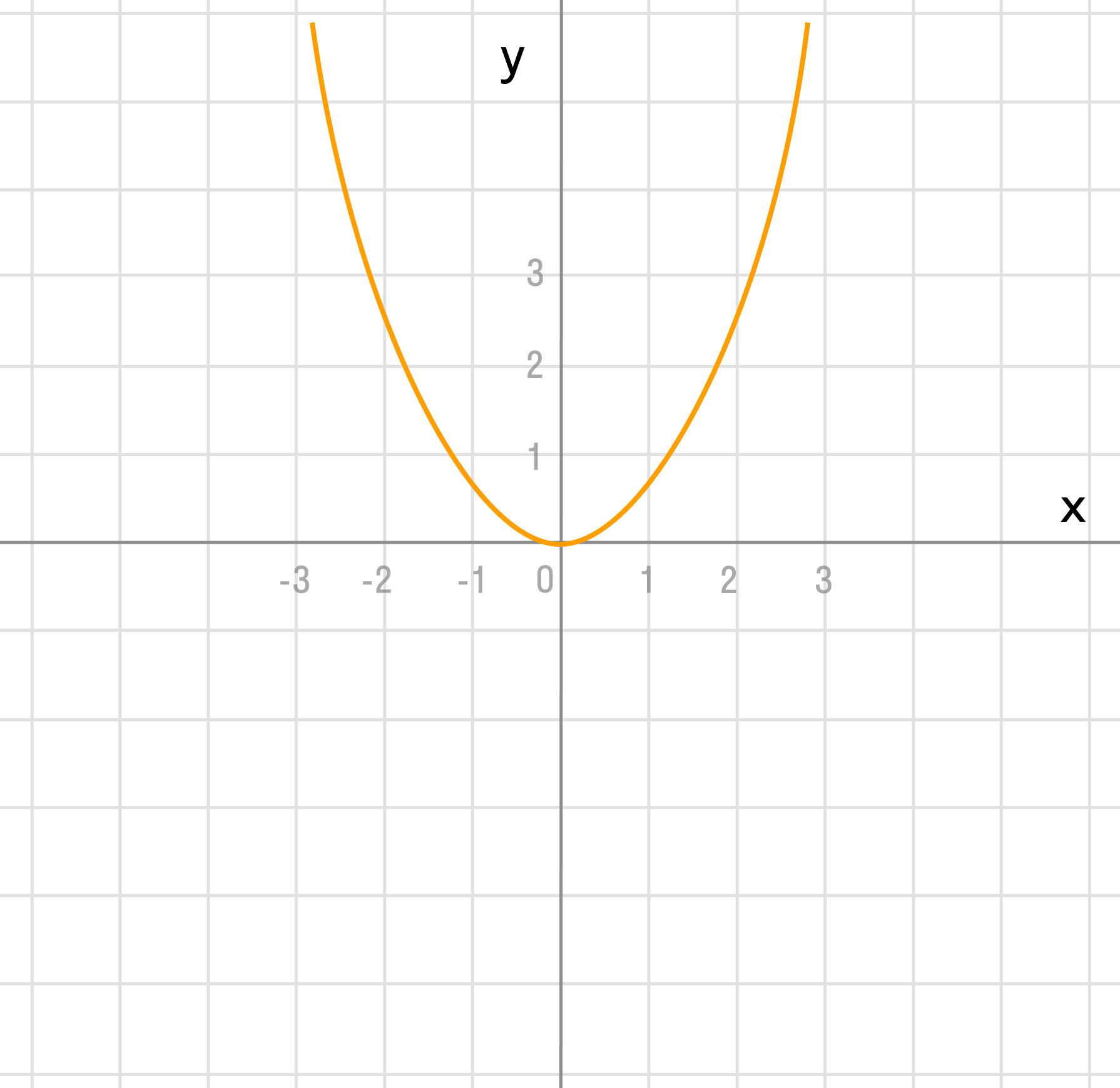
Сдвигаем график вверх на 1:
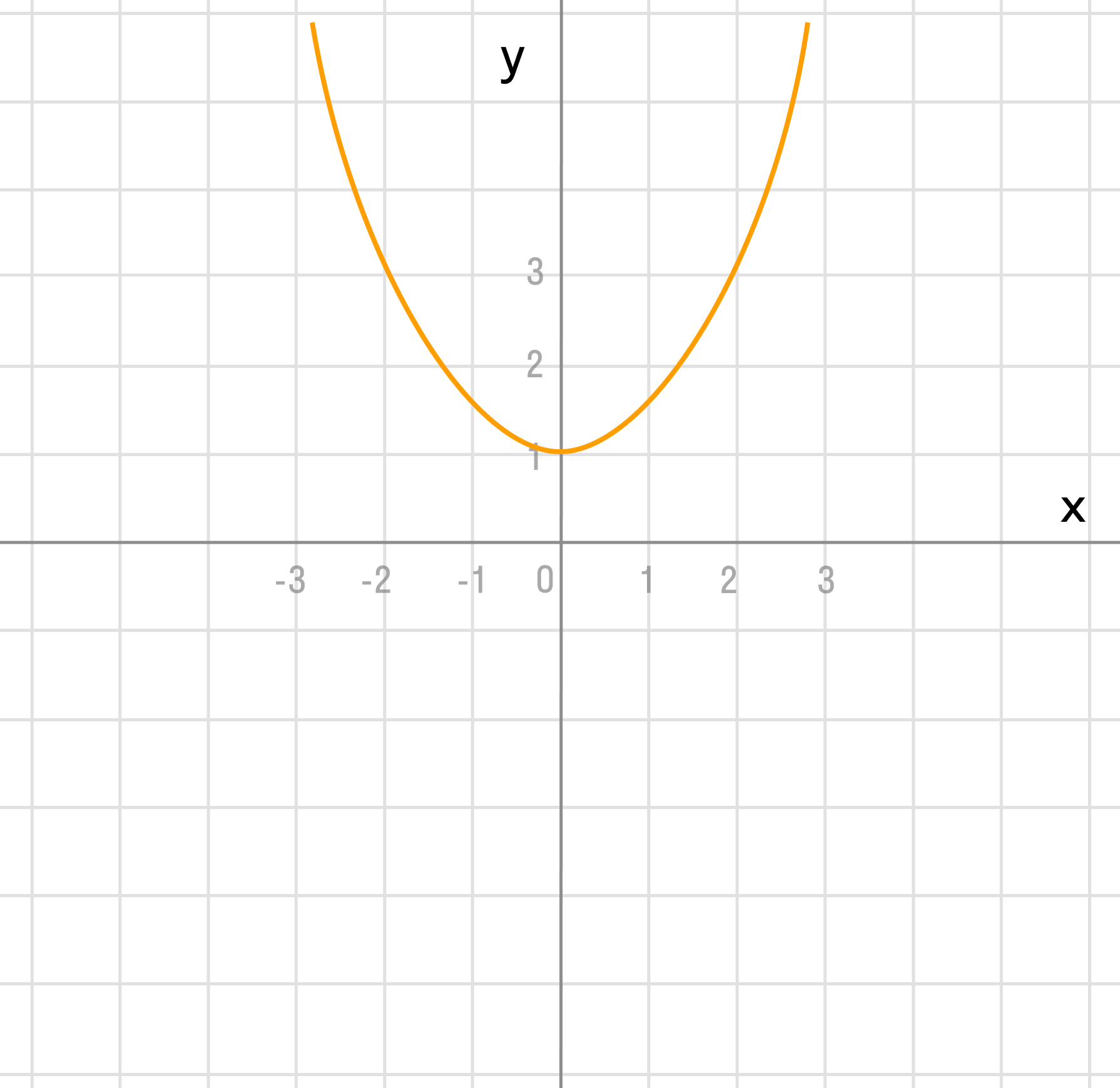
Преобразование в одно действие типа f(x — a).
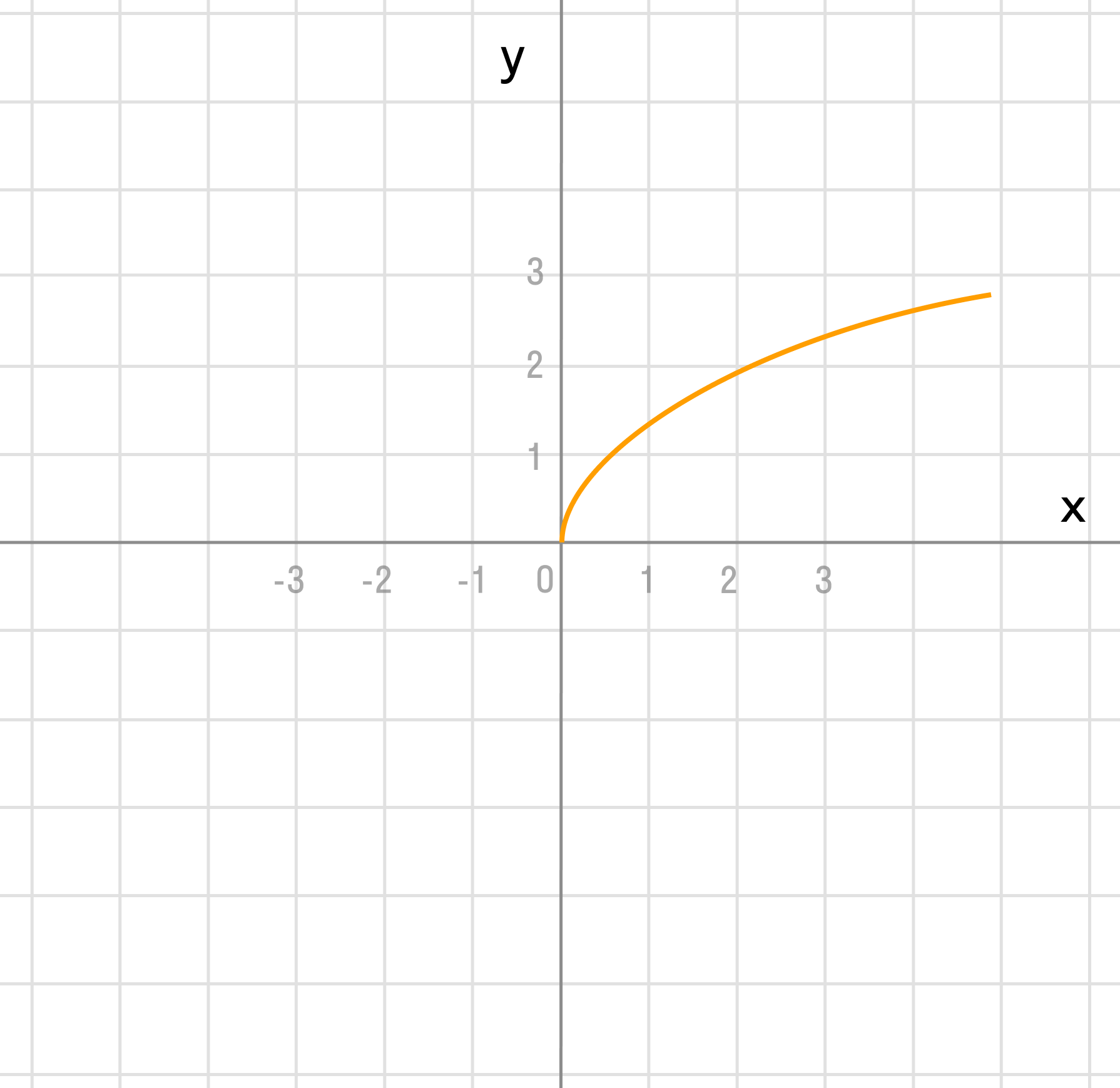
Сдвигаем график вправо на 1:
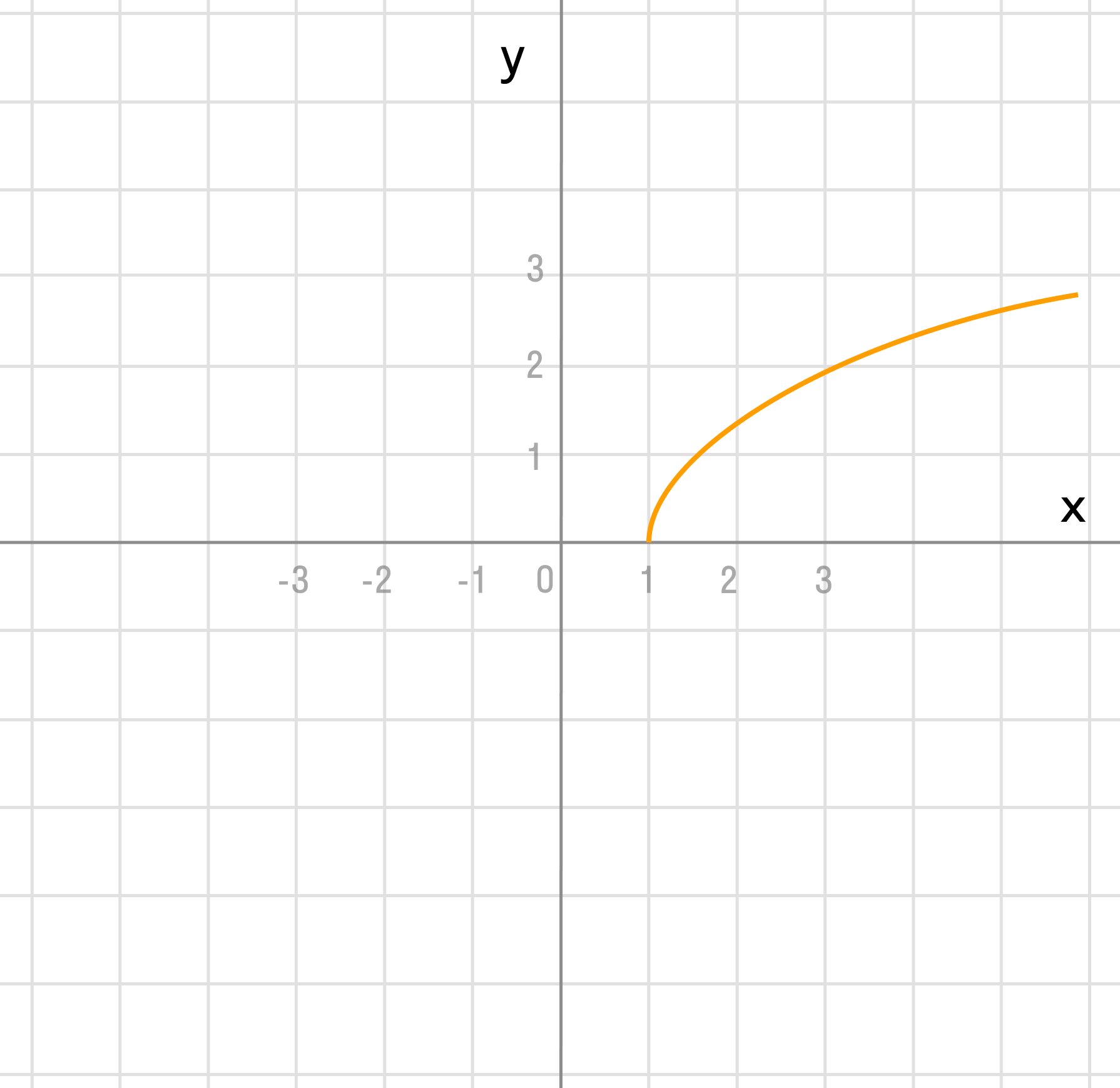
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
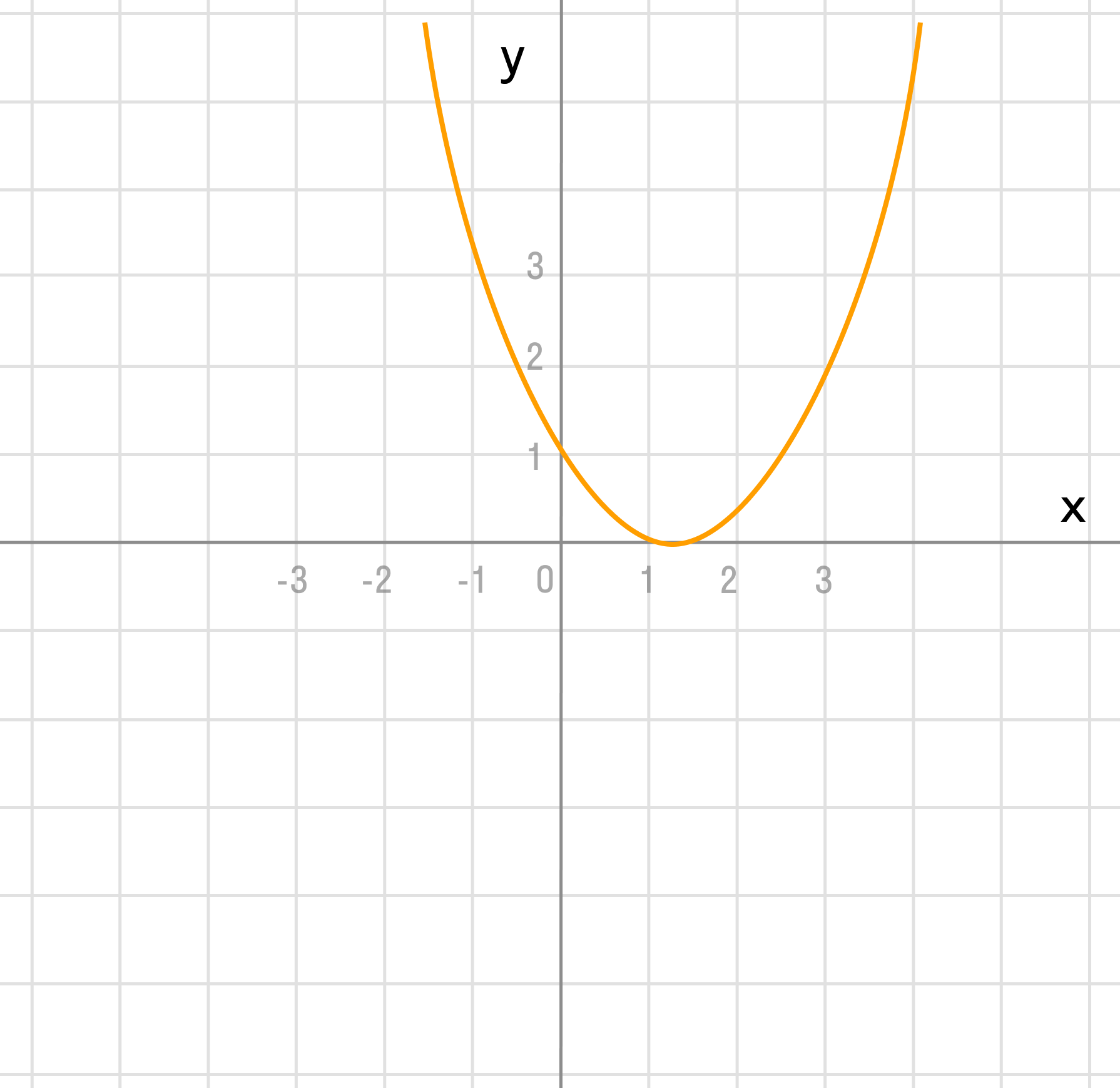
Сдвигаем график вверх на 2:
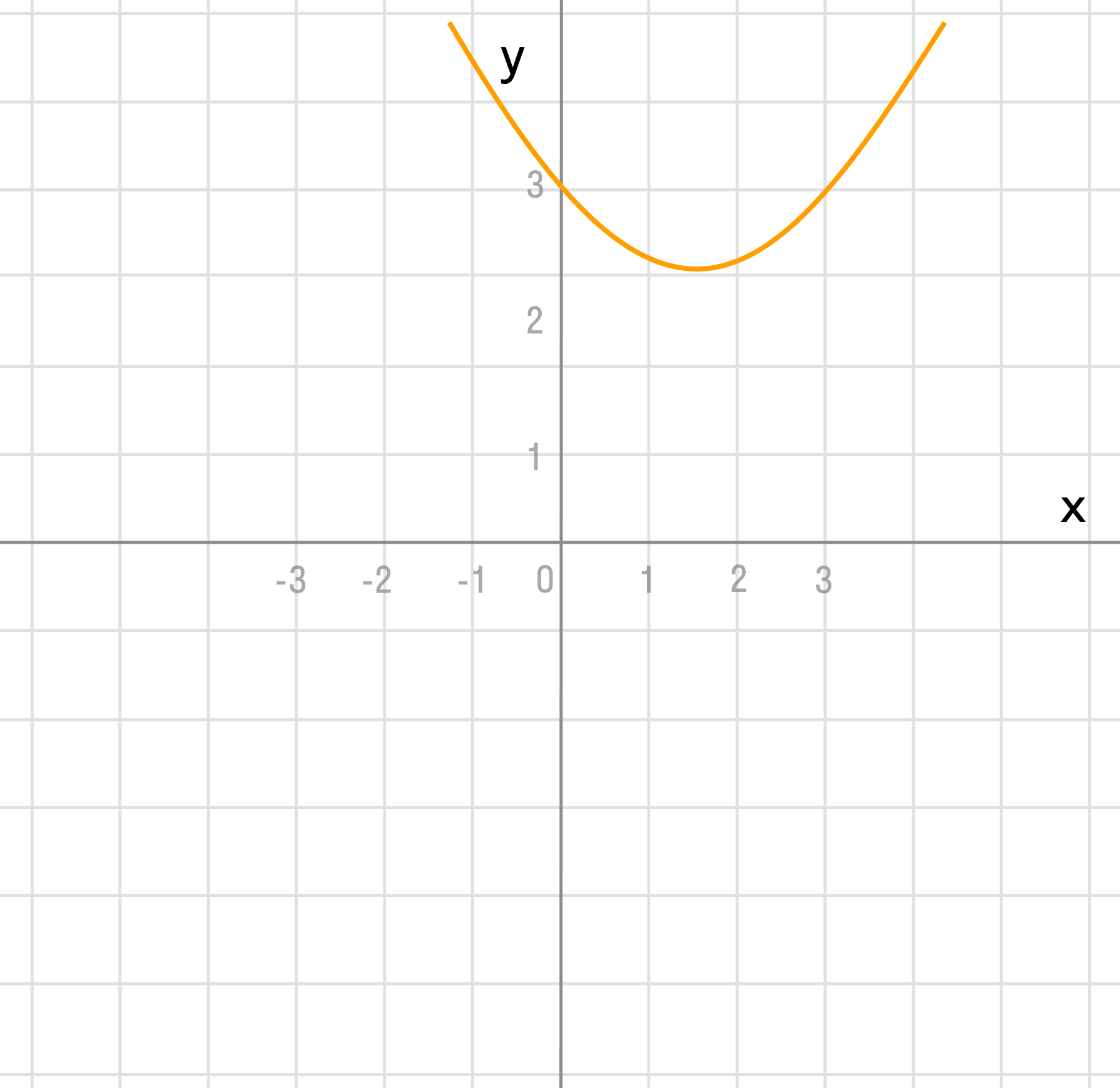
Преобразование в одно действие типа
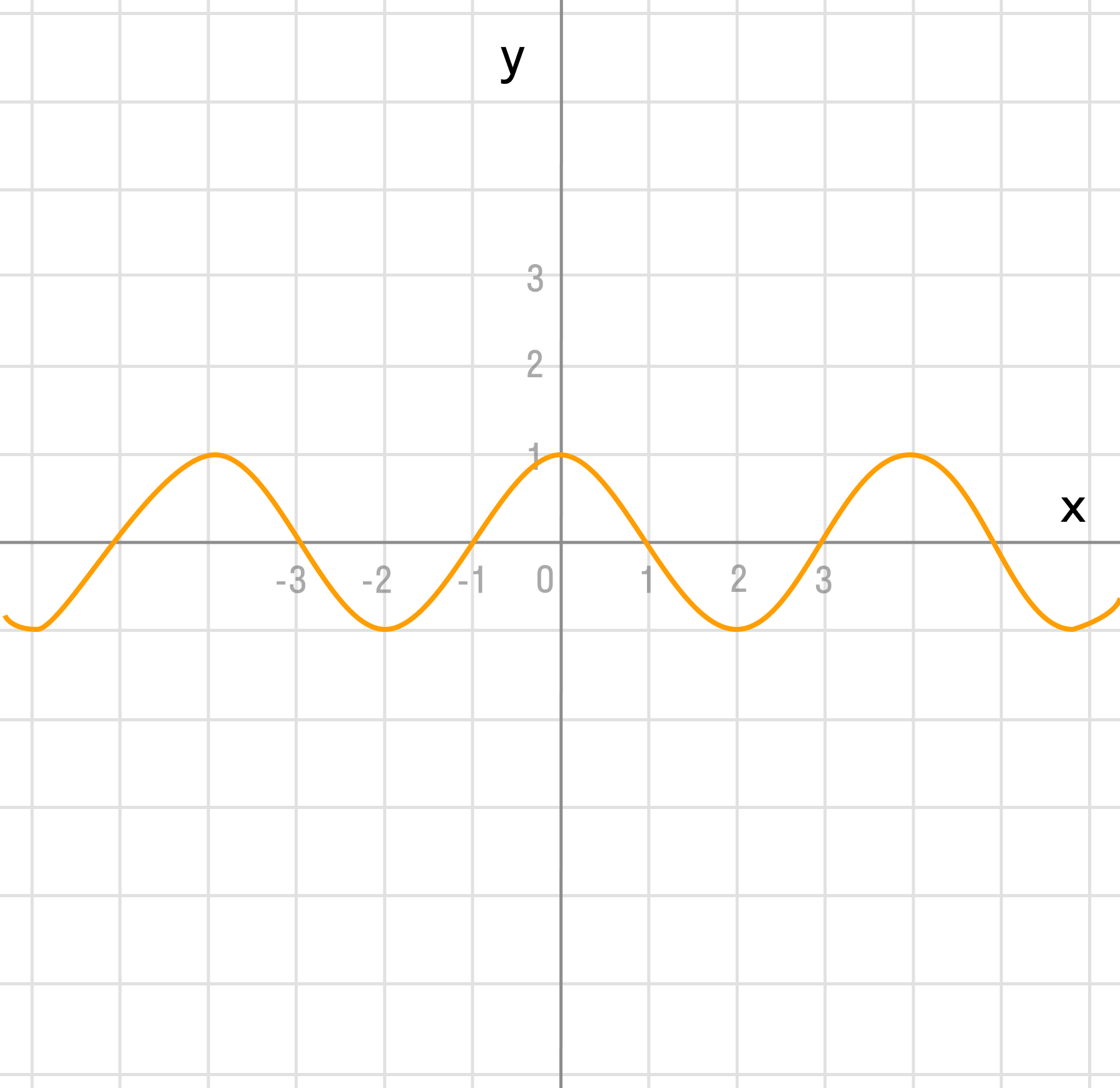
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс: