Не каждый из школьников может похвастаться хорошими знаниями в области алгебры и геометрии. Но при этом становиться круглым троечником по предмету не хочется. Как ни старайся понять эти формулы и теоремы, ничего не выходит. В этих случаях есть выход. Можно получать неплохие оценки, если знать как решать задачи геометрии по фотографии.
Для этого в интернете есть специальные сервисы, о которых мы не только расскажем, но и объясним как пользоваться.
Перейти к онлайн-сервису Mathway
Photomath — решает задачи по фото
Приложение под названием Photomath широко распространено среди учащихся школ и институтов. Установить его можно на смартфон на ОС Android и IOS, и всегда воспользоваться, когда это необходимо. Весь функционал полностью бесплатный, а благодаря простому и понятному интерфейсу во время работы с программой не возникнет сложностей. С помощью Photomath можно решить огромное количество задач и уравнений, вписывать их вручную, редактировать, а также узнавать ответы с помощью фото. Что понадобится для решения задач?
ОКСИДЫ, КИСЛОТЫ, СОЛИ И ОСНОВАНИЯ ХИМИЯ 8 класс / Подготовка к ЕГЭ по Химии — INTENSIV

-
В первую очередь установите приложение из Play Маркет или App Store на свой телефон и запустите.

Выберите язык интерфейса. По умолчанию будет предложен Русский, но если необходим другой, нажмите на кнопку «Прочее».

Прочитайте инструкцию, которую предложит программа, либо нажмите кнопку «Пропустить», если считаете, что самостоятельно разберётесь со всеми возможностями.

Установите свой возраст. Приложение не ограничено по возрастной категории.

Теперь отметьте кем вы являетесь. На выбор есть – родитель, ученик или учитель.

После приложение запросит доступ к камере вашего устройства, нажмите «Разрешить». Это действий необходимо для того, чтобы решать уравнения с помощью фото.
Через несколько секунд программа предоставит вам готовый результат, а ответ вы сможете вписать себе.
Геометрия — отличный решебник с формулами
Геометрия, или второе название, Pocket Edition – это ещё одно приложение для мобильных устройств, которое обязательно вам поможет. Это не просто справочник или решебник, это целое образовательное приложение, которое сможет помочь с решением геометрии всего школьного курса.
Уменьшаемое вычитаемое разность. Математика 1 класс

Главная особенность программы – ваш экран смартфона, словно тетрадный лист, на котором вам предстоит нарисовать поставленную задачу.
Pocket Edition обладает простым интерфейсом. Снизу на панели вы увидите несколько кнопок:
- Инструменты рисования;
- Инструменты выделения;
- Инструменты связи;
- Запуск решения или создание новой задачи.
Уже после того, как вы выберите нужный вам раздел, высветился ещё несколько дополнительных функций. Именно с их помощью пользователь и должен наглядно изобразить поставленную перед ним задачу по геометрии.
Ученики и студенты знают, что в геометрии важен не просто результат. Каждую теорему нужно доказать и объяснить. Разработчики учли все эти моменты и создали идеальное приложение. Оно в логической последовательности даёт ответы и показывает полученные выводы.

Каждый шаг сопровождается иллюстрациями, доводами и обоснованиями. Также, приложение подскажет как подойти к противоречию, если определенную теорему нельзя доказать.

Геометрия доступна в App Store и в Play Маркете. Скачать можно бесплатно, также как в бесплатном доступе вы сможете лишь попробовать для решения одну задачу. В целом, этого достаточно, чтобы ознакомиться с функционалом. Если вы планируете постоянно пользоваться данной программой, придется платить деньги. Pocket Edition станет настоящей палочкой-выручалочкой на экзамене.
Mathway — приложения для решения задач по фото
Mathway – ещё одно умное приложение для смартфонов. Если вы предпочитаете использовать настольный компьютер или ноутбук, то можно воспользоваться веб-версией сайта, правда за символическую оплату.
На телефон же скачать приложение можно бесплатно из App Store и Play Market. Разработчики – опытные программисты, а само приложение способно решить задачи разной сложности, как по фотографии, так и если введёте уравнения вручную.
Чтобы воспользоваться возможностями, нужно:

-
Скачать и установить приложение на свой смартфон, запустить.
Mathway не просто даёт готовый ответ, а прописывает каждое действие последовательно. В итоге получается развернутое решение.
В приложении доступно решение задач по начальной математике, алгебре, тригонометрии, конечной математики, математический анализ, построение графиков, химия, статистика и начало анализа.
Видео
Заключение
Пользуйтесь данными сервисами, если нужна помощь с домашним заданием или на контрольной работе. Но не увлекайтесь, ведь знания – сила, а учиться можно всю жизнь
Источник: iziplus.ru
Поиск решений
Мощным средством анализа данных Excel является надстройка Solver (Поиск решения). С ее помощью можно определить, при каких значениях указанных влияющих ячеек формула в целевой ячейке принимает нужное значение (минимальное, максимальное или равное какой-либо величине).
Для процедуры поиска решения можно задать ограничения, причем не обязательно, чтобы при этом использовались те же влияющие ячейки. Для расчета заданного значения применяются различные математические методы поиска. Вы можете установить режим, в котором полученные значения переменных автоматически заносятся в таблицу. Кроме того, результаты работы программы могут быть оформлены в виде отчета. Программа Поиск решений (в оригинале Excel Solver) – дополнительная надстройка табличного процессора MS Excel, которая предназначена для решения определенных систем уравнений, линейных и нелинейных задач оптимизации,
По умолчанию в Excel надстройка Поиск решения отключена. Чтобы активизировать ее в Excel 2007, щелкните значок Кнопка Microsoft Office , щелкните Параметры Excel, а затем выберите категорию Надстройки. В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти. В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.

Процедура поиска решения
1. Создайте таблицу с формулами, которые устанавливают связи между ячейками.
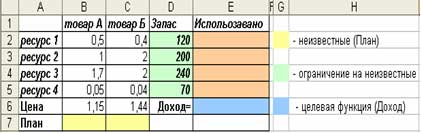
2. Выделите целевую ячейку, которая должна принять необходимое значение, и выберите команду:
В Excel 2007 Данные/Анализ/Поиск решения;
Поле Set Target Cell (Установить целевую ячейку) открывшегося диалогового окна надстройки Solver (Поиск решения) будет содержать адрес целевой ячейки.
3. Установите переключатели Equal To (Равной), задающие значение целевой ячейки, — Мах (максимальному значению), Min (минимальному значению) или Value of (значению). В последнем случае введите значение в поле справа.
4. Укажите в поле By Changing Cells (Изменяя ячейки), в каких ячейках программа должна изменять значения в поисках оптимального результата.
5. Создайте ограничения в списке Subject to the Constraints (Ограничения). Для этого щелкните на кнопке Add (Добавить) и в диалоговом окне Add Constraint (Добавление ограничения) определите ограничение.

6. Щелкните на кнопке на кнопке Options (Параметры), и в появившемся окне установите переключатель Неотрицательные значения (если переменные должны быть позитивными числами), Линейная модель (если задача, которую вы решаете, относится к линейным моделям)
7. Щелкнув на кнопке Solver (Выполнить), запустите процесс поиска решения.
8. Когда появится диалоговое окно Solver Results (Результаты поиска решения), выберите переключатель Keep Solve Solution (Сохранить найденное решение) или Restore Original Values (Восстановить исходные значения). 9. Щелкните на кнопке ОК.
Параметры средства Поиск решения
Максимальное время — служит для ограничения времени, отпущенного на поиск решения задачи. В этом поле можно ввести время в секундах, не превышающее 32 767 (примерно девять часов); значение 100, используемое по умолчанию, вполне приемлемо для решения большинства простых задач.

Предельное число итераций — управляет временем решения задачи путем ограничения числа вычислительных циклов (итераций). Относительная погрешност — определяет точность вычислений. Чем меньше значение этого параметра, тем выше точность вычислений.
Допустимое отклонение — предназначен для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. Чем больше значение допуска, тем меньше времени требуется на поиск решения. Сходимость — применяется только к нелинейным задачам.
Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Линейная модель — служит для ускорения поиска решения путем применения к задаче оптимизации линейной модели.
Нелинейные модели предполагают использование нелинейных функций, фактора роста и экспоненциального сглаживания, что замедляет вычисления. Неотрицательные значения — позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых не было задано соответствующее ограничение в диалоговом окне Добавить ограничение.
Автоматическое масштабирование — используется, когда числа в изменяемых ячейках и в целевой ячейке существенно различаются. Показывать результаты итераций — приостанавливает поиск решения для просмотра результатов отдельных итераций.
Загрузить модель — после щелчка на этой кнопке отрывается одноименное диалоговое окно, в котором можно ввести ссылку на диапазон ячеек, содержащих модель оптимизации. Сохранить модель — служит для отображения на экране одноименного диалогового окна, в котором можно ввести ссылку на диапазон ячеек, предназначенный для хранения модели оптимизации.
Оценка линейная — выберите этот переключатель для работы с линейной моделью. Оценка квадратичная — выберите этот переключатель для работы с нелинейной моделью. Разности прямые — используется в большинстве задач, где скорость изменения ограничений относительно невысока. Увеличивает скорость работы средства Поиск решения.
Разности центральные — используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдано сообщение о том, что получить более точное решение не удается. Метод поиска Ньютона — требует больше памяти, но выполняет меньше итераций, чем в методе сопряженных градиентов. Метод поиска сопряженных градиентов — реализует метод сопряженных градиентов, для которого требуется меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно большая и необходимо экономить память или если итерации дают слишком малое отличие в последовательных приближениях.
Источник: studfile.net
Программа найдите и назовите решение
= Мир MS Excel/Статьи об Excel
МЕНЮ САЙТА
Информация о сайте
Развите сайта
Приемы работы
Инструменты и настройки
Интеграция
Готовые решения
Вопросы и решения
Работа и общение
Работа форума и сайта
Библиотека
Книги по Excel
Книги по VBA
Видеосалон
Справочники
Разработчик
КАТЕГОРИИ РАЗДЕЛА
| Приёмы работы с книгами, листами, диапазонами, ячейками [6] |
| Приёмы работы с формулами [13] |
| Настройки Excel [3] |
| Инструменты Excel [4] |
| Интеграция Excel с другими приложениями [4] |
| Форматирование [1] |
| Выпадающие списки [2] |
| Примечания [1] |
| Сводные таблицы [1] |
| Гиперссылки [1] |
| Excel и интернет [1] |
| Excel для Windows и Excel для Mac OS [2] |
Поиск решения
Большинство задач, решаемых с помощью электронной таблицы, предполагают нахождение искомого результата по известным исходным данным. Но в Excel есть инструменты, позволяющие решить и обратную задачу: подобрать исходные данные для получения желаемого результата.
Одним из таких инструментов является Поиск решения , который особенно удобен для решения так называемых «задач оптимизации».
Если Вы раньше не использовали Поиск решения , то Вам потребуется установить соответствующую надстройку.
Сделать это можно так:
для версий старше Excel 2007 через команду меню Сервис —> Надстройки;
начиная с Excel 2007 через диалоговое окно Параметры Excel
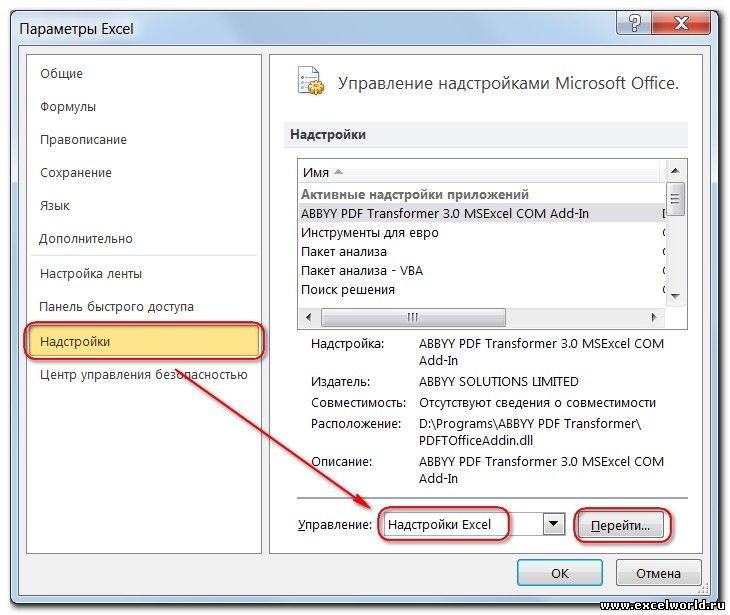
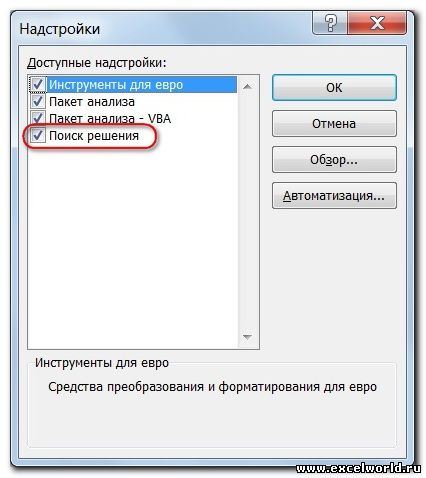
Начиная с версии Excel 2007 кнопка для запуска Поиска решения появится на вкладке Данные .
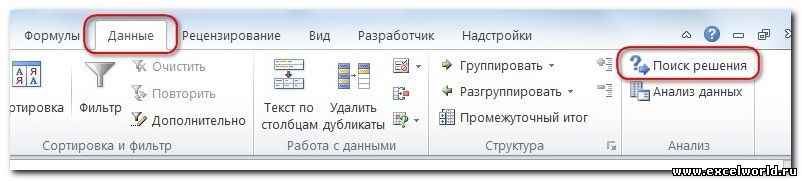
В версиях до Excel 2007 аналогичная команда появится в меню Сервис
Разберём порядок работы Поиска решения на простом примере.
Пример 1. Распределение премии
Предположим, что Вы начальник производственного отдела и Вам предстоит по-честному распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.
Первым делом создаём таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат — это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).
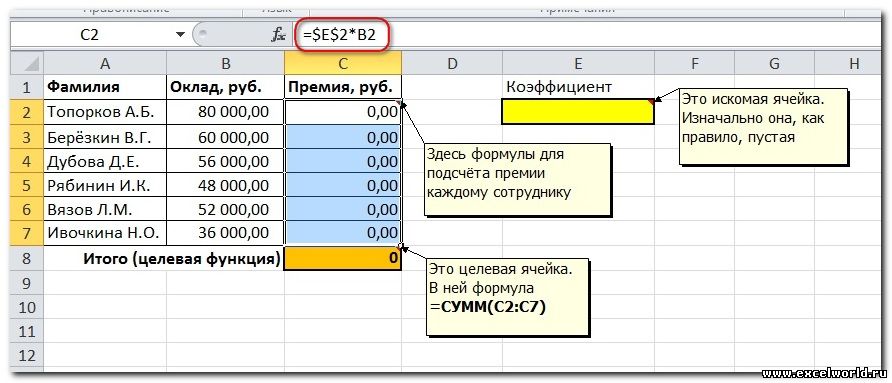
Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:
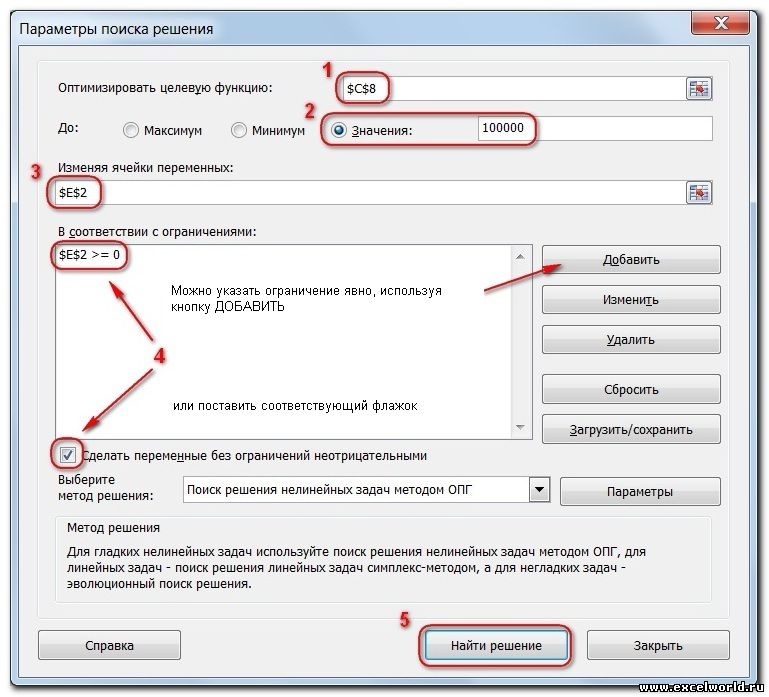
Начиная с Excel 2010
До Excel 2010
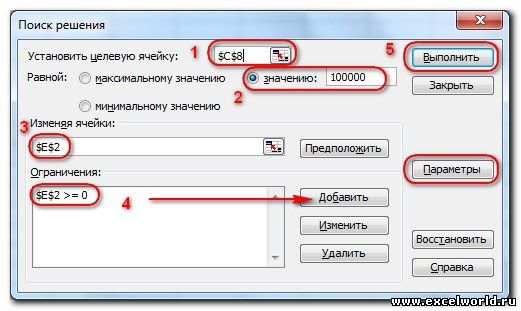
- Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна
- Варианты оптимизации: максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода
- Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение
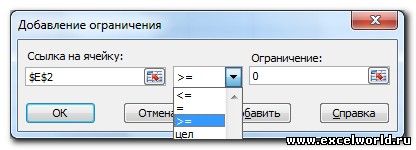
- Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимо всем понятных знаков =, >=, цел (целое), бин (бинарное или двоичное, т.е. 0 или 1), раз (все разные — только начиная с версии Excel 2010).
В данном примере ограничение только одно: коэффициент должен быть положительным. Это ограничение можно задать по-разному: либо установить явно, воспользовавшись кнопкой Добавить, либо поставить флажок Сделать переменные без ограничений неотрицательными.
Для версий до Excel 2010 этот флажок можно найти в диалоговом окне Параметры Поиска решения, которое открывается при нажатии на кнопку Параметры
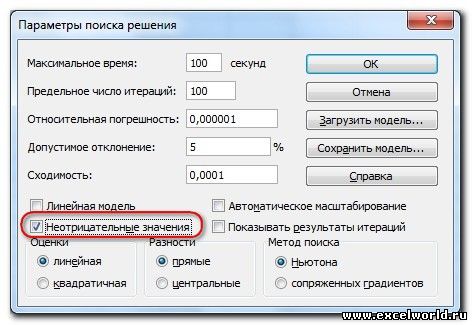
После нажатия кнопки Найти решение (Выполнить) Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.
Начиная с Excel 2010
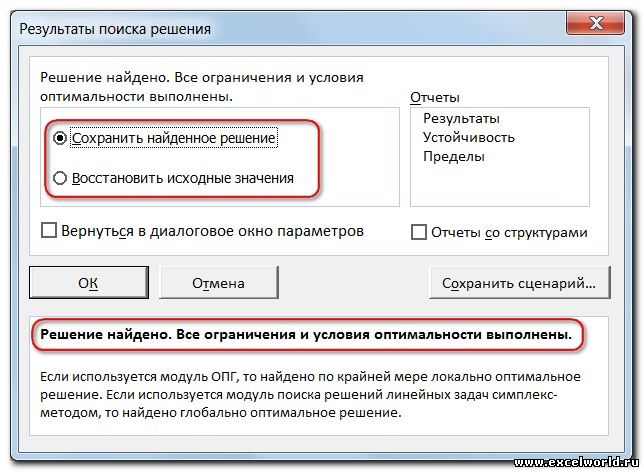
До Excel 2010
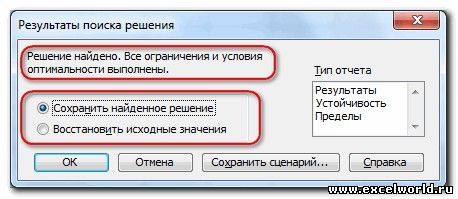
Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОК и фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена и возвращаетесь к предыдущему состоянию таблицы.
Решение данной задачи выглядит так
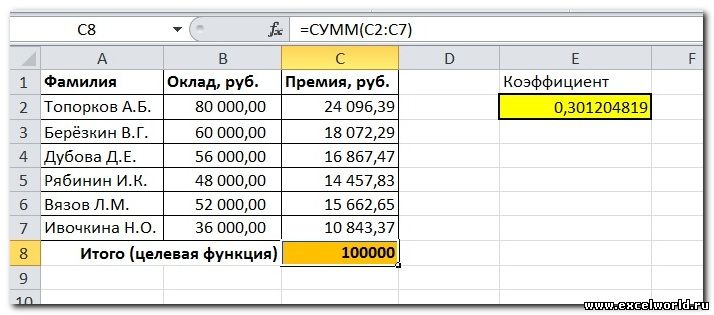
Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.
Разберём еще одну задачу оптимизации (получение максимальной прибыли)
Пример 2. Мебельное производство (максимизация прибыли)
Фирма производит две модели А и В сборных книжных полок.
Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.
Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В — 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю.
Для каждого изделия модели А требуется 12 мин машинного времени , а для изделия модели В — 30 мин. в неделю можно использовать 160 ч машинного времени.
Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В — 120 руб. прибыли?
Порядок действий нам уже известен.
Сначала создаем таблицы с исходными данными и формулами. Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно автору. Например, как на рисунке
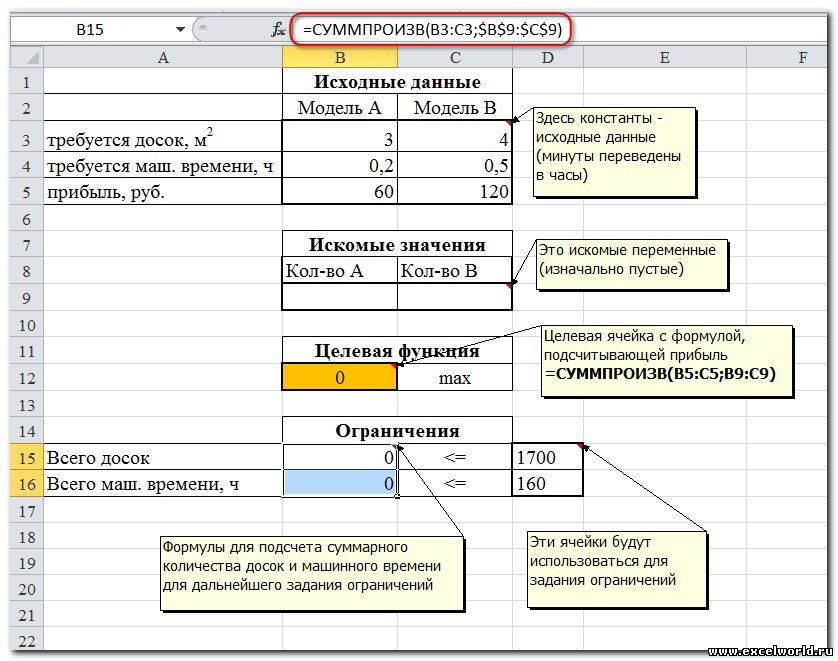
Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры
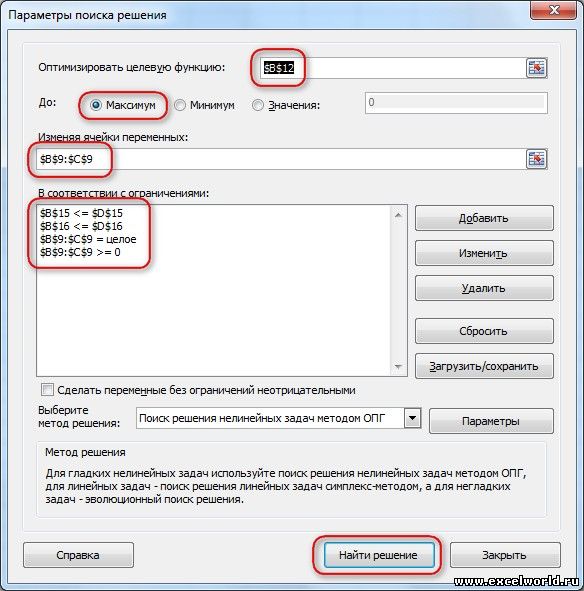
- Целевая ячейка B12 содержит формулу для расчёта прибыли
- Параметр оптимизации — максимум
- Изменяемые ячейки B9:C9
- Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице
- Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат
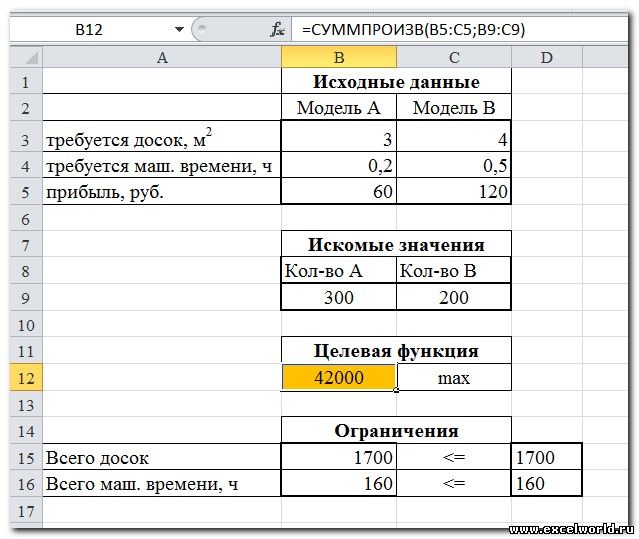
Но даже если Вы правильно создали формулы и задали ограничения, результат может оказаться неожиданным. Например, при решении данной задачи Вы можете увидеть такой результат:
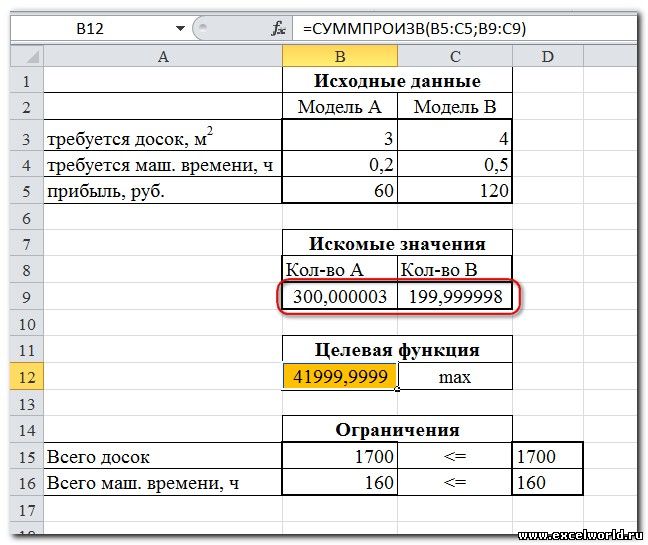
И это несмотря на то, что было задано ограничение целое. В таких случаях можно попробовать настроить параметры Поиска решения. Для этого в окне Поиск решения нажимаем кнопку Параметры и попадаем в одноимённое диалоговое окно
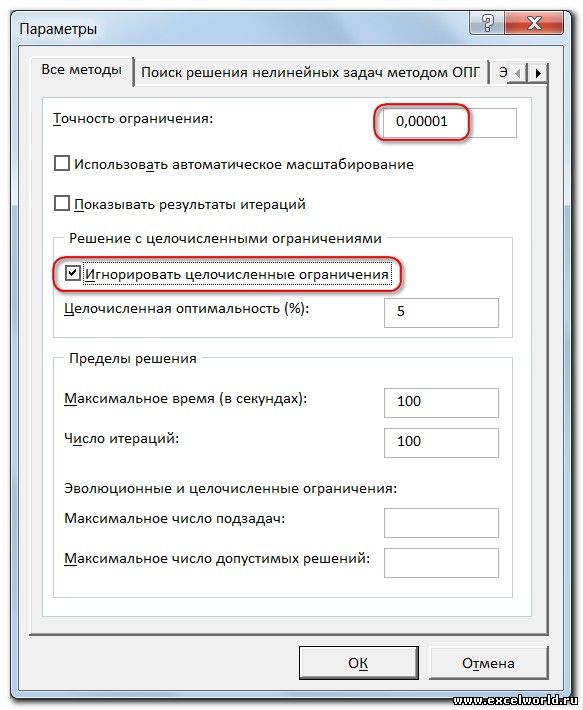
Первый из выделенных параметров отвечает за точность вычислений. Уменьшая его, можно добиться более точного результата, в нашем случае — целых значений. Второй из выделенных параметров (доступен, начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться дробные результаты при ограничении целое ? Оказывается Поиск решения это ограничение просто проигнорировал в соответствии с установленным флажком.
Пример 3. Транспортная задача (минимизация затрат)
На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на доставку включается в себестоимость объекта, поэтому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом.
Дано: запасы песка на карьерах; потребности в песке стройплощадок; затраты на транспортировку между каждой парой «поставщик-потребитель».
Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при которой общие затраты на транспортировку были бы минимальными.
Пример расположения ячеек с исходными данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке
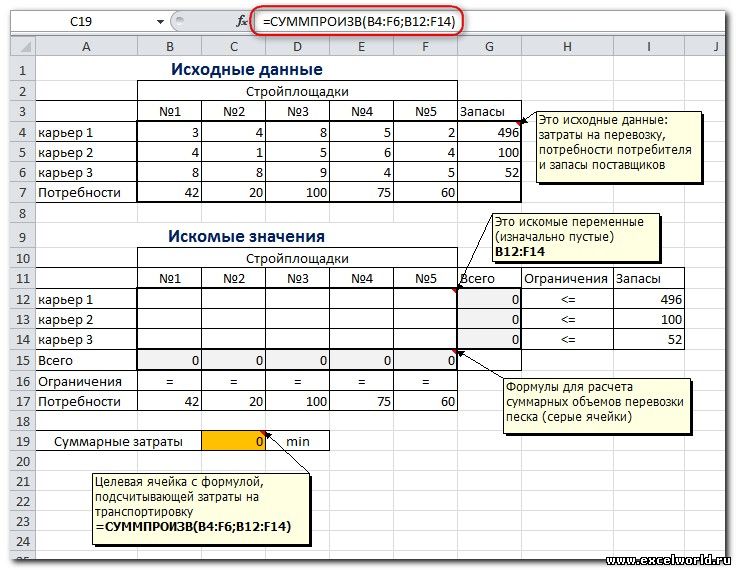
В серых ячейках формулы суммы по строкам и столбцам, а в целевой ячейке формула для подсчёта общих затрат на транспортировку .
Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)
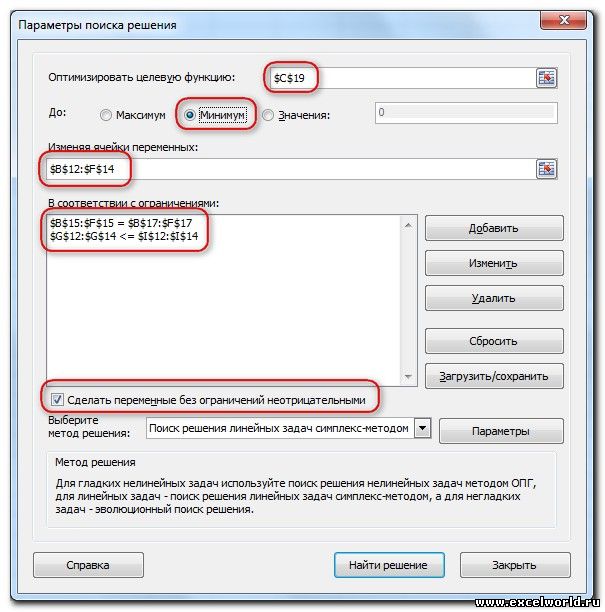
Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже
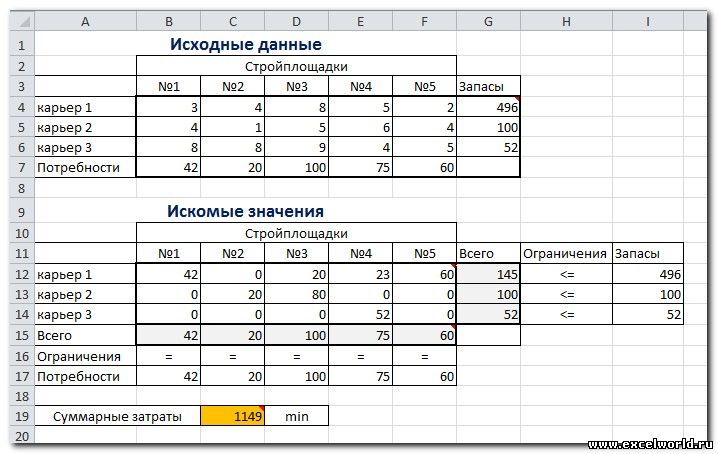
Иногда транспортные задачи усложняются с помощью дополнительных ограничений. Например, по каким-то причинам невозможно возить песок с карьера 2 на стройплощадку №3. Добавляем ещё одно ограничение $D$13=0. И после запуска Поиска решения получаем другой результат
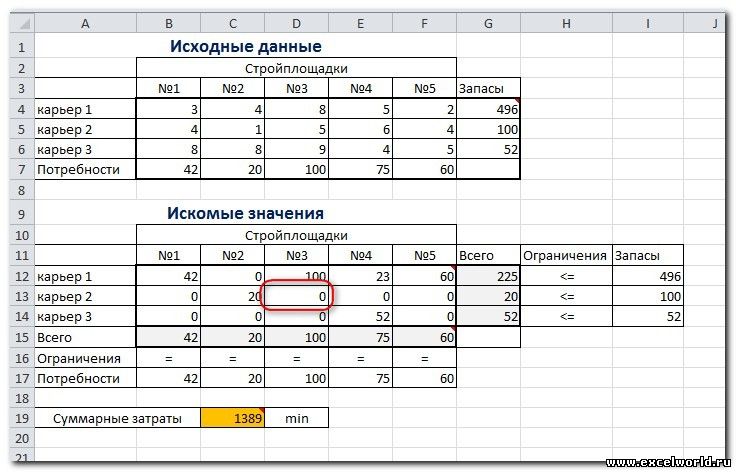
И последнее, на что следует обратить внимание, это выбор метода решения. Если задача достаточно сложная, то для достижения результата может потребоваться подобрать метод решения
Источник: www.excelworld.ru