Заданы координаты трех вершин треугольника (x1, y1), (x2, y2), (x3, y3). Найдите его периметр и площадь.
Для решения данной задачи необходимо вспомнить формулы длины прямой, заданной координатами, периметра и полупериметра треугольника, а также площади треугольника по трем сторонам:
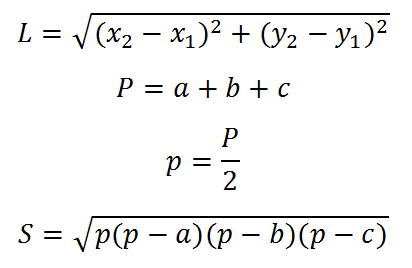
Формулы длины прямой по координатам, периметра, полупериметра и площади треугольника
Далее пишем простейшую программу:
program z_8; var x1, y1, x2, y2, x3, y3, P, p2, S, a, b, c: real; begin write(‘Координаты первой точки (через пробел)’); read(x1, y1); write(‘Координаты второй точки (через пробел)’); read(x2, y2); write(‘Координаты третьей точки (через пробел)’); read(x3, y3); a:=sqrt(sqr(x2-x1)+sqr(y2-y1)); b:=sqrt(sqr(x3-x2)+sqr(y3-y2)); c:=sqrt(sqr(x3-x1)+sqr(y3-y1)); P:=a+b+c; p2:=P/2; S:=sqrt(p2*(p2-a)*(p2-b)*(p2-c)); writeln(‘Периметр: ‘, P); writeln(‘Площадь: ‘, S); end.
Текст задачи:
Информатика. 10 класс. Базовый уровень. (Семакин И. Г., Хеннер Е. К., Шеина Т. Ю.)
Найти площадь прямоугольника, треугольника или круга. Решение задачи на Python
Работа 3.1, Уровень 2, Задача №8
Источник: easyinformatics.ru
Задача — Найти площади разных фигур — программирование на разных языках

Задача — Найти площади разных фигур
— программирование на Pascal, Си, Кумир, Basic-256, Python
В зависимости от выбора пользователя вычислить площадь круга, прямоугольника или треугольника. Для вычисления площади каждой фигуры должна быть написана отдельная функция.
Пусть программа может вычислять площади трех фигур: круга, прямоугольника и треугольника. Для вычисления каждой из них необходима отдельная функция. Пусть каждая из этих функций возвращает полученную площадь, а принимает параметры, необходимые для ее вычисления.
Для вычисления площади круга необходим радиус, для прямоугольника — длины двух сторон, для треугольника (если площадь вычисляется по формуле Герона) — длины трех сторон. Следовательно, функции будут различаться по количеству параметров.
Площадь круга вычисляется по формуле πr2.
Площадь прямоугольника является произведением двух его сторон.
Площадь треугольника по формуле Герона рассчитывается через полупериметр (p=(a+b+c)/2, где a, b и c — длины сторон треугольника) по формуле sqrt(p * (p-a) * (p-b) * (p-c)), где sqrt — квадратный корень.
В основной ветке программы должен происходить выбор, площадь какой фигуры необходимо вычислить. В зависимости от выбора будут запрашиваться необходимые данные (радиус или длины сторон) и передаваться в соответствующую функцию. Возвращаемое из функции значение будет выводиться на экран.
Нахождение длины окружности и площади круга на Паскаль
Pascal
var
choice: char;
a, x, y, z: real;
function circle(r: real): real;
begin
circle := pi * sqr(r);
end;
function rectangle(a, b: real): real;
begin
rectangle := a * b
end;
function triangle(a, b, c: real): real;
var x: real;
begin
x := (a + b + c) / 2;
triangle := sqrt(x * (x — a) * (x — b) * (x — c))
end;
begin
write(‘Круг(c), прямоугольник(r) или треугольник(t): ‘);
readln(choice);
case choice of
‘c’: begin
write(‘Радиус: ‘);
readln(x);
a := circle(x)
end;
‘r’: begin
write(‘Длина и ширина: ‘);
readln(x, y);
a := rectangle(x, y)
end;
‘t’: begin
write(‘Стороны: ‘);
readln(x, y, z);
a := triangle(x, y, z)
end
end;
writeln(‘Площадь: ‘, a:4:2);
end. Круг(c), прямоугольник(r) или треугольник(t): c
Радиус: 2
Площадь: 12.57
Круг(c), прямоугольник(r) или треугольник(t): r
Длина и ширина: 3.85 12.55
Площадь: 48.32
Круг(c), прямоугольник(r) или треугольник(t): t
Стороны: 3 4 6.5
Площадь: 4.17
В Паскале существует встроенная константа π (pi).
Язык Си
float circle(float);
float rectangle(float, float);
float triangle(float, float, float);
main() char ch;
float a,b,c;
printf(«Круг(c), прямоугольник(r) или треугольник(t): «);
scanf(«%c»,
switch (ch) case ‘c’:
printf(«Радиус: «);
scanf(«%f»,
printf(«Площадь круга %.2fn», circle(a));
break;
case ‘r’:
printf(«Длина и ширина: «);
scanf(«%f%f», b);
printf(«Площадь прямоугольника: %.2fn», rectangle(a,b));
break;
case ‘t’:
printf(«Стороны: «);
scanf(«%f%f%f», b,
printf(«Площадь треугольника: %.2fn», triangle(a,b,c));
break;
>
>
float circle(float r) return 3.14159 * r * r;
>
float rectangle(float x, float y) return x * y;
>
float triangle(float x, float y, float z) float p;
p = (x+y+z) / 2;
return sqrt(p * (p-x) * (p-y) * (p-z));
>
Компилировать с ключом -lm .
Python
def circle(r):
return math.pi * r**2
def rectangle(a, b):
return a*b
def triangle(a, b, c):
p = (a+b+c)/2
return math.sqrt(p * (p-a) * (p-b) * (p-c))
choice = input(«Круг(к), прямоугольник(п) или треугольник(т): «)
if choice == ‘к’:
rad = float(input(«Радиус: «))
print(«Площадь круга: %.2f» % circle(rad))
elif choice == ‘п’:
l = float(input(«Длина: «))
w = float(input(«Ширина: «))
print(«Площадь прямоугольника: %.2f» % rectangle(l,w))
elif choice == ‘т’:
AB = float(input(«Первая сторона: «))
BC = float(input(«Вторая сторона: «))
CA = float(input(«Третья сторона: «))
print(«Площадь треугольника: %.2f» % triangle(AB,BC,CA))
КуМир
алг площадь фигуры
нач
вещ а, б, в
сим фигура
вывод «Круг(к), прямоугольник(п), треугольник(т): »
ввод фигура
если фигура = «к» то
вывод «Радиус: »
ввод а
вывод «Площадь круга: «, круг(а)
иначе
если фигура = «п» то
вывод «Длина: »
ввод а
вывод «Ширина: »
ввод б
вывод «Площадь прямоугольника: «, прямоугольник(а,б)
иначе
если фигура = «т» то
вывод «Сторона 1: »
ввод а
вывод «Сторона 2: »
ввод б
вывод «Сторона 3: »
ввод в
вывод «Площадь треугольника: «, треугольник(а,б,в)
все
все
все
кон
алг вещ круг (вещ р)
нач
знач := 3.14 * р**2
кон
алг вещ прямоугольник (вещ д, вещ ш)
нач
знач := д * ш
кон
алг вещ треугольник (вещ ст1, вещ ст2, вещ ст3)
нач
вещ п
п := (ст1 + ст2 + ст3) / 2
знач := sqrt(п * (п — ст1) * (п — ст2) * (п — ст3))
кон
Basic-256
input «Круг (к), прямоугольник (п) или треугольник (т): «, ch$
if ch$ = «к» then
gosub circ
else
if ch$ = «п» then
gosub rectangle
else
if ch$ = «т» then
gosub triangle
endif
endif
endif
end
circ:
input «Радиус: «, r
print «Площадь круга: » + (pi * r^2)
return
rectangle:
input «Длина: «, a
input «Ширина: «, b
print «Площадь прямоугольника: » + (a*b)
return
triangle:
input «Первая сторона: «, a
input «Вторая сторона: «, b
input «Третья сторона: «, c
p = (a+b+c) / 2
s = sqrt(p * (p-a) * (p-b) * (p-c))
print «Площадь треугольника: » + s
return
В функции ничего не передается и ничего из них не возвращается.
Источник: ars-games.ru
Подготовка к олимпиадам по информатике
Может быть задан:
1. Длинами сторон a , b , c .
2. Координатами вершин (х А,уА), (х B ,у B ), (х C ,у C ) .
Длину стороны треугольника можно найти как расстояние между двумя точками.
Расстояние между точками М1(х1,у1) и М2(х2,у2) на плоскости определяется по формуле:

Признак существования треугольника: сумма двух сторон треугольника больше третьей стороны:
c a + b , a где a, b, c – стороны треугольника.
Виды треугольников
1. По сторонам:
равносторонний ( a = b = c );
равнобедренный( равны две стороны треугольника);
разносторонний (стороны не равны).
2. По углам:
Прямоугольный (с 2 = a 2 + b 2 , c — большая сторона треугольника);
Тупоугольный (с 2 > a 2 + b 2 , если c — большая сторона треугольника);
Остроугольный (с 2 a 2 + b 2 , c — большая сторона треугольника).
Площадь треугольника
1. Формула Герона

, a , b , c – стороны треугольника, p =( a + b + c )/2 – полупериметр.
Примечание: Такой метод вычисления площади имеет один существенный недостаток: необходимо выполнение операции нахождения квад ратного корня из числа. При выполнении этой операции часто происходит потеря точ ности, что может привести к получению не совсем точного результата.
2. Для прямоугольного треугольника:
S =( ab )/2, a , b — катеты (стороны при прямом угле).
3. По стороне треугольника и проведенной к ней высоте:
S=ah/2, где a — сторона треугольника, h — высота, проведенная к этой стороне.
4. По двум сторонам и углу между ними:
S=0,5ab*sin A, где a, b — стороны треугольника и А — угол между ними.
Примечание: При вычислении синуса угла происходит потеря точности.
Задание 1. Даны три числа а, b , с. Определить, существует ли треугольник с такими длинами сторон. Если треугольник существует определить его вид и площадь.
Формат ввода:
В первой строке три числа
Формат вывода:
В первой строке ответ — существует или не существует
Во второй строке — вид треугольника
В третьей строке — площадь треугольника
Тесты Посмотреть решение
Задание 2. Дан треугольник с вершинами (X1, Y1); (X2, Y2); (X3, Y3). Найти периметр треугольника.
Формат ввода:
В первой строке два числа — координата (х1;у1)
Во второй строке два числа — координата (х2;у2)
В третьей строке два числа — координата (х3;у3)
Формат вывода:
В первой строке ответ — периметр треугольника
Четырехугольник
Признак существования четырехугольника : длина одной из его сторон меньше, чем сумма длин трех остальных сторон: d a + b + c , a
Прямоугольник

Площадь прямоугольника
1. По координатам противоположных вершин
Будем рассматривать прямоугольники, стороны которых параллельны осям координат. В этом случае прямоугольник может быть определен одной из своих диагоналей. Это значит, что пара точек на плоскости с координатами (х1; y1) и (х2; y2), соответствующая концам диагонали, однозначно определяет расположение и размер прямоугольника.

Площадь прямоугольника вычисляется по формуле:
где |х2— x1| —длина проекции прямоугольника на ось Ох (длина стороны, параллельной оси Ox), a |y2 — y1| — длина проекции прямоугольника на ось Оу (длина стороны, параллельной оси Оу).
2. По двум сторонам
S=a*b, a, b — стороны прямоугольника, (S=a* a – площадь квадрата, а – сторона квадрата)
Трапеция
Площадь трапеции
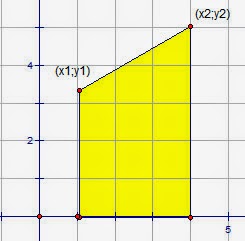
1. По координатам боковой стороны
Будем рассматривать трапеции, основания которых параллельны оси Оу, одна из боковых сторон лежит на оси Ох, а другая расположена выше оси Ох.
В этом случае трапеция может быть определена парой точек (х1; y1) и (х2; y2), соответствующих вершинам трапеции, не лежащим на оси Ох.
Площадь трапеции находим по формуле

где |х2-х1| – высота трапеции, а у2 и у1 – длины ее оснований.
2. По основаниям и высоте
S=h* (a+b)/2, где a, b – основания трапеции, h — высота трапеции.
Задание 3. Даны четыре числа а, b, с, d. Определить, существует ли четырехугольник с такими длинами сторон. Если существует, найти его периметр.
Формат ввода:
В первой строке четыре числа — стороны четырехугольника
Формат вывода:
В первой строке ответ — существует или не существует
Во второй строке — периметр
Тесты Посмотреть решение
Задание 4. Дан прямоугольник, заданный двумя противоположными вершинами (X1, Y1); (X2, Y2) и точка (X, Y). Определить площадь прямоугольника. Cтороны прямоугольника параллельны осям координат. Определить положение точки с координатами (Х, Y) — внутри или снаружи прямоугольника.
Формат ввода:
В первой строке два числа — координата (х1;у1)
Во второй строке два числа — координата (х2;у2)
В третьей строке два числа — координата (х;у)
Формат вывода:
В первой строке ответ — площадь
Во второй строке — положение точки
Экспериментальный раздел
1. Прямоугольник задан координатами своих вершин: (х1;у1), (х2;у2), (х3;у3), (х4;у4). Определить площадь прямоугольника.
2. Трапеция задана координатами своих вершин: (х1;у1), (х2;у2), (х3;у3), (х4;у4). Определить площадь трапеции.
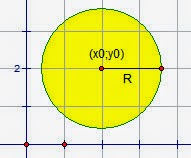
Площадь круга
S=Пи*R 2 , R- радиус окружности, Пи = 3,14 – постоянная величина.
Уравнение окружности
R 2 =(x-x0) 2 +(y-y0) 2 — центр (х0;у0) и радиус R
х 2 +у 2 =R 2 – уравнение окружности с центром в начале координат
Длина окружности
C= 2*Пи*R
Задание 5. Найти взаимное расположение окружности радиуса R с центром в точке (х0; у0) и точки А с координатами (x1;y1).
Формат ввода:
В первой строке два числа — координаты (х0;у0)
Во второй строке два числа — координаты (х1;у1)
В третьей строке число — радиус окружности
Формат вывода:
В первой строке ответ — внутри, снаружи или на окружности
Задание 6. Определить количество точек с целочисленными координатами, лежащих внутри окружности радиуса R с центром в точке (х0; у0).
Формат ввода:
В первой строке два числа — координаты (х0;у0)
Во второй строке число — радиус окружности
Формат вывода:
В первой строке ответ — количество точек с целочисленными координатами, которые лежат внутри окружности
Экспериментальный раздел
1. Найти координаты точек пересечения двух окружностей радиусов R1 и R2 с центрами в точках (х1, у1) и (x2,y2) соответственно.
Формат ввода:
В первой строке два числа — координаты (х1;у1)
Во второй строке два числа — координаты (х2;у2)
В третьей строке число — R1
В четвертой строке число — R2
Формат вывода:
В первой строке ответ — пересекаются или не пересекаются
Во второй строке — координаты точек пересечения
Задания для самостоятельного решения
1. Даны три точки с координатами (х1; у1), (х2, у2), (х3, у3), которые являются вершинами некоторого прямоугольника. Найти координаты четвертой вершины.
2. Даны координаты вершин четырехугольника (х1, у1), (х2; у2), (х3; у3), (х4; у4). Определить, является ли четырехугольник: а) ромбом; б) квадратом; в) прямоугольник.
3. Даны координаты двух вершин (x1;y1) и (x2,y2) некоторого квадрата. Найти возможные координаты других его вершин.
4. Найти взаимное расположение двух окружностей радиуса R1, и R2 с центрами в точках (х1, у1,) и (х2; у2) соответственно.
Источник: pinskolimp.blogspot.com