Программа нахождение нулей функции

Поставленную задачу в Matlab решает функция fzero.

b=fzero(‘fun’,x) возвращает уточненное значение b, при котором достигается нуль функции fun при начальном значении аргумента x. Возвращенное значение близко к точке, где функция меняет знак, или равно NaN, если такая точка не найдена. Функция fun должна оформляться в виде m-файла-функции y=fun(x).

b=fzero(‘fun’,x) возвращает значение, при котором функция равна нулю. Интервал поиска задается с помощью вектора x=[x1,x2] длиной 2 такого, что fun(x1) и fun(x2) имеют разные знаки. Если знаки не разные, то выдается сообщение об ошибке.

b=fzero(‘fun’,x,tol) возвращает значение, при котором функция равна нулю, с заданной относительной погрешностью tol.

b=fzero(‘fun’,x,tol,trace) выдает на экран информацию по каждой итерации, когда tol не нулевой.

b=fzero(‘fun’,x,tol,trace,p1,p2,…) предусматривает дополнительные аргументы, передаваемые в функцию y=fun(x,p1,p2,…). Чтобы использовать значения tol или trace по умолчанию, необходимо ввести пустые матрицы, например, b=fzero(‘fun’,x,[],[],p1,p2,…).

Нули функции / Где они? / как их найти / Все про функции (урок 6)

В функции fzero ноль рассматривается как точка, где график функции fun пересекает ось x, а не касается ее. В зависимости от формы задания функции fzero реализуются следующие методы поиска нуля функции: деления отрезка пополам, секущих, обратного квадратичного интерполирования.

4. Порядок выполнения работы

1. Написать m-файлы-сценаии для нахождения нуля функции методами деления отрезка пополам и Ньютона (4.7) с заданным числом итераций. Функцию взять согласно номеру компьютера. Предусмотреть построение графика функции на интервале поиска корня (на отрезке x[0.1,4]).

2. На отрезке x[1,2] найти решение нелинейного уравнения

1. методом деления отрезка пополам, число итераций 15;
2. методом Ньютона, число итераций 15.

3. Сравнить результаты поиска различными методами по погрешности решения. Вычислить невязку решения.

4. Выполнить поиск нуля заданной функции с помощью функции Matlab fzero. Сравнить полученные результаты.

5. Содержание отчета

1. Цель работы. Задание.
2. Описание метода решения, краткие сведения из теории (формулы, алгоритм и т.п.).
3. Программа (распечатка), ее описание.
4. Сравнение результатов расчета.
5. Краткие выводы по работе.

6. Задания лабораторной работы

7. y=sin(sin(x 2 ))-1/2;

11. y=(ln(x)+x) sin(x 2 )+1;

13. y=x-x sin(x 2 )-1;

15. y=exp(-sin(x 2 ))-1;

17. y=sin(x exp(x)/2)-x+1;

19. y=x 2 exp(-x 2 )-sin(x)+3/4;

21. y=cos(x 2 )-ln(x)+1;

23. y=sin(3x 2 /2)-ln(x);

25. y=sin(x 2 )-exp(-x/2);

27. y=2 exp(-cos(x 2 )-1/2)-ln(x)-1;

29. y=(ln(x)+x) cos(x 2 )+1/3;

10. y=sin(3x 2 /2)-x+2;

12. y=cos(x 2 )-exp(-x/2)+1;

14. y=cos(log(x)-cos(x 2 ))-1/3;

16. y=cos(cos(x 2 ))-5/6;

18. y=x cos(2x)+exp(-x)+1;

20. y=sin(ln(x)+2x 2 )+x 2 -2;

22. y=sin(cos(2x 2 ))+x 2 -2;

Как найти нули функции? #shorts

24. y=x 2 cos(2ln(x 2 )+1)+x;

26. y=x 3 cos(x 2 )-x 2 cos(x)+1;

28. y=ln(x)+cos(x 2 )sin(x);

30. y=ln(cos(x)+1)+cos(2x 2 );

Источник: studfile.net

Использование математического пакета MATLAB для исследования функций

Для решения уравнений вида f (x) = 0 (то есть для нахождения нулей функции) предназначена встроенная функция MATLAB fzero, которая находит приближённое значение корня уравнения по заданному начальному приближению.

Самый простой способ обращения к этой функции выглядит так:

где х0 – это начальное приближение к корню; fun – функция, корень которой вычисляется; а х – полученное приближение значения корня.

Аргумент х0 может быть задан либо в виде скалярного значения, вблизи которого возможно наличие корня, либо в виде вектора из двух значений [m n] (причем n > m), элементы которого представляют собой интервал, на границах которого функция fun имеет разные знаки (что означает наличие хотя бы одного корня на этом промежутке).

Рассмотрим случай задания аргумента fun в виде файл-функции.

В файл-функциях описываются функции, определяемые пользователем. Такие функции используются при решении многих задач, основанных на численных методах. Файл-функции представляют собой разновидность m-файлов. Вообще, в MATLAB существуют два типа m-файлов: файл-программы и файл-функции.

Допустим, требуется найти нули функции f (x) = х 2 sin(x) Сначала нужно создать файл функцию. Для этого выполните следующие действия:

1. В главном окне MATLAB выберите команду File Þ New Þ m-file (ФайлÞНовый Þm-файл), чтобы вызвать редактор m-файлов системы MATLAB.

2. Наберите в редакторе m-файлов две строки кода, изображённые на рис. 3.22.

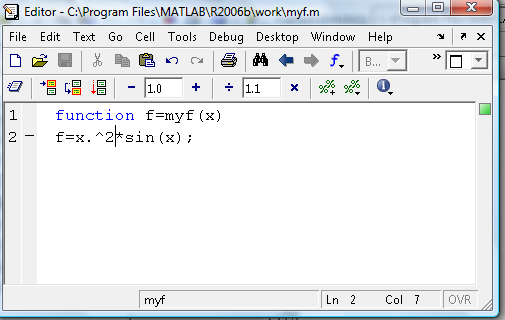
Рис. 3.22. Окно редактора кода с текстом файл-функции

Первая строка – это заголовок функции, где задаётся имя функции (в нашем примере myf) и список входных и выходных параметров (в данном случае имеется один входной (х) и один выходной (f) параметр). Во второй строке задаётся тело функции – выражение, вычисляющее значение функции. Обратите внимание, что при вводе функции использованы операторы поэлементного возведения в степень и поэлементного умножения, чтобы функцию можно было использовать и при работе с массивами. Кроме того, во избежание вывода на экран лишней информации, в конце второй строки кода поставлена точка с запятой.

3. Сохраните файл в текущем рабочем каталоге. Для этого в окне редактора m-файлов выберите команду FileÞSave as (ФайлÞСохранить как). В раскрывшемся диалоговом окне не изменяйте содержимое полей File name (Имя файла) Files of type (Тип файла), в которых автоматически отобразятся требуемые имя и тип файл-функции. Имя m-файла обязательно должно совпадать с именем функции (в данном случае для функции выбрано имя myf).

Перед тем как искать нули функции с помощью функции fzero, построим график заданной функции.

Файл-функции можно применять в качестве аргументов других функций, поэтому для построения графика вместо функции plot воспользуемся функцией fplot, работать с которой намного проще. В первом аргументе функции fplot достаточно задать имя файл-функции, график которой требуется построить, а во втором – вектор-строку из двух элементов, определяющих границы отрезка, на котором нужно построить график.

Чтобы построить график нашей функции на отрезке [0, 10], ввёдем следующие команды (командой grid on укажем программе отобразить сетку на графике):

» fplot(‘myf’,[0 10]); grid on.

Преимуществом использования функции fplot для построения графиков является то, что она автоматически подбирает шаг аргумента, что позволяет более точно описать поведение функции.

Как следует из графика (рис. 3.23), на отрезке [0, 10] функция имеет четыре корня. Один из корней равен нулю, а три других располагаются около значений х = 3, х = 6 и x = 9.

Рис. 3.23. График функции f (x) = х 2 sin x

С помощью функции fzero найдём более точные значения этих корней:

Вместо имени файл-функции в первом аргументе функции fzero можно явно задать исследуемую функцию, введя соответствующее ей выражение в одинарных кавычках. Результат вычислений будет таким же:

Если функцию fzero вызвать с двумя выходными параметрами, то можно получить значение функции в найденной точке:

Как видно по значению функции, точность вычисления корня с помощью функции fzero довольно высока.

Например, первым аргументом функции fzero может быть и встроенная функция системы MATLAB:

Для решения систем нелинейных уравнений вида f (х) = 0 (где х – вектор или матрица неизвестных, а f – функция, значением которой является вектор или матрица) в MATLAB предназначена функция fsolve. Данная функция относится к функциям пакета Toolbox Optimization.

Минимизация функций

Вычисление локального минимума функции одной переменной на заданном отрезке в MATLAB выполняет функция fminbnd, синтаксис которой аналогичен синтаксису функции fzero.

При её использовании также рекомендуется предварительно построить график исследуемой функции, чтобы можно было точнее определить отрезки поиска минимумов.

Самый простой способ обращения к функции fminbnd имеет вид:

где значения х1 и х2 задают границы отрезка поиска минимума; fun – функция, локальный минимум которой вычисляется (задаётся как имя файл-функции в одинарных кавычках либо как формула с одной независимой переменной, заключённая в одинарные кавычки); а х – вычисленное значение, при котором достигается минимум.

Найдём локальный минимум для рассмотренной в предыдущем разделе функции f (x) = x 2 sin x на отрезке [2, 8]. Для этого введем в командную строку следующие команды:

Таким образом, локальный минимум на отрезке [2, 8] достигается при х = 5,0870.

Чтобы узнать значение исследуемой функции в точке минимума, нужно вызвать функцию fminbnd с двумя выходными аргументами:

Для нахождения локального максимума в MATLAB не предусмотрено специальной функции. Однако найти локальный максимум требуемой функции, очевидно, можно путём вычисления локального минимума для функции, имеющей обратный знак.

Интегрирование функций

В системе MATLAB реализованы различные методы численного интегрирования функций.

Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.

Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычис­лить, когда этот.

Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Источник: zdamsam.ru

Иллюстрированный самоучитель по MatLab

Примечание
Подфункциями понимаются как встроенные функции, например sin(x) или ехр(х),так и функции пользователя, например f(x), задаваемые как т-файлы-функции.

Численные значения таких функций, заданных дескрипторами, вычисляются с помощью функции feval:

> > feval(fe. 1.0 )

Довольно часто возникает задача решения нелинейного уравнения вида f(x) = 0 или /, (г) =/ 2 (дг). Последнее, однако, можно свести к виду f(x) =f 1 (х) – f 2 (х) = 0. Таким образом, данная задача сводится к нахождению значений аргумента х функции f(x) одной переменной, при котором значение функции равно нулю. Соответствующая функция MATLAB, решающая данную задачу, приведена ниже:

fzero(fun,x,[ ],[ ],P1)

Для функции fzero ноль рассматривается как точка, где график функции fun пересекает ось х, а не касается ее. В зависимости от формы задания функции fzero реализуются следующие хорошо известные численные методы поиска нуля функции: деления отрезка пополам, секущей и обратной квадратичной интерполяции. Приведенный ниже пример показывает приближенное вычисление р/2 из решения уравнения cos(x)=0 с представлением косинуса дескриптором:

В более сложных случаях настоятельно рекомендуется строить график функции f(x) для приближенного определения корней и интервалов, в пределах которых они находятся. Ниже дан пример такого рода (следующий листинг представляет собой содержимое m-файла fun1.m):

%Функция, корни которой ищутся
function f = funl(x)
f = 0.25 * x + sin(x) — 1 ;
> > x = 0 : 0.1 : 10 ;
> > plot(x,funl(x));grid on ;

Из рисунка нетрудно заметить, что значения корней заключены в интервалах [0.5 1], [2 3] и [5 6]. Найдем их, используя функцию fzero:

Обратите внимание на то, что корень х3 найден двумя способами и что его значения в третьем знаке после десятичной точки отличаются в пределах заданной погрешности tol =0.001. К сожалению, сразу найти все корни функция fzero не в состоянии. Решим эту же систему при помощи функции fsolve из пакета Optimization Toolbox, которая решает систему нелинейных уравнений вида f(x)=0 методом наименьших квадратов, ищет не только точки пересечения, но и точки касания, fsolve имеет почти те же параметры (дополнительный параметр – задание якобиана) и почти ту же запись, что и функция lsqnonneg, подробно рассмотренная ранее. Пример:

Columns 1 through 7
0.8905 0.8905 2.8500 2.8500 2.8500 5.8128 5.8128
Columns 8 through 11
5.8128 2.8500 2.8500 10.7429

Для решения систем нелинейных уравнений следует также использовать функцию solve из пакета Symbolic Math Toolbox. Эта функция способна выдавать результат в символьной форме, а если такого нет, то она позволяет получить решение в численном виде. Пример:

> > solve( 0.25 * x + sin(x) — 1 )
. 89048708074438001001103173059554

[Пакеты расширения Symbolic Math ToolBox и Extended Symbolic Math Toolbox MATLAB 6.0 используют ядро Maple V Release 5 [30-35] и являются поэтому исключением: они пока не поддерживают новую нотацию с использованием дескрипторов функций. – Примеч. ред.]

РЕКЛАМА

СОДЕРЖАНИЕ

• Введение
• Знакомство с матричной лабораторией MATLAB
• Установка системы и первые навыки работы
• Основы графической визуализации вычислений
• Работа со справкой и примерами
• Пользовательский интерфейс MATLAB
• Обычная графика MATLAB
• Специальная графика
• Операторы и функции
• Специальные математические функции
• Операции с векторами и матрицами
• Матричные операции линейной алгебры
• Функции разреженных матриц
• Многомерные массивы
• Массивы структур
• Массивы ячеек
• Численные методы

• Элементарные средства решения СЛУ
• Функции для решения систем линейных уравнений с ограничениями
• Решение СЛУ с разреженными матрицами. Точное решение, метод наименьших квадратов и сопряженных градиентов.
• Двунаправленный метод сопряженных градиентов. Устойчивый двунаправленный метод.
• Метод сопряженных градиентов
• Квадратичный метод сопряженных градиентов. Метод минимизации обобщенной невязки. Квазиминимизация невязки.
• Вычисление нулей функции одной переменной
• Минимизация функции одной переменной
• Минимизация функции нескольких переменных
• Аппроксимация производных. Аппроксимация Лапласиана.
• Апроксимация производных конечными разностями
• Вычисление градиента функции
• Численное интегрирование. Метод трапеций.
• Численное интегрирование методом квадратур
• Работа с полиномами. Умножение и деление полиномов.
• Вычисление полиномов. Вычисление производной полинома.
• Решение полиномиальных матричных уравнений. Разложение на простые дроби.
• Решение обыкновенных дифференциальных уравнений. Решатели ОДУ.
• Использование решателей систем ОДУ
• Описание системы ОДУ
• Дескрипторная поддержка параметров решателя
• Пакет Partial Differential Equations Toolbox

Если Вы заметили ошибку, выделите, пожалуйста, необходимый текст и нажмите CTRL + Enter, чтобы сообщить об этом редактору.

Источник: samoychiteli.ru