Пусть функция f(x) определена на некотором промежутке, x — точка этого промежутка и число h ≠ 0 такое, что x + h так же принадлежит данному промежутку. Тогда предел разностного отношения $$ quad $$ при $$ quad h rightarrow 0$$ (если этот предел существует) называется производной функции f(x) в точке x и обозначается f'(x).
Таким образом, $$ f'(x) = lim_ $$ Отметим, что в формуле производной число h, где h≠0, может быть как положительным, так и отрицательным, при этом число x + h должно принадлежать промежутку на котором определена функция f(x). Если функция f(x) имеет производную в точке x, то эта функция называется дифференциируемой в этой точке. Если функция f(x) имеет производную в каждой точке некоторого промежутка, то говорят, что эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием. Геометрический смысл производной состоит в том, что значение производной функции f(x) в точке x равно угловому коэффициенту касательной к графику функции в точке (x; f(x)).
Математика Без Ху%!ни. Производная сложной функции.
Примеры решений
- Найдите производную функции y=5x-6
Посмотреть решение
Решение: Для поиска производной воспользуемся производной суммы. $$ y’=(5x-6)’=(5x)’+(-6)’ $$ с учетом того, что производная от постоянной равна нулю, а производная от функции $$y=Cx=C$$, получим: $$ y’=(5x)’+(-6)’=5 $$ Ответ: $$ y’= 5 $$
Решение: $$ y’= left(4x^3 — frac> right)’ $$ $$ y’=(5x-6)’=(5x)’+(-6)’ $$ Для определения производства воспользуемся правилом определения суммы функций: $$ y’ = (4x^3)’ — left( frac right)’ + (cos(x))’ $$ Найдем каждую из производных по отдельности: Сначала используем производную степенной функции: $$ (4x^3)’ = 12x^2 ;$$ $$ left( frac<sqrt> right)’ = 2 cdot frac<(2sqrt)> = frac<sqrt>; $$ Затем производную тригонометрической функции cos: $$ (cos(x))’=-sin(x) $$ Получим: $$ y’ = 12x^2 — frac<sqrt> — sin(x) $$. Ответ: $$ y’ = 12x^2 — frac<sqrt> — sin(x) $$
Решение: Воспользуемся правилом для нахождения производной произведения функций $$(vu)’=v’u+uv’$$ : $$ y’ = (x^2)’ cdot arctg(x)+(arctg(x))’ cdot x^2 = 2x cdot arctg(x) + frac = 2x cdot arctg(x) + frac $$ Ответ: $$ 2x cdot arctg(x) + frac $$
Решение: $$ y = frac — frac + frac = 2x^2 — 3x + frac $$ $$ y’ = (2x^2 — 3x + frac)’ $$ $$ y’ = (2x^2)’ — (3x)’ + (frac)’ $$ $$ y’ = 4x-3- frac $$ Ответ: $$ y’ = 4x-3- frac $$
Решение: Данная функция является сложной, поэтому, сначала берем производную от внешней функции, и умножаем на производную от внутренней функции: $$ y’ = (sin(12x-5))’ $$ $$ y’ = sin'(12x-5) cdot (12x-5)’ $$ $$ y’ = cos(12x-5) cdot 12 = 12 cos(12x-5) $$ Ответ: $$ y’ = cos(12x-5) cdot 12 = 12 cos(12x-5) $$
Решение: Данная функция является сложной, поэтому, сначала берем производную от внешней функции, и умножаем на производную от внутренней функции: $$ y’=(3x^3 + 5x^2 — 11x + 6)’ = (3x^3)’ + (5x^2)’ — (11x)’ + (6)’ ; $$ $$ y’ = 9x^2 + 10x — 11 $$ После этого из полученной функции берем еще одну производную: $$ y»= ( 3x^3 + 5x^2 — 11x + 6 )» = (9x^2 + 10x — 11)’ = (9x^2)’ + (10x)’ — (11)’; $$ $$ y» = 18x + 10 $$ Ответ: $$ y» = 18x + 10 $$
АЛГЕБРА С НУЛЯ — Что такое Производная?
Решение: Используем формулы для нахождения производной от косинуса и показательной функции: $$ y’ = (cos(x))’ — (3^x)’ $$ $$ y’ = -sin(x) — (3^x cdot ln3) $$ Ответ: $$ y’ = -sin(x) — (3^x cdot ln3) $$
Решение: Имеем сложную функцию, где вложенной функцией является arcsin x: $$ y’ = (frac< arcsin^2x >)’ = ( frac ) cdot ( arcsin x )$$ $$ y’ = ( frac ) cdot frac > $$ Ответ: $$ y’ = ( frac ) cdot frac > $$
Решение: Для того, чтобы найти решение, сначала определим производную $$y=x^2$$, а затем производную внутренней функции $$3x-5$$ и перемножим их: $$ y’ = (ln^2(3x-5))’ $$ $$ y’ = 2 cdot ln(3x-5) cdot (3x-5)’ $$ $$ y’ = 2 cdot ln(3x-5) cdot 3 $$ $$ y’ = 6 cdot ln(3x-5)$$ Ответ: $$ y’ = 6 cdot ln(3x-5)$$
Источник: algebra24.ru
Онлайн Вычислитель производных
Wolfram|Alpha отлично справляется с нахождением производных первого, второго или третьего порядка, значений производных в точке, а также с вычислением частных производных. Узнайте, что такое производные и как Wolfram|Alpha их находит.
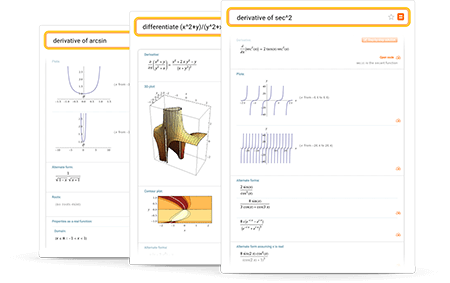
Рекомендации по составлению запросов
Вводите запросы на обычном английском языке. Использование скобок, в случае необходимости, позволяет избежать неоднозначностей в запросе. Вот некоторые примеры, иллюстрирующие запросы для вычисления производной.
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
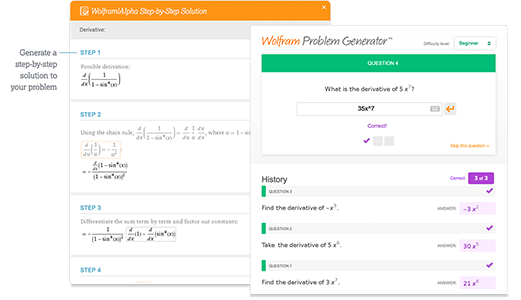
- Пошаговые решения »
- Wolfram Problem Generator »
Что такое производные?
Производная — это важный инструмент математического анализа, который отображает бесконечно малое изменение функции при изменении одной из её переменных.
Для функции , существует много способов обозначения производной относительно переменной . Наиболее распространенными являются обозначения и . Для обозначения кратной производной используют или . Кратные производные также называют производными старших порядков. Вторую производную также часто обозначают .
Производная в точке по определению равна . Этот предел не всегда определен, но когда он существует, о функции говорят, что она дифференцируема в точке . Говоря геометрически, дает тангенс угла наклона касательной к графику функции в точке .
Например, если , то и тогда мы можем найти вторую производную : . Производная является эффективным инструментом для решения многих прикладных задач. Например, она используется для определения локальных или глобальных экстремумов, точек перегиба, для решения задач оптимизации и описания траекторий движения объектов.
Каким образом Wolfram|Alpha находит производные
Wolfram|Alpha использует функцию D системы Mathematica, которая применяет таблицу тождеств, значительно превосходящую таблицы, приводимые в стандартных учебниках по математическому анализу. Она также использует ”хорошо известные” правила, такие как линейность производной, тождество Лейбница, правило дифференцирования степенной функции, правило дифференцирования сложной функции и т.п. Дополнительно, функция D использует ”менее известные” правила для вычисления производных широкого ряда специальных функций. Нахождение производных старших порядков использует некоторые правила, такие как общее тождество Лейбница, для увеличения быстродействия.
Источник: www.wolframalpha.com
Онлайн калькуляторы пределов, производных и их приложений
Данный раздел содержит онлайн калькуляторы для вычисления пределов и производных различных порядков для функций одной или многих переменных, заданных в обычной, неявной или параметрической форме. Для каждого калькулятора предусмотренно подробное решение.
Пределы, производные и их приложения 9
Вычисление пределов Калькулятор вычисляет предел выражения с описанием подробного хода решения на русском языке
Вычисление производной Калькулятор позволяет вычислить производную обычной функции с пошаговым решением на русском языке.
Вычисление производной функции заданной параметрически Калькулятор находит подробное решение производной функции, заданной параметрически.
Вычисление производной неявной функции Калькулятор находит производную функции, заданной неявным образом. Также доступно подробное решение на русском языке.
Вычисление частных производных Калькулятор находит частную производную функции нескольких переменных с описанием подробного хода решения на русском языке.
Калькулятор дифференциала функции NEW Калькулятор вычисляет дифференциалы различных порядов для функций одной или нескольких переменных.
Уравнение касательной к графику функции Калькулятор позволяет найти касательную к функции в заданной точке.
Уравнение нормали к графику функции Калькулятор находит нормаль к функции в заданной точке.
Калькулятор градиента функции NEW Калькулятор вычисляет градиент функции в общем виде или в заданной точке.