Описать структуру Точка на плоскости (определяется координатами x,y). Описать функции, которые рассчитывают расстояние от данной точки до начала координат, возвращает значение координат. Написать функцию, вычисляющую расстояние между двумя точками. Разработать программу, в которой вводятся координаты двух точек, определяется, какая из них ближе к началу координат и расстояние между ними.
Код к задаче: «Структура «Точка на плоскости»»
Листинг программы
#include #include typedef struct pt < int x; int y; >point_t; point_t makePoint(int x, int y); double getDistance(point_t pt); double getDistancePP(point_t pt1, point_t pt2); int main(void) < point_t point1 = makePoint(-7, -5); point_t point2 = makePoint(10, 3); double dist1 = getDistance(point1), dist2 = getDistance(point2); printf(«pt1 to start: %.2fn», dist1); printf(«pt2 to start: %.2fn», dist2); printf(«pt%d nearer to beginn», (dist1 < dist2) ? 1 : 2); printf(«pt1 to pt2 dist = %.2f», getDistancePP(point1, point2)); return 0; >point_t makePoint(int x, int y) < point_t tmp = ; return tmp; > double getDistance(point_t pt) < return sqrt(pow(pt.x, 2) + pow(pt.y, 2));; >double getDistancePP(point_t pt1, point_t pt2)
Кинематика точки в плоскости. Термех
Источник: studassistent.ru
Точка пересечения двух прямых на плоскости
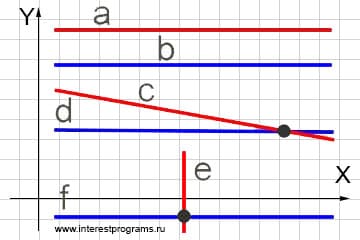
При разработке компьютерных игр, программ математических графиков, расчетов движения объектов и т.п. очень часто требуется найти точку пресечения прямых. Желательно предварительно на бумаге вывести и упростить формулы вычисления, а далее эти формулы проще будет перевести в программный код.
Прямые это бесконечные линии, поэтому на плоскости они всегда пересекаются. Если прямые не пересекаются значит они параллельны. Частные случаи поведения прямых на плоскости: прямые неопределенны, прямые параллельны, прямые совпадают, одна из прямых параллельна оси X или Y. Общие случаи «нормального» пересечения прямых и частные случаи учитываются в программном коде класса Intersections прикрепленного исходника.
Прямые пересекаются
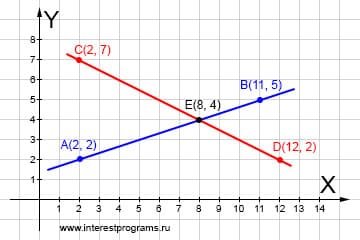
Даны две прямые AB и CD расположенные на одной плоскости. Они пересекаются и необходимо найти точку пересечения. За основу берем классическое уравнение прямой и подставляя данные получаем систему уравнений для двух прямых.
Точку пересечения можно найти, решая совместно уравнения прямых. Два уравнения — две неизвестных величины. Если количество уравнений больше или равно количеству неизвестных, то система решаема. Точка пересечения двух прямых это такая точка, которая принадлежит обеим прямым.
Математика без Ху%!ни. Уравнение плоскости.
Классическое уравнение прямой:
x — x1 y — y1 ——— = ——— (у.1) x2 — x1 y2 — y1
Запишем уравнение в одну строчку:
x(y2 — y1) + y(x1 — x2) — x1y2 + y1x2 = 0 (у.2)
Вычислим коэффициенты и свободные члены:
a = (y2 — y1) b = (x1 — x2) c = (-x1y2 + y1x2)
В итоге получаем уравнение прямой с коэффициентами:
ax + by + c = 0 (у.3)
Уравнение с линейными коэффициентами отличается от уравнения с угловым коэффициентом отсутствием операции деления. Минимум операций деления упрощает создание устойчивого программного кода.
Точка пересечения прямых
Координаты точки пересечения это числа которые являются решением для каждого из уравнений прямых. Решая систему из двух уравнений находим в какой точке пересекаются прямые AB и CD.
Подставляем известные данные:
AB x(5 — 2) + y(2 — 11) — 2*5 + 2*11 = 0 CD x(2 — 7) + y(2 — 12) — 2*2 + 7*12 = 0
Получаем два уравнения:
AB x — 3y + 4 = 0 CD x + 2y — 16 = 0
Решаем систему уравнений:
| | x = 3y — 4 => x = 3(-0.5x + 8) — 4 | y = -0.5x + 8 => y = -0.5(3y — 4) + 8 |
Найдено, прямые пересекаются в точке с координатами:
x = 8 y = 4
Прямые параллельны
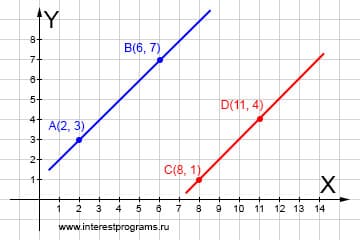
Если прямые параллельны и лежат друг от друга на расстоянии, то у них нет общих точек. Совместная система уравнений не имеет решений. Эти уравнения существуют как бы сами по себе. В точности как их параллельные прямые.
Две прямые могут полностью совпадать, в таком случае у них бесконечное количество общих точек. Совпадение прямых означает равность коэффициентов и свободных членов уравнений. Совпадающие прямые имеют идентичные уравнения.
Применяя формулу у.2 выведем уравнения прямых:
AB x(7 — 3) + y(2 — 6) — 2*7 + 3*6 = 0 CD x(4 — 1) + y(8 — 11) — 8*4 + 1*11 = 0
Получаем систему уравнений:
| | x — y — 25 = 0 => x — y = 25 | x — y — 7 = 0 => x — y = 7 | 25 ≠ 7
Итог: система уравнений параллельных прямых не имеет решений.
Уравнение в программный код
На бумаге всё славненько, надо также сделать и в программном коде. Но программы не разбираются в уравнениях, им подавай переменные, постоянные и функции. Программный код не терпит неопределенности, он требует точные данные. Очень желательно строить выражения без операций деления. Преобразуем в программный код уравнение с коэффициентами (у.3) описанное выше.
Для каждой прямой своё уравнение и переменные.
AB a1x + b1y + c1 = 0 CD a2x + b2y + c2 = 0
Точки определяющие прямые запишем в структуры Point. У каждой прямой две точки и они являются входными данными:
Point pABDot1; Point pABDot2; Point pCDDot1; Point pCDDot2;
Определяем коэффициенты и свободные члены уравнений. Записываем их в соответствующие переменные:
double a1 = pABDot2.Y — pABDot1.Y; double b1 = pABDot1.X — pABDot2.X; double c1 = -pABDot1.X * pABDot2.Y + pABDot1.Y * pABDot2.X; double a2 = pCDDot2.Y — pCDDot1.Y; double b2 = pCDDot1.X — pCDDot2.X; double c2 = -pCDDot1.X * pCDDot2.Y + pCDDot1.Y * pCDDot2.X;
Точка пересечения также будет храниться в структуре Point:
Point pCross;
Вывод результата
Упростим уравнение (у.3) для получения значений искомых координат. Чтобы освежить память сделаем это максимально подробно. Из одного уравнения выведем X, из другого Y:
a1x = -b1y — c1 => x = (-b1y — c1) / a1 => b2y = -a2x — c2 => y = (-a2x — c2) / b2 => x = ( -b1( (-a2x — c2) / b2) — c1 ) / a1 => y = ( -a2( (-b1y — c1) / a1) — c2) / b2 => x = ( (b1a2x + b1c2) / b2 — c1 ) / a1 => y = ( (a2b1y + a2c1) / a1 — c2) / b2 => x = ( (b1a2x + b1c2 — b2c1) / b2 ) / a1 => y = ( (a2b1y + a2c1 — a1c2) / a1) / b2 => x = ( b1a2x + b1c2 — b2c1) / b2 a1 => y = ( a2b1y + a2c1 — a1c2) / a1 b2 => xb2a1 — b1a2x = b1c2 — b2c1 => ya1b2 — a2b1y = a2c1 — a1c2 => x = (b1c2 — b2c1) / (b2a1 — b1a2) y = (a1c1 — a1c2) / (a1b2 — a1b1)
После упрощения и прихорашивания уравнений записываем искомые координаты X Y в объект pCross:
Point pCross; pCross.X = (b1 * c2 — b2 * c1) / (a1 * b2 — a2 * b1); pCross.Y = (a2 * c1 — a1 * c2) / (a1 * b2 — a2 * b1);
В выражениях присутствует деление. Но знаменатель только тогда и только тогда будет равен нулю, когда обе прямые будут параллельны или оси X или оси Y. В этом случае они не пересекаются или совпадают. Это отслеживаемые состояния в классе Intersections , и вывод информации заканчивается до выбрасывания исключения при делении на ноль.
Проверка параллельности и совпадения
В программном коде необходимо проверять прямые на параллельность. В этом случае система уравнений не имеет решений и возникнет исключение от попытки обработать нечисловые данные. Необходимым и достаточным условием параллельности двух прямых является пропорциональность их коэффициентов:
a1 / a2 = b1 / b2
Деление небезопасная операция для программного кода, при некоторых координатах знаменатель может оказаться нулем. И тогда программа остановится исключением, поскольку на ноль делить нельзя. Поэтому для программного кода исключим деление, преобразуя выражение в такой вид:
if ((a1 * b2 — a2 * b1) == 0) < // Прямые параллельны другу друг и не имеют точек пересечения . >
Если пропорциональны не только коэффициенты, но и свободные члены, то исследуемые прямые совпадают. У таких прямых идентичные уравнения. Прямые совпадают если:
a1 / a2 = b1 / b2 = c1 / c2
Данную ситуацию дополнительно отслеживаем в программном коде, исключая операцию деления:
if ((a1 * b2 — a2 * b1) == 0) < // Прямые параллельны другу друг и не имеют точек пересечения . if (a1 * b2 == b1 * a2 a1 * c2 == a2 * c1 b1 * c2 == c1 * b2) < // Прямые совпадают и имеют бесконечное количество решений . >>
Проверка на перпендикулярность
Перпендикулярность прямых это частный случай пересечения. Отслеживание этой ситуации иногда необходимо, например: в игре определить кратчайшую траекторию до длинной стены или определить отсутствие рикошета при выстреле. Необходимым и достаточным условием перпендикулярности прямых является данное соотношение коэффициентов:
a1a2 = -b1b2 или a1a2 + b1b2 = 0
В программном коде отследим эту ситуацию выражением:
if ((a1 * a2 + b1 * b2) == 0) < // Прямые перпендикулярны . >
Класс Intersections
Исходник представляет собой два класса: класс вычисления точки пересечения прямых и информационный класс выдающий множество дополнительных сведений о свойствах исследуемых прямых.
Краткий листинг исходника дающий представление о структуре классов:
// Вычисление точки пересечения прямых class Intersections < // Метод вычисления точки пересечения. private Point Cross(double a1, double b1, double c1, double a2, double b2, double c2) < Point pCross; pCross.X = (b1 * c2 — b2 * c1) / (a1 * b2 — a2 * b1); pCross.Y = (a2 * c1 — a1 * c2) / (a1 * b2 — a2 * b1); return pCross; >// Метод дающий полную информацию об исследуемых прямых и их пересечениях public bool LineLine(Point pABDot1, Point pABDot2, Point pCDDot1, Point pCDDot2, out Point pCross, out Info info) < // info = new Info(); double a1 = pABDot2.Y — pABDot1.Y; double b1 = pABDot1.X — pABDot2.X; double c1 = -pABDot1.X * pABDot2.Y + pABDot1.Y * pABDot2.X; double a2 = pCDDot2.Y — pCDDot1.Y; double b2 = pCDDot1.X — pCDDot2.X; double c2 = -pCDDot1.X * pCDDot2.Y + pCDDot1.Y * pCDDot2.X; . // Прямые параллельны if ((a1 * b2 — a2 * b1) == 0) < info.Id = 40; info.Message = «Прямые параллельны»; . if (a1 * b2 == b1 * a2 a1 * c2 == a2 * c1 b1 * c2 == c1 * b2) < info.Id = 43; info.Message = «Прямые совпадают»; >return false; > // ————— Прямые пересекаются ———————- // Точка пересечения прямых pCross = Cross(a1, b1, c1, a2, b2, c2); // Прямые перпендикулярны if ((a1 * a2 + b1 * b2) == 0) < info.Id = 50; info.Message = «Прямые перпендикулярны»; return true; >. return true; > // public bool LineLine(Point pABDot1. >// class Intersections // Идентификатор результата пересечения прямых // и пояснительное сообщение public class Info
Применение класса Intersections
Класс class Intersections легко встраивается в любой исходный код. Точки определяющие прямые являются входными данными. На выходе получаем результат пересечения, координаты точки пересечения. Для дальнейшей обработки результатов можно использовать идентификатор свойства пересечения и дополнительную текстовую информацию.
// Определяющие точки первой прямой Point pABDot1 = new Point(X1, Y1); Point pABDot2 = new Point(X2, Y2); // Определяющие точки второй прямой Point pCDDot1 = new Point(X1, Y1); Point pCDDot2 = new Point(X2, Y2); // Вычисляем точку пересечения прямых Intersections intersections = new Intersections(); Point pCross; Info info; bool res = intersections.LineLine(pABDot1, pABDot2, pCDDot1, pCDDot2, out pCross, out info); // Вывод информации о свойстве пересечения или непересечения crossInfo.Content = info.Message; if (res == true) < // Прямые пересекаются, // получены координаты точки пересечения. // Объект перемещается в точку пересечения. Obj.MoveTo(pCross.X, pCross.Y); . >else < // Пересечения прямых нет . >
Прикрепленный файл
Прикрепленный файл архива содержит исходник классов Intersections, Info и программу демонстрирующую работу класса Intersections в режиме вычисления точки пересечения прямых на плоскости. Исходный код написан на языке C#, но его легко можно преобразовать в код на другом языке программирования. Для работы демонстрационной программы необходима установка платформы .NET Core 3.1.
Источник: www.interestprograms.ru
Попадание точки в область (С++)
Задача: Ввести с клавиатуры координаты точки (x, y). Определить попала ли точка в заштрихованную область. 
Решение: Различные случаи (виды областей) и подходы к определению попадания в них точки рассмотрены в отдельной статье.
В данном случае алгоритм следующий: Если точка находится за пределами круга радиусом 2 — то выводим нет. Для проверки этого факта надо определить расстояние между точкой и центром и сравнить с радиусом.
Для вычисления расстояния между точками используется теорема Пифагора: Для проверки принадлежности ромбу можно исопльзовать тот факт, что линия между точками (0,1) и (1,0) образована такими точками, что сумму координат x+y у них равна единице. Если эта сумма меньше единицы — то тчка принадлежит треугольнику (0,1), (1, 0), (0, 0) . Однако, ромб состоит из 4 треугольников. Для проверки можно переместить точку (симметрично относительно нуля) в первую честверть координатной плоскости. Для этого достаточно вычислить модуль обоих координат. Блок-схема: 
На блок схеме используется символ перехода (круг), который можно использовать в рамках одного листа. Исходный код соответствующей программы:
#include #include using namespace std; int main() < double x, y; cout > x; cout > y; double d = sqrt(x*x + y*y); if (d > 2) < // за «бубликом» cout if (d > 1) < // на «бублике» if (x >= 0) < // правая часть координатной плоскости cout else < // левая cout return 0; > // внутри «бублика», переношусь в I четверть: x = abs(x); y = abs(y); if (x+y < 1) < // внутри ромба cout else < cout >
Для вычисления корня квадратного и модуля числа исопльзуются функции sqrt и abs , определнные в модулей cmath .
Просмотр 0 веток ответов
- Для ответа в этой теме необходимо авторизоваться.
Наша группа ВКонтакте.
-
Поиск пути в лабиринте (C++) опубликовано Васильев Владимир Сергеевич
1 неделя, 5 дней назад
2 недели, 2 дня назад
1 месяц назад
1 месяц, 2 недели назад
1 месяц, 2 недели назад
Источник: pro-prof.com