В этом разделе сайта progmatem.ru для рисования различных геометрических фигур в Паскале нам нам понадобится среда PascalABC.Net или PascalABC. Будут также привены рабочие программы в средах Turbo Pascal и Free Pascal. Вообще Паскаль хорош тем, что позволяет не только писать простые и/или сложные консольные приложения, но и работать с формами (как в Delphi), а также создавать графические приложения с помощью подключаемого модуля GraphABC (аналог модуля graph в Turbo Pascal, Free Pascal). Ведь для того и создавалась среда PascalABC.Net – как учебное пособие при переходе на Delphi – более совершенную версию Object Pascal.
При работе с графическим окном нужно учитывать две особенности. Во-первых, начало координат – точка (0, 0) – находится не где-то посредине окна, а в левом верхнем углу. Вторая особенность связана с первой: положительное направление оси OY показывает не вверх, а вниз (OX направлена вправо).
Как мы видим, система координат в графическом окне Pascal отлична от той, к которой мы привыкли в математике – т.н. правой системе координат, в которой ось OX направлена вправо, ось OY – вверх, а начало координат, как правило, всегда стоит где-то посредине окна. И к этой особенности надо привыкать.
Алгоритмы и исполнители. Чертежник. Процедуры. Pascal ABC.
Но что делать, если требуется нарисовать геометрическую фигуру или график функции в «нормальной», привычной для нас системе координат? Надо выполнить преобразование системы координат таким образом, чтобы точка (0, 0) находилась посредине окна (в любой нужной точке), а ось OY была направлена вверх. Стандартное преобразование в прямоугольной правой системе координат выглядит следующим образом:
Здесь x 0 и y 0 – координаты точки, в которую мы хотим перенести начало координат новой системы, x и y – координаты точки в старой системе, x 1 и y 1 – координаты точки в новой системе. Но поскольку ось OY в графическом окне Паскаля направлена вниз, то для её разворота вверх нужно, естественно, знак координаты y поменять на противоположный (вместо y поставить -y ). Таким образом, окончательно получим преобразование координат в графическом окне PascalABC.Net:
В результате последних преобразований вышеуказанная система координат будет иметь следующий вид:
Как мы видим, здесь начало координат перемещено в центр графического окна, а ось OY направлена вверх. В результате этого стали доступны не только положительные координаты, но также отрицательные.
Напишем простую программу, демонстрирующую все вышесказанное. Для этого, забегая наперед, укажем три полезные в графическом режиме PascalABC.Net процедуры:
Программа рисует окружность относительно графического окна (x 0 = 0, y 0 = 0), а через 3 секунды эта окружность появляется относительно нарисованной в центре системы координат. Перепишите эту программу в среду PascalABC.Net и запустите. Вот, собственно, сам код:
uses GraphABC ; const r = 90; //радиус окружности var x0 , y0 , x , y : integer ; begin x0 := WindowWidth div 2; //половина ширины окна y0 := WindowHeight div 2; //половина высоты окна x := 100; y := 100; //координаты центра окружности Line (x0 — 250, y0 , x0 + 250, y0 ); //ось OX Line (x0 , y0 — 200, x0 , y0 + 200); //ось OY Circle (x , y , r ); //окружность с центром (x, y) и радиусом r Circle (x , y , 2); //центр окружности (маленькая окружность) TextOut (x + 5, y , ‘(100, 100)’);//надпись возле центра окружности sleep (3000); //делаем паузу на 3 секунды ClearWindow ; //очищаем графическое окно белым цветом Line (x0 — 250, y0 , x0 + 250, y0 ); //ось OX Line (x0 , y0 — 200, x0 , y0 + 200); //ось OY x := x0 + x ; y := y0 — y ; Circle (x , y , r ); Circle (x , y , 2); TextOut (x + 5, y , ‘(100, 100)’); end.
Скопировать
**unit** GraphABC; : Модуль предоставляет константы, типы, процедуры, функции и классы для рисования в графическом окне **type** integer; : Представляет 32-битовое целое число со знаком. Диапазон значений: -2 147 483 648 .. 2 147 483 647 **function** WindowWidth: integer; : Возвращает ширину клиентской части графического окна в пикселах A **div** B — целочисленное деление А на В **function** WindowHeight: integer; : Возвращает высоту клиентской части графического окна в пикселах A **div** B — целочисленное деление А на В **procedure** Line(x1,y1,x2,y2: integer); : Рисует отрезок от точки (x1,y1) до точки (x2,y2) **procedure** Line(x1,y1,x2,y2: integer); : Рисует отрезок от точки (x1,y1) до точки (x2,y2) **procedure** Circle(x,y,r: integer); : Рисует заполненную окружность с центром (x,y) и радиусом r **procedure** Circle(x,y,r: integer); : Рисует заполненную окружность с центром (x,y) и радиусом r **procedure** TextOut(x,y: integer; s: string); : Выводит строку s в прямоугольник к координатами левого верхнего угла (x,y) **procedure** Sleep(ms: integer); : Делает паузу на ms миллисекунд **procedure** ClearWindow; : Очищает графическое окно белым цветом **procedure** Line(x1,y1,x2,y2: integer); : Рисует отрезок от точки (x1,y1) до точки (x2,y2) **procedure** Line(x1,y1,x2,y2: integer); : Рисует отрезок от точки (x1,y1) до точки (x2,y2) **procedure** Circle(x,y,r: integer); : Рисует заполненную окружность с центром (x,y) и радиусом r **procedure** Circle(x,y,r: integer); : Рисует заполненную окружность с центром (x,y) и радиусом r **procedure** TextOut(x,y: integer; s: string); : Выводит строку s в прямоугольник к координатами левого верхнего угла (x,y) Здесь необходимо сделать некоторые пояснения:
Нахождение длины окружности и площади круга на Паскаль
На следующей странице мы рассмотрим самое элементарное понятие в графике Паскаля – точки и пиксели, а также укажем полезные процедуры для работы с ними.
Источник: huncode.com
Процедуры Circle и Arc.
Процедура Circle вычерчивает на экране окружность. В качестве параметров этой процедуры используются координаты центра окружности и длина радиуса. Процедура Arc вычерчивает на экране дугу, у которой указываются координаты центра, начальный угол, конечный угол и длину радиуса.
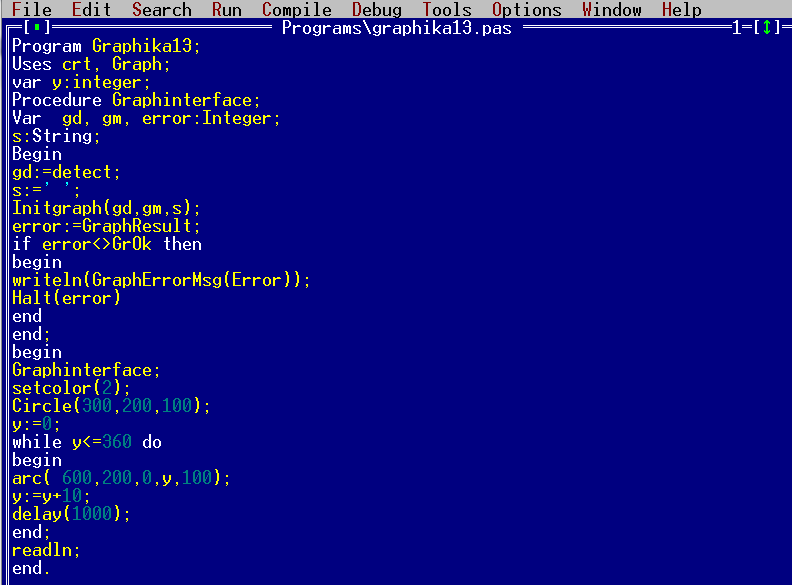
Рисование окружности и дуги с помощью процедур Circle и Arc.
Program Graphika13; Uses crt, Graph; var y:integer; Procedure Graphinterface; Var gd, gm, error:Integer; s:String; Begin gd:=detect; s:=’ ‘; Initgraph(gd,gm,s); error:=GraphResult; if error<>GrOk then begin writeln(GraphErrorMsg(Error)); Halt(error) end end; begin Graphinterface; setcolor(2); Circle(300,200,100); y:=0; while y
Строка №3. Указываем переменную для хранения значения конечного угла при построении дуги.
В строке №20 записываем процедуру SetColor. Она применима к процедурам Circle и Arc и будет определять цвет окружности и дуги, которые мы зададим в строках №21 и №25.
Строка №21. Процедура Circle рисует окружность на экране. После записи процедуры в круглых скобках указываются параметры процедуры. Первые 2 параметра определяют координаты X и Y для центра окружности (в нашем примере координата X имеет значение 300 пикселей, а координата Y – 200 пикселей).
Третий параметр процедуры Circle определяет радиус окружности (в нашем примере радиус имеет значение 100 пикселей). Таким образом, на экран выведется окружность зеленого цвета с центром в точке (300,200) и радиусом 100 пикселей.
Строка №22. Присваиваем переменной «y» начальное значение равное 0, т.е. конечный угол дуги равен 0.
Строка №23. Записываем цикл. Пока «y», т.е. конечный угол меньше либо равен 360 градусов, должно выполняться условие, которое следует за словом Do. За словом Do следуют 3 операции.
Строка №25. Первая операция – это процедура Arc, которая вычерчивает на экране дугу. Данная процедура имеет 5 параметров. Первые 2 параметра (в нашем примере 600,200) определяют координаты центра дуги. Третий параметр определяет начальный угол дуги в градусах (в нашем примере он равен 0).
Четвертый параметр определяет конечный угол дуги в градусах (в нашем примере он равен переменной «y»). Пятый параметр определяет радиус дуги (в нашем примере 100 пикселей).
Строка №26. Увеличиваем переменную «y» на 10 градусов. Благодаря тому, что строка №25 и №26 находятся в цикле, значение конечного угла будет увеличиваться от 0 до 360 с шагом в 10 градусов, причем это увеличение будут идти со скоростью 10 градусов в секунду благодаря процедуре Delay в строке №27. Таким образом, на экран выведется дуга с центром в точке (600,200) и радиусом 100 пикселей.
Начальный угол дуги будет равен 0 градусов. Конечный угол дуги также равен 0 градусов и растет на 10 градусов в секунду.
Дополнение к материалу.
Для процедур Circle и Arc можно установить толщину линии с помощью процедуры SetLineStyle, причем тип линии может принимать значение только solidln (сплошной), т.е. процедура SetLineStyle может иметь параметры либо (0,0,1), либо (0,0,3).
Источник: mojainformatika.ru
Учебник по программированию.
Здесь необходимо сделать небольшое пояснение. В данном параграфе кругом будем считать геометрическую фигуру круглой формы и закрашенную одним цветом. Окружностью будем считать линию, которая огибает круг и замыкается сама в себя. Не вникайте особо в слова, а взгляните на следующий рисунок и всё станет ясно:
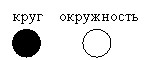
Рассмотрим процедуры рисования круга и окружности:
procedure DrawCircle (x,y,r: integer); – рисует окружность с центром (x,y) и радиусом r. Ширина окружности будет зависеть от настроек пера.
procedure FillCircle (x,y,r: integer); – рисует круг с центром (x,y) и радиусом r. В справочной системе про эту процедуру написано следующее: «заполняет внутренность окружности с центром (x,y) и радиусом r». На мой взгляд, начинающему программисту будет удобнее понимать, что данная процедура рисует именно круг определённого цвета, поэтому предлагаю на данном этапе именно так и понимать. Все остальные процедуры в данном параграфе будут так же описаны в моей интерпретации, т.к. это удобнее для понимания, и вы без особого труда сразу сможете начать ими пользоваться.
procedure Circle (x,y,r: integer); – рисует круг и окружность с центром (x,y) и радиусом r одновременно.
Прежде чем привести пример использования данных процедур нам необходимо познакомиться с понятием «кисть». Дело в том, что все примитивы можно подразделить на закрашенные фигуры и фигуры, состоящие из линии. Например, круг – закрашенная фигура, окружность – фигура, состоящая из линии.
Так вот все фигуры, состоящие из линии, рисуются пером, речь о котором шла в предыдущем параграфе, а все закрашенные фигуры закрашиваются кистью. Т.е. круг рисуется кистью, а окружность рисуется пером. Именно это и нужно уяснить из всего вышесказанного в данном абзаце.
Здесь же стоит сказать, что при рисовании текста, кисть закрашивает фон позади символов, установленным цветом в свойствах кисти. Чуть позже будет приведён пример и это будет показано наглядно. Так же стоит отметить, что изначально цвет кисти установлен белый, поэтому позади текста, который мы уже выводили в предыдущем параграфе, никакого закрашивания фона не происходило.
Подпрограммы для работы с кистью.
procedure SetBrushColor (c: Color); – устанавливает цвет кисти.
function BrushColor : Color; – возвращает цвет кисти.
procedure SetBrushStyle (bs: BrushStyleType ); – устанавливает стиль кисти.
function BrushStyle: BrushStyleType ; – возвращает стиль кисти.
Далее приведены константы стилей кисти:
- bsSolid сплошная кисть (по умолчанию);
- bsClear прозрачная кисть (на этом фоне будут видны предметы, которые были нарисованы ранее);
- bsHatch штриховая кисть;
- bsGradient градиентная кисть.
procedure SetBrushHatch (bh: HatchStyle ); – устанавливает штриховку текущей кисти.
function BrushHatch : HatchStyle ; – возвращает штриховку текущей кисти.
Далее константы стилей штриховки кисти:
- bhHorizontal ;
- bhVertical ;
- bhForwardDiagonal ;
- bhBackwardDiagonal ;
- bhCross ;
- bhDiagonalCross ;
- bhPercent05
- …
Стилей штриховки достаточно много, поэтому все их приводить не буду. Все стили можно просмотреть в справке в пункте: «Стандартные модули -> Модуль GraphABC -> GraphABC стили штриховки кисти». Или при наборе кода наберите bh и в всплывшей подсказке они все появятся.
Теперь можно привести пример рисования круга и окружности, а так же пример использования штриховки:
TextOut( 1 , 1 , ‘FillCircle(50,85,40);’ );
FillCircle( 50 , 85 , 40 );
TextOut( 150 , 1 , ‘Circle(200,85,40)’ );
Circle( 200 , 85 , 40 );
TextOut( 300 , 1 , ‘FillCircle(360,85,40);’ );
TextOut( 300 , 20 , ‘DrawCircle(360,85,40);’ );
FillCircle( 360 , 85 , 40 );
DrawCircle( 360 , 85 , 40 );
TextOut( 450 , 10 , ‘Использование штриховки.’ );
Circle( 520 , 85 , 40 );
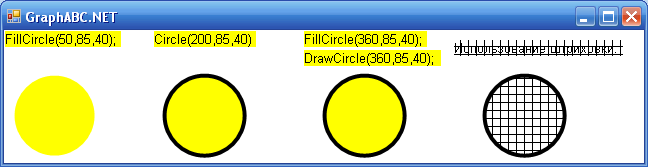
Обратите внимание на то, что над каждой фигурой (кроме последней) подписан код, с помощью которого была нарисована данная фигура. А так же на то, что штриховка производится чёрными линиями, а не жёлтыми. В GraphABC штриховка бывает только чёрная.
Дуга. Часть круга.
procedure Arc (x,y,r,a1,a2: integer); – рисует дугу окружности с центром в точке (x,y) и радиусом r, заключенной между двумя лучами, образующими углы a1 и a2 с осью OX (a1 и a2 – вещественные, задаются в градусах и отсчитываются против часовой стрелки).
procedure FillPie (x,y,r,a1,a2: integer); – заполняет внутренность сектора окружности, ограниченного дугой с центром в точке (x,y) и радиусом r, заключенной между двумя лучами, образующими углы a1 и a2 с осью OX (a1 и a2 – вещественные, задаются в градусах и отсчитываются против часовой стрелки).
procedure Pie (x,y,r,a1,a2: integer); – рисует заполненный сектор окружности, ограниченный дугой с центром в точке (x,y) и радиусом r, заключенной между двумя лучами, образующими углы a1 и a2 с осью OX (a1 и a2 – вещественные, задаются в градусах и отсчитываются против часовой стрелки).
procedure DrawRectangle (x1,y1,x2,y2: integer); – рисует контур прямоугольника.
procedure FillRect (x1,y1,x2,y2: integer); – рисует прямоугольник.
procedure Rectangle (x1,y1,x2,y2: integer); – рисует контур и прямоугольник одновременно.
Во всех этих процедурах (x1,y1) – координаты левого верхнего угла, (x2,y2) – координаты левого нижнего угла прямоугольника. Небольшое уточнение контур прямоугольника рисуется пером, сам прямоугольник – кистью.
Прямоугольник со скруглёнными краями.
procedure DrawRoundRect (x1,y1,x2,y2,w,h: integer); – рисует контур прямоугольника со скругленными краями.
procedure FillRoundRect (x1,y1,x2,y2,w,h: integer); – рисует прямоугольник со скругленными краями.
procedure RoundRect (x1,y1,x2,y2,w,h: integer); – рисует контур и прямоугольник со скругленными краями
Здесь (x1,y1) и (x2,y2) координаты верхнего левого и нижнего правого углов соответственно прямоугольника, из которого получается прямоугольник со скруглёнными краями. w и h – ширина и высота эллипса, используемого для скругления краев.
procedure DrawEllipse (x1,y1,x2,y2: integer); – рисует контур эллипса.
procedure FillEllipse (x1,y1,x2,y2: integer); – рисует эллипс.
procedure Ellipse (x1,y1,x2,y2: integer); – рисует контур эллипса и сам эллипс.
Здесь (x1,y1) и (x2,y2) – координаты левого верхнего и правого нижнего углов прямоугольника, который ограничивает рисуемы эллипс.
Далее пример, который демонстрирует работу процедур рисующих, часть круга, прямоугольника, прямоугольника со скруглёнными краями и эллипса:
Arc( 50 , 50 , 40 , 90 , 180 );
FillPie( 120 , 50 , 40 , 90 , 180 );
Pie( 190 , 50 , 40 , 90 , 180 );
DrawRectangle( 10 , 60 , 70 , 80 );
FillRect( 80 , 60 , 140 , 80 );
Rectangle( 150 , 60 , 210 , 80 );
//Прямоугольник со скруглёнными краями
DrawRoundRect( 10 , 90 , 70 , 110 , 20 , 5 );
FillRoundRect( 80 , 90 , 140 , 110 , 20 , 5 );
RoundRect( 150 , 90 , 210 , 110 , 20 , 5 );
DrawEllipse( 10 , 120 , 70 , 140 );
FillEllipse( 80 , 120 , 140 , 140 );
Ellipse( 150 , 120 , 210 , 140 );
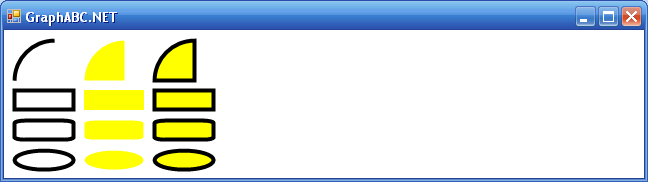
Заливка области заданным цветом.
Существует ещё одна хорошая процедура:
procedure FloodFill (x,y: integer; c: Color); – заливает определённым цветом замкнутую область, в которой находится точка с координатами x,y. Действие данной процедуры схоже с действием инструмента «Заливка» в стандартном приложении «Paint», которое есть в любом Windows. Например, нарисуем несколько кругов наезжающих друг на друга жёлтого цвета. Затем с помощью процедуры FloodFill перерисуем получившийся рисунок коричневым цветом. Так же стоит сказать, что данной процедурой можно установить цвет фона перед началом рисования. Пример:
FloodFill( 1 , 1 ,clRed);
FillCircle( 40 , 30 , 20 );
FillCircle( 70 , 30 , 20 );
FillCircle( 100 , 30 , 20 );
FloodFill( 40 , 40 ,clYellow);

