Программа mathematica что это

Иллюстрированный самоучитель по Mathematica 5

Mathematica – лучшая современная интегрированная система компьютерной алгебры

Что такое система Mathematica

Система Mathematica – это полностью интегрированная система компьютерной алгебры. Ее появление в 1988 году оказало очень большое влияние на использование компьютеров в науке и технике. Часто говорят, что именно появление системы Mathematica открыло эру применения компьютерной алгебры в научных и технических вычислениях.

Концепция системы Mathematica

Специализированные пакеты для решения численных, алгебраических, графических и других задач появились еще в 60-х годах прошлого столетия. Но система Mathematica отличается от них концептуально: система Mathematica универсальна, так как она предназначена для любых научных и технических вычислений. Для этого в ней предусмотрен язык компьютерной алгебры, который позволяет описать широкий круг объектов, которые могут потребоваться в научных и технических вычислениях, причем в самом языке используется очень малое число первичных объектов.

КиЯ 0.17 | Списки как векторы и матрицы, элементы линейной алгебры в Wolfram Language

Применение системы Mathematica

Хотя первыми пользователями системы Mathematica были инженеры, физики и математики, область ее применения быстро расширилась. Сегодня едва ли можно указать область, в которой программа Mathematica не применяется, ее используют физики, биологи, социологи, инженеры, студенты и школьники, хотя последним пользоваться подсказками этой системы часто запрещается.

Программа Mathematica сыграла решающую роль во многих важных научных открытиях и стала стандартным инструментом многих инженеров. Она широко используется в планировании и финансовом анализе, с ее помощью исследовались многие сложные финансовые модели. И, конечно же, система Mathematica стала важным инструментом информатики. Результаты, получаемые с ее помощью, используются также для создания новых, более совершенных версий этой системы.

Кто использует систему Mathematica

Основная часть пользователей системы Mathematica состоит из профессионалов. Но Mathematica также широко используется в образовании; существует несколько сотен курсов для высшей и средней школы, основанных на ней. С появлением студенческой версии системы, Mathematica стала важным инструментом для студентов по всему миру. Кроме того, она является стандартом для множества организаций и крупнейших университетов мира.

Развитие системы Mathematica

Mathematica признана фундаментальным достижением в области компьютерного проектирования. Она является одной из самых больших программ и содержит огромное число алгоритмов и технических новшеств. Среди этих новшеств – независимый от платформы интерактивный документ, называемый блокнотом. Блокноты стали стандартом для многих видов отчета и используются для публикации технических документов.

Mathematica была создана компанией Wolfram Research. Успех системы Mathematica привел к росту компании и появлению большого числа независимых разработчиков, связанных с системой Mathematica. Сегодня существует более сотни специализированных коммерческих пакетов для программы Mathematica, а также несколько периодических изданий и несколько сотен книг, посвященных этой системе.

1: Знакомство с Wolfram Mathematica. Галопом по Европе

Расширение системы Mathematica

Mathematica – это расширяемая система. Кроме внутренних команд ядра системы Mathematica, можно использовать дополнительные команды, которые содержатся в загружаемых пакетах. Некоторые пакеты системы (по алгебре, анализу и т.д.) поставляются вместе с самой программой и являются стандартными. Другие пакеты можно переписать с сервера компании Wolfram Research (www.wolfram.com) или приобрести отдельно.

Чтобы выполнить команду из пакета Mathematica, надо сначала загрузить нужный пакет с помощью команды или .

Последняя команда инициализирует все пакеты из папки dir. Вот как, например, можно инициализировать все алгебраические пакеты: .

Источник: samoychiteli.ru

Введение в Wolfram Mathematica

На хабре уже не раз упоминалась Mathematica и если вам хочется начать работать с ней, то эта статья для вас. Я расскажу об основных аспектах работы с нею и покажу несколько интересных нововведений из последних версий Wolfram Mathematica.

Wolfram Mathematica — это программное обеспечение, не только для математических вычислений, это гораздо больше: от моделирования и симуляции, визуализации, документации, до создания веб-сайтов. Mathematica обладает возможностью осуществлять вызовы функций и принимать вызовы с C, .NET, Java и других языков, генерировать C код, компилировать автономные библиотеки и исполняемые файлы.
Обо всех достоинствах Mathematica можно почитать на официальном сайте

Для начала работы с Mathematica вам необходимо её получить и установить на свой компьютер. Mathematica прекрасно работает на Windows, Mac, Linux.
Скачать и бесплатно попробовать Mathematica так же можно на оф. сайте.
Если же вы надумаете её купить, то цены на неё вполне приемлемые. Например для студента за семестровый вариант она обойдётся в $44.95. Для домашнего использования в $295. Если вы планируете использовать её для коммерческих целей, то наилучший вариант лицензии это Standard Edition (Вы получаете подписку на Premier Service и бесплатные обновления).

Изучение

Самая лучшая книга по Mathematica — это встроенный Help. Имеет огромную кучу туториалов и советов. Огромное множество примеров. Всё что вам может понадобится находится там. Это первое место где нужно искать нужную информацию.

Однако, если вам нужно больше, в интернете огромное множество сообществ посвещённых Mathematica. (Например: mathematica.stackexchange.com).

Блокноты и Ячейки

• Ячейки ввода – в них задаются команды, которые будут вычислены
• Ячейки результата – в них выводится результат вычислений
• Другие ячейки – ячейки с текстом, заголовки и все остальное

Нумерация ячеек идёт в том порядке в котором вы их запустили. Для того что-бы вычислить значение ячейки нажмите SHIFT+ENTER или правый ENTER, либо Evaluation -> Evaluate Cells.

Для того что-бы обратиться к значению последней вычисленной ячейке используйте знак %.

Бесконечная точность

Одной из замечательных особенностью Mathematica является концепция бесконечной точности. Если результатом вычислений является корень из двух, то она так и напишет.

Вы можете попросить округлить ответ так:

Или же добавить дробную часть (или просто точку) к числам в выражении:

Ввод формул

В Mathematica реализован удобный ввод формул. Но для начала вам могут пригодится палитры (На картинке справа находится Palettes -> Basic Math Assistant).

У каждой кнопочки на палитре, есть свой горячие клавиши. Например, что бы написать знак интеграла нужно нажать Esc int Esc.

Вот список наиболее часто используемых горячих клавиш:

• CTRL+2 – Шаблон квадратного корня
• CTRL+6 – Верхний индекс
• CTRL+7 – Надстрочный символ
• CTRL+- – Нижний индекс
• CTRL+= – Подстрочный символ
• CTRL+/ – Дробь
• CTRL+2, затем CTRL+5 – Корень любой степени
• ALT+ENTER – Создает новую ячейку
• SHIFT+CTRL+D – Разбивает текущую ячейку
• SHIFT+CTRL+M – Склеивает несколько ячеек

Выражения, Списки, Функции

Все что записано внутри ячеек является выражениями. Каждое выражение состоит из головы и списка. Например в выражение Power[2, 2]. В нём головой является Power, а списком 2, 2.
Даже 2+2 является выражением. Чтобы посмотреть как Mathematica интерпретирует ввод, есть функция FullForm:

Функция Hold просит математику не вычислять выражение. Обратной функция является Evaluate.

Списки в Mathematica создаются при помощи фигурных скобок: <. >, что является сокращением от List[. ].

Для манипуляции со списками в Mathematica есть огромная куча функций. Всё что вам может когда-нибудь понадобиться уже есть там. Вам остаётся только найти нужную функцию.

Для того чтобы получить элемент списка есть функция Part, c сокращённым вариантом в виде двойных квадратных скобок [[. ]] либо с толстыми скобками (Esc [[ Esc).

Поскольку всё является выражениями (и списки тоже), мы может получить голову выражения таким вот способом:

Таким образом индекс первого элемента в списке это 1.

А так же инфикс: из x ~ f ~ y получим f[x, y].

Однострочное программирование

В Mathematica есть множество функций для обычного программирования, такие как For, If, Switch. Однако, их лучше не использовать без крайней необходимости. Так как практически всё тоже самое можно сделать в одну строчку при помощи специальных функций и их комбинированием (поначалу бывает сложно перестроиться на такой стиль программирования).

Вот хорошее видео демонстрирующее как работают некоторые из функций:

Динамические интерактивные вычисления

Одной из замечательнейших возможностью Mathematica, являются динамические вычисления. Они позволяют манипулировать данными и смотреть на то как динамически меняется результат.

Для динамических вычислений используются функции Dynamic, Manipulate и др.

Заключение

В статье я рассказал о основных аспектах работы в Mathematica. Есть также несколько других важных моментов, таких как паттерны, модули, ядра. О них я расскажу в следующий раз, если эта тема будет интересна вам.

PS Обо всех найденных ошибках сообщайте мне в личку.

UPDATE
Картинки исчезли. Восстановил пост в своём блоге elfet.ru/introduction-to-wolfram-mathematica

• Программирование
• Математика

Источник: habr.com

Wolfram Mathematica

Доступно для
рабочего стола, облака и
мобильных устройств

Wolfram Mathematica

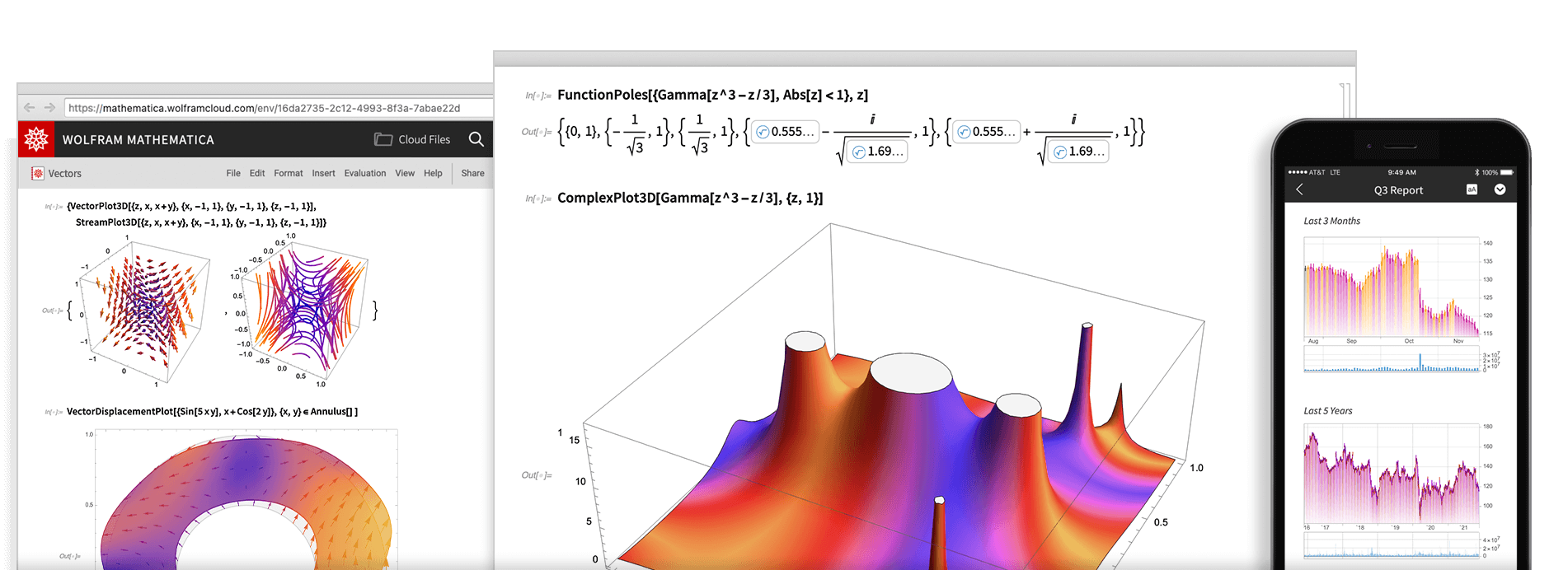
На протяжении трёх десятилетий система Mathematica определяет передовой край технических вычислений и обеспечивает основную среду для проведения расчётов для миллионов новаторов, педагогов, студентов и других пользователей по всему миру.

Широко признанная за технические возможности и элегантную простоту использования, система Mathematica обеспечивает цельную интегрированную и постоянно расширяющуюся систему, охватывающую весь спектр технических вычислений, а также доступна бесперебойно в облаке через любой веб-браузер наряду со всеми родными современными системами для рабочего стола.

Нет лучшего выбора для современных технических вычислений

Благодаря энергичному развитию и стабильному видению на протяжении трёх десятилетий, система Mathematica не имеет себе равных в большом диапазоне измерений и уникальна в своей поддержке современной среды и организации рабочего процесса для технических расчётов.

Огромная система, тесная интеграция

Mathematica имеет в наличии более 6000 встроенных функций, покрывающих все области технических расчётов—все они тщательно интегрированны для идеальной совместной работы, и все они включены в полностью интегрированную систему Mathematica.

За пределами чисел и математики

Основываясь на трех десятилетиях развития, система Mathematica превосходит во всех областях технических расчётов, включая нейронные сети, машинное обучение, обработку изображений, геометрию, науку о данных, визуализацию и многое другое.

Удивительная алгоритмическая производительность

Система Mathematica строится на беспрецендентно мощных алгоритмах всех предметных областей; многие из них были созданы компанией Wolfram, используя уникальные методы развития и уникальные возможности языка Wolfram Language.

Более высокий уровень, чем когда-либо прежде

Суперфункции, мета-алгоритмы. Mathematica предоставляет прогрессивную высокоуровневую среду с максимальным уровнем автоматизации, что позволяет Вам быть наиболее продуктивными.

Вся функциональность промышленного класса

Mathematica построена с целью предоставления возможностей промышленной мощности, с крепкими эффективными алгоритмами во всех областях, способными решать крупномасштабные задачи с параллелизмом, вычислениями на графических процессорах и многим другим.

Убедительная простота в использовании

Система Mathematica использует свои алгоритмические возможности и тщательное проектирование языка Wolfram Language для создания уникальной в использовании системы, имеющей предиктивные рекомендации, поддержку ввода на естественном языке и многое другое.

Не только пишите код, но и документируйте

Понятный код

Благодаря когерентному дизайну и использованию интуитивных названий функций, состоящих из полных английских слов, язык Wolfram Language исключительно просто читать, использовать и изучать.

Представляйте свои результаты наилучшим способом

Благодаря утончённой вычислительной эстетике и отмеченному наградами дизайну, система Mathematica представляет Ваши результаты в прекрасном виде, мгновенно создавая передовые интерактивные визуализации и готовые к публикации документы.

Реальные данные напрямую

Mathematica имеет доступ к обширной базе знаний Wolfram Knowledgebase, которая включает актуальные реальные данные из тысяч предметных областей.

Эффективная облачная интеграция

Система Mathematica теперь плавно интегрированна с облаком, позволяя совместное использование, облачные расчёты и многое другое в уникальной и мощной гибридной среде облака/рабочего стола.

Совместимо с чем угодно

Система Mathematica построена так, чтобы быть подключенной ко всему: файловым форматам (более 180), другим языкам, Wolfram Data Drop, API, базам данных, программам, интернету вещей, устройствам и даже распределённым копиям самой себя.

Более 150 000 примеров

Начните с практически любого проекта с помощью более 150000 примеров из Documentation Center, и более 10000 демонстраций с открытым кодом в Wolfram Demonstrations Project и множества других ресурсов.

Функциональное покрытие

Mathematica основывается на инновационном языке Wolfram Language.

Источник: www.wolfram.com

Первое знакомство с Mathematica

Аннотация: В настоящей лекции мы впервые познакомимся с пакетом Mathematica, её возможностями при выполнении вычислений, узнаем некоторые встроенные функции. Мы научимся осуществлять элементарные математические операции, «задавать вопросы» Mathematica (вводить данные) и «получать ответы» (получать результат вычислений), а также пользоваться встроенной документацией, расширяющей возможности пользователя при работе пакетом.

Цель лекции: познакомиться с основными возможностями пакета и базовыми принципами работы в системе компьютерной алгебры Mathematica.

1.0. Введение: Основные возможности системы компьютерной алгебры Mathematica

Пакет Mathematica совершенствуется и развивается уже не одно десятилетие, начиная с конца восьмидесятых годов прошлого века. За эти годы Mathematica из программируемого калькулятора, однако, уже тогда способного на многое в математике, выросла в полноценную систему компьютерной алгебры.

Все возможности Mathematica можно разделить на 4 больших категории: численные расчёты, символьные вычисления, визуализация и программирование . Краткую обобщённую классификацию возможностей Mathematica приводят А.Н. Прокопеня и А.В. Чичурин в книге [5, с. 6–7]. В редуцированном виде приведём её в нашем курсе.

1. Численные расчеты
2. Mathematica позволяет производить вычисления с любой точностью. Это отличает её от обычного калькулятора, для которого точность вычислений фиксирована. Также Mathematica может производить расчеты с использованием специальных функций.
3. Mathematica умеет вычислять интегралы, численно решать алгебраические и дифференциальные уравнения и системы уравнений.
4. Mathematica позволяет производить статистический анализ численных данных, производить Фурье-анализ, интерполяцию и аппроксимацию данных с помощью метода наименьших квадратов.
5. Mathematica прекрасно работает не только с числами, но и с матрицами, обеспечивая выполнение всех операций линейной алгебры.

• Mathematica позволяет оперировать алгебраическими формулами: разлагать на множители, раскрывать скобки или напротив, производить упрощение многочленов и т.д.
• Mathematica позволяет находить решения дифференциальных уравнений, находить интегралы и производные в символьном виде.
• Mathematica может разлагать функцию в ряд, вычислять пределы.

• Mathematica умеет строить двух- и трехмерные графики аналитических функций, заданных явно или параметрически, а также контурные и плотностные графики. Помимо функциональных зависимостей Mathematica умеет визуализировать дискретные наборы данных.
• Mathematica обладает значительным набором инструментов, опций, позволяющих контролировать оформление изображений, графиков. Так, например, можно изменять цвет графиков, управлять тенями, освещением и яркостью и т.д.
• Mathematica позволяет строить изображения, используя элементарные графические объекты, стандартные фигуры. В двумерной графике это — многоугольники, окружности, дуги и т.д., в трёхмерной графике — параллелепипеды, сферы, цилиндры, конусы и т.д. Также Mathematica позволяет добавлять текстовые комментарии в любое место двумерного или трехмерного графического объекта.

• Mathematica позволяет создавать дополнительные функции под нужды пользователя. Использование именно этой возможности подразумевает функциональный стиль программирования.
• Mathematica обладает таким инструментом, как правила преобразований, которые позволяют одним символьным выражениям ставить в соответствие другие символьные выражения и численные значения. На этой возможности базируется так называемый стиль программирования, основанный на правилах преобразования.
• В Mathematica содержится большое количество встроенных функций, позволяющих разветвлять вычисления в зависимости от выполнения определённых условий, многократно выполнять тот или иной алгоритм действий, реализуя тем самым процедурный стиль программирования.
• Mathematica сама по себе представляет собой язык программирования высокого уровня, на котором можно писать как малые, так и большие программы.

1.1. Начало работы в Mathematica. Интерфейс программы

1.1.1.Главное меню программы

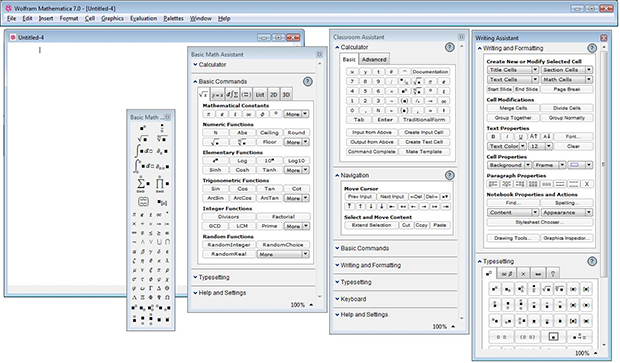
Mathematica, как и всякая программа, предназначенная для выполнения под Windows, запускается после двойного щелчка кнопкой мыши на соответствующей пиктограмме. На рис. 1.1 приведён снимок экрана с запущенной программой Mathematica. Основные элементы интерфейса программы следующие: в самом верху экрана располагается строка главного меню, белая прямоугольная область в средней части экрана — окно редактирования или окно ввода; тяготеющие к правой части экрана окна — палитры.

Начнём описание интерфейса программы с главного меню.

Пункты главного меню Mathematica достаточно подробно описаны в книгах А. П. Мостовского [4, с. 6–8] и А. В. Чигарева [6, с. 115–124].

Пункт меню File предназначен для работы непосредственно с файлами программы. С его помощью можно, например, создавать новые файлы ( New ), выбирать из каталога ранее уже созданные ( Open. ), сохранять файлы ( Save As ), перезаписывать ( Save ) или закрывать их без сохранения ( Close ), управлять параметрами представления данных на экране ( Printing Settings ), печатать документы ( Print. ) и завершать работу всей программы ( Exit ).

Пункт меню Edit содержит основные операции редактирования данных на экране. Среди них отмена операции ( Undo ), копирование фрагментов документа в буфер обмена с их удалением из текста программы ( Cut ) и без удаления ( Copy ), вставка фрагментов из буфера обмена в заданную область документа ( Paste ), удаление фрагментов документа ( Clear ). Помимо этого, в данном пункте меню содержатся команды для поиска выражений в тексте программы: это Find. для задания шаблона для поиска, а также Find Next и Find Previous для перехода к следующему и предыдущему фрагментам текста, соответственно, совпадающим с шаблоном. Подпункт Preferences. ответственен за управление настройками самого пакета.

При помощи команд, содержащихся в пункте меню Insert , можно вводить данные в окно редактирования. Например, можно задавать верхние и нижние индексы при помощи содержащихся в подпункте Typesettings команд Superscript и Subscript , обособлять тексты скобками различного вида при помощи команд Matching [], Matching (), Matching <> и т.д. Можно вставлять в текст программы объекты, созданные в других программах, например, графику, формулы и т.д.

Управлять ячейками данных позволяет пункт меню Cell (подробней о ячейках см. пункт 1.1.2 настоящей лекции). С его помощью можно устанавливать формат ячеек ( Cell Properties ), преобразовывать их тип ( Convert To ), группировать ( Grouping ), объединять ( Merge Cells ) и разделять ( Divide Cells ) ячейки и т.д.

Пункт меню Graphics , что весьма очевидно, отвечает за работу с графическими данными, встречающимися в тексте программы.

В пункте меню Evaluations собраны команды для непосредственного управления ходом вычислений, работой с ядром программы. С их помощью можно осуществлять вычисления в пределах одной ячейки программы ( Evaluate Cells, Evaluate Initialization Cells ), в пределах всей программы ( Evaluate Notebook ), отключать ядро ( Quit Kernel ) программы и вновь запускать его ( Start Kernel ) и т.д.

Ввод данных в окно ввода в Mathematica можно осуществлять не только вручную с клавиатуры, но и с использованием так называемых палитр ( Palettes ). Они представляют собой окна, содержащие набор кнопок, за которыми закреплены определённые действия, и выпадающих списков. Управлять палитрами можно, используя команды в пункте меню Palettes . Можно выводить на экран и убирать с экрана те или иные палитры, а также создавать собственные палитры с требуемым набором функций.

Команды для управления внешним видом окон, их расположением, собраны в пункте меню Window . Содержание этого пункта типично для большинства программ, предназначенных для работы в ОС Windows.

Последний пункт меню, Help , содержит команды для работы со справочными данными по пакету Mathematica.

В любом из пунктов меню часть команд в настоящий момент может быть невыполнима — например, нельзя вычислить значение выражения, если само оно в окно редактирования ещё не введено, либо не выделена содержащая его ячейка. Такие команды выделяются светло серым шрифтом.

увеличить изображение
Рис. 1.1. Скриншот открытых окон запущенного приложения Mathematica. В зафиксированный момент на экране присутствуют главное меню, окно ввода, и окна палитр функций

1.1.2. Окно ввода

Все элементы интерфейса Mathematica выводятся независимо друг от друга: отдельно — строка меню, отдельно — окна (в том числе окно редактирования), отдельно палитры инструментов. В одно и то же время на экране могут быть представлены одни элементы, и скрыты другие. Кроме того, можно, перетаскивая мышкой, помещать элементы программы в любое удобное место экрана, изменять их размеры (В. П. Дьяконов [2, с. 35–37]). В окне редактирования имеются полосы прокрутки для скроллинга не помещающихся на экране текстов.

Все введённые в окно ввода данные в Mathematica содержатся в отдельных, определённым образом выделенных областях экрана, называемых ячейками. Итак, программа запущена, и в центральной части экрана появилась девственно чистая область — окно ввода. Именно в эту область и предстоит вводить данные. Как только будет введён первый символ, в правой части окна ввода появится квадратная скобка: она обозначает вертикальные границы ячейки, содержащей введенный с клавиатуры символ. Исходные данные содержатся во входных ячейках ( Input ), а результат преобразований — в выходных ( Output ). А. П. Мостовской в [4, с. 6] определяет ячейку в Mathematica следующим образом: «Под ячейкой понимается связная часть рабочего поля, содержащая задачу, ответ, текст или другое».

После того, как на экране появилось окно редактирования (при первом старте Mathematica или после выбора подпункта New в пункте меню File ), вы сразу же можете вводить данные. Например, если вы наберёте N[E,10] и нажмёте Shift+Enter (удерживая Shift , нажмёте Enter ) для начала вычислений, Mathematica выведет на экран приближённое значение экспоненты с точностью до 10-и значащих цифр — см. рис. 1.2.

Рис. 1.2. Экспонента с точностью до 10-и значащих цифр

Таким образом, чтобы Mathematica произвела вычисление введённого выражения, необходимо, оставив курсор внутри ячейки с входными данными, нажать сочетание клавиш Shift+Enter . Заметим, что после того, как вы заставили программу произвести вычисления в окне редактирования, Mathematica добавляет к данным на экране подсказки в виде In[1]:= для входных данных, и Out[1]:= для данных на выходе, т.е. результатов вычислений — также см. в качестве примера рис. 1.2. При этом исходное значение оказывается присвоенным объекту In[1] , а результат вычислений — объекту Out[1] (Е. М. Воробьёв [1, с. 8–9]). В нашем примере на рис. 1.2 в текущей сессии работы с программой ввод с клавиатуры In[1] будет эквивалентен вводу выражения N[E,10] , а ввод Out[1] — вводу 2.718281828 .

Скажем ещё несколько слов о скобке в правой части экрана, очерчивающей границы ячейки с входными данными и результатами их преобразований. Если все заданные вычисления завершены успешно или ещё не проводились, ячейка обозначается тонкой правой квадратной скобкой, цвет которой зависит от цветовой схемы, используемой в операционной системе пользователя (см. пример на рис. 1.2).

Изменение внешнего вида скобки может многое сказать о текущем состоянии вычислений. Если скобка изменила цвет на яркий, привлекающий внимание, и толщину, а в верхней её части появился значок + , это значит, что в синтаксисе содержащихся в ячейке выражений имеется ошибка: узнать на характере ошибки можно, нажав на + (см. верхний пример на рис. 1.3).

Эта скобка также оказывается полезной при организации работы с большим количеством разнородных данных. Двойной клик на скобке позволяет свернуть ячейку, содержащаяся в которой информация, например, в данный момент не используется, и в представлении её на экране нет необходимости. И напротив, двойной щелчок позволяет развернуть свёрнутую ранее ячейку.

Новые данные можно вводить непосредственно под ячейкой с предыдущими вычислениями, ограниченной снизу горизонтальной линией, проходящей по всей ширине окна ввода. Новая ячейка откроется сразу же, как только вы начнёте вводить данные.

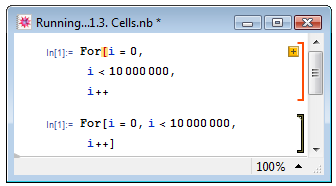
Рис. 1.3. Разные типы скобки, очерчивающей ячейку

1.1.3. Палитры математических функций

В данной лекции мы уже упомянули такой термин, как палитры. В Mathematica палитра — панель с кнопками быстрого управления.

С одной стороны, кажется удобным, когда элементы управления находятся на экране, перед глазами, и вместо того, чтобы вспоминать команду для выполнения того или иного действия, достаточно нажать соответствующую кнопку на экране. Однако, с другой стороны, когда таким способом упрощён ввод большого количества команд, экран оказывается сильно загромождён этими вспомогательными панелями.

Разработчики Mathematica сумели реализовать положительный эффект от вспомогательных панелей, минимизировав причиняемые им неудобства. Они создали инструментальные палитры, содержащие определённым образом сгруппированные команды для ввода математических выражений, отсутствующих на клавиатуре символов, команд управления вычислениями, инструментов работы с текстом и графикой. Палитрам не обязательно всё время находиться на экране, и по желанию пользователя они могут быть перемещены в любое место экрана или вовсе скрыты. Управлять палитрами можно при помощи команд, собранных в пункте главного меню Palettes .

На скриншоте на рис. 1.1 представлено несколько палитр, имеющихся в Mathematica.

Источник: intuit.ru

Wolfram Mathematica

Вычислительная многофункциональная система Wolfram Mathematica известна как мощнейшая исследовательно-математическая платформа.

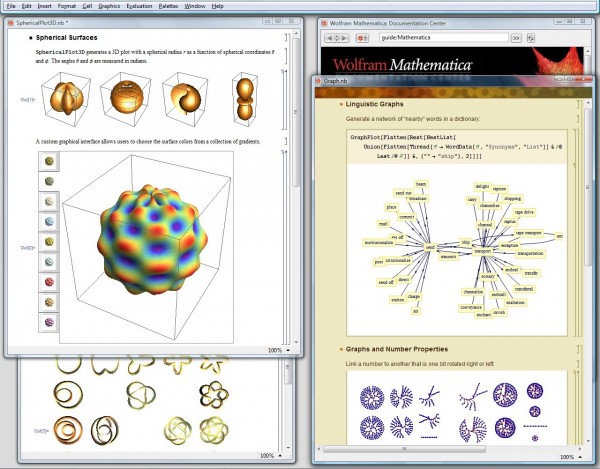
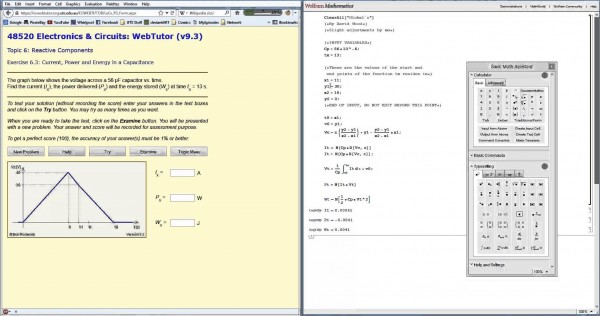
Программный пакет применяется повсеместно при расчетах от ежедневных студенческих задачек, до ультрасовременных научных исследований. Серьезные вычислительные комбайны, претендующие на лидерство мирового уровня, своим внушительным набором возможностей могут несколько обескуражить простого пользователя.

В свою очередь, любая ответственная лаборатория, кафедры вузов, инженерные компании остро заинтересованы в автоматизированном произведении расчетов любой степени трудности. По этой причине, несмотря на цели и намерения, системы программного обеспечения Wolfram Mathematica просты в эксплуатации и могут использоваться обширной категорией пользователей: преподавателями, инженерами и даже обыкновенными учащимися школ.

Все они могут извлечь очевидную выгоду от удобного использования данного приложения.

Притом, огромное множество заложенных функций не перегружает саму программу, следовательно, не замедляет вычисления. А установочный файл Wolfram Mathematica скачать бесплатно можно, прибегнув к ссылке ниже. Программа имеет отточенную правильность и непревзойденную скорость расчетных операций, что дает возможность полноценной работы как на современных, мощных ПК, так и на более слабых машинах.

Центральным местом в утилитах класса вычислительных систем всегда является собственное машинно-независимое ядро всех математических операций. Здесь ядро сделано определенным образом, чтобы можно было вызывать команды управления программой без задержек. Для расширения стандартных программных ресурсов служит специализированная библиотека и набор пакета с расширениями.

Эти вспомогательные расширения готовятся на собственном программном языке систем Wolfram Mathematica и являются ключевым средством для всестороннего развития общего функционала и полной адаптации к решению любой пользовательской задачи. Помимо прочего, у приложения имеется развернутая электронная справочная помощь (Help), содержащая информационные материалы с конкретными примерами.

Таким образом, Wolfram Mathematica как целостный модуль программирования располагает всеми возможностями и средствами для позиционирования на рынке как сильнейший математический инструментарий, служащий неоценимым помощником в любых условиях, для любого пользователя.

Обновленное издание приложения включает нововведения, такие как: визуализация векторных полей, статистический анализ моделей, полная поддержка сплайнов, не исключая NURBS, а также некоторые алгоритмы булевой алгебры.

Источник: soft-file.ru