Программа кузнечик что это

Примеры решения задач с кузнечиком

Решение задач с кузнечиком — это решение задач методом динамического программирования.

Динамическое программирование

Проблемы, где возможны несколько допустимых решений, предполагают возможность выбора одного самого лучшего итогового результата, который может быть осуществлён в теории путём перебора всех возможных вариантов и выбором самого лучшего. Но если объёмы исходных данных достаточно велики, то метод полной переборки вариантов не станет оптимальным по временным затратам.

Замечание 1

В таких случаях обычно применяется разбиение большой задачи на ряд более мелких подзадач. Этот способ разрешения больших задач именуется динамическим программированием.

Решим твою учебную задачу всего за 30 минут
Попробовать прямо сейчас

Не все задачи могут быть сведены к динамическому программированию. Задачи, которые возможно решить этим методом, обязаны иметь такие характеристики:

1. Задачу можно разбить на ряд подзадач похожего структурного построения, но более маленького объёма.
2. В сформированном наборе подзадач можно обнаружить подзадачи с тривиальным уровнем сложности, то есть маленькие и обладающие очевидным решением.
3. Наилучшее решение больших подзадач возможно сформировать на базе решений более мелких подзадач.
4. Все подзадачные решения возможно представить и сохранить в табличном формате, который имеет не бесконечные размеры.

Все проблемы из сферы динамического программирования можно разделить на два вида:

КУЗНЕЧИК ПРОТИВ саранчи, сверчков, цикады, богомола и даже ящерицы. Кузнечик и Сверчки в деле!

1. Определение числа возможных версий решения. То есть, в данном варианте вычисляется общее число решений.
2. Выбор наилучшего решения. В данном варианте оптимизируется целевая функция, то есть находится наилучшее решение из всех возможных решений.

Задача о кузнечике

Задачи, где необходимо найти самое лучшее решение среди множества допустимых вариантов, наиболее просто решаются посредством динамического программирования. Приведём пример задачи поиска оптимального решения на основе задачи о кузнечике, собирающем монеты.

«Примеры решения задач с кузнечиком»
Готовые курсовые работы и рефераты
Консультации эксперта по предмету
Помощь в написании учебной работы

Условия задачи следующие. Кузнечик выполняет серию прыжков по столбам, которые располагаются в ряд по единой линии и на одинаковых дистанциях между ними. Столбы пронумерованы и это номера од единицы до N.В исходном положении кузнечик находится на столбе пол номером один.

Он способен совершить прыжок вперёд на дистанцию от одного до К столбов, отсчитывая от текущего его местоположения. При этом, находясь на каждом столбе, у кузнечика есть возможность приобрести или потерять некоторое количество золотых монет. Эта возможность заранее известна для каждого столба. Требуется определить маршрут прыжков кузнечика, чтобы он собрал при этом максимальную сумму золотых монет. При этом существует условие, что прыжки кузнечику разрешены только вперёд.

Кузнечик — интересные факты

Рассмотрим исходные данные. В начальной строке можно ввести два натуральных числа N и K (2 ≤ N, K ≤ 10000), которые разделяются при помощи пробела. В следующей строке надо записать также через пробелы N – 2 целых чисел. Это число монет, которые приобретёт кузнечик на каждом столбе, начиная со второго и до N – 1. В случае отрицательного значения числа на столбе, кузнечик потеряет монеты. Есть гарантия, что модуль каждого числа не более десяти тысяч.

Рассмотрим выходные данные. Изначально программе необходимо определить какое самое большое число монет возможно собрать кузнечику. Вторая строка программы должна вычислить количество прыжков кузнечика, а затем определить нумерацию всех столбов, посещённых кузнечиком (по возрастанию номеров через пробелы). При этом, в случае наличия более одного верного решения, можно вывести любое из найденных.

Чтобы решить поставленную задачу, воспользуемся динамическим массивом d[ ]. Здесь d[i] является самым большим количеством золотых монет, которые возможно приобрести кузнечику при нахождении его в текущий момент на столбе i. Исходное наполнение динамического массива: d[1]=0, то есть при расположении кузнечика на первом столбе у него в наличии нуль золотых монет. Определим правило изменения динамического массива:

здесь num_max – это нумерация столба, где кузнечик собрал наибольшее число золотых монет, и который был до текущего. То есть, при расположении кузнечика на i-том столбе, ему возможно приобрести самое большое число золотых монет, которое равняется сумме предшествующего самого большого числа монет плюс число монет текущего столба. Решением задачи станет число d[n], где n – номер конечного столба.

Рисунок 1. Решение задачи. Автор24 — интернет-биржа студенческих работ

Источник: spravochnick.ru

Программа кузнечик что это

Цели. Познакомиться с исполнителем Кузнечик, с его операторами. Решение задач на исполнителе Кузнечик. Создание задач на исполнителе Кузнечик.

Для знакомства с исполнителем Кузнечик из главного окна КуМира вызовите описание командами

Инфо → Описание миров → Кузнечик.

Из окна Кузнечика из меню Задания задайте длины прыжков, начальное положение, область, доступную Кузнечику, флаги.

С помощью пульта произвольно выполните управление Кузнечиком, используйте прыжки, закрашивание и стирание координат.

Откройте окно исполнителя Кузнечик.

Установите задания: прыжок вперёд (вправо) на 2, прыжок назад (влево) на 1, начальное положение в 0, область от -10 до 10.

Откройте пульт для исполнителя Кузнечик.

Используя пульт, напишите алгоритм для закрашивания всех нечётных координат. Составьте программу, используя оператор цикла.

Откройте окно исполнителя Кузнечик

задании Установите задания так, что Кузнечик умеет выполнять команды «вперед 3», «назад 4», начальное положение в 33. Используя команды исполнителя Кузнечик, напишите алгоритм для получения из числа 33 числа 4 (без использования пульта).

Исполнитель КУЗНЕЧИК живёт на числовой оси. Начальное положение КУЗНЕЧИКА – точка 0. Система команд Кузнечика:

Вперед 4, Назад 3.

Какое наименьшее количество раз должна встретиться в программе команда «Назад 3», чтобы Кузнечик оказался в точке 27? Составьте программу.

Исполнитель КУЗНЕЧИК живёт на числовой оси. Начальное положение КУЗНЕЧИКА – точка 0. Система команд Кузнечика:

Вперед 3, Назад 4.

Какое наименьшее количество раз должна встретиться в программе команда «Назад 4», чтобы Кузнечик оказался в точке 31? Составьте программу.

Переместить Кузнечика из точки 0 в точку 10, в точки с флажками не заходить, закрасить точку 10.

Условия: исходная позиция – точка 0; Вперед 3, Назад 2, Флажки – в точках 3, 7.

Задание 6. Составьте интересное на Ваш взгляд задание для Кузнечика, которое имеет небольшое количество решений.

Источник: www.sites.google.com

Криптографический алгоритм «Кузнечик»: просто о сложном

В данной статье будет подробно рассмотрен алгоритм блочного шифрования, определенный в ГОСТ Р 34.12-2015 как «Кузнечик». На чем он основывается, какова математика блочных криптоалгоритмов, а так же как реализуется данный алгоритм в java.

Кто, как, когда и зачем разработал данный алгоритм останется за рамками статьи, так как в данном случае нас это мало интересует, разве что:

КУЗНЕЧИК = КУЗнецов, НЕЧаев И Компания.

Так как криптография в первую очередь основана на математике, то чтобы дальнейшее объяснение не вызвало уймы вопросов сначала стоит разобрать базовые понятия и математические функции, на которых строится данный алгоритм.

Поля Галуа

Арифметика полей Галуа — полиномиальная арифметика, то есть каждый элемент данного поля представляет собой некий полином. Результат любой операции также является элементом данного поля. Конкретное поле Галуа состоит из фиксированного диапазона чисел.

Характеристикой поля называют некоторое простое число p. Порядок поля, т.е. количество его элементов, является некоторой натуральной степенью характеристики , где m ϵ N. При m=1 поле называется простым. В случаях, когда m>1, для образования поля необходим еще порождающий полином степени m, такое поле называется расширенным. – обозначение поля Галуа. Порождающий полином является неприводимым, то есть простым (по аналогии с простыми числами делится без остатка на 1 и на самого себя). Так как работа с любой информацией — это работа с байтами, а байт представляет из себя 8 бит, в качестве поля берут и порождающий полином:

Однако для начала разберем основные операции в более простом поле с порождающим полиномом .

Операция сложения

Самой простой является операция сложения, которая в арифметике полей Галуа является простым побитовым сложением по модулю 2 (ХОR).

Сразу обращаю внимание, что знак «+» здесь и далее по тексту обозначает операцию побитового XOR, а не сложение в привычном виде.

Таблица истинности функции ХОR

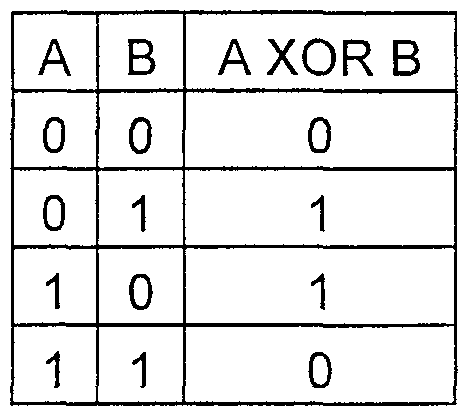
В полиномиальном виде данная операция будет выглядеть как

Операция умножения

Чтобы осуществить операцию умножения, необходимо преобразовать числа в полиномиальную форму:

Как можно заметить число в полиномиальной форме представляет собой многочлен, коэффициентами которого являются значения разрядов в двоичном представлении числа.

Перемножим два числа в полиномиальной форме:

Результат умножения 27 не входит в используемое поле (оно состоит из чисел от 0 до 7, как было сказано выше). Чтобы бороться с этой проблемой, необходимо использовать порождающий полином.

Также предполагается, что x удовлетворяет уравнению , тогда

Составим таблицу умножения:

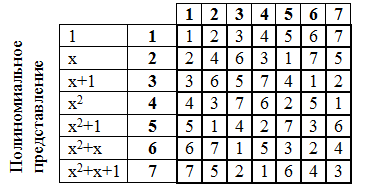
Большое значение имеет таблица степеней элементов поля Галуа. Возведение в степень также осуществляется в полиномиальной форме, аналогично умножению.

Таким образом, составим таблицу степеней:

Таблица степеней обладает цикличностью: седьмая степень соответствует нулевой, значит восьмая соответствует первой и т.д. При желании можно это проверить.

В полях Галуа существует понятие примитивного члена – элемент поля, чьи степени содержат все ненулевые элементы поля. Видно, что этому условию соответствуют все элементы (ну кроме 1, естественно). Однако это выполняется не всегда.

Для полей, которые мы рассматриваем, то есть с характеристикой 2, в качестве примитивного члена всегда выбирают 2. Учитывая его свойство, любой элемент поля можно выразить через степень примитивного члена.

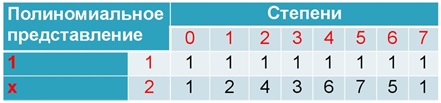
Воспользовавшись этим свойством, и учитывая цикличность таблицы степеней, попробуем снова перемножить числа:

Результат совпал с тем, что мы вычислили раньше.

А теперь выполним деление:

Полученный результат тоже соответствует действительности.

Ну и для полноты картины посмотрим на возведение в степень:

Такой подход к умножению и делению гораздо проще, чем реальные операции с использованием полиномов, и для них нет необходимости хранить большую таблицу умножения, а достаточно лишь строки степеней примитивного члена поля.

Теперь вернемся к нашему полю

Нулевой элемент поля — это единица, 1-й — двойка, каждый последующий со 2-го по 254-й элемент вычисляется как предыдущий, умноженный на 2, а если элемент выходит за рамки поля, то есть его значение больше чем , то делается XOR с числом , это число представляет неприводимый полином поля , приведем это число в рамки поля . А 255-ый элемент снова равен 1. Таким образом у нас есть поле, содержащее 256 элементов, то есть полный набор байт, и мы разобрали основные операции, которые выполняются в этом поле.

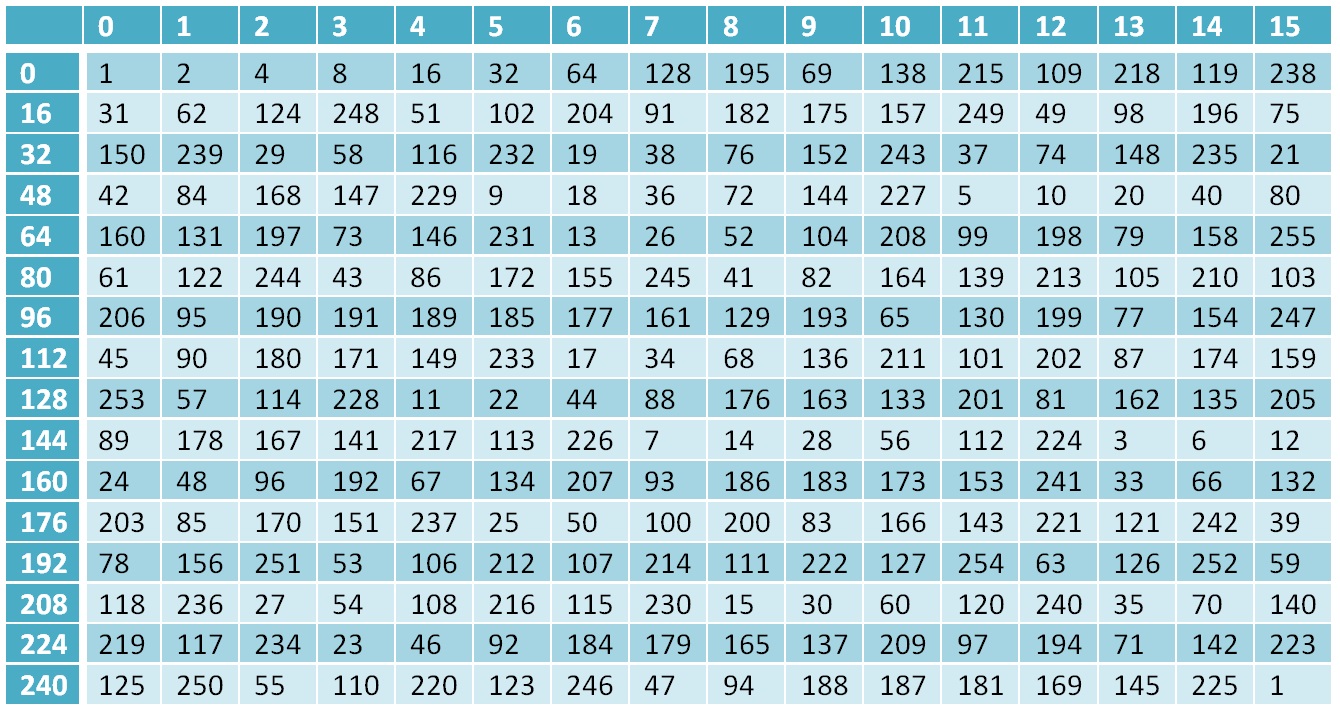
Таблица степеней двойки для поля

Для чего это было нужно — часть вычислений в алгоритме Кузнечик выполняются в поле Галуа, а результаты вычислений соответственно являются элементами данного поля.

Сеть Фейстеля

Сеть Фейстеля — это метод блочного шифрования, разработанный Хорстом Фейстелем в лаборатории IBM в 1971 году. Сегодня сеть Фейстеля лежит в основе большого количества криптографических протоколов.

Сеть Фейстеля оперирует блоками открытого текста:

1. Блок разбивается на две равные части — левую L и правую R.
2. Левый подблок L изменяется функцией f с использованием ключа K: X = f(L, K). В качестве функции может быть любое преобразование.
3. Полученный подблок X складывается по модулю 2 с правым подблоком R, который остался без изменений: X = X + R.
4. Полученные части меняются местами и склеиваются.

Рисунок 1. Ячейка Фейстеля

Сеть Фейстеля состоит из нескольких ячеек. Полученные на выходе первой ячейки подблоки поступают на вход второй ячейки, результирующие подблоки из второй ячейки попадают на вход третьей ячейки и так далее.

Алгоритм шифрования

Теперь мы познакомились с используемыми операциями и можем перейти к основной теме — а именно криптоалгоритму Кузнечик.

Основу алгоритма составляет так называемая SP сеть — подстановочно-перестановочная сеть (Substitution-Permutationnetwork). Шифр на основе SP-сети получает на вход блок и ключ и совершает несколько чередующихся раундов, состоящих из стадий подстановки и стадий перестановки. В «Кузнечике» выполняется девять полных раундов, каждый из которых включает в себя три последовательные операции:

1. Операция наложения раундового ключа или побитовый XOR ключа и входного блока данных;
2. Нелинейное преобразование, которое представляет собой простую замену одного байта на другой в соответствии с таблицей;
3. Линейное преобразование. Каждый байт из блока умножается в поле Галуа на один из коэффициентов ряда (148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1) в зависимости от порядкового номера байта (ряд представлен для порядковых номеров от 15-ого до 0-ого, как представлено на рисунке). Байты складываются между собой по модулю 2, и все 16 байт блока сдвигаются в сторону младшего разряда, а полученное число записывается на место считанного байта.

Последний десятый раунд не полный, он включает в себя только первую операцию XOR.

Кузнечик — блочный алгоритм, он работает с блоками данных длинной 128 бит или 16 байт. Длина ключа составляет 256 бит (32 байта).

Рисунок 2. Схема шифрования и расшифрования блока данных

На схеме показана последовательность операций, где S — нелинейное преобразование, L — линейное преобразование, Ki — раундовые ключи. Сразу возникает вопрос — откуда берутся раундовые ключи.

Формирование раундовых ключей

Итерационные (или раундовые) ключи получаются путем определенных преобразований на основе мастер-ключа, длина которого, как мы уже знаем, составляет 256 бит. Этот процесс начинается с разбиения мастер-ключа пополам, так получается первая пара раундовых ключей. Для генерации каждой последующей пары раундовых ключей применяется восемь итераций сети Фейстеля, в каждой итерации используется константа, которая вычисляется путем применения линейного преобразования алгоритма к значению номера итерации.

Схема получения итерационных (раундовых) ключей

Если вспомнить рисунок 1, то левый подблок L — левая половина исходного ключа, правый подблок R — правая половина исходного ключа, K — константа Ci, функция f — последовательность операций R XOR Ci, нелинейное преобразование, линейное преобразование.

Итерационные константы Ci получаются с помощью L-преобразования порядкового номера итерации.

Значит чтобы осуществить шифрование блока текста нам надо сначала рассчитать 32 итерационные константы, затем на основе ключа вычислить 10 раундовых ключей, и потом выполнить последовательность операций, представленных на рисунке 2.

Давайте начнем с вычисления констант:
Первая констант , однако все преобразования в нашем алгоритме выполняются с блоками длиной 16 байт, поэтому необходимо дополнить константу до длины блока, то есть дописать справа 15 нулевых байт, получим

Умножим ее на ряд (1, 148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148) следующим образом:

(данное равенство приведено в операциях полей Галуа)
Так как все кроме нулевого байта равны 0, а нулевой байт умножается на 1, то получим 1 и запишем его в старший разряд числа, сдвинув все байты в сторону младшего разряда, получим:

Повторим те же операции. На этот раз , все остальные байты 0, следовательно из слагаемых остается только первое , получаем:

Делаем третью итерацию, здесь два ненулевых слагаемых:

По таблице степеней можно было решить это гораздо проще:

Далее все точно также, всего 16 итераций на каждую константу

Источник: habr.com

Исполнители.Кузнечик

• Задание №5.1
• Посмотри внимательно. Уже на пятом шаге цикла КУЗНЕЧИК попал в точку 7, но вернулся назад в точку 5, еще 2 раза повторил команды и остановился в точке 7.

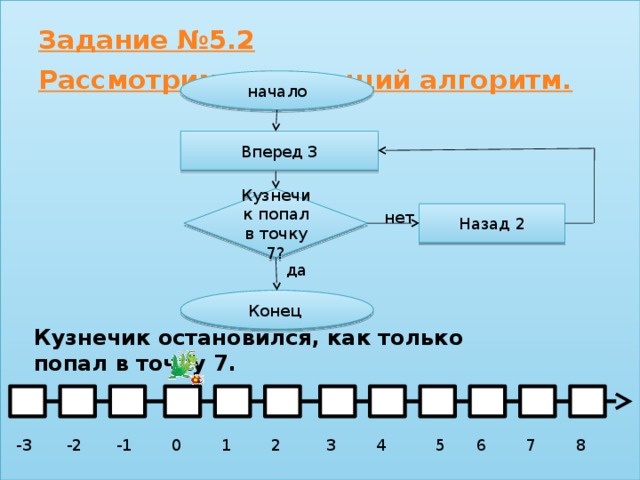
Задание №5.2 Рассмотрим следующий алгоритм.

Кузнечик попал в точку 7?

Кузнечик остановился, как только попал в точку 7.

Источник: videouroki.net