1 февраля 2023
Раздел BigInteger, подраздел Обычное Решение
public static BigInteger getFactorial(int f)
Разве здесь в 4-й строке метод valueOf(); не принимает long? Но i у нас имеет тип int, мы не можем его туда засунуть Пример взят один, но такое во всем разделе. Либо это я что-то путаю, проверьте меня
Екатерина Екатериновна Уровень 17
24 декабря 2022
А что за тетя на картинке, грустная такая, почему? На Лару Фабиан похожа, но постаревшую и уставшую.
Сергей Уровень 22
14 января 2022
«В Java часто для обработки чисел, особенно БОЛЬШИХ, используется класс BigInteger. Ведь если мы используем int, то максимальный факториал, который мы можем взять без потери данных, — 31, для long — 39. А что если нам нужен будет факториал 100?» Ведь максимальный факториал при int это 12! а long: 20!. Что за 31 и 39?) Решаю сейчас задачу и прочитав статью использовал значение 31. Изрядно намучался не понимая что не так)
5 января 2022
public class Factorial < public static void main(String[] args) throws IOException < String s = «543219»; // Любое число в виде строки. Здесь можно args[0], например Files.write( Paths.get(«factorial of » + s), Factorial(s).toString().getBytes()); // Вывод результата в файл >public static BigInteger Factorial(String targetNumberString) < BigInteger target = new BigInteger(targetNumberString).abs(); System.out.printf(«target: %s», target); if(!target.equals(BigInteger.ZERO)) < BigInteger factorial = target; while (!target.equals(BigInteger.ONE)) < target = target.subtract(BigInteger.ONE); System.out.printf(«nnext factor: %s», target); factorial = factorial.multiply(target); >return factorial; > return BigInteger.ONE; > >
Источник: javarush.com
Факториалы — это легко! Показываю, что это такое и как решать этот пример
Алгоритмы быстрого вычисления факториала
Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.
Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.
Наивный алгоритм
Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:
static BigInteger FactNaive(int n)
На моей машине эта реализация работает примерно 1,6 секунд для N=50 000.
Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.
Алгоритм вычисления деревом
Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.
Рекурсия. Факториал числа c++ рекурсивно. Рекурсия факториал. Рекурсивный алгоритм факториал. #44
Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R).
Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N).
Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10):
P(2, 10)
P(2, 6) * P(7, 10)
( P(2, 4) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( (P(2, 3) * P(4) ) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( ( (2 * 3) * (4) ) * (5 * 6) ) * ( (7 * 8) * (9 * 10) )
( ( 6 * 4 ) * 30 ) * ( 56 * 90 )
( 24 * 30 ) * ( 5 040 )
720 * 5 040
3 628 800
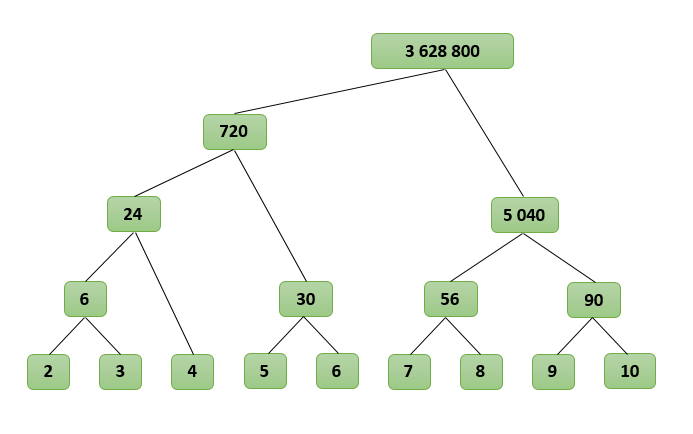
Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне
Реализуем описанный алгоритм:
static BigInteger ProdTree(int l, int r) < if (l >r) return 1; if (l == r) return l; if (r — l == 1) return (BigInteger)l * r; int m = (l + r) / 2; return ProdTree(l, m) * ProdTree(m + 1, r); > static BigInteger FactTree(int n)
Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации.
Алгоритм вычисления факторизацией
Второй алгоритм быстрого вычисления использует разложение факториала на простые множители (факторизацию). Очевидно, что в разложении N! участвуют только простые множители от 2 до N. Попробуем посчитать, сколько раз простой множитель K содержится в N!, то есть узнаем степень множителя K в разложении. Каждый K-ый член произведения 1 * 2 * 3 *… * N увеличивает показатель на единицу, то есть показатель степени будет равен N / K. Но каждый K 2 -ый член увеличивает степень еще на единицу, то есть показатель становится N / K + N / K 2 . Аналогично для K 3 , K 4 и так далее. В итоге получим, что показатель степени при простом множителе K будет равен N / K + N / K 2 + N / K 3 + N / K 4 +…
Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (2 2 ), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (2 3 ), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (2 4 ) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.
Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:
10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800
Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:
static BigInteger FactFactor(int n) < if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; bool[] u = new bool[n + 1]; // маркеры для решета Эратосфена List> p = new List>(); // множители и их показатели степеней for (int i = 2; i 0) < c += k; k /= i; >// запоминаем множитель и его показатель степени p.Add(new Tuple(i, c)); // просеиваем составные числа через решето int j = 2; while (i * j > // вычисляем факториал BigInteger r = 1; for (int i = p.Count() — 1; i >= 0; —i) r *= BigInteger.Pow(p[i].Item1, p[i].Item2); return r; >
Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000!
Библиотека GMP
Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP. Однако этому вопросу вероятно стоит посвятить отдельную статью.
Сравнение производительности
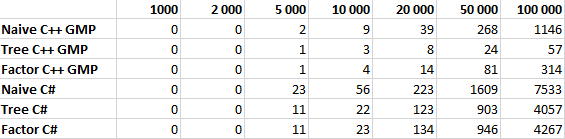
Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах.
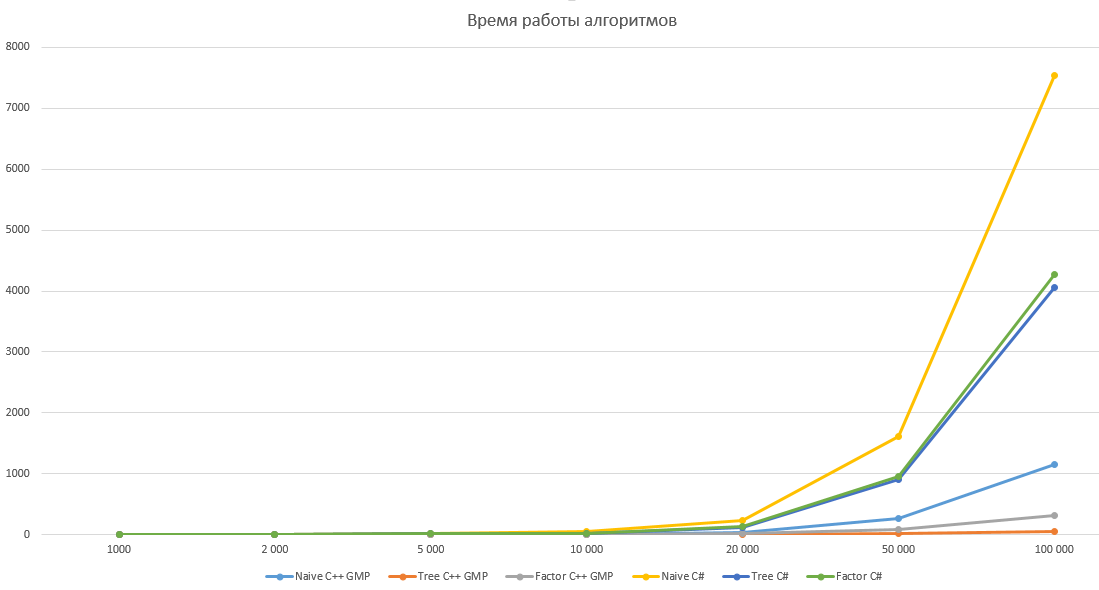
График с линейной шкалой
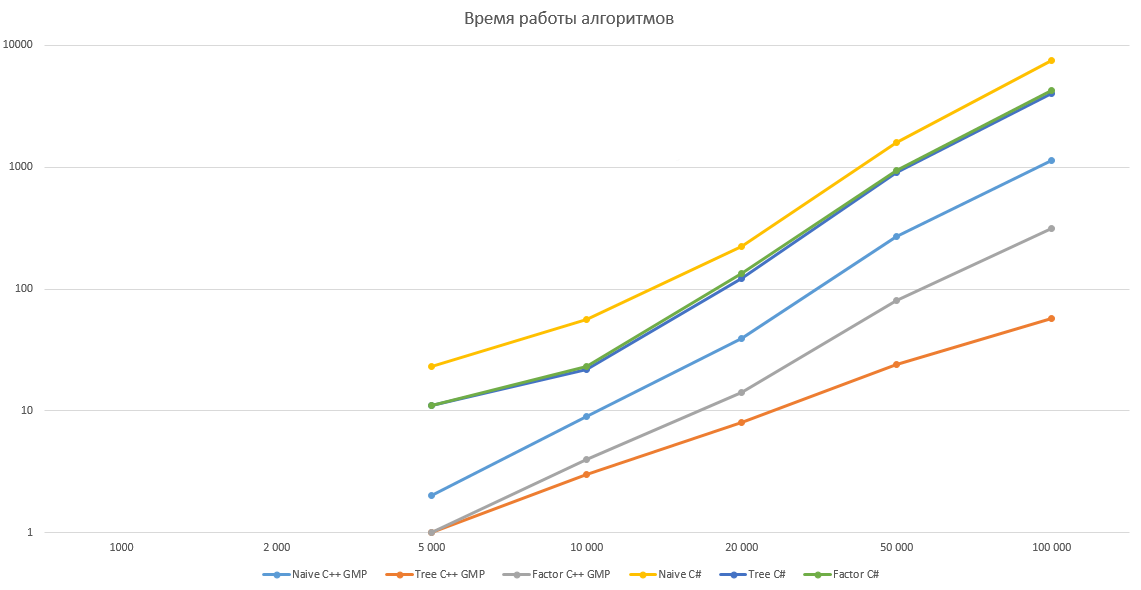
График с логарифмической шкалой
Идеи и алгоритмы из комментариев
Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них
Исходные коды
Исходные коды реализованных алгоритмов приведены под спойлерами
using System; using System.Linq; using System.Text; using System.Numerics; using System.Collections.Generic; using System.Collections.Specialized; namespace BigInt < class Program < static BigInteger FactNaive(int n) < BigInteger r = 1; for (int i = 2; i static BigInteger ProdTree(int l, int r) < if (l >r) return 1; if (l == r) return l; if (r — l == 1) return (BigInteger)l * r; int m = (l + r) / 2; return ProdTree(l, m) * ProdTree(m + 1, r); > static BigInteger FactTree(int n) < if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; return ProdTree(2, n); >static BigInteger FactFactor(int n) < if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; bool[] u = new bool[n + 1]; List> p = new List>(); for (int i = 2; i 0) < c += k; k /= i; >p.Add(new Tuple(i, c)); int j = 2; while (i * j > BigInteger r = 1; for (int i = p.Count() — 1; i >= 0; —i) r *= BigInteger.Pow(p[i].Item1, p[i].Item2); return r; > static void Main(string[] args) < int n; int t; Console.Write(«n = «); n = Convert.ToInt32(Console.ReadLine()); t = Environment.TickCount; BigInteger fn = FactNaive(n); Console.WriteLine(«Naive time: ms», Environment.TickCount — t); t = Environment.TickCount; BigInteger ft = FactTree(n); Console.WriteLine(«Tree time: ms», Environment.TickCount — t); t = Environment.TickCount; BigInteger ff = FactFactor(n); Console.WriteLine(«Factor time: ms», Environment.TickCount — t); Console.WriteLine(«Check: «, fn == ft ft == ff ? «ok» : «fail»); > > >
C++ с GMP
#include #include #include #include #include using namespace std; mpz_class FactNaive(int n) < mpz_class r = 1; for (int i = 2; i mpz_class ProdTree(int l, int r) < if (l >r) return 1; if (l == r) return l; if (r — l == 1) return (mpz_class)r * l; int m = (l + r) / 2; return ProdTree(l, m) * ProdTree(m + 1, r); > mpz_class FactTree(int n) < if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; return ProdTree(2, n); >mpz_class FactFactor(int n) < if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; vectoru(n + 1, false); vector > p; for (int i = 2; i 0) < c += k; k /= i; >p.push_back(make_pair(i, c)); int j = 2; while (i * j > mpz_class r = 1; for (int i = p.size() — 1; i >= 0; —i) < mpz_class w; mpz_pow_ui(w.get_mpz_t(), mpz_class(p[i].first).get_mpz_t(), p[i].second); r *= w; >return r; > mpz_class FactNative(int n) < mpz_class r; mpz_fac_ui(r.get_mpz_t(), n); return r; >int main() < int n; unsigned int t; cout
- длинная арифметика
- факториал
- оптимизация
Источник: habr.com
Итерационная программа для нахождения факториала числа
Напишите итеративную программу на C/C++ и Java, чтобы найти факториал заданного положительного числа.
The факториал неотрицательного целого числа n является произведением всех положительных целых чисел, меньших или равных n . Он обозначается n! . Факториал в основном используется для расчета общего количества способов, которыми n отдельные объекты могут быть организованы в последовательность.
The value of 5! is 120 as
5! = 1 × 2 × 3 × 4 × 5 = 120
(5 distinct objects can be arranged into a sequence in 120 ways).
The value of 0! is 1
В итеративной версии используется цикл для вычисления произведения всех положительных целых чисел, меньших, чем равных n . Поскольку факториал числа может быть огромным, тип данных факториальной переменной объявляется как unsigned long .
Реализацию можно увидеть ниже на C, Java и Python:
Источник: www.techiedelight.com