В этом уроке мы обсудим, как мы можем преобразовать десятичное число в двоичное, восьмеричное и шестнадцатеричное числа в Python.
Наиболее широко используемой системой счисления является десятичная система. Она является системой счисления с основанием 10. В этой системе десять цифр (0-9) используются для представления числа.
Двоичная система – это система счисления с основанием 2. Двоичная система используется потому, что компьютеры понимают только двоичные числа (0 и 1).
Восьмеричная система – это система счисления с основанием 8.
Шестнадцатеричная система – это система счисления с основанием 16.
У нас есть десятичное число, и мы в нашей программе должны преобразовать его в двоичное, восьмеричное и шестнадцатеричное число. Мы будем использовать функцию для преобразования десятичных чисел в двоичные числа, восьмеричные числа и в шестнадцатеричные числа.
Input: 64 Output: 64 in Binary: 0b1000000 64 in Octal: 0o100 64 in Hexadecimal: 0x40 Input: 312 Output: 312 in Binary: 0b100111000 312 in Octal: 0o470 312 in Hexadecimal: 0x138
# First, we will define the function to convert decimal to binary def decimal_into_binary(decimal_1): decimal = int(decimal_1) # then, print the equivalent decimal print(«The given decimal number», decimal, «in Binary number is: «, bin(decimal)) # we will define the function to convert decimal to octal def decimal_into_octal(decimal_1): decimal = int(decimal_1) # Then, print the equivalent decimal print(«The given decimal number», decimal, «in Octal number is: «, oct(decimal)) # we will define the function to convert decimal to hexadecimal def decimal_into_hexadecimal(decimal_1): decimal = int(decimal_1) # Then, print the equivalent decimal print(«The given decimal number», decimal, » in Hexadecimal number is: «, hex(decimal)) # Driver program decimal_1 = int(input(» Enter the Decimal Number: «)) decimal_into_binary(decimal_1) decimal_into_octal(decimal_1) decimal_into_hexadecimal(decimal_1)
Enter the Decimal Number: 12 The given decimal number 12 in Binary number is: 0b1100 The given decimal number 12 in Octal number is: 0o14 The given decimal number 12 in Hexadecimal number is: 0xc
Enter the Decimal Number: 196 The given decimal number 196 in Binary number is: 0b11000100 The given decimal number 196 in Octal number is: 0o304 The given decimal number 196 in Hexadecimal number is: 0xc4
Перевод из десятичной в двоичную систему счисления
В приведенной выше программе мы использовали встроенные функции: bin() (для двоичного), oct() (для восьмеричного) и hex() (для шестнадцатеричного) для преобразования данного десятичного числа в соответствующие системы счисления. Эти функции принимают целое число и возвращают строку.
Заключение
В этом руководстве мы обсудили, как мы можем использовать встроенные функции Python для преобразования десятичных чисел в двоичные, восьмеричные и шестнадцатеричные числа.
Источник: pythonpip.ru
Перевод числа в двоичную систему за два шага!!!
Упражнения на C: преобразование десятичного числа в двоичное
Напишите программу на C для преобразования десятичного числа в двоичное с использованием рекурсии.
Иллюстрированная презентация:

Пример решения:
Код C:
#include long convertBinary(int); int main() < long biNo; int decNo; printf(«nn Recursion : Convert decimal number to binary :n»); printf(«—————————————————n»); printf(» Input any decimal number : «); scanf(«%d», biNo = convertBinary(decNo);//call the function convertBinary printf(» The Binary value of decimal no. %d is : %ldnn»,decNo,biNo); return 0; >long convertBinary(int decNo) < static long biNo,r,fctor = 1; if(decNo != 0) < r = decNo % 2; biNo = biNo + r * fctor; fctor = fctor * 10; convertBinary(decNo / 2);//calling the function convertBinary itself recursively >return biNo; >
Рекурсия: преобразование десятичного числа в двоичное: ————————————————— — Введите любое десятичное число: 66 Двоичное значение десятичного числа нет. 66 это: 1000010
Блок — схема:

Редактор кода программирования C:
Есть другой способ решить это решение? Внесите свой код (и комментарии) через Disqus.
Источник: www.kodesource.top
Как преобразовать десятичное число в двоичное в Python.

Простой способ преобразования десятичной системы счисления в двоичную в Python заключается в последовательном делении десятичного числа на 2 и сохранении модуля, остатка или остатка каждого деления до тех пор, пока вы не получите ноль в значении коэффициента. Наконец, все модули соединяются в обратном порядке, чтобы получить число в двоичном виде.
Чтобы лучше понять это, достаточно увидеть это на картинке:
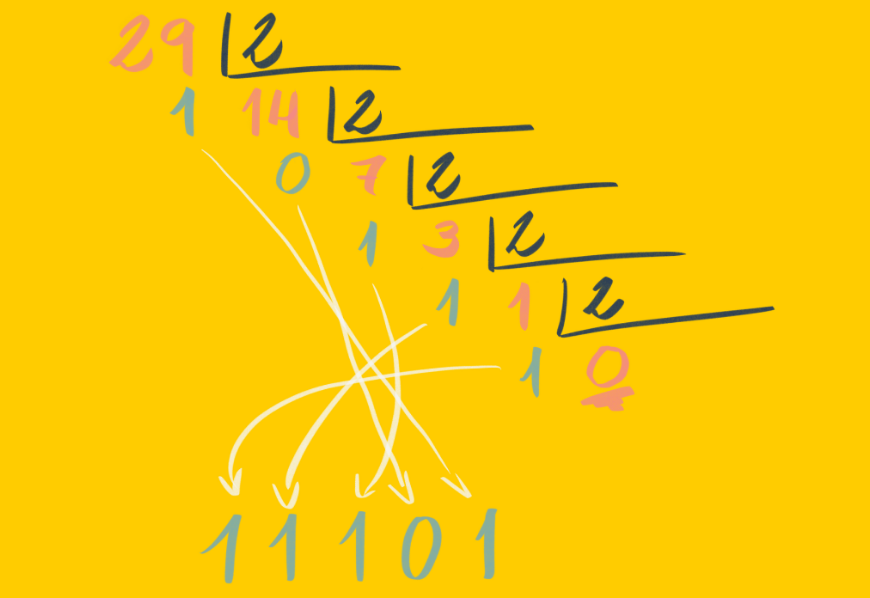
На самом деле это математический способ решения данной проблемы. Вы можете сделать это так независимо от используемого языка. То есть, это общий алгоритм преобразования десятичного числа в его двоичный эквивалент.
Давайте теперь посмотрим, как реализовать этот алгоритм в Python.
Шаг 1: Выполните целочисленное деление десятичного числа на 2
Первый шаг, очень простой, является основополагающим, и нам придется повторять его в цикле, чтобы получить желаемое число. Но давайте не будем забегать вперед.
Речь идет о делении исходного числа на 2. Кроме того, нам понадобятся два различных числа, получающихся в результате деления: коэффициент и модуль (также называемый остатком).
Вот почему мы должны использовать целочисленное деление, стандартное деление не годится.
В Python 3 символом целочисленного деления является двойная косая черта //. Если вы примените одинарную косую черту /, вы получите фактический результат деления, и он не будет работать, потому что вам нужно отдельно получить коэффициент и модуль.
Выполняя целочисленное деление с двойной косой чертой, вы получите коэффициент. Рассмотрим несколько примеров.
>>> 10 // 4 2 >>> 6 // 3 2 >>> 15 // 2 7 Code language: JavaScript (javascript)
Как я уже говорил, нам также нужно получить модуль, поэтому применяем оператор %, который снова отвечает за решение целочисленного деления, но на этот раз результатом будет модуль.
Рассмотрим те же примеры:
>>> 10 % 4 2 >>> 6 % 3 0 >>> 15 % 2 1
Благодаря этому у нас есть все необходимые элементы. Мы можем проверить их правильность с помощью типичного теста на деление, которому нас учили в школе: “делимое равно делитель умножить на делитель плюс остаток”.
>>> 10 == 5 * (10 // 5) + (10 % 5) True >>> 6 == 3 * (6 // 3) + (6 % 3) True >>> 15 == 2 * (15 // 2) + (15 % 2) TrueCode language: PHP (php)
Шаг 2: Сохраняем модуль деления на 2
На втором этапе необходимо сохранить модуль, полученный в предыдущем пункте. Поскольку это итеративный процесс, в котором мы собираемся сохранить несколько модулей, лучше всего создать список и хранить их в нем.
Достаточно создать пустой список под названием, например, modules и добавить в конец только что вычисленный модуль m с помощью функции append следующим образом: modules.append(m).
Шаг 3: Повторяем шаги 1 и 2, пока коэффициент не будет равен 0.
Как я уже говорил, это итеративный процесс, поэтому нам нужно выполнить шаги 1 и 2 в цикле, помня о двух основных моментах:
- Каждый раз, когда мы получаем коэффициент, он становится числом, которое мы используем в следующей итерации для выполнения деления.
- Необходимо остановить цикл, когда полученный коэффициент будет равен 0. Больше смысла продолжать не имеет делить 0 на 2.
Этот итерационный процесс получает на вход число, которое мы хотим преобразовать в двоичный формат. Это число делится на 2, чтобы получить коэффициент. Этот коэффициент становится входным числом в следующей операции. Таким образом, число становится все меньше и меньше, пока, наконец, не станет нулем. В этот момент мы останавливаем цикл.
Посмотрите еще раз на изображение выше, чтобы не запутаться.
Давайте посмотрим, как выглядит код:
decimal_number = 29 # это число, которое мы хотим перевести в двоичный формат modules = [] # список для хранения модулей while decimal_number != 0: # делаем, пока входное число отлично от нуля # шаг 1: деление на 2 module = decimal_number % 2 quotient = decimal_number // 2 modules.append(module) # сохраняем вычисленный модуль decimal_number = cociente # коэффициент становится входным числом print(modules)Code language: PHP (php)
Таким образом, результат, где видны рассчитанные модули, выглядит так:
[1, 0, 1, 1, 1]Code language: JSON / JSON with Comments (json)
Перепишем код, потому что для вашего понимания я написал его шаг за шагом, но его можно еще немного оптимизировать следующим образом:
decimal_number = 29 # это число, которое мы хотим перевести в двоичный формат modules = [] # список для хранения модулей while decimal_number != 0: # делаем, пока входное число отлично от нуля modules.append(decimal_number % 2) # получение и хранение модуля decimal_number //= 2 # коэффициент становится входным числомCode language: PHP (php)
Шаг 4: Перевернем сохраненные модули
После получения модулей их необходимо развернуть, так как результирующее двоичное число состоит из всех этих конкатенированных модулей, но в порядке, обратном тому, в котором они были получены. Это можно сделать очень просто, используя порционную нотацию для получения всего списка в обратном порядке следующим образом: modules = modules[::-1].
Однако эта операция не нужна, если, когда нам нужно сохранить новый вычисленный модуль в списке, мы сохраняем его в начале списка, а не в конце. Таким образом, он уже непосредственно инвертирован, что является тем порядком, который нам нужен.
Для этого мы можем воспользоваться функцией insert, которая позволяет вставить элемент в список, но в нужную нам позицию. Если мы всегда вставляем модуль в позицию 0, этот элемент становится первым в списке, сдвигая все остальные на одну позицию вправо.
Функция insert требует двух параметров, первый из которых – позиция или индекс, куда мы хотим вставить новый элемент, а второй – сам элемент:
>>> list = [] >>> list.insert(0, 1) >>> list.insert(0, 2) >>> list.insert(0, 3) >>> print(list) [3, 2, 1]Code language: PHP (php)
Давайте адаптируем наш код, чтобы хранить модули в правильном порядке:
decimal_number = 29 modules = [] while decimal_number != 0: # модуль сохраняется в правильном порядке modules.insert(0, decimal_number % 2) decimal_number //= 2 print(modules)Code language: PHP (php)
Результат будет таким:
[1, 1, 1, 0, 1]Code language: JSON / JSON with Comments (json)
Шаг 5: Объединение модулей для получения окончательного двоичного числа
Обратите внимание, что при получении модулей деления на 2 результат каждого модуля всегда равен 0 или 1, так как это возможные остатки от деления на 2. Таким образом, получение конечного двоичного числа уже очень просто.
Теперь остается только объединить все числа, чтобы получить окончательное двоичное число.
Существует несколько способов выполнения этой операции:
- Математически мы можем умножить каждую цифру на 10 в ее позиции и сложить все результаты. Таким образом, число, соответствующее единицам, умножается на 10 с точностью до 0, десяткам – на 10 с точностью до 1, сотням – на 10 с точностью до 2 и так далее.
- Если мы преобразуем цифры в символ и выполним операцию объединения следующим образом: ”.join(modules) останется только преобразовать число в целое (если захотим) с помощью функции int: int(”.join(modules)).
Я предпочитаю применять математику, но с небольшой оптимизацией: почему бы не создавать новое двоичное число с каждым вычисленным модулем вместо того, чтобы хранить его в списке, который нам нужно обработать позже? Для этого я немного изменил код, который уже есть в цикле для генерации неполного двоичного числа.
decimal_number = 29 binary_number = 0 multiplier = 1 while decimal_number != 0: # шаг 3 # шаги 1, 4 и 5 умножение модуля на его множитель binary_number = binary_number + decimal_number % 2 * multiplier decimal_number //= 2 # шаг 1 multiplier *= 10 # шаг 5 print(binary_number)Code language: PHP (php)
Как видите, нам уже удалось получить номер. Правда, список нам больше не нужен, но нам нужно знать позицию каждой цифры, чтобы умножить ее на 10 . Поскольку эти значения равны 1, 10, 100, 1000 и т.д. соответственно для позиций 0, 1, 2, 3 и т.д., все, что нам нужно сделать, это использовать переменную множителя, начинающуюся с 1, и умножать ее на 10 на каждой итерации. Мы будем использовать эту переменную для умножения на вычисленный модуль и прибавления результата к двоичному числу.
Результат этого кода – 11101, что в двоичном исчислении составляет ровно 29.
Шаг 6 (необязательный): заключиyие алгоритма в функцию преобразования десятичной системы в двоичную.
Вот и все, осталось только создать функцию с этим кодом для преобразования любого десятичного числа в двоичное. Это удобно, если вам нужно выполнить эту операцию несколько раз в вашем коде.
def decimal_to_binary(decimal_number): binary_number = 0 multiplier = 1 while decimal_number != 0: # шаги 1, 4 и 5 умножение модуля на его множитель binary_number = binary_number + decimal_number % 2 * multiplier decimal_number //= 2 multiplier *= 10 return binary_number # примеры использования print(decimal_to_binary(5)) print(decimal_to_binary(35)) print(decimal_to_binary(22301))Code language: PHP (php)
В результате мы получим следующие двоичные числа на экране:
101 100011 101011100011101
Альтернативный вариант
То, что я рассказал вам в этой статье, представляет интерес, если вы действительно изучаете Python и хотите разобраться, как выполнить эту операцию с помощью алгоритма.
Если нет и вам нужен быстрый способ преобразования десятичного числа в двоичное, Python предоставляет функцию bin, которая, задав десятичное число, возвращает его эквивалент в двоичном виде. Однако в текстовом формате и с префиксом 0b, обозначающим двоичное число:
>>> bin(29) ‘0b11101’ >>> bin(5) ‘0b101’ >>> bin(14) ‘0b1110’Code language: JavaScript (javascript)
Источник: dvsemenov.ru