Есть ли в Python библиотечная функция, которая может перечислять простые числа (последовательно)? Я нашел этот вопрос Самый быстрый способ перечислить все простые числа ниже N, но я предпочитаю использовать чью-то надежную библиотеку, чем создавать собственную. Я был бы рад сделать import math; for n in math.primes:
person Colonel Panic schedule 10.11.2012 source источник
Вопрос, на который вы ссылаетесь, имеет ссылку на библиотеку numpy, которая имеет функцию простых чисел . — person Hunter McMillen nbsp schedule 11.11.2012
вам всегда придется устанавливать верхний предел N . и для большого значения N это может занять много времени . — person Joran Beasley nbsp schedule 11.11.2012
Ответы (4)
Другой вариант — SymPy. Это библиотека Python для символической математики. Он предоставляет несколько функций для прайма.
isprime(n) # Test if n is a prime number (True) or not (False). primerange(a, b) # Generate a list of all prime numbers in the range [a, b). randprime(a, b) # Return a random prime number in the range [a, b). primepi(n) # Return the number of prime numbers less than or equal to n. prime(nth) # Return the nth prime, with the primes indexed as prime(1) = 2. The nth prime is approximately n*log(n) and can never be larger than 2**n. prevprime(n, ith=1) # Return the largest prime smaller than n nextprime(n) # Return the ith prime greater than n sieve.primerange(a, b) # Generate all prime numbers in the range [a, b), implemented as a dynamically growing sieve of Eratosthenes.
Вот несколько примеров.
>>> import sympy >>> >>> sympy.isprime(5) True >>> list(sympy.primerange(0, 100)) [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97] >>> sympy.randprime(0, 100) 83 >>> sympy.randprime(0, 100) 41 >>> sympy.prime(3) 5 >>> sympy.prevprime(50) 47 >>> sympy.nextprime(50) 53 >>> list(sympy.sieve.primerange(0, 100)) [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
person SparkAndShine schedule 24.02.2017
Решето Эратосфена – алгоритм определения простых чисел. Решение задачи на Python
Библиотека gmpy2 имеет функцию next_prime (). Эта простая функция создаст генератор, который обеспечит бесконечный запас простых чисел:
import gmpy2 def primes(): n = 2 while True: yield n n = gmpy2.next_prime(n)
Если вы будете многократно перебирать простые числа, создание и повторное использование таблицы всех простых чисел ниже разумного предела (скажем, 1000000) будет быстрее. Вот еще один пример использования gmpy2 и решета Эратосфена для создания таблицы простых чисел. primes2 () сначала возвращает простые числа из таблицы, а затем использует next_prime ().
import gmpy2 def primes2(table=None): def sieve(limit): sieve_limit = gmpy2.isqrt(limit) + 1 limit += 1 bitmap = gmpy2.xmpz(3) bitmap[4 : limit : 2] = -1 for p in bitmap.iter_clear(3, sieve_limit): bitmap[p*p : limit : p+p] = -1 return bitmap table_limit=1000000 if table is None: table = sieve(table_limit) for n in table.iter_clear(2, table_limit): yield n n = table_limit while True: n = gmpy2.next_prime(n) yield n
Вы можете настроить table_limit в соответствии со своими потребностями. Большие значения потребуют больше памяти и увеличат время запуска для первого вызова primes (), но это будет быстрее для повторных вызовов. Примечание: я сопровождаю gmpy2.
Простые числа (Python)
person casevh schedule 11.11.2012
В документации для gmpy2 сказано: next_prime (x) возвращает следующее вероятное простое число ›x. Текст, выделенный жирным шрифтом в соответствии с документом. Я думаю, что это нужно прояснить. — person Dave Rove; 18.09.2018
Задав этот вопрос, я написал оболочку Python вокруг primesieve библиотеки C ++, которая впоследствии была принята сопровождающим primesieve. https://github.com/kimwalisch/primesieve-python
>>> from primesieve import * # Generate a list of the primes below 40 >>> generate_primes(40) [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37] # Generate a list of the primes between 100 and 120 >>> generate_primes(100, 120) [101, 103, 107, 109, 113] # Generate a list of the first 10 primes >>> generate_n_primes(10) [2, 3, 5, 7, 11, 13, 17, 19, 23, 29] # Generate a list of the first 10 starting at 1000 >>> generate_n_primes(10, 1000) [1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061] # Get the 10th prime >>> nth_prime(10) 29 # Count the primes below 10**9 >>> count_primes(10**9) 50847534
person Colonel Panic schedule 10.11.2015
Не существует алгоритма постоянного времени для генерации следующего простого числа; вот почему для большинства библиотек требуется верхняя граница. На самом деле это огромная проблема, которую необходимо было решить для цифровой криптографии. RSA выбирает достаточно большие простые числа, выбирая случайное число и проверяя простоту, пока не найдет простое число. Учитывая произвольное целое число N , единственный способ найти следующее простое число после N — это пройти через N+1 до неизвестного простого P , проверяя простоту. Тестирование на простоту очень дешево, и для этого существуют библиотеки Python: алгоритм AKS Primes в Python Для функции test_prime итератор с бесконечным числом простых чисел будет выглядеть примерно так:
class IterPrimes(object): def __init__(self,n=1): self.n=n def __iter__(self): return self def next(self): n = self.n while not test_prime(n): n += 1 self.n = n+1 return n
Есть много эвристик, которые можно использовать для ускорения процесса. Например, пропускайте четные числа или числа, делящиеся на 2, 3, 5, 7, 11, 13 и т. Д.
Источник: questu.ru
Загадки Python — Генерация простых чисел!
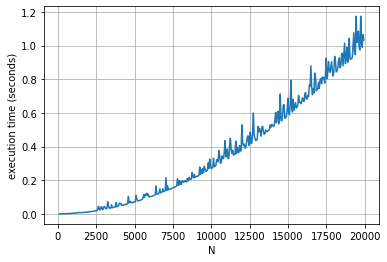
Обычно существует несколько способов решения задач даже пограничной сложности. Как же определить оптимальное и эффективное решение?
В этой статье мы представим достаточно простую задачу с несколькими решениями, чтобы показать, как думать и оценивать оптимизацию вычислительной сложности. Оптимизацию памяти мы обсудим в другой статье, возможно, на другом примере.
ПОСТАНОВКА ЗАДАЧИ
Давайте обратимся к одной из фундаментальных проблем математики: определение и генерация набора простых чисел меньше заданного целого числа. Ваша задача — создать эффективный метод (как алгоритмически, так и программно) для оптимизации вычислительных ресурсов.
Математическое определение:
Простое число определяется как любое положительное целое число больше 1, которое не делится ни на какое целое число, кроме 1 и самого себя.
Входной аргумент:
N = 35 (используется в качестве примера)
Ожидаемый результат:
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31]
Ограничения:
Нет. Однако обсудите различные методы оптимизации.
РЕШЕНИЕ
Задача — Посчитать количество простых чисел — программирование на разных языках

Задача — Посчитать количество простых чисел
— программирование на Pascal, Си, Кумир, Basic-256, Python
Вводятся десять натуральных чисел больше 2. Посчитать, сколько среди них простых чисел.
Простым называется натуральное число (кроме 1), делителями которого являются только оно само и 1. Например, число 5 — простое, т.к. его можно нацело разделить только на 5 и 1, а число 6 — сложное, т.к. помимо 6 и 1 делится на 2 и 3.
- Предположим изначально, что все десять чисел простые. Присвоим счетчику простых чисел значение 10.
- Каждое вводимое число надо проверить на делимость на все натуральные числа начиная с двойки и до квадратного корня до него.
- Если хотя бы один из делителей делит число нацело, значит число сложное и надо уменьшить счетчик простых чисел.
- В конце программы вывести значение счетчика простых чисел. Оно будет уменьшено на количество введенных сложных чисел, следовательно, будет показывать количество введенных простых чисел.
Pascal
var
count, i: byte;
n, j: word;
begin
count := 10;
for i:=1 to 10 do begin
read(n);
for j:=2 to trunc(sqrt(n))+1 do
if n mod j = 0 then begin
count := count — 1;
break;
end;
end;
writeln(‘Простых чисел ‘, count);
end. 15 16 17 18 19 20
21 22 23 24 25
Простых чисел 3
Язык Си
main() unsigned int n, count, i, j;
count = 10;
for (i=0; i <10; i++) scanf(«%d»,
for (j=2; j if (n%j == 0) count -= 1;
break;
>
>
printf(«Простых чисел: %dn», count);
> 5
6
7
8
9
10
11
12
13
14
Простых чисел: 4
При gcc использовать ключ -lm.
Python
from math import sqrt
count = 10
for i in range(10):
n = int(input())
for j in range(2, int(sqrt(n))+1):
if n%j == 0:
count -= 1
break
print(count) 13
4
12
30
18
11
23
100
113
997
Количество простых чисел: 5
КуМир
алг простые числа
нач
цел count, i, n, j
count := 10;
нц для i от 1 до 10
ввод n
нц для j от 2 до int(sqrt(n))+1
если mod(n,j) = 0 то
count := count — 1
выход
все
кц
кц
вывод «Простых чисел «, count
кон 78
113
101
107
45
110
118
121
201
501
Простых чисел 3
Basic-256
c = 10
for i=1 to 10
input n
for j=2 to (int(sqrt(n))+1)
if n%j = 0 then
c = c — 1
goto go
endif
next j
go:
next i
print «Простых чисел: » + c 100
101
102
103
104
105
106
107
108
109
Простых чисел: 4
Источник: ars-games.ru