Матрицы являются одним из основных объектов в математике. Они используются для представления и манипулирования данными в виде таблицы, состоящей из строк и столбцов. Их используют для решения систем линейных уравнений, определения матричных действий, преобразования координат и многого другое.
В этой статье мы опишем несколько способов создать матрицу в Python. И дополнительно рассмотрим некоторые основные операции, такие как сложение, умножение и определение обратной матрицы.
Что такое матрица
Матрица — это таблица из чисел, которая используется в математике и инженерных науках для представления данных. Матрицы имеют форму таблицы, состоящей из строк и столбцов. Каждый элемент имеет свой уникальный индекс, обозначающий строку и столбец, в котором он находится. Например, матрица размером 3×3 будет иметь 3 строки и 3 столбца, и каждый элемент будет иметь индекс вида (i, j), где i — номер строки, а j — номер столбца.
Создание матрицы
В Python существует несколько способов создания матрицы. Ниже приведены некоторые из них:
«Магические способности в матрице судьбы» — Magic Market онлайн — апрель-2020
- С помощью списков. Можно создать матрицу, используя вложенные списки. Каждый вложенный список будет соответствовать одной строке. Так можно создать квадратную матрицу Python :
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
- С помощью NumPy. NumPy — это библиотека для математических вычислений и обработки данных. В ней есть класс Array, который можно использовать для создания матрицы:
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
Если вам нужно производить стандартные математические операции с матрицами, то стоит использовать NumPy. Его проще использовать и все операции уже реализованы в библиотеке. А если вы хотите самостоятельно создавать методы, например, в образовательных целях, или же планируете совершать нестандартные манипуляции, то используйте вложенные списки.
Теперь рассмотрим матричные операции и поработаем с ними с помощью вложенных списков и NumPy.
Матричные операции
Вот список основных манипуляций:
- Сложение. Две матрицы можно сложить, если их размеры совпадают. Каждый элемент итоговой матрицы будет равен сумме соответствующих элементов исходных матриц.
- Вычитание. Одну матрицу можно вычесть из другой, если их размеры совпадают. Каждый элемент итоговой матрицы будет равен разности соответствующих элементов исходных матриц.
- Умножение начисло. Каждый элемент итоговой матрицы будет равен произведению соответствующего элемента исходной матрицы на число.
- Произведение матриц. Матрицы можно перемножить, если число столбцов первой матрицы равно числу строк второй матрицы. В результате получится новая матрица с размером, соответствующим числу строк первой матрицы и числу столбцов второй матрицы. Более подробно эту операцию мы разберем чуть дальше.
- Транспонирование матрицы. Транспонирование — это операция, в которой строки и столбцы меняются местами. Т.е. первый столбец становится первой строкой, второй столбец — второй строкой и так далее.
- Нахождение обратной матрицы. Матрица B будет являться обратной матрицей для матрицы A, если результатом операции A*B является единичная матрица.
Сложение
Важно не забывать, что при сложении двух матриц их размеры должны совпадать.
Программы в матрице. Кармические хвосты. Матрица судьбы
Вот пример сложения с помощью вложенных списков и циклов:
matrix1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
matrix2 = [[9, 8, 7], [6, 5, 4], [3, 2, 1]]
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for i in range(len(matrix1)):
for j in range(len(matrix1[0])):
result[i][j] = matrix1[i][j] + matrix2[i][j]
print(result)
[[10, 10, 10], [10, 10, 10], [10, 10, 10]]
Вот аналогичное сложение с помощью метода add() из библиотеки NumPy:
import numpy as np
matrix1 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
matrix2 = np.array([[9, 8, 7], [6, 5, 4], [3, 2, 1]])
result = np.add(matrix1, matrix2)
print(result)
[[10 10 10]
[10 10 10]
[10 10 10]]
Вычитание
В Python можно выполнять вычитание матриц с помощью цикла или метода subtract() из библиотеки NumPy. При вычитании размеры должны совпадать.
Вычитание с помощью цикла:
matrix1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
matrix2 = [[9, 8, 7], [6, 5, 4], [3, 2, 1]]
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for i in range(len(matrix1)):
for j in range(len(matrix1[0])):
result[i][j] = matrix1[i][j] — matrix2[i][j]
print(result)
[[-8, -6, -4], [-2, 0, 2], [4, 6, 8]]
Вычитание с помощью метода subtract() из библиотеки NumPy:
import numpy as np
matrix1 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
matrix2 = np.array([[9, 8, 7], [6, 5, 4], [3, 2, 1]])
result = np.subtract(matrix1, matrix2)
print(result)
[[-8 -6 -4]
[-2 0 2]
[ 4 6 8]]
Умножение на число
В Python умножение матрицы на число можно реализовать с помощью цикла или воспользоваться методом dot() из библиотеки NumPy.
При умножении матрицы на число, каждый элемент умножается на это число.
Умножение с помощью цикла:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
scalar = 2
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for i in range(len(matrix)):
for j in range(len(matrix[0])):
result[i][j] = matrix[i][j] * scalar
print(result)
[[2, 4, 6], [8, 10, 12], [14, 16, 18]]
Вот пример работы метода dot() из библиотеки NumPy с теми же вводными:
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
scalar = 2
result = np.dot(matrix, scalar)
print(result)
[[ 2 4 6]
[ 8 10 12]
[14 16 18]]
Также вместо метода dot() можно использовать знак операции умножения * :
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
scalar = 2
result = matrix * scalar
print(result)
[[ 2 4 6]
[ 8 10 12]
[14 16 18]]
В большинстве случаев метод dot() работает быстрее вручную реализованных циклов.
Произведение матриц
Произведение — это операция, в результате которой получается новая матрица с числом строк первой матрицы и числом столбцов второй. При матричном умножении, число столбцов первой матрицы должно совпадать с числом строк второй. Каждый элемент новой матрицы — это сумма произведения элементов строки первой матрицы и элементов столбцов второй матрицы, как на картинке ниже:
Как и прежде, реализуем произведение с помощью циклов и NumPy.
Умножение, реализованное на циклах, может иметь такой вид:
matrix1 = [[1, 2], [3, 4]]
matrix2 = [[5, 6], [7, 8]]
result = [[0, 0], [0, 0]]
for i in range(len(matrix1)):
for j in range(len(matrix2[0])):
for k in range(len(matrix2)): result[i][j] += matrix1[i][k] * matrix2[k][j]
print(result)
[[19, 22], [43, 50]]
В NumPy для матричного умножения используется метода dot() :
import numpy as np
matrix1 = np.array([[1, 2], [3, 4]])
matrix2 = np.array([[5, 6], [7, 8]])
result = np.dot(matrix1, matrix2)
print(result)
[[19 22]
[43 50]]
[[19 22]
[43 50]]
Не забывайте, что произведение является некоммутативной операцией, то есть порядок умножения матриц имеет значение и результат будет разным, если их переставить местами.
Транспонирование
Транспонирование — это операция, в результате которой строки исходной матрицы становятся столбцами новой матрицы, а столбцы — строками.
В Python можно выполнить транспонирование с помощью свойства T или метода transpose() из библиотеки NumPy .
Пример транспонирования с использованием свойства T :
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
result = matrix.T
print(result)
[[1 4 7]
[2 5 8]
[3 6 9]]
И пример транспонирования с использованием метода transpose() :
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
result = np.transpose(matrix)
print(result)
[[1 4 7]
[2 5 8]
[3 6 9]]
В обоих случаях результат одинаковый.
С помощью цикла транспонирование можно реализовать следующим образом:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for i in range(len(matrix)):
for j in range(len(matrix[0])):
result[j][i] = matrix[i][j]
print(result)
[[1, 4, 7], [2, 5, 8], [3, 6, 9]]
Этот метод может быть медленным и неэффективным для больших матриц, поэтому для более быстрого и эффективного решения рекомендуется использовать NumPy.
Нахождение обратной матрицы
Обратная матрица — это матрица, которая при умножении на исходную матрицу в результате дает единичную матрицу (с единицами на диагонали и нулями в остальных ячейках).
В Python можно найти обратную матрицу с помощью метода inv() из библиотеки NumPy.
import numpy as np
matrix = np.array([[1, 2], [3, 4]])
result = np.linalg.inv(matrix)
print(result)
[[-2. 1. ]
[ 1.5 -0.5]]
Если матрица не имеет обратной матрицы, то метод inv() вызовет исключение LinAlgError: Singular matrix .
Чтобы проверить, имеет ли матрица обратную, используйте метод det() из библиотеки NumPy, который возвращает определитель матрицы. Если определитель равен нулю, то матрица вырожденная и она не имеет обратной матрицы:
import numpy as np
matrix = np.array([[1, 2], [3, 4]])
determinant = np.linalg.det(matrix)
if determinant == 0:
print(«The matrix does not have an inverse.»)
else:
result = np.linalg.inv(matrix)
print(result)
Нахождение обратной матрицы с помощью циклов может быть достаточно сложным и трудоемким процессом, особенно для больших матриц. Поэтому рекомендуем использовать NumPy.
Заключение
Матрицы являются важной концепцией в линейной алгебре и часто используются в различных областях, таких как искусственный интеллект, графика и оптимизация. В Python представлено множество инструментов для работы с матрицами, включая библиотеку NumPy. Понимание матриц и их операций может быть полезным для решения множества практических задач в различных областях.
Источник: timeweb.cloud
Как читать программы в матрице? Подробный разбор.
В этом видео вы узнаете:
— Программы в Матрице. Как трактовать? Как связывать между собой?
— Программы в разных частях Матрицы.
— Как правильно читать программы? Стражник — Путь — Результат.
— Зоны в Матрице Судьбы.
— Понятие «Узел» в Матрице.
Станьте участником клуба «Исцеления Судьбы», присоединяйтесь к сообществу развивающихся духовно и личностно людей:
Понравилось? Расскажите друзьям:




Мы рекомендуем Вам также:


281 просмотров
Какие финансовые блоки необходимо проработать для выхода на доход?
В этом видео мы поговорим о финансовых блоках с позиции зеркальной матрицы и энергий.


154 просмотров
На что важно обратить внимание в матрице судьбы в первую очередь? Смогу ли я стать консультантом?
В этом видео: на что обратить внимание, хватаюсь за всё, но в итоге нигде, проблема с выбором и как медитировать?


220 просмотров
Нет цели и чувствую тупик. На что обратить внимание в зеркальной матрице судьбы?
На какую часть матрицы обратить внимание, когда потеря цели и нет понимания куда двигаться
Комментарии
Ответить с помощью Вконтакте:
of your page —>
Ответить с помощью Facebook:
Вам это понравится
- Клуб «Исцеление Судьбы»
- Энергопрогноз на каждый день
- Матрица Судьбы
- Нумерология
- Калькулятор Матрицы
Основное меню
Дополнительно
Контакты
Политика конфиденциальности
Политика конфиденциальности содержит пояснения о том, как используется информация, которую Вы мне предоставляете, и как связаться со мной, если у Вас возникнут вопросы и проблемы.
1. Какая информация нам необходима?
Если вы решаете подписаться на информационный продукт, размещенный на нашем сайте, мы запросим у Вас такую информацию, как имя и адрес электронной почты. Это объясняется следующими соображениями. Мы регулярно готовим актуальные информационные продукты (как платные, так и большое количество бесплатных) информационный маркетинг в интернет.
Ваш интерес к конкретному информационному продукту позволяет предположить, что и другие продукты информационный маркетинга в интернет и другие темы могут быть Вам интересны и полезны. Для того чтобы проинформировать Вас об этих продуктах, а также обеспечить к ним доступ, нам требуется отправить Вам информационное письмо. Кроме того, мы можем проводить опрос для выяснения Вашего мнения о наших продуктах, а также Ваших пожеланий. Перед тем как предоставить нам чужие персональные данные, обязательно получите разрешение соответствующих лиц. Убедитесь, что вы предоставляете правильные и точные сведения.
2. Что мы делаем с Вашей персональной информацией?
Адрес Вашей электронной почты и Ваше имя мы используем в следующих целях:
- для предоставления Вам информационных продуктов и услуг, а также проведения опросов с целью определения информации, в которой Вы нуждаетесь;
- для обработки Ваших запросов в службу поддержки;
- для рассылки новостей и рекламной информации о продуктах, услугах, специальных предложениях, продуктах и услугах избранных партнеров в пределах, разрешенных действующим законодательством, или в соответствии с Вашими пожеланиями (см. ниже раздел «Отказ от подписки»);
- для рассылки служебных сообщений (например, если Вы забыли свой пароль – применительно к продуктам, содержащим пароль);
- для предотвращения и выявления мошенничества и незаконного использования моих продуктов или услуг.
3. Кто еще получает доступ к персональной информации?
Для осуществления рассылки мы используем сервис почтовых рассылок. Этот сервис обрабатывает Вашу персональную информацию (т.е. e-mail и указанное Вами имя) для того, чтобы я мог отправить Вам электронное письмо с доступом к выбранному Вами продукту или проинформировать Вас о новых актуальных продуктах информационного маркетинга в интернет, или провести опрос с целью выявления информации, в которой Вы нуждаетесь. В исключительных обстоятельствах мы можем раскрыть Вашу персональную информацию, если этого требует закон или в целях защиты себя и других от противоправных действий или других опасностей.
4. Идентификационные файлы (cookies)
Наш сайт содержит идентификационные файлы, так называемые, cookies. Cookies – представляют собой небольшие текстовые файлы, отправляемые на компьютер посетителя сайта для учета его действий. Cookies используются на моем сайте для персонализации учета посещений, изучения поведения посетителей на сайте и регистрации их действий. Вы можете отключить использование cookies в параметрах настройки браузера. Следует учитывать, однако, что в этом случае некоторые функции будут недоступны или могут работать некорректно.
5. Безопасность
Как читать корреляционную матрицу
В статистике нас часто интересует понимание взаимосвязи между двумя переменными.
Например, мы можем захотеть понять взаимосвязь между количеством часов, отработанных студентом, и полученными им экзаменационными баллами.
Одним из способов количественной оценки этой взаимосвязи является использование коэффициента корреляции Пирсона , который является мерой линейной связи между двумя переменными . Он имеет значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Чем дальше коэффициент корреляции от нуля, тем сильнее связь между двумя переменными.
Но в некоторых случаях мы хотим понять корреляцию между более чем одной парой переменных. В этих случаях мы можем создать матрицу корреляции , представляющую собой квадратную таблицу, которая показывает коэффициенты корреляции между несколькими переменными.
Пример корреляционной матрицы
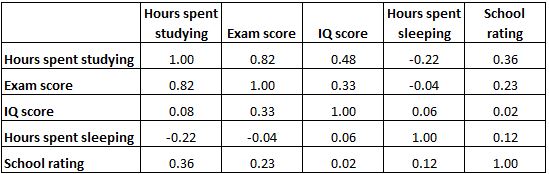
В приведенной ниже матрице корреляции показаны коэффициенты корреляции между несколькими переменными, связанными с образованием:
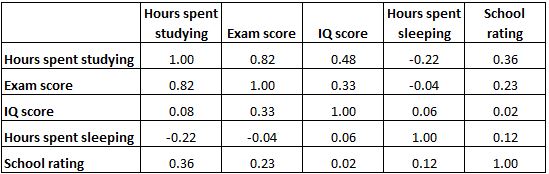
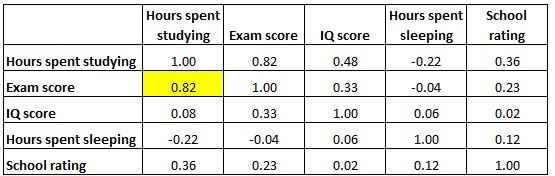
Каждая ячейка в таблице показывает корреляцию между двумя конкретными переменными. Например, выделенная ячейка ниже показывает, что корреляция между «часами, потраченными на учебу» и «оценкой за экзамен» составляет 0,82 , что указывает на сильную положительную корреляцию. Больше часов, потраченных на учебу, тесно связано с более высокими баллами на экзаменах.
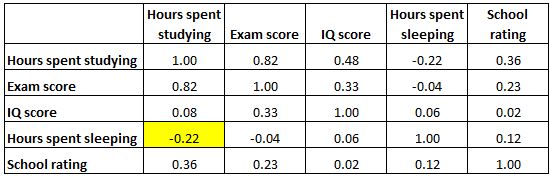
А выделенная ячейка ниже показывает, что корреляция между «часами, потраченными на учебу» и «часами, потраченными на сон» составляет -0,22 , что указывает на слабую отрицательную корреляцию. Больше часов, потраченных на учебу, связано с меньшим количеством часов, потраченных на сон.
А выделенная ячейка ниже показывает, что корреляция между «количеством часов, проведенных во сне» и «показателем IQ» составляет 0,06 , что указывает на то, что они в основном не связаны. Существует очень небольшая связь между количеством часов, которые студент спит, и его показателем IQ.
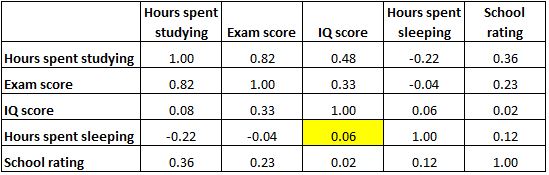
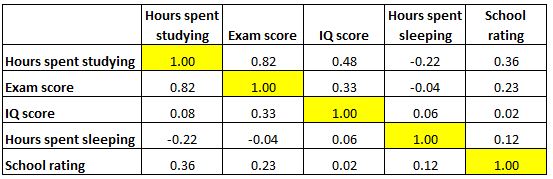
Также обратите внимание, что все коэффициенты корреляции по диагонали таблицы равны 1, потому что каждая переменная полностью коррелирует сама с собой. Эти ячейки бесполезны для интерпретации.
Вариации корреляционной матрицы
Обратите внимание, что корреляционная матрица совершенно симметрична. Например, верхняя правая ячейка показывает то же значение, что и нижняя левая ячейка:
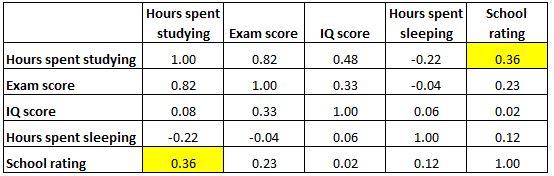
Это связано с тем, что обе ячейки измеряют корреляцию между «часами, потраченными на учебу» и «рейтингом школы».
Поскольку матрица корреляции симметрична, половина коэффициентов корреляции, показанных в матрице, являются избыточными и ненужными. Таким образом, иногда будет отображаться только половина корреляционной матрицы:
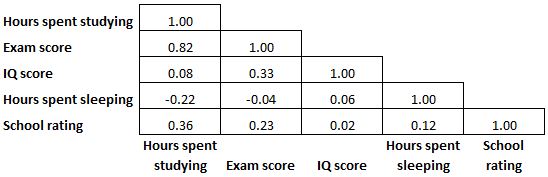
А иногда матрица корреляции раскрашивается, как тепловая карта, чтобы коэффициенты корреляции было еще легче читать:

Когда использовать корреляционную матрицу
На практике корреляционная матрица обычно используется по трем причинам:
1. Корреляционная матрица удобно обобщает набор данных.
Матрица корреляции — это простой способ суммировать корреляции между всеми переменными в наборе данных. Например, предположим, что у нас есть следующий набор данных, который содержит следующую информацию для 1000 учащихся:
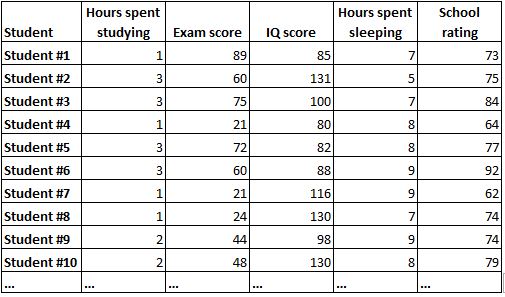
Было бы очень сложно понять взаимосвязь между каждой переменной, просто глядя на необработанные данные. К счастью, корреляционная матрица может помочь нам быстро понять корреляции между каждой парой переменных.
2. Корреляционная матрица служит диагностикой регрессии.
Одним из ключевых допущений множественной линейной регрессии является то, что ни одна независимая переменная в модели не имеет сильной корреляции с другой переменной в модели.
Когда две независимые переменные сильно коррелированы, это приводит к проблеме, известной как мультиколлинеарность , и может затруднить интерпретацию результатов регрессии.
Один из самых простых способов обнаружить потенциальную проблему мультиколлинеарности — посмотреть на матрицу корреляции и визуально проверить, сильно ли коррелируют какие-либо переменные друг с другом.
3. Корреляционная матрица может использоваться в качестве исходных данных для других анализов.
Корреляционная матрица используется в качестве исходных данных для других сложных анализов, таких как исследовательский факторный анализ и модели структурных уравнений.
Дополнительные ресурсы
В следующих руководствах объясняется, как создать корреляционную матрицу с помощью различных статистических программ:
Источник: www.codecamp.ru