Калькулятор Интегралов. Решение Определенных и Неопределенных Интегралов (первообразных)
Калькулятор интегрирует функции, используя методы: замены, рациональных функций и дробей, неопределенных коэффициентов, разложения на множители, дробно-линейных иррациональностей, Остроградского, прямые методы, интегрирование по частям, подстановки Эйлера, дифференциального бинома, интегрирования с модулем, интегральных функций, степенных, тригонометрических, гиперболических преобразований, понижения степени подынтегральной функции и группировок. Для решения определенных интегралов применяется формула Ньютона-Лейбница и нахождение пределов в точках разрыва
Введите выражение и нажмите или кнопку
Источник: mathdf.com
Интегралы для чайников: как решать, правила вычисления, объяснение

Интеграл: Азы интегрирования. Высшая математика
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять?
Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Изучаем понятие « интеграл »
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x).
Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов

Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции.
Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
- Производная от интеграла равна подынтегральной функции:

- Константу можно выносить из-под знака интеграла:

- Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

- Знак интеграла изменяется, если поменять местами пределы интегрирования:


Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Источник: zaochnik.ru
Интегрированное обучение — это что такое? Формы, технология и условия обучения

Интегрированное обучение — это что такое? Каждый ребенок имеет право на поддержку со стороны своих родителей и общества, чтобы расти, учиться и развиваться с ранних лет. А достигнув школьного возраста, дети должны ходить в школу и нормально восприниматься как учителями, так и сверстниками. Когда дети независимо от их различий получают образование вместе, все получают выгоду — это краеугольный камень инклюзивного образования.

Интегрированное обучение — это что такое?
Суть такого обучения заключается в том, что учащиеся разного уровня развития умственных и физических способностей учатся бок о бок в одном классе. Они с удовольствием посещают полевые и послешкольные мероприятия, вместе участвуют в ученическом самоуправлении, ходят на те же спортивные встречи, играют в игры.
Интегрированное обучение — это процесс, в котором ценится разнообразие и уникальный вклад каждого ученика в классе. В настоящей инклюзивной обстановке каждый ребенок чувствует себя в безопасности и имеет чувство принадлежности к группе. Учащиеся и их родители участвуют в определении образовательных целей и принятии решений, а у школьного персонала имеется достаточный уровень квалификации, поддержка, гибкость и ресурсы для воспитания, поощрения и удовлетворения потребностей всех учащихся.

Почему это так важно?
Интегрированное обучение обеспечивает более качественное образование детей и способствует изменению дискриминационных взглядов. Школа знакомит ребенка с миром вне их семей, помогает развивать социальные отношения и взаимодействия. Уважение и понимание возрастают, когда учащиеся с разными способностями и опытом играют, общаются и учатся вместе.
Интегрированное обучение детей не исключает и не разделяет членов коллектива, не способствует дискриминации по отношению к традиционно маргинализованным группам. Ведь индивидуальное специальное образование не гарантирует успех детям, которые нуждаются в особом внимании. Школы, которые обеспечивают поддержку и создают соответствующие условия интегрированного обучения, демонстрируют гораздо лучшие результаты.

Основные элементы интегрированного обучения
- Привлечение помощников, преподавателей или специалистов, которые будут помогать учителям в удовлетворении всех потребностей и нужд учащихся, работая со всей группой.
- Адаптированная учебная программа для детей с особыми образовательными потребностями.
- Участие родителей. Большинство школ стремятся к определенному уровню участия со стороны родителей, но часто это ограничивается лишь собраниями один раз в четверть.

Для всех и каждого
Интегрированное обучение — это принятие всех детей в обществе, независимо от их физического, интеллектуального, социального или языкового развития. Группа часто включает детей из неблагополучных групп населения, а также представителей всех рас и культур. В классе прекрасно сосуществуют одаренные ученики и ребята с ограниченными физическими возможностями.
Интеграция, конечно, не произойдет мгновенно, для нее требуется тщательное планирование, позитивное отношение, определенная модель поведения, использование необходимой специализированной поддержки, словом, нужно все для того, чтобы дети почувствовали себя частью школы, активно участвовали в системе образования, а затем стали полноправными членами общества.
Главная обязанность школьных учреждений заключается в том, чтобы охватить разнообразные и особые потребности всех учащихся, выявлять и минимизировать барьеры на пути обучения и общения, создавать толерантную и уважительную атмосферу, в которой каждый человек воспринимается как ценная личность. Таким образом, всем детям должна быть оказана поддержка, в которой они нуждаются, чтобы в будущем добиться успеха и найти себя в современном мире и обществе.
Преимущества интегрированного обучения
- Развитие индивидуальных способностей каждого ребенка.
- Вовлечение родителей в культурную, воспитательную и учебную деятельность школы.
- Формирование школьной культуры, уважения и сопричастности. Интегрированное обучение дает возможность узнать и принять индивидуальные различия, что позволит устранить риск появления преследований и издевательств в коллективе.
- Развитие дружеских отношений с широким кругом других детей, понимание их индивидуальных потребностей и способностей.

Новая система функционирования
Интегрированное обучение не является обязательным. В первую очередь стоит опираться на мнение родителей и желание самого ребенка. Грубо говоря, интеграция — это объединение отдельных составляющих в одно целое.
Что касается образования, то нельзя назвать этот процесс чисто механическим объединением здоровых детей и детей с какими-либо отклонениями. Это сложный набор взаимодействий между детьми, педагогами, специалистами по коррекции. Это не что-то локальное, ведь нужен целостный системный подход в организации деятельности школы по всем направлениям.

Инновационные технологии
Модернизация системы образования включает в себя активное использование инновационных идей и решений. Технология интегрированного обучения направлена на развитие познавательных и творческих способностей. На практике достигается целостное и глубокое понимание реальности окружающего мира. Обучение должно быть гармоничным сочетанием правил и творчества, науки и искусства. Инновационные технологии (объяснительно-иллюстрированного, личностно-ориентированного и развивающего обучения) здесь играют немаловажную роль.

Выделяют следующие формы интегрированного обучения:
- Комбинированная форма, при которой ребенок с особенностями психофизического развития способен учиться в классе наряду с абсолютно здоровыми детьми, получая необходимую регулярную поддержку и помощь специалистов (педагога-дефектолога, логопеда, психолога).
- Частичная интеграция, при которой ученики с отклонениями не способны наравне со сверстниками овладевать образовательной программой. Такие дети проводят в общих классах лишь часть времени, все остальное время — в спецклассах или на индивидуальных занятиях.
- Временная, при которой дети из особых классов и учащиеся обычных классов собираются не реже двух в месяц для совместных прогулок, проведения праздников, соревнований и других мероприятий воспитательного характера.
- Полная, при которой один-два ребенка с отклонениями в развитии обучаются в обычной группе. Такая форма больше подходит детям дошкольного и младшего школьного возраста. В основном, это дети, которые по уровню психофизического, речевого развития соответствуют возрастной норме и психологически готовы к совместному обучению со здоровыми сверстниками. Коррекционную помощь они получают по месту обучения, либо этим занимаются родители под контролем профессионалов.
Интегрированное обучение и воспитание является вполне привычной практикой в зарубежных странах. У нас же инклюзивные классы и школы лишь начинают появляться.
Источник: fb.ru
Решение интегралов. Рассказываем, как решать интегралы.
Интегралы и их решение многих пугает. Давайте избавимся от страхов и узнаем, что это такое и как решать интегралы! Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое.
Решение интегралов (интегрирование) есть операция обратная дифференцированию.
Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему.
В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .
Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b.
Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим:
Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3.
Попробуем решить тоже самое не прибегая к построению, используя интегрирование:
Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.
Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной.
F(x) – первообразная. Дифференцируя первообразную, мы получим исходное подынтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференцируем полученный ответ и сравниваем с исходным выражением.
Основные функции и первообразные для них приведены в таблице:
Таблица первообразных для решения интегралов
Основные приемы решения интегралов:
Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду.
Сначала следует запомнить основные свойства интегралов:
Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные приемы решения интегралов. Данные приемы охватывают большую часть заданий по теме нахождения интегралов.
Также мы рассмотрим несколько базовых примеров решения интегралов на базе этих приемов. Важно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.
Основные приемы решения интегралов
1. Замена переменной.
Для выполнения данного приема потребуется хороший навык нахождения производных.
2. Интегрирование по частям. Пользуются следующей формулой.
Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.
3. Интегрирование дробно-рациональных функций.
— разложить дробь на простейшие
— выделить полный квадрат.
— создать в числителе дифференциал знаменателя.
4. Интегрирование дробно-иррациональных функций.
— выделить под корнем полный квадрат
— создать в числителе дифференциал подкоренного выражения.
5. Интегрирование тригонометрических функций.
При интегрировании выражений вида
применяет формулы разложения для произведения.
Для выражений
m-нечетное, n –любое, создаем d(cosx). Используем тождество sin 2 +cos 2 =1
m,n – четные, sin 2 x=(1-cos2x)/2 и cos 2 x=(1+cos2x)/2
Для выражений вида:
— Применяем свойство tg 2 x=1/cos 2 x — 1
С базовыми приемами на этой всё. Теперь выведем своего рода алгоритм:
Алгоритм обучения решению интегралов:
1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования.
Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первообразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию.
2. Отработать использование таблицы первообразных и основным свойства интегралов. Необходимо научиться пользоваться таблицей первообразных. По множеству функций первообразные найдены и занесены в таблицу. Если мы имеем интеграл, которые есть в таблице, можно сказать, что он решен.
3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференцируем полученное выражение и сравниваем с исходным интегралом.
Отработаем основные моменты на нескольких примерах:
Примеры решения интегралов
Пример 1:
Решить интеграл: 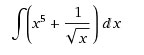
Интеграл неопределенный. Находим первообразную.
Для этого интеграл суммы разложим на сумму интегралов. 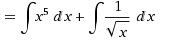
Каждый из интегралов табличного вида. Смотрим первообразные по таблице.
Решение интеграла: 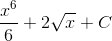
Проверим решение(найдем производную): 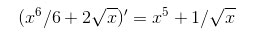
Пример 2. Решаем интеграл
Интеграл неопределенный. Находим первообразную.
Сравниваем с таблицей. В таблице нет.
Разложить, пользуясь свойствами, нельзя.
Смотрим приемы. Наиболее подходит замена переменной.
Заменяем х+5 на t 5 . t 5 = x+5 . Получаем.
Но dx нужно тоже заменить на t. x= t 5 — 5, dx = (t 5 — 5)’ = 5t 4 . Подставляем:
Интеграл из таблицы. Считаем:
Подставляем в ответ вместо t ,
Пример 3. Решение интеграла: 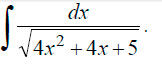
Для решения в этом случае необходимо выделить полный квадрат. Выделяем: 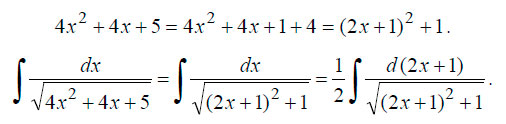
В данном случае коэффициент 1/2 перед интегралом получился в результате замены dx на 1/2*d(2x+1). Если вы найдете производные x’ = 1 и 1/2*(2x+1)’= 1, то поймете почему так.
В результате мы привели интеграл к табличному виду.
Находим первообразную. 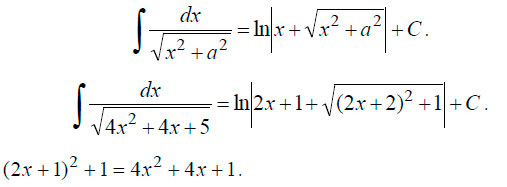
В итоге получаем:
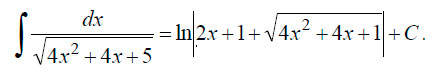
Для закрепления темы интегралов рекомендуем также посмотреть видео.
В нем мы на примере физики показываем практическое применение интегрирования, а также решаем еще несколько задач.
Надеюсь вопрос, как решать интегралы для вас прояснился. Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов, пишите в комментариях.
Рекламная заметка: Для особо пытливых умов советуем Видео-лекции по математическому программированию . Программирование одна из дочек математики!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Источник: reshit.ru
Интегрирование функции, заданной таблично
Если подынтегральная функция задана таблично в виде пар значений x(i),y(i) (узлов), то интеграл можно вычислить несколькими способами. Первый заключается в том, чтобы выразить зависимость y от x какой-либо подходящей, т. е. решить задачу аппроксимации или интерполяции табличных данных. Затем эта зависимость используется для интегрирования функции методами, описанными выше. Выбор аппроксимирующей и интерполирующей функции, а также методы расчета их параметров описаны в соответствующем разделе.
Задачу интегрирования таблично заданной функции можно решить, не прибегая к построению аппроксимирующей (интерполирующей) функции. Если табличные данные приводятся с постоянным и достаточно маленьким шагом по х, то можно применить квадратурные формулы. Пределы интегрирования могут быть любыми в пределах табличных данных и совпадать с узлами.
В программе 20 выполнен расчет с помощью метода Симпсона (он оптимален для интегрирования табличных зависимостей). Единственным его недостатком является требование четности интервалов интегрирования N. А изменить количество интервалов интегрирования таблично заданной функции мы не можем.
Для метода трапеций этой проблемы нет и в программе 20 приведен также расчет методом трапеций. Для иллюстрации точности интегрирования в программе 20 в качестве табличных данных взята синусоидальная зависимость с точностью до третьего знака после запятой. С такой же точностью поручены, как видно из листинга программы, и значения интегралов. Это правило выполняется всегда: чем точнее задана таблица, тем точнее можно вычислить интеграл и тем менее точный метод интегрирования можно использовать.
Если же шаг интегрирования не постоянный. А это часто бывает с экспериментальными табличными данными, то лучше воспользоваться первым способом: построить аппроксимирующую (интерполирующую) функцию. В программе 21 приведены три наиболее компактные формы интерполяции и аппроксимации табличных данных для целей интегрирования. Как видно из листинга программы, наибольшую точность дают кубическая сплайн-интерполяция и аппроксимация полиномом (в данном случае четвертой степени).
Программа 20
Программа 21
Расчет изменений термодинамических функций в ходе химической реакции по интегральным уравнениям
В основе расчета изменений термодинамических функций: энтальпии rH 0 Т, энтропии rS 0 Т и энергии Гиббса rG 0 Т , а также константы равновесия для химической реакции лежат соответствующие дифференциальные уравнения и их интегральные формы, представленные в таблице 7 [11].
Источник: studfile.net