Программа и схема вычисления что это

Линейный алгоритм. Понятие и особенности. Блок-схема

Каждый человек на протяжении своей жизни решает множество задач разной сложности. Но даже самые простые из задач выполняются последовательно, то есть за несколько шагов. Эту последовательность можно назвать алгоритмом. Последовательности бывают разные, но начинать их изучение лучше всего с линейных.

Прежде чем приступить к рассмотрению основной темы статьи, следует сделать краткое отступление и сказать несколько слов про алгоритмический язык.

Алгоритмический язык

Представьте, что человеку, работающему за компьютером, поставлена некая вычислительная задача. В языке программирования решение этой задачи выполняется с помощью алгоритмизации. Решение предполагает: — разбиение на этапы; — разработку алгоритма; — составление программы решения на алгоритмическом языке; — ввод данных; — отладку программы (возможны ошибки — их надо исправить); — выполнение на ПК; — анализ результатов.

Алгоритмический язык является средством описания алгоритмов, а уже алгоритм, в свою очередь, представляет собой чёткое описание определённой последовательности действий, направленных на решение необходимой задачи.

Алгоритм инверсного вычисления программ

Свойства алгоритма

Их несколько: — конечность. Любой алгоритм должен быть завершённым, а окончание наступает после выполнения определённого числа шагов; — однозначность, понятность. Не допускается разных толкований, неопределённости и двусмысленности — всё должно быть чётко и ясно, а также понятно исполнителю — и правила выполнения действий линейного алгоритма, и сами действия; — результативность. Итог работы — результат, полученный за конечное число шагов; — универсальность, массовость. Качественный алгоритм способен решать не одну задачу, а целый класс задач, имеющих схожую постановку/структуру.

Линейная структура

Любой алгоритм составляется из ряда базовых структур. Простейшей базовой структурой является следование — структура с линейными характеристиками. Из этого можно сформулировать определение.

Линейный алгоритм — это алгоритм, образуемый командами, которые выполняются однократно и именно в той последовательности, в которой записаны. Линейная структура, по сути, проста. Записать её можно как в текстовой, так и в графической форме.

Представим, что у нас стоит задача пропылесосить ковёр в комнате. В текстовой форме алгоритм будет следующим: — принести пылесос к месту уборки; — включить; — пропылесосить; — выключить; — унести пылесос.

И каждый раз, когда нам надо будет пылесосить, мы будем выполнять один и тот же алгоритм.

Теперь поговорим про графическую форму представления.

Блок-схема

Для изображения алгоритма графически используют блок-схемы. Они представляют собой геометрические фигуры (блоки), соединённые стрелками. Стрелки показывают связь между этапами и последовательность их выполнения. Каждый блок сопровождается надписью.

Рассмотрим фигуры, которые используются при визуализации типичной линейной последовательности.

Блок-схема программы для вычисления факториала

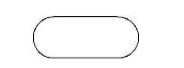
Блок ввода-вывода данных (отображает список вводимых и выводимых переменных):

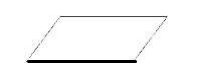
Арифметический блок (отображает арифметическую операцию/группу операций):

Условный блок (позволяет описать условие). Алгоритмы с таким блоком используются при графической визуализации алгоритмов с ветвлением:

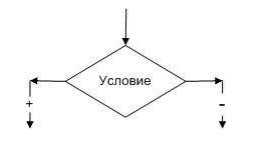
Условного блока нет в классическом линейном алгоритме, так как в нём, как уже было сказано ранее, все операции выполняются последовательно, то есть одна за другой. В линейном алгоритме размещение блоков выглядит следующим образом:

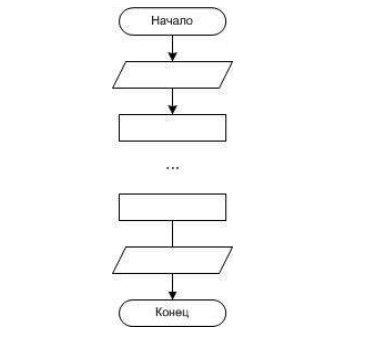
А вот, как решается задача по нахождению площади треугольника по формуле Герона. Здесь a, b, c – это длины сторон, S – площадь треугольника, P – периметр.

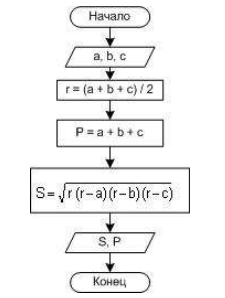
Следует обратить внимание, что запись «=» — это не математическое равенство, а операция присваивания. В результате этой операции переменная, стоящая слева от оператора, получает значение, которое указано справа. Значение не обязательно должно быть сразу определено (a = 3) — оно может вычисляться посредством выражения (a = b + z), где b = 1, a z = 2.

Примеры линейных алгоритмов

Если рассмотреть примеры решения на языке Pascal (именно этот язык до сих пор используется для изучения основ алгоритмизации и программирования), то можно увидеть следующую картину:

И, соответственно, блок-схема программы линейной структуры будет выглядеть следующим образом:

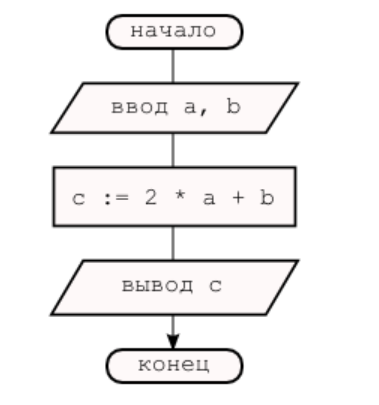
Как составить программу линейной структуры?

Порядок следующий: — определите, что именно относится к исходным данными, а также каков типы/класс этих данных, выберите имена переменных; — определите, каков тип данных будет у искомого результата, выберите название переменных (переменной); — определите, какие математические формулы связывают результат и исходные данные; — если требуется наличие промежуточных данных, определите класс/типы этих данных и выберите имена; — опишите все используемые переменные; — запишите окончательный алгоритм. Он должен включать в себя ввод данных, вычисления, вывод результатов.

На этом всё, в следующий раз рассмотрим на примерах программу разветвлённой структуры. Если же вас интересует тема алгоритмизации в контексте разработки программного обеспечения, ждём вас на профессиональном курсе OTUS!

Источник: otus.ru

Урок 4. Блок-схема

Итак, опустив долгие и нудные восхваления Паскаля, которые так любят публиковать в своих статьях редакторы многих сайтов, приступим непосредственно к самому основному – к программированию.

В школах, как правило, изучение Паскаля начинают с решения простейших задач путем составления различных алгоритмов или блок-схем, которое многие так часто игнорируют, считая никому не нужной ерундой. А зря. Я, как и любой другой человек, хоть немного соображающий в программировании (не важно где – в Паскале, Си, Дельфи), могу уверить Вас – умение правильно и быстро составлять схемы является фундаментом, основой программирования.

Блок-схема — графическое представление алгоритма. Она состоит из функциональных блоков, которые выполняют различные назначения (ввод/вывод, начало/конец, вызов функции и т.д.).

Существует несколько основных видов блоков, которые нетрудно запомнить:

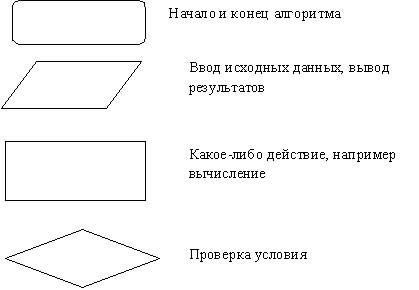
Сегодняшний урок я решила посвятить не только изучению блок-схем, но также и изучению линейных алгоритмов. Как Вы помните, линейный алгоритм — наипростейший вид алгоритма. Его главная особенность в том, что он не содержит никаких особенностей. Как раз это и делает работу с ним простой и приятной.

Задача №1: «Рассчитать площадь и периметр прямоугольника по двум известным сторонам».

Данная задача не должна представлять особой трудности, так как построена она на хорошо известных всем нам формулах расчета площади и периметра прямоугольника, поэтому зацикливаться на выведении этих формул мы не будем.

Составим алгоритм решения подобных задач:

1) Прочитать задачу.
2) Выписать известные и неизвестные нам переменные в «дано». (В задаче №1 к известным переменным относятся стороны: a, b ;к неизвестным — площадь S и периметр P)
3) Вспомнить либо составить необходимые формулы. (У нас: S=a*b; P=2*(a+b))
4) Составить блок-схему.
5) Записать решение на языке программирования Pascal.

Запишем условие в более кратком виде.

Структура программы, решающей данную задачу, тоже проста:

• 1) Описание переменных;
• 2) Ввод значений сторон прямоугольника;
• 3) Расчет площади прямоугольника;
• 4) Расчет периметра прямоугольника;
• 5) Вывод значений площади и периметра;
• 6) Конец.

А вот и решение:

Program Rectangle; Var a, b, S, P: integer; Begin write(‘Введите стороны прямоугольника!’); readln(a, b); S:=a*b; P:=2*(a+b); writeln(‘Площадь прямоугольника: ‘, S); write(‘Периметр прямоугольника: ‘, P); End.

Задача №2: Скорость первого автомобиля — V1 км/ч, второго – V2 км/ч, расстояние между ними S км. Какое расстояние будет между ними через T часов, если автомобили движутся в разные стороны? Значения V1, V2, T и S задаются с клавиатуры.

Решение осуществляем, опять же, следуя алгоритму. Прочитав текст, мы переходим к следующему пункту. Как и во всех физических или математических задачах, это запись условий задачи:

Дано: V1, V2, S, Т
Найти: S1

Далее идет самая главная и в то же время самая интересная часть нашего решения – составление нужных нам формул. Как правило, на начальных стадиях обучения все необходимые формулы хорошо нам известны и взяты из других технических дисциплин (например, на нахождение площади различных фигур, на нахождение скорости, расстояния и т.п.).

Формула, используемая для решения нашей задачи, выглядит следующим образом:

Следующий пункт алгоритма – блок-схема:

А также решение, записанное в Pascal :

Program Rasstoyanie; Var V1, V2, S, T, S1: integer; begin write(‘Введите скорость первого автомобиля: ‘); readln(V1); write(‘Введите скорость второго автомобиля: ‘); readln(V2); write(‘Введите время: ‘); readln(T); write(‘Введите расстояние между автомобилями: ‘); readln(S); S1:=(V1+V2)*T+S; writeln(‘Через ‘, t,’ч. расстояние ‘, S1,’ км.’); End.

Вам может показаться, что две эти программы правильны, но это не так. Ведь сторона треугольника может быть 4.5, а не 4, а скорость машины не обязательно круглое число! А Integer — это только целые числа. Поэтому при попытке написать во второй программе другие числа выскакивает ошибка:

Чтобы решить эту проблему вам надо вспомнить какой тип в Pascal отвечает за нецелые числа. В этом уроке мы рассматривали основные типы. Итак, это вещественный тип — Real. Вот, как выглядит исправленная программа:

Как видите, эта статья полезна для прочтения как новичкам, так и уже более опытными пользователям Pascal, так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие.

(10 оценок, среднее: 4,10 из 5)
KOKS1999 :
Здесь понятней чем в школе.

мля… прикиньте, я узнал про этот сайт только ПОСЛЕ того как сделал программу с условием, узнавая все в инструкции

Ребята , вопрос на засыпку, как заставить «,» (введенную пользователем в числе) заменить на «.» внутри программы, что бы не вылетало юхни с ошибкой.

AciDWarrioR :

Взять строку введенную пользователем, заменить «,» на «.».
Если совсем гуглить не умеете, то вам сюда — http://www.cyberforum.ru/pascal/thread190664.html

rrrFer rrrFer :

>> скорость машины не обязательно круглое число! Нет такого понятия, как «круглое число». Обе ваши блок-схемы не соответствуют ГОСТу (сдать такие на курсовой проект не получится). ГОСТ определяет блоки начала и конца, как «прямоугольник со скругленными краями», а не «скругленными углами». >> умение правильно и быстро составлять схемы является фундаментом, основой программирования.

Большинство программистов так не считает. Кроме того, попробуйте поспрашивать у программистов «когда они последний раз составляли блок-схему?» — окажется что в ВУЗе (когда с них зачем-то сдирали знание ГОСТа). >> так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие. Очень сложное, долгое и бесполезное занятие. Для хоть сколько-нибудь большой программы (в тысячу строк хотя бы, как курсак) блок-схемы будут огромные и их будут десятки. А что делать если они перестают соответствовать коду? — вот даже в вашей первой задаче надо будет добавить проверку, что юзер не ввел отрицательные значения сторон, что делать? — исправления кода займут 1 минуту, а исправление блок-схем 10 минут, и зачем тогда этим заниматься?

Аноним :

Программист не должен писать блок-схемы (он их должен читать и понимать и при необходимости исправлять). Блок-схемы это графический язык общения, который понимает как программист, так и не программист. Чтобы пользователь не общался с программистом своими «хотелками», типа я хочу, чтобы вот это правильно считалось, и это число складывалось с этим, а потом выводилось сюда (или вообще говорил — хочу что бы работало), а рисовал все в виде блок-схем с четким алгоритмом. Тогда по идее у программиста будет понимание того, что от него хотят (и он через пять минут не забудет все что ему сказали). Либо, когда общаются два программиста пишущих на разных языках программирования (LISP и Java) и одному нужно объяснить как работает его код, что бы другой переписал его на другом языке.
Как объяснить преподавателю как работает программа, если преподаватель не знает языка программирования на котором написана ваша программа? Или как преподавателю объяснить алгоритм задачи студентам пишущим и реализующим этот алгоритм или программу на разных языках программирования? Нужен какой-то универсальный язык общения и обычно это просто текст «что нужно сделать» на русском языке, а не намного облегчающая жизнь программиста блок-схема.
Вам могут сказать — сделай модуль авторизации (ты же знаешь как, ну как всегда и как везде), а могут нарисовать блок-схему модуля авторизации с учетом всех пожеланий, типа того, что пароль должен содержать не менее 6 символов и что нужно делать в противном случае т.д. То есть блок схему должен уметь рисовать тот кто ставит задачу, а не программист. Либо программист (архитектор либо менеджер проекта), который ставит задачу другим программистам.

Вы слишком придирчивы, серьезно (я говорю про последние два пункта). Понятно, что статья (как почти и весь сайт) написана почти только для школьников, которым об этом твердят в школе. Здесь же им просто объясняют те вещи, которые они на учебе недопоняли

Блок схемы всей программы могут не понадобиться. Это же тонны бумаги и много времени. И да, они устаревают и актуализировать их трудоёмко.
Но при обсуждении новых вариантов решения задачи с другими программистами удобно оперировать блоками с криво-косо нарисованными краями и линиями. Начертил на бумаге или доске и все понятно.
На практике я встречал фотографии доски с блок-схемами, прикреплённые к задачам в Jira.
Не по ГОСТу

Программист :
Спасибо, теперь я напишу программу, которая делает код по блок схеме и наоборот

program Logarifm;
Var
X,y,z:real;
function Lgrfm(A,B:Real):Real;
var
Osn:Real;
begin
Osn:=ln(A)/ln(B);
Lgrfm:=Osn;
end;
begin
Write(‘Введите X = ‘);
ReadLn(X);
Write(‘Введите Y = ‘);
ReadLn(Y);
Z:=Lgrfm(X,2)+Lgrfm(Y,3);
WriteLn(‘Z = ‘,Z:10:3);
ReadLn;
end.

Отличный сайт, мне все нравится все понятно и четко, нашел нужные программы.
фцуыва :
паогшел нах@й
Василий :

В блок-схемах начало и конец алгоритма обозначаются не прямоугольником со скруглёнными краями, а овалом!

Дмитрий И :

Ребята, что сделали сайт молодцы)) Оч полезная инфа, что нужно поправить, чтобы сайт стал еще лучше:
1) мне не хватает структуры уроков порядковой (или хотябы под уроками чтобы была ссылка на следующий), поэтому приходится на другие уроки искать ссылки по сайту и в контексте уроков;
2)нет описания функций используемых в примерах (по крайней мере, возможно по причине отсутствия структуры, я их не нашел), поэтому беру на сторонних ресурсах описания таких функций как dec() inc() sqr() odd().
А вообще как я понял сайт составлялся школьниками «на коленках», поэтому я не придираюсь, а просто говорю им спасибо за их труд. Желаю успехов.

Источник: learnpascal.ru

Программа и схема вычисления что это

В рамках этого задания мы займёмся развитием алгоритмического мышления, и будем рассматривать различные положения теории алгоритмов. Прежде всего, определим понятие «Алгоритм».

ОПРЕДЕЛЕНИЕ

Алгоритм – это последовательность действий, преобразующая исходные данные в результат и обладающая некоторыми свойствами.

Приведённое определение не является строгим, поскольку в нём присутствует ссылка на «некоторые свойства». Чтобы подробно описать понятие Алгоритма рассмотрим эти свойства.

1) Конечность. Последовательность действий является алгоритмом только тогда, когда преобразование любых допустимых входных данных в результат происходит за конечное число шагов.

Например, можно составить алгоритм для решения задачи: «Выпишите в строчку все цифры двадцатеричной системы счисления», но нельзя составить алгоритм для решения задачи: «Выпишите все натуральные числа», поскольку в этом случае количество действий – бесконечное.

2) Детерминированность. Это свойство обозначает, что если применить алгоритм сколь угодно раз к одним и тем же входным данным, результат всегда получится одинаковым.

3) Дискретность. О данном понятии рассказывалось в рамках предыдущего задания по алгебре логики. Свойство дискретности применительно к алгоритму обозначает, что выполнение алгоритма разбивается на последовательность законченных действий. То есть каждое действие должно завершиться, прежде чем начнётся следующее.

4) Понятность. Чтобы описать это свойство, стоит упомянуть, что алгоритм всегда рассчитан на некоторого конкретного исполнителя, который умеет производить некоторый набор действий. Свойство понятности заключается в том, что все действия, входящие в алгоритм должны принадлежать к набору действий исполнителя.

Набор действий, которые может исполнить исполнитель, называется «системой команд». Стоит отметить, что исполнитель не должен ничего додумывать. Его задача – исключительно исполнять команды.

5) Массовость. Это свойство означает, что алгоритм пишется не для одних конкретных входных данных, а для некоторого множества задач. В отличие от предыдущих свойств, которые являются просто неотъемлемой частью любого алгоритма, свойство массовости является ещё и характеристикой алгоритма, то есть можно говорить, что алгоритм `»A»` является более массовым, чем алгоритм `»C»`. Это будет означать, что все задачи, которые можно решить алгоритмом C также можно решить и алгоритмом `»A»`, но существуют задачи, которые можно решить алгоритмом `»A»` и нельзя решить алгоритмом `»C»`.

Рассмотрим несколько примеров исполнителей алгоритмов.

ПРИМЕРЫ ИСПОЛНИТЕЛЕЙ АЛГОРИТМОВ

1) Исполнителем является любой человек сознательного возраста. Здесь могут решаться такие задачи как переход улицы, приём пищи, приготовление сладкого стола, украшение комнаты и т. д. Для всех перечисленных задач можно составить алгоритмы. Например, классический алгоритм перехода улицы формулируется так: «Посмотри налево, если ближе некоторого расстояния нет машин, иди до середины дороги, остановись, посмотри направо, и если ближе некоторого расстояния нет машин, то иди до конца». В приведённой формулировке есть переменная величина – безопасное расстояние, на котором могут находиться машины. Она зависит от конкретного человека, поэтому для конкретного человека наш алгоритм надо будет уточнять.

2) Исполнителем является человек, обладающий определёнными умениями. Один из простых примеров задач для такого исполнителя – это удаление аппендицита. Алгоритм составить можно, но исполнять его может не любой человек, а только тот, кто обладает умением хирургического вмешательства.

3) Исполнителем может быть робот, живущий в прямоугольном лабиринте и умеющий ходить в разные стороны. В этом случае можно поставить задачу перехода из одной точки лабиринта в другую и составить алгоритм её решения.

4) Исполнителем может являться компьютер. Здесь, как и для человека, можно поставить огромный набор задач. Примеры рассмотрим в дальнейшем.

Как уже упоминалось выше, у каждого исполнителя есть своя система команд – набор простых действий, которые может выполнить данный исполнитель. Если мы составляем алгоритм для этого исполнителя, то все шаги алгоритма должны входить в систему команд исполнителя. Наиболее простым из рассмотренных исполнителей является робот в лабиринте. Его система команд достаточно простая, и мы можем легко выписать её:

«ИДИ ВПРАВО НА 1 КЛЕТКУ»

«ИДИ ВЛЕВО НА 1 КЛЕТКУ»

«ИДИ ВВЕРХ НА 1 КЛЕТКУ»

«ИДИ ВНИЗ НА 1 КЛЕТКУ»

«ПРОВЕРЬ НАЛИЧИЕ СТЕНКИ СПРАВА»

«ПРОВЕРЬ НАЛИЧИЕ СТЕНКИ СЛЕВА»

«ПРОВЕРЬ НАЛИЧИЕ СТЕНКИ СВЕРХУ»

«ПРОВЕРЬ НАЛИЧИЕ СТЕНКИ СНИЗУ»

Очевидно, что уже у такого простого исполнителя набор команд неоднородный. Есть команды, результатом которых является сдвиг робота, а есть команды проверки, результатом которых является логическое значение «Истина» или «Ложь». (Подробно о логических значениях рассказывалось в рамках прошлого задания). Наличие команд проверки позволит нам ввести алгоритмические конструкции ветвления и цикла, но об этом чуть позже.

При изучении алгоритмов для лучшего понимания иногда мы будем пользоваться псевдоисполнителем алгоритмов, языком которого является блок-схема. Блок-схема является достаточно удобным представлением алгоритма, чтобы проследить логику его выполнения. Состоит она из блоков и связей между блоками. Связи обозначаются стрелками, которые показывают последовательность исполнения блоков. Из блоков нас будут интересовать 4 типа:

1) Начало/Конец алгоритма

2) Получение исходных данных/Выдача результатов

3) Линейное вычисление

4) Ветвление

В блок-схемы линейный участок обозначается прямоугольником. Все команды, записанные в прямоугольнике, исполняются ровно в том порядке, в котором они записаны (будем считать, что сверху вниз). Аналогично Паскалю, будем отделять команды друг от друга в линейном блоке точкой с запятой. Присваивание также будем обозначать символом «`:=`», а вот арифметическое выражение можно записывать, используя как синтаксис Паскаля, так и математики (этим можно пользоваться при решении задач). Аналогично с арифметическим, логическое выражение можно записывать, используя как синтаксис Паскаля, так и алгебры логики.

Алгоритм на языке блок-схемы всегда начинается с блока начала, затем идёт блок ввода входных данных, если они есть, далее блок вычислений, затем блок вывода результата и блок завершения алгоритма. В качестве примера рассмотрим блок-схему вычисления площади треугольника по длинам его `3` сторон с использованием формулы Герона. Входными данными в этой задаче являются длины сторон, а результатом – значение площади. Соответственно, мы будем решать задачу, используя пять переменных. Три стороны – a, b, c . Площадь – s . И полупериметр – p . Будем считать, что стороны всегда будут заданы таким образом, что треугольник существует. Рассмотрим блок-схему решения этой задачи:

В блок-схемы линейный участок обозначается прямоугольником. Все команды, записанные в прямоугольнике, исполняются ровно в том порядке, в котором они записаны (будем считать, что сверху вниз). Аналогично Паскалю, будем отделять команды друг от друга в линейном блоке точкой с запятой. Присваивание также будем обозначать символом «`:=`», а вот арифметическое выражение можно записывать, используя как синтаксис Паскаля, так и математики (этим можно пользоваться при решении задач). Аналогично с арифметическим, логическое выражение можно записывать, используя как синтаксис Паскаля, так и алгебры логики.

Алгоритм на языке блок-схемы всегда начинается с блока начала, затем идёт блок ввода входных данных, если они есть, далее блок вычислений, затем блок вывода результата и блок завершения алгоритма. В качестве примера рассмотрим блок-схему вычисления площади треугольника по длинам его `3` сторон с использованием формулы Герона. Входными данными в этой задаче являются длины сторон, а результатом – значение площади. Соответственно, мы будем решать задачу, используя пять переменных. Три стороны – a, b, c . Площадь – s . И полупериметр – p . Будем считать, что стороны всегда будут заданы таким образом, что треугольник существует. Рассмотрим блок-схему решения этой задачи:

Источник: zftsh.online

Вычисление значения многочлена. Все ли тривиально в этом вопросе?

Вычисление значения многочлена в точке является одной из простейших классических задач программирования.
При проведении различного рода вычислений часто приходится определять значения многочленов при заданных значениях аргументов. Часто приближенное вычисление функций сводится к вычислению аппроксимирующих многочленов.
Рядового читателя Хабрахабр нельзя назвать неискушенным в применении всяческих извращений. Каждый второй скажет, что многочлен надо вычислять по правилу Горнера. Но всегда есть маленькое «но», всегда ли схема Горнера является самой эффективной?

Я не ставлю цель точно описать алгоритмы для вычисления многочленов, а лишь показать, что в некоторых случаях можно (нужно) применять схемы отличные правила Горнера. Для тех, кого заинтересует материал, в конце статьи приведен список литературы, с которой можно ознакомиться для более детального изучения вопроса.
Кроме того, иногда становиться обидно, что фамилии наших русских математиков остаются малоизвестными. К тому же мне просто приятно рассказать о работах наших математиков.

Схема Горнера

При вычислении значений многочленов очень широкое применение получило правило Горнера. Метод назван в честь британского математика Уильяма Джорджа Горнера.
В соответствии с этим правилом многочлен n-й степени:

представляется в виде

Вычисление значения многочлена производится в порядке, определяемом скобками. Что имеем? Чтобы вычислить многочлен по схеме Горнера, надо выполнить n умножений и n-k сложений (здесь k – число коэффициентов многочлена, равных 0). Если , то умножений будет n-1.
Можно показать, что для вычисления многочленов, общего вида нельзя построить схему более экономичную по числу операций, чем схема Горнера.
Самая большая привлекательность схемы Горнера состоит в простоте алгоритма для вычисления значения многочлена.

Исключения

При вычислении многочленов специального вида может потребоваться меньшее число операций, чем при применении универсальной схемы Горнера. Например, вычисление степени по схеме Горнера означает последовательное перемножение n множителей и требует n-1 умножение. Однако каждый первый читатель скажет, что для вычисления, например, нужно последовательно вычислить , , , т.е. выполнить всего 3 умножения вместо 7.

А есть что-то еще, ведь схема Горнера самая экономичная?

На самом деле все решают объемы вычислений. Если надо вычислить одно значение многочлена, то лучше схемы Горнера ничего не придумано. Но если значения многочлена вычисляются во многих точках, то появляется возможность сэкономить большое число операций умножения за счет предварительных вычислений, выполняемых ровно один раз. Это может значительно ускорить работу программы.

В некоторых случаях для получения значений полиномов целесообразно использовать двухэтапные схемы. На первом этапе выполняются действия только над коэффициентами многочлена, он преобразуется к специальному виду. На втором же этапе вычисляют уже значение самого многочлена при заданных значениях аргумента. При этом может оказаться, что количество операций, выполняемых на втором этапе будет меньше, чем при вычислениях по схеме Горнера.

Снова замечу, что такие методы вычислений целесообразны при вычислении значений многочлена для большого числа значений x. Выигрыш получается, за счет того, что первый этап для многочлена выполняется лишь один раз. Примером может послужить вычисление элементарных функций, где приближающий многочлен готовиться заранее.

В дальнейших рассуждениях, говоря о количестве операций для вычисления , я буду иметь в виду сложность второго этапа вычислений.

Схема Дж.Тодта для многочленов 6 степени

Имеем следующий многочлен:

Для вычислений используем следующие вспомогательные многочлены:

Коэффициенты определяются методом неопределенных коэффициентов исходя из условия . Из последнего условия составляем систему уравнений, приравнивая коэффициенты при равных степенях многочленов.

Саму систему, здесь приводить не буду. Но она легко решается методом подстановок, при этом приходится решать квадратные уравнения. Коэффициенты могут получиться комплексными, но если коэффициенты оказываются действительными, то вычисления требуют трех умножений и семи сложений вместо пяти умножений и шести сложений по схеме Горнера.

Говорить об универсальности данной схемы не приходится, но зато читатель наглядно может оценить уменьшение числа операций по сравнению со схемой Горнера.

Схема Ю.Л. Кеткова

Наконец-то, добрался и до наших математиков.

Ю.Л. Кетков дал общее представление многочлена n-й степени для n>5, всегда приводящее к действительным выражениям и требующее для вычисления многочлене n-й степени выполнения [(n+1)/2]+[n/4] умножений и n+1 сложений.

Например, при n=2k схема Кеткова сводится к нахождению многочленов:

где , при k –четном, и , , если k нечетное (k>2).

Все неизвестные коэффициенты находятся из равенства . В работах Кеткова для решения получающихся систем дается метод, дающий всегда действительные коэффициенты .

Схемы В.Я. Пана

Э. Белага в своих работах дал строгое доказательство невозможности построения схемы вычисления произвольных многочленов n-й степени, использующей на втором этапе меньше, чем [(n+1)/2]+1 умножений и n сложений.

В.Я. Пан занимался вопросами оптимального вычисления многочленов. В частности, им предложено несколько схем для вычисления действительных многочленов, которые весьма близко подобрались к оценкам Э. Белаги. Приведу некоторые схемы Пана для действительных многочленов.
1. Схема для вычисления многочленов четвертой степени.
Рассматривается многочлен .

Представим в виде:

2. Схема для вычисления , .
Строим вспомогательные многочлены , , :

Для вычисления значения многочлена используем выражения:

Эта схема на втором этапе требует умножения и сложения.

Особенностью данной схемы является то, что коэффициенты всегда существуют при и действительных коэффициентах исходного многочлена.

У В.Я. Пана существуют и другие схемы для вычисления многочленов, в том числе и для комплексных.

Заключение

Резюмируя сказанное, замечу, что вычисление одного или нескольких значений полинома бесспорно нужно проводить с использованием схемы Горнера.

Однако, если число значений полинома, которые потребуется вычислить велико, а производительность очень важна, то имеет смысл рассмотреть применение специальных методов вычисления многочленов.

Некоторые читатели скажут, что возиться с применением схем, отличных от схемы Горнера, сложно, муторно и не стоит с этим связываться. Однако в реальной жизни встречаются задачи, в которых требуется вычислять просто огромное число значений многочленов с большими степенями (например, на их вычисление могут уходить месяцы), и уменьшение числа умножений в два раза даст существенный выигрыш во времени, даже если вам придется потратить пару дней на реализацию конкретной схемы для вычисления многочленов.

Литература

1. Кетков Ю.Л. Об одном способе вычисления полиномов на математических машинах. // Известия ВУЗ’ов. Радиофизика, т.1., № 4, 1958
2. В. Я. Пан, “Вычисление многочленов по схемам с предварительной обработкой коэффициентов и программа автоматического нахождения параметров”, Ж. вычисл. матем. и матем. физ., 2:1 (1962), 133–140
3. В. Я. Пан, “О способах вычисления значений многочленов”, УМН, 21:1(127) (1966), 103–134
4. В. Я. Пан, “О вычислении многочленов пятой и седьмой степени с вещественными коэффициентами”, Ж. вычисл. матем. и матем. физ., 5:1 (1965), 116–118
5. Пан В. Я. Некоторые схемы для вычисления значений полиномов с вещественными коэффициентами. Проблемы кибернетики. Вып. 5. М.: Наука, 1961, 17–29.
6. Белага Э. Г. О вычислении значений многочлена от одного переменного с предварительной обработкой коэффициентов. Проблемы кибернетики. Вып. 5. М.: Физматгиз, 1961, 7–15.

• многочлены
• полиномы
• вычисление многосленов
• схема Горнера
• схемы Пана

Источник: habr.com