Программа и схема вычисления

Схемы программ — это математические модели программ, описывающие строение программы, или точнее строение множества программ, где конкретные операции и функции заменены абстрактными функциональными и предикатными символами. Следующий пример программ вычисления факториала n! и переворачивания слов поясняет различие между программами и их схемойS1.

Функция CONSCARприписывает первую букву первого слова ко второму слову (т. е.CONSCAR(аб, в) = ав), а функцияCARстирает первую букву слова(т. е. CAR(аб) = б).

Базис класса стандартных схем программ

Стандартные схемы программ (ССП) характеризуются базисом и структурой схемы.

Базис класса фиксирует символы, из которых строятся схемы, указывает их роль (переменные, функциональные символы и др.), задает вид выражений и операторов схем.

Полный базис В класса стандартных схемсостоит из 4-х непересекающихся, счетных множеств символов и множества операторов — слов, построенных из этих символов.

Блок-схема программы для вычисления факториала

Множества символов полного базиса:

1. Х=x, х1, х2. у, у1 у2. z, z1, z2. >- множество символов, называемых переменными;

2. F=f (0) ,f (1) ,f (2) . g (0) ,g (1) ,g (2) . h (0) ,h (1) ,h (2) . >- множествофункциональных символов; верхний символ задаетместность символа; нульместные символы называют константами и обозначают начальными буквами латинского алфавитаa, b, c. ;

3. Р=р (0) ,р (1) ,р (2) . ;q (0) ,q (1) ,q (2) . ;>- множествопредикатных символов;р (0) ,q (0) — ; нульместные символы называют логическими константами;

Термами(функциональными выражениями) называются слова, построенные из переменных, функциональных и специальных символов по следующим правилам:

1.односимвольные слова, состоящие из переменных или констант, являются термами;

2.слово τ вида f ( n ) (τ1, τ2, . τn), где τ1, τ2, . τn- термы, является термом;

3.те и только те слова, о которых говорится в п.п. 1,2, являются термами.

Примеры термов: х, f (0) ,а,f (1) (х),g (2) (x, h (3) (y, a)).

Тестами (логическими выражениями)называются логические константы и слова видар ( n ) (τ1, τ2. τn). Примеры:p (0) ,p (0) (х),g (3) (x, y, z),p (2) (f (2) (x, y)). Допускается в функциональных и логических выражениях опускать индексы местности, если это не приводит к двусмысленности или противоречию.

Множество операторов включает пять типов:

1. начальный оператор- слово видаstart(х1, х2. хк), гдеk≥0, ах1, х2. хк — переменные, называемые результатом этого оператора;

2. заключительный оператор- слово видаstop(τ1, τ2. τn), где n≥ 0, а τ1, τ2. τn- термы; вхождения переменных в термы τ называютсяаргументамиэтогооператора;

3. оператор присваивания- слово видах:= τ, гдех– переменная (результат оператора), а τ — терм; вхождения переменных в термы называютсяаргументамиэтогооператора;

4. условный оператор (тест) — логическое выражение; вхождения переменных в логическое выражение называютсяаргументамиэтогооператора;

5. оператор петли- односимвольное словоloop.

Среди операторов присваивания выделим случаи: когда τ — переменная, то оператор называется пересылкой(х:=у) и когда τ — константа, то оператор называетсязасылкой(х:=а).

Подклассы используют ограниченные базисы. Так, например, подкласс V1имеет базис:х1, х2,а,f (1) ,p (1) , start, stop, (,),:=, ,и множество операторовstart(х1, х2);х1:=f(x1),x2:=f(x2),x1:=а,х2:= а, р(х1),р(х2),stop(х1, х2), т. е. схемы из этого подкласса используют две переменные, константу а, один одноместный функциональный символ, один предикатный символ и операторы указанного вида.

Источник: studfile.net

Что значит схема вычисления в математике

817. Найдите значения выражения, предварительно составив схему вычислений?

817. Найдите значения выражения, предварительно составив схему вычислений!

Напишите выражение по схеме рисунок 60 Составьте программу его вычисления и найдите его значение?

Напишите выражение по схеме рисунок 60 Составьте программу его вычисления и найдите его значение.

Проведи вычисления по схеме?

Проведи вычисления по схеме.

Заполни следующую схему данными так, чтобы по ней сформулировать задачу, которую можно решить с помощью произведения 350 х 3?

Заполни следующую схему данными так, чтобы по ней сформулировать задачу, которую можно решить с помощью произведения 350 х 3.

Для вычисления ответа этой задачи выполни умножение столбиком.

Составьте схему вычисления и найдите значение выражения 90 — 6×9?

Составьте схему вычисления и найдите значение выражения 90 — 6×9.

Найди шестую долю длины отрезка ?

Найди шестую долю длины отрезка .

Построй схему запиши вычисление

Запиши такие пропущенные цифры чтобы вычисление стало верным?

Запиши такие пропущенные цифры чтобы вычисление стало верным.

Выполни вычисления по алгоритму заданному блок схемой?

Выполни вычисления по алгоритму заданному блок схемой.

Сравни задания рассмотрим схемы?

Сравни задания рассмотрим схемы.

На этой странице сайта, в категории Математика размещен ответ на вопрос Что такое схема вычисления ?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Ответ : Пошаговое объяснение : Нехай швидкість 1ого мотоцикліста х, тоді швидк. 2гого = х + 10 км / год, запишемо рівняння : 220 = 2 * (× + × + 10) = 4х + 10 = 220 4х = 210 х = 52. 5 км / год ( швидкість1ого мотоцикліста) 52. 5 + 10 = 62. 5 км / ..

210 / 75 = 2, 8 2, 8 * 25 = 70 Вот и всё . Легко.

Неизвестное число = х ; 75% = 0, 75 часть числа х + 0, 75х = 210 1, 75х = 210 х = 210×1, 75 х = 120 Проверка : 0, 75х = 0, 75×120 = 90 120 + 90 = 210 210 = 210.

4) 9х + 19 = 64 9х = 64 — 29 9х = 45 х = 45 : 9 х = 5 5) 4, 5у + 2, 7 = 16, 2 4, 5у = 16, 2 — 2, 7 4, 5у = 13, 5 у = 13, 5 : 4, 5 у = 3 6) 4 1 / 2z + 7 / 9z + 2 1 / 3 + 1 / 6z = 5 1 / 18 9 / 2z + 7 / 9z + 7 / 3 + 1 / 6z = 5 1 / 18 (общий множитель — ..

А)доступное, маловероятно б)невозможное, нулевая вероятность в)случайное, достаточно вероятно г)доступное, стпроцентная вероятность.

Что бы разрезать эту фигуру на 2 равные части нужно сначала разрезать 2 квадрата по бокам, а потом разрезать один в середке на 2 половины.

Всего велосипедов 12. Если бы все были двухколесными, то колес было бы 24. А их на 3 больше. Значит трехколесных 3, а двухколесных 9.

1)12 * 2 = 24 2)27 — 24 = 3 ответ : 3 трехколесных велосипедов.

F(x) = 3x — 4 f'(x) = (3x)’ — 4′ = 3 — 0 = 3 Ответ : 3.

Что значит схема вычисления в математике

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

В этом уроке Вы познакомитесь с таким понятием как программа вычисления выражения, научитесь ее составлять и выполнять вычисления, следуя ее командам.

Каждое выражение задаёт программу своего вычисления. Она состоит из команд. Но чтобы правильно составить программу, необходимо четко знать три правила, которые определяют порядок выполнения действий при нахождении значений выражений.

Если в выражении нет скобок, и оно содержит действия только одной ступени, то есть только первой ступени: сложение и вычитание или только второй-умножение и деление, то их выполняют по порядку слева направо.

Если выражение содержит действия и первой, и второй ступеней и в нем нет скобок, то сначала выполняют действия второй ступени (то есть умножение и деление), а потом действия первой ступени – сложение и вычитание.

Если в выражении есть скобки, то сначала выполняют действия в скобках, учитывая при этом правила один и два.

Итак, давайте составим программу вычисления данного выражения:

Как видите, в выражении присутствуют скобки и есть действия и первой и второй ступеней. Воспользуемся правилами и начнем вычисление с первых скобок.

Команда 1: Перемножить числа 20 и 17.

Команда 2: Сложить число 300 с результатом команды 1.

Команда 3: Разделить 2052 на 38.

Команда 4: Вычесть из 134 результат команды 3.

Команда 5: Разделить результат команды 2 на результат команды 4.

Эту программу вычислений можно изобразить в виде схемы.

Последовательно выполнив действия, двигаясь по стрелочкам и заполнив пустые клетки, получим в нижней клетке ответ.

Давайте выполним все действия, согласно программе вычислений.

Первое действие: 20 умножить на 17, получится 340.

Второе действие: 300 плюс 340, будет 640.

Третье действие: 2052 разделить на 38, получится 54.

Четвертое действие: 134 минус 54, получится 80.

Пятое действие: 640 разделить на 80, будет 8.

Ответ: значение исходного выражения равно 8.

Таким образом, на этом уроке Вы познакомились с таким понятием как программа вычисления выражения, научились ее составлять и выполнять вычисления, следуя ее командам.

Порядок выполнения действий, правила, примеры

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Порядок вычисления простых выражений

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Условие: вычислите, сколько будет 7 − 3 + 6 .

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

Ответ: 7 − 3 + 6 = 10 .

Условие: в каком порядке нужно выполнять вычисления в выражении 6 : 2 · 8 : 3 ?

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Условие: подсчитайте, сколько будет 17 − 5 · 6 : 3 − 2 + 4 : 2 .

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6 : 3 − 2 + 4 : 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Условие: вычислите, сколько будет 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7 :

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · ( 2 + 3 ) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет ( 4 + ( 4 + ( 4 − 6 : 2 ) ) − 1 ) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6 : 2 = 4 − 3 = 1 , исходное выражение можно записать как ( 4 + ( 4 + 1 ) − 1 ) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению ( 4 + 5 − 1 ) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид ( 3 + 1 ) · 2 + 36 : 3 − 7 .

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13

Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Источник: remnabor.net

Алгоритмы. Алгоритм Евклида. Часть 1

Приветствуем читателей и посетителей нашего сайта! Сегодня на learnpascal.ru открывается новая рубрика — Алгоритмы. В этой рубрике мы с вами будем разбирать различные алгоритмы, а также их реализацию на Паскале.

Для освоения материала сегодняшнего урока вам понадобится знание циклов и ветвлений.

Сегодня мы рассмотрим три алгоритма(из пяти) на нахождение наибольшего общего делителя двух целых чисел, два из которых непосредственно связывают с именем Евклида. Еще два мы рассмотрим в следующей части.
Наибольший общий делитель (НОД) двух чисел a и b — наибольшее целое число, которое делит их оба.
Пример: НОД(25, 5) = 5; НОД(12, 18) = 6.

Переборный алгоритм

Начинаем перебор с d — наименьшего из двух чисел. Это первый, очевидный кандидат на роль их наибольшего общего делителя. А затем, пока d не делит оба числа, уменьшаем его на единицу. Как только такое деление будет обеспечено, останавливаем уменьшение d.

var a, b, d: integer; begin write(‘Введите два числа: ‘); readln(a, b); if a < b then d := a + 1 else d := b + 1; repeat d := d — 1 until (a mod d = 0) and (b mod d = 0); write(‘NOD = ‘, d) end.

Обратимся к этой программе, например, с числами 30 и 18. Тогда на пути к ответу(числу 6) ей придется перебрать числа: 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6.

Алгоритм Евклида «с вычитанием»

Пусть a и b — целые числа, тогда верны следующие утверждения:

1. Все общие делители пары a и b являются также общими делителями пары a — b, b;
2. И наоборот, все общие делители пары a — b и b являются также общими делителями пары a и b;
3. НОД(A, B) = НОД(A — B, B), если A > B;
4. НОД(A, 0) = A.

1. Если t — произвольный общий делитель a и b, то он делит и разность a — b. Действительно, из a = t * u и b = t * v следует, что a — b = t * u — t * v = t * (u — v). То есть t — также общий делитель а — b и b.
2. Обратно, если t — произвольный делитель общий делитель a — b и b, то он делит и их сумму a — b + b = a. Это можно доказать аналгично предыдущему. Поэтому t — также общий делитель a и b.
3. Делаем вывод, что множество общих делителей a и b совпадает с множеством делителей a — b и b. В частности, совпадают и наибольшие общие делители этих пар.
4. Наибольшее целое, на которое делится число a, есть само число а. Число 0 делится на любое число. Отсюда наибольший общий делитель а и 0 равен а.

Доказанная формула(3) позволяет свести вычисление наибольшего делителя одной пары к вычислению наибольшего общего делителя другой пары, в которой числа уже меньше. Очевидная же формула (4) дает нам понять, когда надо остановиться.

Вкратце алгоритм Евклида «с вычитанием» будет таким. Вычитаем из большего числа меньшее и заменяем большее на разность до тех пор, пока одно из чисел не обратится в нуль. Тогда оставшееся ненулевое число — наибольший общий делитель.

Пример. Пусть а = 82 и b = 60. НОД(82, 60) = НОД(22, 60) = НОД(22, 38) = НОД(22, 16) = НОД(6, 16) = НОД(6, 10) = НОД(6, 4) = НОД(2, 4) = НОД(2, 2) = НОД(2, 0) = 2.

На предпоследнем шаге алгоритма, перед появлением 0, оба числа равны, иначе не мог возникнуть 0. Поэтому мы будем извлекать НОД именно в этот момент.

Блок — схема алгоритма Евклида «с вычитанием»

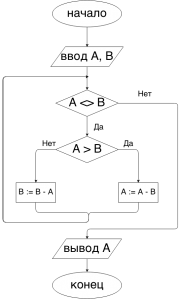
Программа

var a, b: integer; begin write(‘a = ‘); readln(a); write(‘b = ‘); readln(b); while a <> b do if a > b then a := a — b else b := b — a; writeln(‘NOD = ‘, a); end.

Алгоритм Евклида с «делением»

Пусть a и b — целые числа, а r — остаток от деления a на b. Тогда НОД(a, b) = НОД(b, r).

Эта формула также позволяет свести вычисление наибольшего общего делителя одной пары чисел к вычислению наибольшего обшего делителя другой пары чисел.

Пример. НОД(82, 60) = НОД(22, 60) = НОД(22, 16) = НОД(6, 16) = НОД(6, 4) = НОД(2, 4) = НОД(0, 2) = 2.

var a, b: integer; begin write(‘a = ‘); readln(a); write(‘b = ‘); readln(b); while (a <> 0) and (b <> 0) do if a >= b then a := a mod b else b := b mod a; write(a + b) end.

На сегодня все! Еще несколько модификаций алгоритма Евклида и способов нахождения НОД вы узнаете на следующих уроках.

Источник: learnpascal.ru