Cнова в школу! Лето неизбежно подходит к концу, и приходится восстанавливать в памяти подзабытые знания. Чтобы в новом учебному году грызть гранит науки было легче, мы представляем серию подборок, в которых описываем лучшие приложения для учёбы.
Часть 1: Математика.
_________________________________________________________________________________
MyScript Calculator [iOS, Android]
Разработчик: MyScript Цена: Бесплатно
Настоящую математику просто невозможно представить себе без расчётов. В трудных ситуациях под рукой должен быть калькулятор или даже лучше — мобильное приложение «MyScript Calculator» с рукописным вводом данных. Просто напишите на экране математическое выражение — и программа сделает всё остальное.
screen568x568
screen568x568
screen568x568
_________________________________________________________________________________
Геометрия Решебник и Теория [iOS, Android]
Разработчик: SO_RANDOM Цена: 39 руб. / 33 руб.
Название программы говорит само за себя — в ней есть всё, что может потребоваться учащемуся для занятий геометрией. Приложение даёт возможность повторить теорию, а также попрактиковаться в её применении.
ГЕОМЕТРИЯ 7 класса с нуля…ЭТО рвет любой урок в школе
screen568x568
screen568x568
screen480x480
_________________________________________________________________________________
Формулы [iOS, Android]
Разработчик: fabric17 Цена: Бесплатно
Это приложение поможет любому желающему запомнить сложные математические формулы по всем дисциплинам, будь то алгебра, геометрия, тригонометрия или что-нибудь другое. Более полного мобильного справочника практически не найти.
screen568x568
screen568x568
screen568x568
_________________________________________________________________________________
Algebra Course Assistant [iOS, Android]
Разработчик: fabric17 Цена: Бесплатно
Испытываете трудности с расчётами и вычислениями? Попробуйте это приложение — с ним вы забудете, что такое алгебраические сложности. А если понравится, можете приобрести ещё парочку других математических программ от того же разработчика.
screen568x568
screen568x568
screen568x568
_________________________________________________________________________________
Король математики [iOS, Android]
Разработчик: Oddrobo Software AB Цена: 66 руб.
Математика — это не только формулы и вычисления, это ещё и кропотливая работа мозга. В свободное от учёбы время вы можете интеллектуально потренировать свой мозг с приложением «Король Математики» и повысить навыки счёта в уме, что обязательно пригодится в будущем.
screen568x568
screen568x568
screen568x568
_________________________________________________________________________________
Новости партнеров
Новости партнеров
ferra.ru, 2023 г. 18+
Нашли опечатку? Выделите текст и нажмите Ctrl+Enter
Все права защищены. Полное или частичное копирование материалов Сайта в коммерческих целях разрешено только с письменного разрешения владельца Сайта. В случае обнаружения нарушений, виновные лица могут быть привлечены к ответственности в соответствии с действующим законодательством Российской Федерации.
Введение в геометрию (Математика) — Binogi Россия
Источник: www.ferra.ru
Программное обеспечение для решения геометрических задач
![]()
Wingeom возможности
- 1)создавать точные, аккуратные модели плоских и пространственных фигур: а) с использованием координат точек (вершин) фигуры; б) заданием готовых фигур; в) удалением элементов из готовой фигуры; г) добавлением элементов к готовой фигуре; д) создание сечений пространственных фигур.
- 2)трансформировать готовые изображения: а) способ изменения изображения (дискретный, непрерывный); б) вид изображения пространственных фигур (в центральной проекции, параллельной проекции, ортогональной проекции); в) перемещение фигуры (удаление, приближение, наклон, вращение, смещение); г) анимация;
- 3)редактировать построенные модели: а) выделять (толщина, цвет, стрелки, невидимые линии); б) удалять элементы (точки, линейные элементы, криволинейные элементы);
- 4)производить необходимые измерения: а) длина отрезка; б) величина угла в градусах; в) площадь многоугольника; г) периметр многоугольника; д) отношение длин отрезков; е) координаты точки; ж) величина двугранного угла;

- з) величина (в стерадианах) многогранного угла; и) длина дуги окружности; к) длина окружности; л) площадь круга, сечения многогранника; м) радианная мера угла; н) объем шара, конуса
- 5)применять геометрические преобразования: а) параллельный перенос; б) нормальный перенос; в) поворот; г) гомотетия; д) зеркальная симметрия; е) инверсия;
- 6)работать с текстом и обозначениями точек: а) ввод и удаление текста и обозначений; б) редактирование текста и обозначений (цвет, тип шрифта, размер шрифта); в) привязка текста (к фигуре, к рамке);
- 7)сохранять историю создания модели; 8)показать построение модели в медленном режиме (презентация); 9)использовать макрос (макро-построения).


- Категория: геометрическое ПО
- Язык программирования: Java
- Платформа (ОС): Windows, Linux, MacOS
- Название компании: Macrovision
- Лицензия: GPL (General Public License) свободно распространяемая лицензия
- Авторы: Markus Hohenwarter (Австрия, США),
- Сайт: http://www.geogebra.org/
- Язык интерфейса: русский
Систему можно использовать для построения линий:

- построение графиков функций y = f (x);
- построение конических сечений:
- коника произвольного вида — по пяти точкам.
- Окружность по центру и точке на ней, по центру и радиусу, по трем точкам;
- эллипс – по двум фокусам и точке на кривой;
- парабола – по фокусу и директрисе;
- гипербола – по двум фокусам и точке на кривой;
Кроме графических действий в системе могут быть выполнены вычисления:
- действия с матрицами: сложение, умножение; транспонирование, инвертирование; вычисление определителя;
- вычисления с комплексными числами;
- нахождение точек пересечения кривых;
- статистические функции:
- вычисление математического ожидания, дисперсии;
- вычисление коэффициента корреляции;
- Аппроксимация множества точек кривой заданного вида: полином; экспонента; логарифм; синусоида.
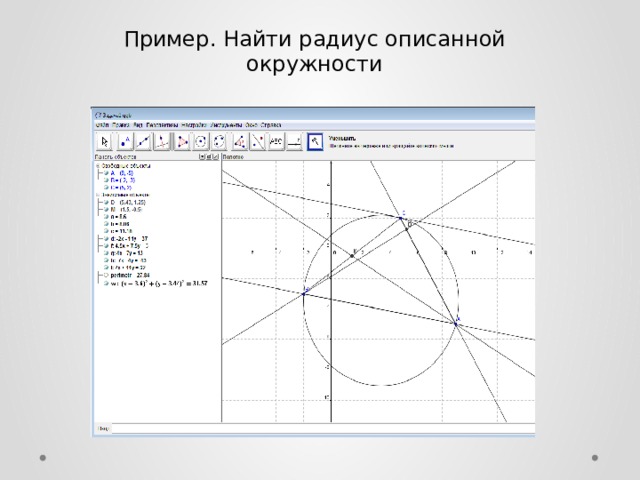
Пример. Найти радиус описанной окружности
«Живая геометрия»

- «Живая геометрия» — это набор инструментов, который предоставляет все необходимые средства для построения чертежей и их исследования. Она дает возможность «открывать» и проверять геометрические факты. Программа позволяет «оживлять» чертежи, плавно изменяя положение исходных точек.
- Слева расположен панель инструментов
- При помощи инструмента «точка» можно ставить различные точки.
- При помощи «циркуля» рисовать окружности разных размеров
- При помощи «линейка» можно размещать на чертеже линейные объекты: отрезки, лучи и другие прямые
- Инструмент «текст» позволяет создавать надписи на чертеже ,с его помощью так же можно давать имена геометрическим объектам
- С помощью «стрелки» можно передвинуть один объект или несколько элементов чертежа
- В Верхней части окна расположена строка мен.
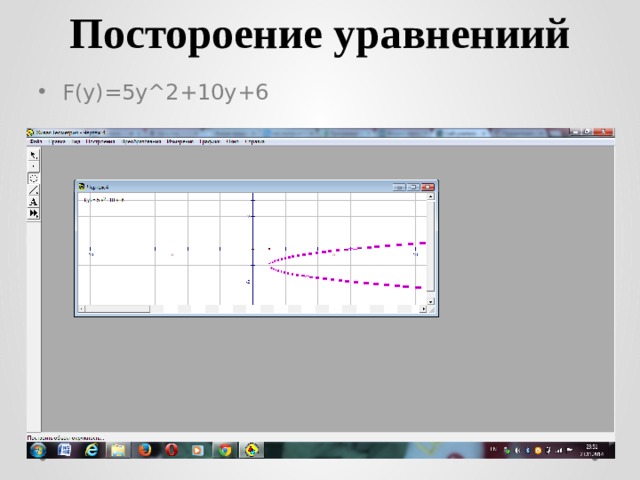
Постороение уравнениий

- F(y)=5y^2+10y+6
- Название программы: Poly
- Платформа (ОС): Windows
- Название компании: Pedagoguery Software
- Лицензия: условно бесплатная
- Сайт: http:// www.peda.com/poly
- Язык интерфейса: английский

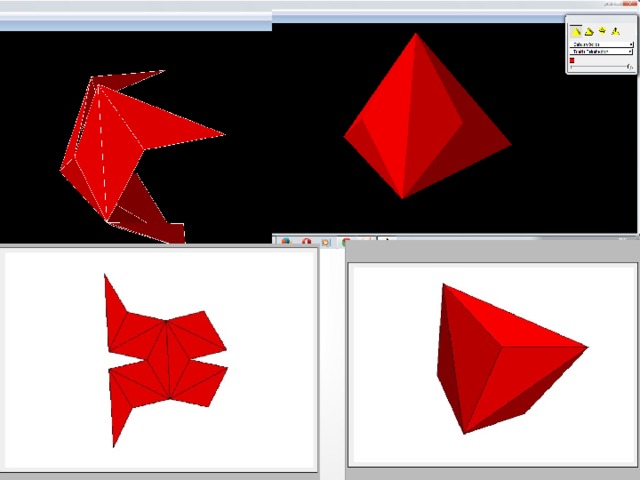
- Poly — программа для того, чтобы исследовать многогранные поверхности. Программа может показать многогранные поверхности тремя главными способами: • как трехмерное изображение, • как плоская, двумерная развертка, и • как топологическое вложение в плоскость.
- Трехмерные изображения могут в интерактивном режиме вращаться, сворачиваясь/разворачиваясь. Физические модели могут быть произведены, если распечатать плоские двумерные развертки, разрезать по периметру, свернуть по краям, и склеить лентой вместе соседние грани.
- Poly включает все особенности Poly и добавляет способность экспортировать многогранные модели, используя стандартные 3d форматы файлов (DXF, STL, 3DMF). С программой Pro Poly Вы можете также экспортировать вращающиеся многогранники как анимационные файлы GIF. Статические изображения могут экспортироваться как GIF или PCX файлы.
Источник: kopilkaurokov.ru
Материал по информатике на тему «Динамическая геометрия. Компьютерные программы по геометрии»
Динамическая геометрия – это программная среда, которая позволяет делать геометрические построения на компьютере таким образом, что при движении исходных объектов весь чертеж сохраняется.
Чумакова Ирина Александровна
Описание разработки
Динамическая геометрия – это программная среда, которая позволяет делать геометрические построения на компьютере таким образом, что при движении исходных объектов весь чертеж сохраняется.
Динамическая геометрия предназначена для создания интерактивных чертежей (моделей) по математике, сочетающих в себе конструирование, моделирование, динамическое варьирование, эксперимент.
Динамический наглядный конструктора предоставляет младшим школьникам возможность творческой манипуляции с объектами, а ученикам старшей школы – полнофункциональную среду для конструирования и решения задач.
Имеется целый ряд программ динамической геометрии, более или менее профессиональных, со своими преимуществами и недостатками.
При работе с программами динамической геометрии пользователь строит чертежи не на бумаге, а на экране компьютера. Когда пользователь строит чертеж в программе динамической геометрии, он фактический конструирует алгоритм построения. Построенный чертеж получается динамическим. Например: если пользователь правильно построил вписанную в треугольник окружность, она должна оставаться вписанной, даже если изменить форму треугольника, «потянув» за вершины. Такая устойчивость показывает, что построение верное.
Сильной стороной также является наличие операций трансформации (параллельный перенос, вращение, отражение, изменение пропорций), подобные операции отсутствуют в большинстве ИГС.
Программы динамической геометрии моделируют геометрическую среду, то есть, геометрические понятия и операции с ними. Интерфейсы современных инструментальных предметных программ создаются так, чтобы учесть сложившиеся традиции работы в этой предметной области. Поэтому работу с программой можно начинать не с чтения руководств, а с работы в этой среде. Разумеется, нужно быть знакомым с устройством стандартного графического интерфейса (например, Windows) и иметь навыки работы с мышкой (как сделать щелчок, двойной щелчок, как «схватить» объект и как «переместить» его и т. п. ).

К возможностям динамической геометрии относят:
— строить точки, прямые, лучи, отрезки, окружности;
— из этих фигур образовывать их комбинации – другие фигуры: углы, многоугольники, части круга и даже эллипсы с гиперболами и параболами;
— отмечать произвольную точку прямой, ломанной, окружности;
— строить отрезки и углы заданной величины;
— проводить прямые, перпендикулярные и параллельные данной, строить биссектрису угла;
— выполнять параллельный перенос, симметрии, поворот и гомотетию фигуры;
— деформировать фигуру или отдельные её части;
— вычислять длину отрезка, величину угла, периметр и площадь многоугольника, длину окружности и площадь круга (всё это приближённо);
— осуществлять анимации фигуры или отдельных её точек;
— выполнять итерацию с геометрическими и алгебраическими объектами.
Работа над динамической геометрией началась в 80-х годах с проекта Cabri (CAhier de BRouillon Informatique, Черновик для информатики), который предполагал создание среды для работы с объектами дискретной математики (графами, булевыми функциями).
Параллельно с развитием Cabri разрабатывалась и аналогичная программа The Geometer’s Sketchpad («Блокнот геометра»), которую создал в конце 80-х в США Nicholas Jackiw. Обладая очень удобным интерфейсом она быстро завоевала популярность учителей.
Полную информацию смотрите в файле.
Содержимое разработки
Динамическая геометрия
Динамическая геометрия – это программная среда, которая позволяет делать геометрические построения на компьютере таким образом, что при движении исходных объектов весь чертеж сохраняется.
Динамическая геометрия предназначена для создания интерактивных чертежей (моделей) по математике, сочетающих в себе конструирование, моделирование, динамическое варьирование, эксперимент.
Динамический наглядный конструктора предоставляет младшим школьникам возможность творческой манипуляции с объектами, а ученикам старшей школы – полнофункциональную среду для конструирования и решения задач.
Имеется целый ряд программ динамической геометрии, более или менее профессиональных, со своими преимуществами и недостатками.
При работе с программами динамической геометрии пользователь строит чертежи не на бумаге, а на экране компьютера. Когда пользователь строит чертеж в программе динамической геометрии, он фактический конструирует алгоритм построения. Построенный чертеж получается динамическим. Например: если пользователь правильно построил вписанную в треугольник окружность, она должна оставаться вписанной, даже если изменить форму треугольника, «потянув» за вершины. Такая устойчивость показывает, что построение верное.
Сильной стороной также является наличие операций трансформации (параллельный перенос, вращение, отражение, изменение пропорций), подобные операции отсутствуют в большинстве ИГС.
Программы динамической геометрии моделируют геометрическую среду, то есть, геометрические понятия и операции с ними. Интерфейсы современных инструментальных предметных программ создаются так, чтобы учесть сложившиеся традиции работы в этой предметной области. Поэтому работу с программой можно начинать не с чтения руководств, а с работы в этой среде. Разумеется, нужно быть знакомым с устройством стандартного графического интерфейса (например, Windows) и иметь навыки работы с мышкой (как сделать щелчок, двойной щелчок, как «схватить» объект и как «переместить» его и т.п.).
К возможностям динамической геометрии относят:
- строить точки, прямые, лучи, отрезки, окружности;
- из этих фигур образовывать их комбинации – другие фигуры: углы, многоугольники, части круга и даже эллипсы с гиперболами и параболами;
- отмечать произвольную точку прямой, ломанной, окружности;
- строить отрезки и углы заданной величины;
- проводить прямые, перпендикулярные и параллельные данной, строить биссектрису угла;
- выполнять параллельный перенос, симметрии, поворот и гомотетию фигуры;
- деформировать фигуру или отдельные её части;
- вычислять длину отрезка, величину угла, периметр и площадь многоугольника, длину окружности и площадь круга (всё это приближённо);
- осуществлять анимации фигуры или отдельных её точек;
- выполнять итерацию с геометрическими и алгебраическими объектами.

-80%
Источник: videouroki.net