Для реализации представленной математической модели в среде программирования необходимо составить алгоритм программы. В данном случае целесообразно использовать операторы множественного выбора, так как необходимо реализовать два направления моделирования — расчет и построение.
Приложение состоит из 4 блоков. Алгоритм главной формы представлен на листе 1 графической части.
Блок «Файл» даёт возможность создать новый файл, сохранить графическое представление построенной модели для дальнейшего использования посредствам команды «Открыть».
Для выполнения расчётов необходимо выполнить построение графа. Блок «Построение» предполагает визуальное представление графа с соответствующим заполнением переменных по ходу построения. Алгоритм подпрограммы «Построение» представлен в соответствии с листом 2 графической части.
Для построения модели графа необходимо сначала выбрать объект — узел, ребро. При построении узлов определяются названия городов, которые будут включены в имитационную модель сети передачи данных. А при проектировании рёбер определяются интенсивности пропускной способности для каждого населённого пункта.
// Современная криптография #2 // Blowfish //
После выбора объекта выбирается режим построения — добавить, выделить, удалить.
Блок «Расчёт» определяет параметры графа в соответствии с формулами (1) — (6), кратчайший путь в графическом и текстовом виде, реализованный по алгоритму Дейкстры, а также отчёт расчётов.
Отчёт результатов обобщает данные полученные на предыдущих шагах алгоритма и определяет параметры модели в виде таблиц, в которых зависимости от выбранного параметра может быть отражена информация о следующих результатах расчётов:
— время задержки пакетов в каналах между городами;
— интенсивность потока в каждом из узлов.
В алгоритме предусмотрено обращение в случае необходимости к справочной информации и руководству пользователя.
Также алгоритм спроектирован таким образом, что на любом этапе выполнения есть возможность прервать работу и выйти из проекта.
Реализация алгоритма программы на языке программирования
Алгоритм данной задачи реализован в среде объектно-ориентированного программирования Delphi.
Основные команды приложения лучше всего сделать доступными через пункты меню главного окна программы. Назначение пунктов меню можно пояснить в строке состояния главного окна. Нажатие на правую кнопку мыши сбрасывает выделение графа, кроме режима задания параметров узлов (в этом случае такая команда вызовет контекстное окно свойств для выбранной вершины).
Также необходимо обеспечить выполнение следующих команд.
Команды «Построение»приводит приложение в режим добавления узлов рёбер сети.
var i, j, cur_reb_stac1, cur_reb_stac2 : integer;
for i:= 1 to last_ver do
if i = cur_ver then Form1.Canvas.Pen.Color := clRed
else Form1.Canvas.Pen.Color := clBlack;
for i:= 1 to last_ver do
for j:= 1 to last_ver do
begin X1:= (usel[j].X — rad_ver);
Сложность алгоритмов и методы оптимизации программ
Y1:= (usel[j].Y — rad_ver);
ifkanal[i, j] > 0 then
if (i=cur_reb_p1) and (j=cur_reb_p2) then
else if (propusk[i,j].Intens>propusk[i,j].Traf) then
for i:= 1 to Count_p-1 do
begin Form1.Canvas.Pen.Color := clRed;
Команда «Расчеты — Подсчет параметров»рассчитывает матрицу вероятностей переходов графа, проверяет каждую дугу на стационарность (в случае нестационарности, соответствующая дуга может быть выделена цветом и выдавать предупреждение о неверности заданного параметра), а также рассчитывает веса существующих ребер. Результат на экране можно не отображать.
withRadioGroup1, StringGrid1 do
for i := 1 to last_ver do
1: begin //Пропускнаяспособность
for i := 1 to last_ver do
for j := 1 to last_ver do
2: begin //Время задержки пакетов в каналах между городами
GroupBox1.Caption:=’Время задержки пакетов в каналах между городами’;
for i := 1 to last_ver do
for j := 1 to last_ver do
3: begin //Интенсивность потока в каждом из узлов
GroupBox1.Caption:=’Интенсивность потока в каждом из узлов’;
for i := 1 to last_ver do
for j := 1 to last_ver do
Команда «Расчеты — Кратчайший путь». По данной команде программа вычисляет оптимальный путь между 0-й и последней вершиной при всех рассчитанных параметрах графа. Оптимальный путь целесообразно выделить на графе цветом.
//Кратчайший путь — алгоритм Дейкстры
procedure TForm1.N23Click(Sender: TObject);
if (ver_first < 1) or (ver_first>21) then ver_first := 1;
fillchar(Ras_Path,sizeof(Ras_Path), 10000); //бесконечность
Ras_Path[ver_first] := 0;//расстояние до начальной вершины
for i:=1 to 21 do
for j:=1 to 21 do
for j:=1 to 21 do
if ((propusk[v,j].Traf<>0) and (not versina[j]) and
and (ras_Path[j]<>0)) then p[j]:=p[j]+p[v]+’/’+inttostr(j)
for i := 1 to 21 do
if i=ver_last then p[i]:=inttostr(ver_first)+p[i]+’!’;
//—отображение на экране
S:=»; Count_p:=0; for i:=1 to length(p[ver_last]) do
if (copy(p[ver_last],i,1)=’/’) or (copy(p[ver_last],i,1)=’!’) then
// Вывод перечень вершин пути
for i:=1 to Count_p-1 do
Memo1.Text := Memo1.Text + IntToStr(krat_put[i]) + ‘-‘;
Memo1.Text := Memo1.Text + IntToStr(krat_put[Count_p]);
for i := 1 to Count_p do
Path := Path + ras_Path[krat_put[i]];
for i:= 1 to Count_p-1 do
begin Form1.Canvas.Pen.Color := clRed;
Команда «Расчеты — Отчет». Выводит на экран модальное окно, содержащее в себе отчет по рассчитанным параметрам модели в текстовом виде (время задержки в каждой дуге, интенсивность прихода заявок в каждый узел, а также метки вершин).
procedure TForm1.N20Click(Sender: TObject);
var i,j, cur_reb_stac1, cur_reb_stac2 : integer;
for i:=1 to 21 do
for j:=1 to 21 do
usel[i].TrafOut := usel[i].TrafOut + propusk[i,j].Traf;
for i:=1 to 21 do
for j:=1 to 21 do
//интенсивность канала и число пакетов поступающих в город
for i:=1 to 21 do
for j:=1 to 21 do
for i:=1 to last_ver do
For j:=1 to last_ver do
beginshowmessage(‘Необходимо увеличить пропускную способность канала между городами : ‘+usel[i].Name + ‘ и ‘ + usel[j].Name);
//расчет задержек в ребрах
for i:=1 to 21 do
for j:=1 to 21 do
if (propusk[i,j].Traf<> 0) then begin
ifpropusk[i,j].Traf — propusk[i,j].Intens = 0
thenpropusk[i,j].Traf := propusk[i,j].Traf + 1;
Команда «Файл — Новый» осуществляет создание нового пустого документа модели сети передачи данных.
//Создание нового файла
procedure TForm1.N6Click(Sender: TObject);
Источник: studbooks.net
Алгоритмизация. Введение в язык программирования С++ — тест 3
nbsp
nbsp
nbsp
nbsp
Упражнение 8: Номер 1
Выберите варианты записи строк для данной части блок-схемы: 
nbsp
nbsp
nbsp
nbsp
nbsp
Номер 2
Выберите вариант записи строк для данной части блок-схемы: 
nbsp
nbsp
nbsp
nbsp
Номер 3
Какая часть блок-схемы подходит для данного участка кода? 
nbsp
nbsp
Источник: eljob.ru
1.4 Реализация алгоритмов
После того, как алгоритм разработан, его необходимо реализовать посредством языка программирования. Рассмотрим примеры наиболее распространенных алгоритмов для решения задач.
1.4.1 Простые алгоритмы
Рассмотрим алгоритм нахождения наибольшего из трех чисел.
Введем обозначение для «наибольшего» как max. В результате выполнения сравнений a и b, a и c, далее b и a, b и c, c и a, c и b – получим всего три альтернативных варианта выбора решения, в каждом из которых присутствует одна из трех исходных величин.
Составим словесный алгоритм.
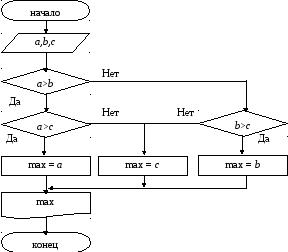
- Ввести a, b, c.
- Если a>b и a>c, то max = a.
- Если b>a и b>c, то max = b
- Если c>a и c>b, то max = c
- Вывод max
- Конец
1.4.2 Рекурсивные алгоритмы
- условие для завершения цикла;
- тело рекурсии, которое включает действия, предназначенные для выполнения на каждой итерации;
- шаг рекурсии, на котором рекурсивный алгоритм вызывает сам себя.
1.4.3 Циклические алгоритмы
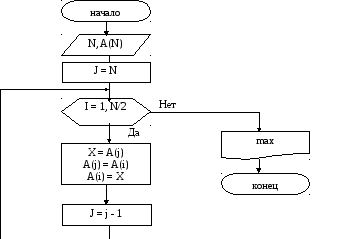
Рассмотрим задачу расположения элементов заданного массива в обратном порядке. Назовем исходный массив как массив A(N), в котором N элементов. При составлении алгоритма можно использовать тот же исходный массив A и выполнять на каждом шаге «переприсвоение» элементов массива из верхней части элементам нижней части и наоборот, т.е. осуществить некоторый двусторонний обмен. Фрагмент программы для реализации алгоритма: J := N; For I:= 1 to N/2 Do Begin X: = a(j); a(j): = a(i); a(i): = x; J: = j – 1; End; Writeln(‘Max=’, max);
1.4.4 Алгоритмы поиска данных
Задача поиска заключается в отыскании в заданной последовательности элемента или нескольких элементов с заданными свойствами. Существует несколько основных вариантов организации поиска данных: А) Поиск номера элемента последовательности с заданным значением. В) Поиск максимального или минимального элемента и его номера в заданной последовательности.
Задачу А можно назвать основной задачей, а задачу В – производной от А. Последовательность для поиска может быть как упорядоченная, так и неупорядоченная. Примем следующее допущение. Пусть задана определенная последовательность данных i> = X1, X2,…,XN, где I изменяется от 1 до N, длина N которой является фиксированной величиной.
Все элементы имеют разные значения. Необходимо найти некоторый заданный элемент. Алгоритм поиска имеет аргумент Р и заключается в нахождении записи, для которой Р служит некоторым признаком поиска или ключом Р. Результатом поиска может быть одно из двух: либо поиск завершился успешно и запись, которая содержит Р, найдена, либо поиск оказался неудачным и запись не найдена.
Поиск номера элемента последовательности с заданным значением. По условию поиска для некоторой исходной последовательности необходимо определить номер элемента, значение которого равно значению заданной переменной Р. Другой информацией об элементе мы не располагаем, поэтому очевиден простой линейный просмотр или последовательный перебор элементов массива.
В этом случае поиск повторяется до тех пор, пока не будет найден нужный элемент последовательности, равный некоторому эталону Р. Особенностями такого поиска являются: – независимость поиска; – цикличность поиска – количество повторений не превышает количество элементов в заданной последовательности; – простота реализации алгоритма. Условиями окончания процесса поиска являются: – элемент найден, т.е.
Р = Xi; – элемент не найден, хотя массив просмотрен от начала до конца, но при этом совпадений не было. Если элемент будет найден, то индекс найденного элемента будет минимально возможным. Но в заданной последовательности может не оказаться элемента со значением.
Если предполагается, что в исходной последовательности может быть только один элемент, равный эталону, то, после того, как этот элемент найден, поиск можно закончить. Если таких элементов имеется несколько, то можно задать дополнительное условие, какой по порядку найденных необходим элемент.
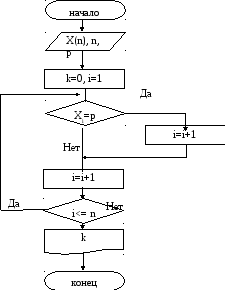
В последнем случае задается дополнительная переменная, которая будет подсчитывать количество элементов, равных эталону Р. Основной алгоритм поиска будет следующим: 1. сравнить очередной элемент с переменной Р. 2. перейти к следующему элементу. 3. если не все элементы просмотрены, повторить, начиная с п. 1. Алгоритм должен однозначно реагировать на ситуацию, если искомого значения в последовательности нет.
Для этой цели вводится в алгоритм переменная k, начальное значение которой равно 0. Результат k>0 – номер найденного элемента. Если элемент со значением Р не найден, то результат k остается нулевым. Эффективность поиска прямо пропорциональна количеству вычислений. Алгоритм поиска в упорядоченной последовательности.
Если последовательность упорядочена, т.е. значения элементов последовательности возрастают или убывают с увеличением порядковых номеров элементов, то к ней есть возможность применить другой алгоритм поиска. Стандартным методом поиска в упорядоченном массиве является метод деления отрезка пополам (алгоритм дихотомии).
В процессе такого поиска границы промежутка можно сдвинуть друг к другу. После каждого сравнения сдвигается верхняя, либо нижняя граница промежутка.
Промежутком данных или отрезком является отрезок индексов от 1 до N. Пусть значение наименьшего индекса в исходной последовательности равно А, а значение наибольшего индекса – В. Если разделить рассматриваемый интервал [A,B] пополам, получится некоторое значение С. Сравниваем X[C] с заданным значением Р. Если X[C]>P, то элемент следует искать для B = C – 1, если X[C]Алгоритм вычисления суммы положительных чисел в таблице Tabl(5,5). Рассмотрим пример как типичную задачу – поиск; в данном случае следует найти сумму чисел, значение которых больше нуля.
Необходимо выполнить сравнение «Если Tabl(i,j)>0» для 25 вводимых чисел. Иначе – сравнение для 5 строк по 5 столбцам. Имеем два вложенных цикла. Первым будет цикл по строкам – по i, вложенным по отношению к нему является цикл по столбцам – по j. Величина суммы вычисляется накоплением от начального задания СумП=0.
Далее сумма увеличивается на величину, равную следующему по порядку элементу матрицы, – всего 25 увеличений. Словесное описание алгоритма вычисления суммы положительных элементов в таблице имеет следующий вид: 1. СумП=0. 2. номер строки i=1.
3. номер столбца j=1 4. ввести элемент таблицы Tabl(i,j) 5. Если Tabl(i,j)>0, то СумП = СумП + Tabl(i,j) 6. следующий элемент столбца j = j+1 7. Все элементы столбца просмотрены? Если jАлгоритм, подсчитывающий количество чисел в массиве. Рассмотрим на примере: Дана таблица А, в которой 100 целых чисел. Требуется найти все числа, значение которых = 25. Найти их количество. Составить алгоритм.
Обозначим количество – k, начальное значение k=0. Эта величина в отличие от суммы всегда должна иметь целый тип и всегда одно и то же правило изменения, если не задано дополнительных условий. Если сравнение на совпадение A(i) и числа 25 истинно, то количество должно увеличиваться на 1. Алгоритм поиска в тексте заданного символа. Задан текст.
Найти, содержится ли в данном тексте некоторый заданный символ и сколько раз он повторяется. Имеем текст или некоторую последовательность символов, которая является исходной. Назовем эту последовательность Slovo, каждый символ этой последовательности равен i, т.е. – это номер позиции, в которой находится символ.
Также имеется заданный символ (или строка символов), с которым будем сравнивать исходную последовательность. Символ обозначим S1. Длину символьной последовательности можно определить как некоторое вычисляемое N, – средства языка программирования позволяют это сделать.
Строка фактически является массивом символов, в котором с каждым символом строки ассоциируется уникальное значение символа. Обратиться к отдельному элементу строки внутри символьной переменной можно с помощью выражения: имя строки [i]>, где i – индекс символа, на который ссылается алгоритм. Значение индекса первого элемента равно 1, второго – 2 и т.д.
Для определения количества найденных символов, равных S1, введем переменную k1. Переменная k необходима для обозначения номера позиции, в которой найден символ S1. В схеме алгоритма удобно реализовать циклическую структуру с предусловием – пока номер позиции символа в рассматриваемой последовательности меньше длины всей последовательности.
Если найдено совпадение в какой-то позиции символа с S1, то этот найденный номер позиции увеличивается на 1, т.е. переходим к рассмотрению следующего символа позиции.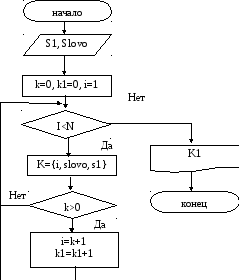 
Алгоритм нахождения самого длинного слова. Допустим, имеется некоторый текст Frag, переменная типа строка String неизвестной длины.
Чтобы выделить слова в тексте, необходимо выделить пробелы между словами – количество пробелов равно количеству слов минус 1. обозначим массив слов как Slovo, тип – строка String. Введем символическое ограничение не более 10 знаков в слове, в тексте не более 100 слов или не более 256 знаков. Определим словесный алгоритм. 1. Ввод текста. 2. Выделить слова в тексте в массив слов.
3. Найти самое длинное слово. Для последнего пункта можно использовать стандартный алгоритм поиска в заданной последовательности. В данном случае последовательность будет состоять из массива Slovo(1), Slovo(2),…, который можно определить, если решить следующие задачи: 1) Выделить пробел n. 2) Определить количество выделенных слов m. 3) Определить отдельное словj в массив слов Slovo(m). 4) Повторить с п.1, пока не достигли конца текста.
Источник: studfile.net