В этом руководстве мы узнаем об алгоритме имитации отжига и покажем пример реализации, основанный на задаче коммивояжера (TSP).
2. Имитация отжига
Алгоритм имитации отжига — это эвристика для решения задач с большим пространством поиска.
Вдохновение и название пришли из отжига в металлургии; это метод, который включает нагрев и контролируемое охлаждение материала.
В общем, имитация отжига снижает вероятность принятия худших решений, поскольку исследует пространство решений и снижает температуру системы. Следующая анимация показывает механизм поиска наилучшего решения с помощью алгоритма имитации отжига:
Как видим, алгоритм использует более широкий диапазон решений при высокой температуре системы, ища глобальный оптимум. При понижении температуры диапазон поиска становится меньше, пока не будет найден глобальный оптимум.
Алгоритм имеет несколько параметров для работы:
- количество итераций — условие остановки для моделирования
- начальная температура – начальная энергия системы
- параметр скорости охлаждения — процент, на который мы снижаем температуру системы
- минимальная температура – опциональное условие остановки
- время симуляции – необязательное условие остановки
Значения этих параметров должны быть тщательно выбраны, так как они могут иметь существенное влияние на производительность процесса.
Решение задачи коммивояжера с помощью библиотеки python-tsp
3. Задача коммивояжера
Задача коммивояжера (TSP) — самая известная в современном мире задача оптимизации информатики.
Проще говоря, это задача поиска оптимального маршрута между узлами в графе. Общее расстояние перемещения может быть одним из критериев оптимизации. Для получения более подробной информации о TSP, пожалуйста, посмотрите здесь .
4. Java-модель
Чтобы решить задачу TSP, нам понадобятся два класса моделей, а именно City и Travel . В первом мы будем хранить координаты узлов графа:
Конструктор класса City позволяет нам создавать случайные расположения городов. Логика DistanceToCity(..) отвечает за расчеты расстояния между городами.
Следующий код отвечает за моделирование тура коммивояжера. Начнем с генерации начального порядка городов в путешествии:
public void generateInitialTravel() if (travel.isEmpty()) new Travel(10); > Collections.shuffle(travel); >
В дополнение к генерации начального порядка нам нужны методы для замены двух случайных городов в порядке следования. Мы будем использовать его для поиска лучших решений внутри алгоритма имитации отжига:
public void swapCities() int a = generateRandomIndex(); int b = generateRandomIndex(); previousTravel = new ArrayList>(travel); City x = travel.get(a); City y = travel.get(b); travel.set(a, y); travel.set(b, x); >
Кроме того, нам нужен метод для отмены генерации свопа на предыдущем шаге, если новое решение не будет принято нашим алгоритмом:
public void revertSwap() travel = previousTravel; >
Последний метод, который мы хотим охватить, — это расчет общего расстояния перемещения, которое будет использоваться в качестве критерия оптимизации:
Решение задачи коммивояжера. Метод ветвей и границ.
public int getDistance() int distance = 0; for (int index = 0; index travel.size(); index++) City starting = getCity(index); City destination; if (index + 1 travel.size()) destination = getCity(index + 1); > else destination = getCity(0); > distance += starting.distanceToCity(destination); > return distance; >
Теперь давайте сосредоточимся на основной части, реализации алгоритма имитации отжига.
5. Имитационная реализация отжига
В следующей реализации имитации отжига мы собираемся решить проблему TSP. Напомню, что цель состоит в том, чтобы найти кратчайшее расстояние для путешествия по всем городам.
Чтобы запустить процесс, нам нужно указать три основных параметра, а именно : startTemperature , numberOfIterations и coolRate :
public double simulateAnnealing(double startingTemperature, int numberOfIterations, double coolingRate) double t = startingTemperature; travel.generateInitialTravel(); double bestDistance = travel.getDistance(); Travel currentSolution = travel; // . >
Перед началом моделирования мы генерируем начальный (случайный) порядок городов и вычисляем общее расстояние для проезда. Поскольку это первое рассчитанное расстояние, мы сохраняем его в переменной bestDistance вместе с currentSolution.
На следующем шаге мы запускаем основной цикл моделирования:
for (int i = 0; i numberOfIterations; i++) if (t > 0.1) //. > else continue; > >
Цикл будет длиться указанное нами количество итераций. Более того, мы добавили условие остановки симуляции, если температура будет ниже или равна 0,1. Это позволит нам сэкономить время моделирования, так как при низких температурах различия в оптимизации почти не видны.
Давайте посмотрим на основную логику алгоритма имитации отжига:
currentSolution.swapCities(); double currentDistance = currentSolution.
getDistance(); if (currentDistance bestDistance) bestDistance = currentDistance; > else if (Math.exp((bestDistance — currentDistance) / t) Math.random()) currentSolution.revertSwap(); >
На каждом шаге моделирования мы случайным образом меняем местами два города в порядке следования.
Кроме того, мы вычисляем currentDistance . Если вновь вычисленное значение currentDistance меньше значения bestDistance , мы сохраняем его как лучшее.
В противном случае мы проверяем, не меньше ли функция распределения вероятностей Больцмана, чем случайно выбранное значение в диапазоне от 0 до 1. Если да, то отменяем обмен городами. Если нет, сохраняем новый порядок городов, так как это может помочь нам избежать локальных минимумов.
Наконец, на каждом этапе симуляции мы уменьшаем температуру на заданную скорость охлаждения:
t *= coolingRate;
После симуляции мы возвращаем лучшее решение, найденное с помощью Simulated Annealing.
Обратите внимание на несколько советов о том, как выбрать наилучшие параметры моделирования:
- для небольших пространств решения лучше понизить начальную температуру и увеличить скорость охлаждения, так как это сократит время моделирования без потери качества
- для больших объемов решения выберите более высокую начальную температуру и меньшую скорость охлаждения, так как будет больше локальных минимумов
- всегда предоставляйте достаточно времени для имитации перехода от высокой к низкой температуре системы
Не забудьте потратить некоторое время на настройку алгоритма с меньшим экземпляром задачи, прежде чем приступить к основному моделированию, так как это улучшит окончательные результаты. На примере алгоритма Simulated Annealing была показана настройка в этой статье .
6. Заключение
В этом кратком руководстве мы смогли узнать об алгоритме имитации отжига и решили задачу коммивояжера . Мы надеемся, что это показывает, насколько удобен этот простой алгоритм применительно к определенным типам задач оптимизации.
Полную реализацию этой статьи можно найти на GitHub .
Источник: for-each.dev
Задача коммивояжера методом Литтла на C++
Обучаясь в университете, каждому приходилось делать разного рода задачи. Вот, наступает конец полугодия, сессия на носу, начало выдачи курсовых заданий и мне посчастливилось стать тем, кто должен реализовать метод Литтла для задачи коммивояжера. Итак начнем.
Кто такой коммивояжер? Коммивояжер — это разъездной торговый агент какой-либо фирмы, предлагающий покупателям товары по образцам и каталогам. Его задача объездить все пункты назначения, не побывав ни в одном дважды и вернуться в точку старта.

Метод Литтла
Целью данного метода является поиск гамильтонового цикла с минимальной стоимостью в графе. Что бы найти его, нужно придерживаться следующим действиям:
- В каждой строке матрицы стоимости найдем минимальный элемент и вычтем его из всех элементов строки. Сделаем это и для столбцов, не содержащих нуля. Получим матрицу стоимости, каждая строка и каждый столбец которой содержат хотя бы один нулевой элемент.
- Для каждого нулевого элемента матрицы, рассчитываем коэффициент k, который равен сумме минимальных элементов столбца и строки этого нуля. Выбираем нуль с максимальным коэффициентом (если таковых несколько выбираем любой из них). Вносим в гамильтонов контур соответствующую дугу.
- Удаляем строку и столбец, на пересечении которого выбранный нами нуль.
- Проверяем граф на наличие точек возврата, если есть таковые, то меняем их значение на максимальное. Повторяем предыдущие действия пока не останется матрица порядка 2.
- Вносим в гамильтонов контур недостающие дуги. Получаем искомый цикл.
Реализация
Для дальнейшего расширения и работы с другими алгоритмами, создадим класс Algorithm:
Algorithm
//Algorithm.h class Algorithm < public: char* name = «Algorithm»; // Название алгоритма std::vector> data; // Массив значений (матрица) Algorithm(); Algorithm(std::vector>); Algorithm(char*); bool LoadData(std::vector>); bool LoadData(char*); virtual void Run(); // Метод для запуска алгоритма protected: int GetStrCount(std::ifstream // Считываем количество строк в файле int GetColCount(std::ifstream // Считываем количество столбцов в файле virtual bool validateData(); // Метод для проверки значений в матрице. Вызывается перед Run() >;
Как видно выше, здесь будут реализованы методы для загрузки данных из файла и вручную. Их реализацию можно посмотреть в приложении.
Далее, создадим класс интересующего нам алгоритма. В нашем случае LittleAlgorithm.
LittleAlgorithm
class LittleAlgorithm : public Algorithm < public: vector> result; // Результат. Здесь будет храниться искомый цикл LittleAlgorithm(); LittleAlgorithm(vector>); LittleAlgorithm(char*); virtual void Run(); private: enum check; int getMin(vector>, int, check); // Поиск минимального элемента столбца/строки void matrixProcedure(vector>); // Метод в котором идет поиск цикла void showMatrix(vector>); // Вывод матрицы int getResultSum(); // Считывание суммы всех выбранных дуг virtual bool validateData(); >;
Реализация вспомогательных методов:
void LittleAlgorithm::Run() < name = «Little algorithm»; Algorithm::Run(); matrixProcedure(vector>(data)); > int LittleAlgorithm::getMin(vector> matrix, int sel, check pos) < int min = INT32_MAX; for (int i = 0; i < matrix[sel].size() — 1; i++) switch (pos) < case LittleAlgorithm::Row: if (min >matrix[sel][i]) min = matrix[sel][i]; break; case LittleAlgorithm::Col: if (min > matrix[i][sel]) min = matrix[i][sel]; break; > return min; > void LittleAlgorithm::showMatrix(vector> temp) < std::cout std::cout std::cout int LittleAlgorithm::getResultSum() < int sum = 0; for (int i = 0; i < result.size(); i++) sum += data[result[i].first — 1][result[i].second — 1]; return sum; >bool LittleAlgorithm::validateData() < //Добавляем в нашу матрицу столбец и строку с нумерацией для отслеживания удаляемых ребер for (int i = 0; i < data.size(); i++) for (int j = 0; j < data[i].size(); j++) if (data[i][j] == 0) data[i][j] = INT32_MAX; vector> temp(data); for (int i = 0; i < data.size(); i++) data[i].push_back(i + 1); vectornumeration; for (int i = 0; i
А вот и собственно говоря сам метод, реализующий метод Литтла:
matrixProcedure
void LittleAlgorithm::matrixProcedure(vector> matrix) < //Определяем точку возврата и удаляем необходимое ребро if (matrix.size() — 1 >2) < vectorvertexes; for (int i = 0; i < result.size(); i++) < vertexes.push_back(result[i].first); vertexes.push_back(result[i].second); >for (int i = 0; i < vertexes.size(); i++) < pairelem(INT32_MAX, INT32_MAX), elem1(INT32_MAX, INT32_MAX); for (int j = 0; j < vertexes.size(); j++) < if (vertexes[i] != vertexes[j]) < for (int k = 0; k < matrix[matrix.size() — 1].size() — 1; k++) < if (vertexes[i] == matrix[k][matrix[k].size() — 1]) elem.first = k; if (vertexes[j] == matrix[k][matrix[k].size() — 1]) elem1.first = k; >for (int k = 0; k < matrix.size() — 1; k++) < if (vertexes[i] == matrix[matrix.size() — 1][k]) elem.second = k; if (vertexes[j] == matrix[matrix.size() — 1][k]) elem1.second = k; >> > for (int i = 0; i < matrix.size() — 1; i++) for (int j = 0; j> //Вычитаем из каждой строки минимальное значение for (int i = 0; i < matrix.size() — 1; i++) < int min = 0; if ((min = getMin(matrix, i, check::Row)) == INT32_MAX) < showMatrix(matrix); std::cout if ((min = getMin(matrix, i, check::Row)) != 0) for (int j = 0; j < matrix[i].size() — 1; j++) if(matrix[i][j] != INT32_MAX) matrix[i][j] -= min; >//Вычитаем из каждого столбца минимальное значение for (int i = 0; i < matrix[matrix.size() — 1].size() — 1; i++) < int min = 0; if ((min = getMin(matrix, i, check::Col)) == INT32_MAX) < showMatrix(matrix); std::cout if ((min = getMin(matrix, i, check::Col)) != 0) for (int j = 0; j < matrix.size() — 1; j++) if (matrix[j][i] != INT32_MAX) matrix[j][i] -= min; >//Находим максимально оцененный ноль int Max = 0; for (int i = 0; i < matrix.size() — 1; i++) for (int j = 0; j < matrix[i].size() — 1; j++) if (matrix[i][j] == 0) < matrix[i][j] = INT32_MAX; int max = (getMin(matrix, i, check::Row) == INT32_MAX || getMin(matrix, j, check::Col) == INT32_MAX)? INT32_MAX: getMin(matrix, i, check::Row) + getMin(matrix, j, check::Col); if (max >Max) Max = max; matrix[i][j] = 0; > //Находим все нули максимальная оценка которых равна Max vector Maxs; for (int i = 0; i < matrix.size() — 1; i++) for (int j = 0; j < matrix[i].size() — 1; j++) if (matrix[i][j] == 0) < matrix[i][j] = INT32_MAX; int max = (getMin(matrix, i, check::Row) == INT32_MAX || getMin(matrix, j, check::Col) == INT32_MAX) ? INT32_MAX : getMin(matrix, i, check::Row) + getMin(matrix, j, check::Col); if (max == Max) Maxs.push_back(pair(matrix[i][matrix.size() — 1], matrix[matrix.size() — 1][j])); matrix[i][j] = 0; > //Вывод координат выбранных нулей std::cout for (int i = 0; i < Maxs.size(); i++) < //Добавляем вершину в массив с результатом result.push_back(Maxs[i]); //Если размер матрицы порядка 1, выводим результат и завершаем текущию ветвь if (matrix.size() — 1 == 1) < for (int i = 0; i < result.size(); i++) std::cout //Создаем копию текущей матрицы и удаляем из нее строку и столбец выбранного нуля vector> temp(matrix); pair elem(INT32_MAX, INT32_MAX), elem1(INT32_MAX, INT32_MAX); for (int j = 0; j < temp[temp.size() — 1].size() — 1; j++) < if (Maxs[i].first == temp[j][temp[j].size() — 1]) elem.first = j; if (Maxs[i].second == temp[j][temp[j].size() — 1]) elem1.first = j; >for (int j = 0; j < temp.size() — 1; j++) < if (Maxs[i].second == temp[temp.size() — 1][j]) elem.second = j; if (Maxs[i].first == temp[temp.size() — 1][j]) elem1.second = j; >for(int i = 0; i < temp.size() — 1; i++) for(int j = 0;j>
Результат
К примеру для матрицы:
0 5 8 10 0 0 3 6
5 0 2 0 0 0 0 1
8 2 0 4 5 6 0 7
10 0 4 0 12 9 7 0
0 0 5 12 0 9 0 12
0 0 6 9 9 0 8 0
3 0 0 7 0 8 0 2
6 1 7 0 12 0 2 0
Результатом будет:
Результат
Little algorithm:
Maxs — 1 7 7 1
1 2 3 4 5 6 7 8
______________________________________________________
1 | inf 2 5 5 inf inf 0 3
2 | 3 inf 1 inf inf inf inf 0
3 | 5 0 inf 0 0 0 inf 5
4 | 5 inf 0 inf 5 1 3 inf
5 | inf inf 0 5 inf 0 inf 7
6 | inf inf 0 1 0 inf 2 inf
7 | 0 inf inf 3 inf 2 inf 0
8 | 4 0 6 inf 8 inf 1 inf
1 2 3 4 5 6 8
________________________________________________
2 | 0 inf 1 inf inf inf 0
3 | 2 0 inf 0 0 0 5
4 | 2 inf 0 inf 5 1 inf
5 | inf inf 0 5 inf 0 7
6 | inf inf 0 1 0 inf inf
7 | inf inf inf 3 inf 2 0
8 | 1 0 6 inf 8 inf inf
1 2 3 4 5 6
__________________________________________
2 | 0 inf 1 inf inf inf
3 | 2 0 inf 0 0 0
4 | 2 inf 0 inf 5 1
5 | inf inf 0 5 inf 0
6 | inf inf 0 1 0 inf
8 | inf 0 6 inf 8 inf
1 3 4 5 6
____________________________________
2 | inf 0 inf inf inf
3 | 0 inf 0 0 0
4 | 0 0 inf 5 1
5 | inf 0 5 inf 0
6 | inf 0 1 0 inf
1 4 5 6
______________________________
3 | inf 0 0 0
4 | 0 inf 5 1
5 | inf 5 inf 0
6 | inf 1 0 inf
4 5 6
________________________
3 | inf 0 0
5 | 4 inf 0
6 | 0 0 inf
4 5
__________________
3 | inf 0
6 | 0 inf
(1, 7) (7, 8) (8, 2) (2, 3) (4, 1) (5, 6) (3, 5) (6, 4)
Result: 41
Maxs — 3 5
(1, 7) (7, 8) (8, 2) (2, 3) (4, 1) (5, 6) (6, 4) (3, 5)
Result: 41
Maxs — 3 5 5 6
5 6
__________________
3 | 0 0
5 | inf 0
(1, 7) (7, 8) (8, 2) (2, 3) (4, 1) (6, 4) (3, 5) (5, 6)
Result: 41
Maxs — 3 5
(1, 7) (7, 8) (8, 2) (2, 3) (4, 1) (6, 4) (5, 6) (3, 5)
Result: 41
Maxs — 2 8
2 3 4 5 6 7 8
________________________________________________
1 | 0 3 3 inf inf inf 1
2 | inf 1 inf inf inf inf 0
3 | 0 inf 0 0 0 inf 5
4 | inf 0 inf 5 1 2 inf
5 | inf 0 5 inf 0 inf 7
6 | inf 0 1 0 inf 1 inf
8 | 0 6 inf 8 inf 0 inf
2 3 4 5 6 7
__________________________________________
1 | inf 0 0 inf inf inf
3 | 0 inf 0 0 0 inf
4 | inf 0 inf 5 1 1
5 | inf 0 5 inf 0 inf
6 | inf 0 1 0 inf 0
8 | inf 0 inf 2 inf inf
3 4 5 6 7
____________________________________
1 | inf 0 inf inf inf
4 | 0 inf 5 1 1
5 | 0 5 inf 0 inf
6 | 0 1 0 inf 0
8 | inf inf 0 inf inf
3 5 6 7
______________________________
4 | inf 4 0 inf
5 | 0 inf 0 inf
6 | 0 0 inf 0
8 | inf 0 inf inf
Maxs — 4 5 5 3 5 6 8 5
3 5 6
________________________
4 | inf 0 inf
5 | 0 inf 0
8 | inf 0 inf
3 6
__________________
5 | 0 0
8 | inf inf
5 6
__________________
4 | 0 inf
8 | 0 inf
3 5
__________________
4 | inf 0
8 | inf 0
3 6
__________________
4 | inf inf
5 | 0 0
Bad road
Maxs — 4 6 5 6 6 3 6 7
3 6 7
________________________
4 | inf 0 inf
5 | inf 0 inf
6 | 0 inf 0
3 7
__________________
5 | inf inf
6 | 0 0
3 7
__________________
4 | inf inf
6 | 0 0
6 7
__________________
4 | 0 inf
5 | 0 inf
3 6
__________________
4 | inf 0
5 | inf 0
Bad road
Maxs — 1 4
3 4 6 7
______________________________
1 | inf 0 inf inf
4 | 0 inf 1 1
5 | inf 5 0 inf
6 | 0 1 inf 0
Maxs — 4 6 5 6 6 3 6 7
3 6 7
________________________
4 | inf 0 inf
5 | inf 0 inf
6 | 0 inf 0
3 7
__________________
5 | inf inf
6 | 0 0
3 7
__________________
4 | inf inf
6 | 0 0
6 7
__________________
4 | 0 inf
5 | 0 inf
3 6
__________________
4 | inf 0
5 | inf 0
Естественно полный вывод решения и вывод всех ветвей можно выключить. Возможно, я сделал много лишней работы, но надеюсь моя статья чем-нибудь вам поможет.
- Занимательные задачки
- C++
- Алгоритмы
Источник: habr.com
Решаем задачу коммивояжёра простым перебором
Вчера мы рассказывали, что такое задача коммивояжёра. Если коротко — это класс задач на поиск кратчайшего маршрута среди нескольких городов. Или маршрута по городу. Или поиск оптимальной квартиры для аренды по нескольким параметрам. В общем — это задачи о том, как принимать решения в ситуациях со множеством переменных.
Сегодня мы попробуем решить классическую задачу коммивояжёра самым простым способом — простым полным перебором.
Мы знаем, что решить задачу коммивояжёра полным перебором не получится, если у нас много городов. Но мы попробуем и посмотрим, какой получится код и как его можно оптимизировать.
Города и расстояния
Допустим, у нас есть 5 городов, каждый из которых соединён с другим:

Из-за рельефа местности близкие города не всегда соединены по прямой, но для простоты мы нарисовали так. Теперь проставим время, которое требуется для переезда из города в город:

Чтобы было удобно пользоваться расстояниями, сделаем табличку:
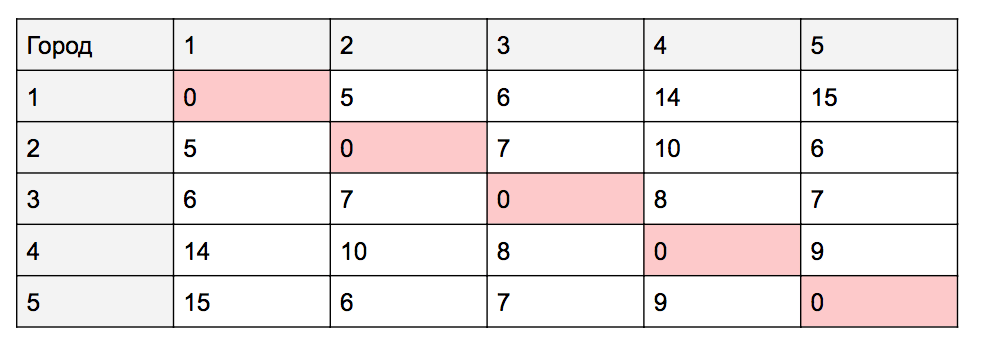
Нулевые ячейки означают, что здесь нет маршрута, потому что это путь из одного и того же города и обратно. Остальные числа — это расстояния между городами. Например, расстояние между первым и третьим городом — 6 километров, а между четвёртым и вторым — 10 километров.
На языке JavaScript это будет выглядеть так:
// таблица с расстояниями между городами var towns = [ [0, 5, 6, 14, 15], [5, 0, 7, 10, 6], [6, 7, 0, 8, 7], [14, 10, 8, 0, 9], [15, 6, 7, 9, 0] ];
Логика работы
Наша задача — найти такой маршрут, в котором сумма километров будет минимальной.
Скрипт полного перебора будет работать так:
- С помощью 5 вложенных циклов мы сможем перебрать все варианты маршрутов.
- В каждом цикле проходим от 0 до 4, потому что у нас 5 городов. Если бы у нас было 10 городов, нам нужно было бы сделать 10 вложенных циклов и в каждом цикле проходить от 0 до 9, чтобы перебрать все возможные расстояния для этого города.
- На каждом шаге проверяем, чтобы у нас не повторялись города в маршруте, потому что в каждом можно побывать только один раз.
- Если это условие выполняется, то запоминаем очередной маршрут и считаем его длину.
- Если длина получилась меньше, чем наименьшая до этого — значит, сейчас у нас получился самый короткий маршрут. Возможно, на следующих шагах цикла мы найдём маршрут ещё короче, но пока минимальный — этот. Делаем эту длину наименьшей и запоминаем номер маршрута.
- Так прогоняем все комбинации городов.
- Выводим найденный минимальный маршрут и его длину.
Скрипт
Для работы скрипта нам понадобятся такие переменные:
- Массив, где мы будем хранить все просчитанные маршруты.
- Порядковый номер текущего маршрута. Как только обрабатываем очередной маршрут, будем увеличивать номер на единицу, чтобы сохранить новый маршрут под новым номером.
- Переменная, где хранится самый короткий путь. Чтобы уже на первом шаге у нас было с чем сравнивать длину маршрута, поместим в неё заведомо большое число, например, 10 000 километров. Как только мы найдём путь короче (а мы найдём), заменим его новым минимальным расстоянием.
- Номер самого короткого маршрута. С его помощью мы вытащим из массива со всеми маршрутами самый короткий из них.
Соберём скрипт. Читайте комментарии:
// таблица с расстояниями между городами var towns = [ [0, 5, 6, 14, 15], [5, 0, 7, 10, 6], [6, 7, 0, 8, 7], [14, 10, 8, 0, 9], [15, 6, 7, 9, 0] ]; // массив, где будут храниться все просчитанные маршруты var path =[]; // порядковый номер текущего маршрута var counter = 0; // самый короткий путь — сразу ставим заведомо большим, чтобы уменьшать его по мере работы алгоритма var minPath = 10000; // номер самого короткого маршрута var minCounter; // перебираем все варианты перемещения по городам for (var i1 = 0; i1 // когда всё сделали, увеличиваем номер маршрута counter +=1; > > > > > >; // когда прошли все варианты, выводим найденное решение console.log(‘Путь с самой короткой длиной маршрута: ‘ + path[minCounter] + ‘(‘ + minPath + ‘ км.)’);
Разбираем результат
Когда мы запустим скрипт в консоли браузера, то увидим такое:

Скрипт на каждом шаге выводил текущий маршрут, который он проверял, а в конце выдал результат. Если мы пролистаем наверх весь вывод маршрутов, то увидим, как скрипт постепенно находил маршруты всё короче и короче:

Но только ближе к концу он нашёл самый короткий путь, который и вошёл в итоговый результат:
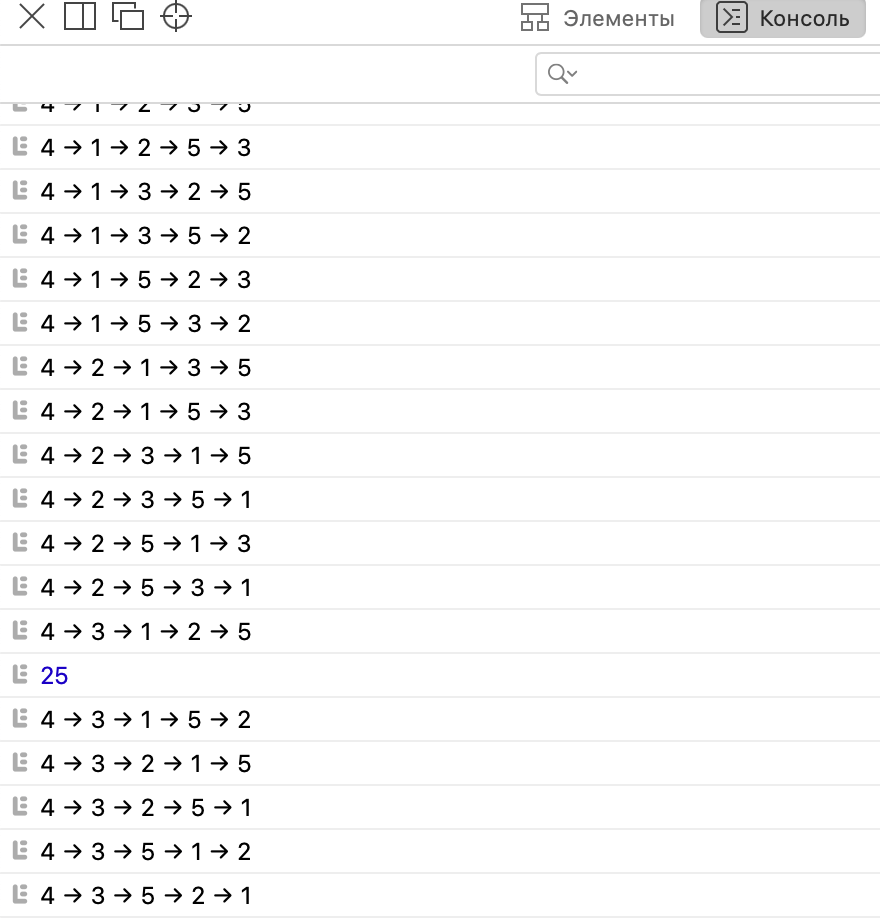
Что здесь не так
С одной стороны, у нас получился простой и понятный алгоритм, который делает то, что нам нужно. С другой — у него есть серьёзные проблемы:
- Если у нас будет 15 городов, нам нужно будет делать 15 вложенных циклов и делать 120 проверок — это выглядит очень громоздко, легко ошибиться в таком коде.
- Чем больше будет городов, тем медленнее будет считаться результат. Уже на 10 городах мы получим 3,5 миллиона выполнений тела цикла, что займёт гораздо больше времени. На 13 городах таких выполнений будет уже 6 миллиардов, и компьютер может их считать неделю или даже больше.
Попробуем исправить эти недостатки в следующих подходах к задаче. Следите за новыми статьями.
Источник: thecode.media