Калькулятор использует метод наименьших квадратов для аппроксимации функции одной переменной. В случае ввода дополнительных условий используется метод множителей Лагранжа.
Эта страница существует благодаря следующим персонам
Timur
- Статья : Аппроксимация функции одной переменной методом наименьших квадратов с дополнительными условиями — Автор
- Калькулятор : Аппроксимация функции одной переменной методом наименьших квадратов с дополнительными условиями — Автор
Создан: 2020-06-03 09:35:19 , Последнее изменение: 2021-01-18 15:44:42
Найти уравнение функции по точкам онлайн
Калькулятор использует методы регрессии для аппроксимации функции одной переменной.
Интерполяция данных: соединяем точки так, чтобы было красиво
Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии.
Как построить график функции без таблицы
Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:
Немного матчасти

Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек P1nbspPn, называется интерполяцией. Есть множество способов интерполяции, но все они могут быть сведены к тому, что надо найти nnbsp1 функцию для расчёта промежуточных точек на соответствующих сегментах. При этом заданные точки обязательно должны быть вычислимы через соответствующие функции. На основе этого и может быть построен график:
Функции fi могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками Pi) называется сплайном.
В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.
Ставим опыты
Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
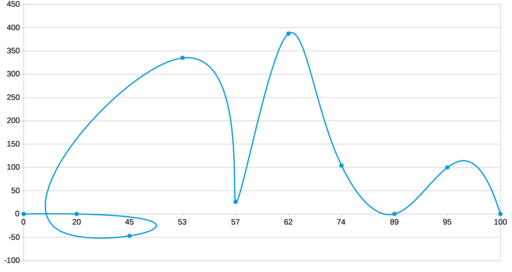
Давайте добавим немного конкретики. Вот набор точек (взяты почти с потолка):
0 0 20 0 45 -47 53 335 57 26 62 387 74 104 89 0 95 100 100 0
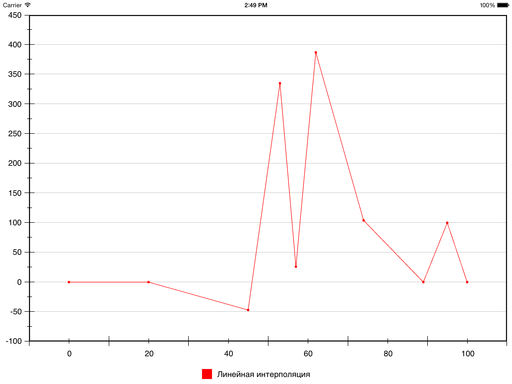
Результат линейной интерполяции этих точек выглядит так:
Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnline
Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.
Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a;nbsp–nbsp+nbsp–nbsp=nbsp–nbsp=nbsp–nbsp–nbsp–nbsp+nbsp=nbsp=nbspyi) и Pinbsp1(xinbsp1,nbsp+nbsp+nbsp–https://habr.com/ru/articles/264191/» target=»_blank»]habr.com[/mask_link]