Программа для решения задачи коммивояжера

При обсуждении метода «грубой силы» (последовательный перебор) была сформулирована задача коммивояжёра:

Eсть N городов, соединённых между собой дорогами. Необходимо проложить между ними кратчайший замкнутый маршрут, проходящий через каждый город только один раз.

Расстояние из города j в город i считается неотрицательным числом: Dji ≥ 0. Это не обязательно «физическая длина» дороги. «Расстоянием» может быть время перемещения, стоимость билета или произвольное неотрицательное число. Часто Dji называют стоимостью ребра (edge costs), так как дороги можно представить рёбрами (edges), соединяющими города-вершины (vertices) некоторого графа.

• Симметричная проблема коммивояжёра (TSP = traveling salesman problem) в которой расстояния заданы между любыми двумя городами и матрица расстояний симметрична: Dji = Dij.
• Асимметричная проблема коммивояжёра (ATSP) допускает несимметричность матрицы Dji ≠ Dij. В ещё более общем случае, пути между некоторыми городами могут отсутствать (== иметь бесконечную длину).
• Задача с частичным упорядочиванием (SOP = sequential ordering problem) требующая, чтобы определённый город i был посещён до города j (таких условий может быть несколько).
• Поиск цикла Гамильтона (HCP = нamiltonian cycle problem) — обнаружение в произвольном графе замкнутых путей, проходящих через каждую вершину в точности один раз.

Евклидова задача коммивояжёра

Если Dji = Dij и расстояния между любыми городами i, j, k удовлетворяют неравенству треугольника: Dij + Djk ≥ Dik, то задачу коммивояжёра называют метрической. Её частным случаем является задача соединения кратчайшей замкнутой ломаной линией точек на плоскости (расстояние равно обычному евклидовому расстоянию).

Решение задачи коммивояжера с помощью библиотеки python-tsp

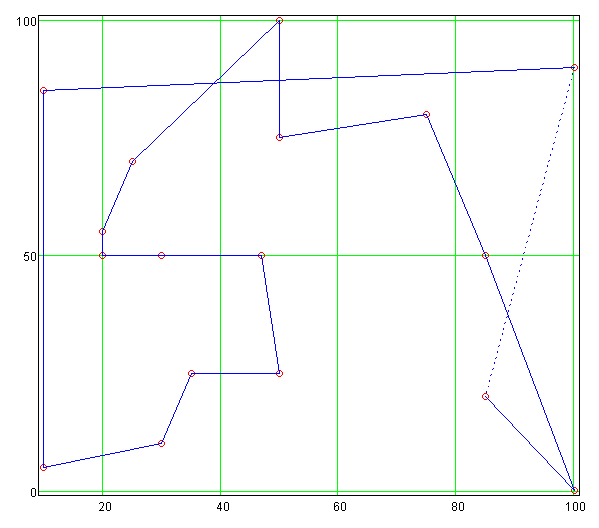
Ниже приведены решения такой задачи для 20 и 50 городов: Несложно видеть, что в евклидовой задача коммивояжёра (ETSP) оптимальный путь не должен иметь пересечений. Действительно, пусть есть некоторый путь, изображённый ниже на первом рисунке. Пунктиром обозначены остальные его участки (т.е. приведены только 4-е города).

Если перебросить два участка пути (как на второй картинке), то общий путь вырастет (сумма диагоналей 4-угольника всегда длиннее суммы двух противоположных сторон): С ETSP связаны интересные вопросы статистического характера. Рассмотрим, например, квадрат в котором случайно, с равномерным распределением размещено N городов. Оказывается, что в большинстве случаев такие «карты городов» имеют кратчайшие пути примерно одной длины, пропорциональной квадратному корню из N.

Методы решения

• Полный перебор перестановок N-1 чисел (стартовый город фиксирован). Практически бесполезен при N > 15.
• Направленный поиск с возвратами — перебор вариантов «вокруг» некоторого решения с отсечением путей, имеющих длину большую, чем лучший к текущему моменту путь.
• Метод ветвей и границ — наиболее эффективный из известных метод отсечения «неперспективных» узлов, за счёт анализа матрицы расстояний. При поиске оптимального решения строится бинарное дерево (в каждом узле порождаются 2 ветви: коммивояжёр идёт в некоторый город или не идёт в него).
• Линейное программирование применяется для минимизации (с ограничениями) линейной формы d·x, где x — искомый бинарный вектор размерности N(N-1)/2, компоненты которого xi равны 1 или 0, в зависимости от того, входит i-е ребро в путь или нет. Вектор d (той же размерности) равен длинам рёбер.

• Жадный алгоритм при выборе очередного города берёт ближайший не посещённый до этого город.
• Метод шнурка — геометрическая вариация жадного алгоритма, в которой города охватываются замкнутым контуром. Он постепенно растягивается, стараясь пройти через все города, минимальным образов увеличив свою длину.
• Скользящий перебор переставляет местами города из небольшой части пути. Затем такое «окно перебора» скользит вдоль всего пути. Метод имеет различные вариации и оказывается эффективным способом улучшения решения, найденного предыдущими двумя эвристическими методами.

• Метод отжига в котором происходят перестановки городов с постепенно «затухающей» интенсивностью. При этом постоянно сохраняется наилучшее найденное решение.
• Генетический алгоритм — более «продвинутый» вариант, при котором создаётся большое количество различных путей. Они постоянно «мутируют» и «скрещиваются» друг с другом, обмениваясь отдельным участками.

Немного истории

Полезные ресурсы

• TSPLib — проект, развивающийся с 1990-х. Содержит карты с массивами координат реальных городов и оптимальный TSP-путь. Является отличным источником для тестирования алгоритмов. Современная поддержка проекта находится здесь.
• Книга — «The Traveling Salesman Problem: A Computational Study», D.L. Applegate, R.E. Bixby, V. Chvátal https://synset.com/ai/ru/tsp/Salesman_Intro.html» target=»_blank»]synset.com[/mask_link]

  Решение задачи коммивояжера. Метод ветвей и границ.

  Программные продукты и системы

  (сведения по итогам 2021 г.)
  2-летний импакт-фактор РИНЦ: 0,441
  2-летний импакт-фактор РИНЦ без самоцитирования: 0,408
  Двухлетний импакт-фактор РИНЦ с учетом цитирования из всех
  источников: 0,704
  5-летний импакт-фактор РИНЦ: 0,417
  5-летний импакт-фактор РИНЦ без самоцитирования: 0,382
  Суммарное число цитирований журнала в РИНЦ: 9837
  Пятилетний индекс Херфиндаля по цитирующим журналам: 149
  Индекс Херфиндаля по организациям авторов: 384
  Десятилетний индекс Хирша: 71
  Место в общем рейтинге SCIENCE INDEX за 2021 год: 196
  Место в рейтинге SCIENCE INDEX за 2021 год по тематике «Автоматика. Вычислительная техника»: 4
  Место в рейтинге SCIENCE INDEX за 2021 год по тематике «Кибернетика» 2

  Источник: www.swsys.ru

  Решение задачи коммивояжёра методом ближайшего соседа на Python

  

  2017-05-27 в 14:52, admin , рубрики: python, задача коммивояжёра, метод ближайшего соседа

  Быстрый и простой алгоритм требующий модификации

  Среди методов решения задачи коммивояжёра метод ближайшего соседа привлекает простотой алгоритма. Метод ближайшего соседа в исходной формулировке заключается в нахождении замкнутой кривой минимальной длины, соединяющей заданный набор точек на плоскости [1]. Моё внимание привлекла наиболее распространённая реализация данного алгоритма в пакете Mathcad, размещённая в сети на ресурсе [2]. Сама реализация не совсем удобна, например, нельзя вывести матрицу расстояний между пунктами или проанализировать альтернативные маршруты.

  На ресурсе [2] приведена следующая вполне справедливая критика данного метода. «Маршрут не оптимальный (не самый короткий) и сильно зависит от выбора первого города. Фактически не решена задача коммивояжера, а найдена одна гамильтонова цепь графа».

  Там же предложен путь некоторого усовершенствования метода ближайшего соседа. «Следующий возможный шаг оптимизации — «развязывание петель» (ликвидация перекрестий). Другое решение — перебор всех городов (вершин графа) в качестве начала маршрута и выбор наикратчайшего из всех маршрутов». Однако реализация последнего предложения не приведена. Учитывая все перечисленные обстоятельства, я решил реализовать приведенный алгоритм на Python и при этом предусмотреть возможность выбора начального пункта по критерию минимальной длины марщрута.

  Код программы с генерацией случайных значений координат пунктов

  #!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import numpy as np from numpy import exp,sqrt n=50;m=100;ib=3;way=[];a=0 X=np.random.uniform(a,m,n) Y=np.random.uniform(a,m,n) #X=[10, 10, 100,100 ,30, 20, 20, 50, 50, 85, 85, 75, 35, 25, 30, 47, 50] #Y=[5, 85, 0,90,50, 55,50,75 ,25,50,20,80,25,70,10,50,100] #n=len(X) M = np.zeros([n,n]) # Шаблон матрицы относительных расстояний между пунктами for i in np.arange(0,n,1): for j in np.arange(0,n,1): if i!=j: M[i,j]=sqrt((X[i]-X[j])**2+(Y[i]-Y[j])**2)# Заполнение матрицы else: M[i,j]=float(‘inf’)#Заполнение главной диагонали матрицы way.append(ib) for i in np.arange(1,n,1): s=[] for j in np.arange(0,n,1): s.append(M[way[i-1],j]) way.append(s.index(min(s)))# Индексы пунктов ближайших городов соседей for j in np.arange(0,i,1): M[way[i],way[j]]=float(‘inf’) M[way[i],way[j]]=float(‘inf’) S=sum([sqrt((X[way[i]]-X[way[i+1]])**2+(Y[way[i]]-Y[way[i+1]])**2) for i in np.arange(0,n-1,1)])+ sqrt((X[way[n-1]]-X[way[0]])**2+(Y[way[n-1]]-Y[way[0]])**2) plt.title(‘Общий путь-%s.Номер города-%i.Всего городов -%i.n Координаты X,Y случайные числа от %i до %i’%(round(S,3),ib,n,a,m), size=14) X1=[X[way[i]] for i in np.arange(0,n,1)] Y1=[Y[way[i]] for i in np.arange(0,n,1)] plt.plot(X1, Y1, color=’r’, linestyle=’ ‘, marker=’o’) plt.plot(X1, Y1, color=’b’, linewidth=1) X2=[X[way[n-1]],X[way[0]]] Y2=[Y[way[n-1]],Y[way[0]]] plt.plot(X2, Y2, color=’g’, linewidth=2, linestyle=’-‘, label=’Путь от последнего n к первому городу’) plt.legend(loc=’best’) plt.grid(True) plt.show()

  В результате работы программы получим.

  

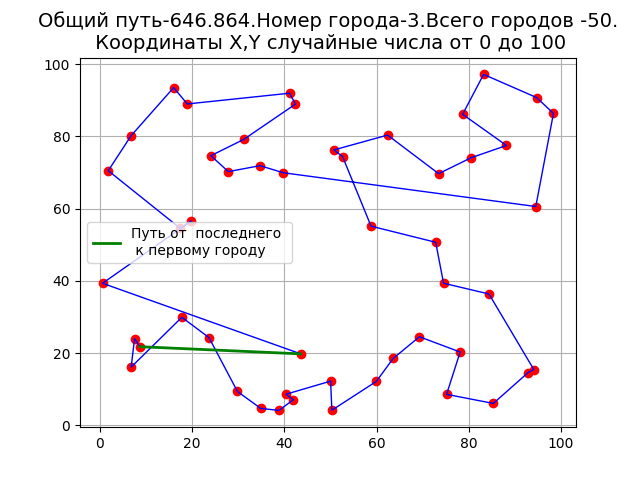
  Недостатки метода видны на графике, о чём свидетельствуют петли. Реализации алгоритма на Python имеет больше возможностей, чем в Mathcad. Например, можно вывести матрицу расстояний между пунктами на печать. Например, для n=4, получим:

  [[ inf 43.91676312 48.07577298 22.15545245] [43.91676312 inf 54.31419355 21.7749088 ] [48.07577298 54.31419355 inf 46.92141965] [ 22.15545245 21.7749088 46.92141965 inf]]

  Для работы алгоритма на главной диагонали матрицы числовые значения устанавливают равными бесконечности.

  От случайных координат пунктов перейдем к заданным. Данные возьмём на ресурсе [2]. Для работы программы в режиме заданных координат в приведенном листинге уберём комментарии со следующих строк.

  X=[10, 10, 100,100 ,30, 20, 20, 50, 50, 85, 85, 75, 35, 25, 30, 47, 50] Y=[5, 85, 0,90,50, 55,50,75 ,25,50,20,80,25,70,10,50,100] n=len(X)

  В результате роботы программы получим.

  

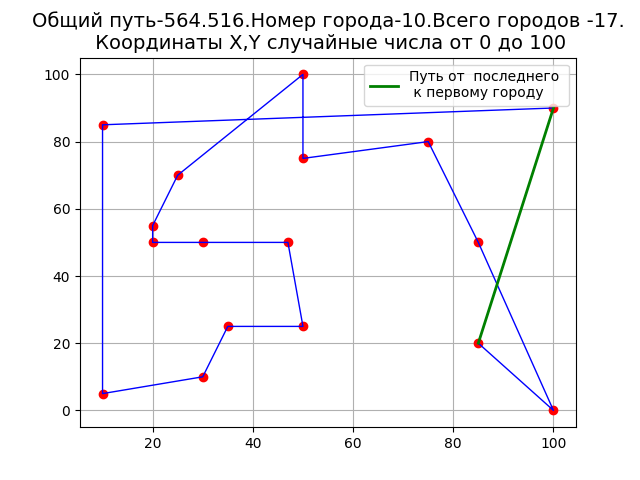
  Из приведенного графика видно, что траектории перемещения коммивояжёра пересекаться.

  Сравнение реализаций алгоритма

  Для сравнения результатов работы моей программы с программой на ресурсе [2], установим на ресурсе те же параметры, с той лишь разницей, что у меня нумерация пунктов(городов) начинается с 0, а на ресурсе с 1. Тогда номер города на ресурсе n=11, получим:

  

  Длина маршрута 564, 516 и расположение пунктов полностью совпадают.

  Усовершенствование алгоритма ближайшего соседа

  Теперь можно модифицировать мою программу по критерию минимальной длины маршрута.

  Код программы для определения начального пункта из условия минимальной длины маррута(модифицированный алгоритм).

  #!/usr/bin/env python #codi import matplotlib.pyplot as plt import numpy as np from numpy import exp,sqrt n=50;m=100;way=[];a=0 X=np.random.uniform(a,m,n) Y=np.random.uniform(a,m,n) X=[10, 10, 100,100 ,30, 20, 20, 50, 50, 85, 85, 75, 35, 25, 30, 47, 50] Y=[5, 85, 0,90,50, 55,50,75 ,25,50,20,80,25,70,10,50,100] n=len(X) RS=[];RW=[];RIB=[] s=[] for ib in np.arange(0,n,1): M = np.zeros([n,n]) for i in np.arange(0,n,1): for j in np.arange(0,n,1): if i!=j: M[i,j]=sqrt((X[i]-X[j])**2+(Y[i]-Y[j])**2) else: M[i,j]=float(‘inf’) way=[] way.append(ib) for i in np.arange(1,n,1): s=[] for j in np.arange(0,n,1): s.append(M[way[i-1],j]) way.append(s.index(min(s))) for j in np.arange(0,i,1): M[way[i],way[j]]=float(‘inf’) M[way[i],way[j]]=float(‘inf’) S=sum([sqrt((X[way[i]]-X[way[i+1]])**2+(Y[way[i]]-Y[way[i+1]])**2) for i in np.arange(0,n-1,1)])+ sqrt((X[way[n-1]]-X[way[0]])**2+(Y[way[n-1]]-Y[way[0]])**2) RS.append(S) RW.append(way) RIB.append(ib) S=min(RS) way=RW[RS.index(min(RS))] ib=RIB[RS.index(min(RS))] X1=[X[way[i]] for i in np.arange(0,n,1)] Y1=[Y[way[i]] for i in np.arange(0,n,1)] plt.title(‘Общий путь-%s.Номер города-%i.Всего городов -%i.n Координаты X,Y заданы’%(round(S,3),ib,n), size=14) plt.plot(X1, Y1, color=’r’, linestyle=’ ‘, marker=’o’) plt.plot(X1, Y1, color=’b’, linewidth=1) X2=[X[way[n-1]],X[way[0]]] Y2=[Y[way[n-1]],Y[way[0]]] plt.plot(X2, Y2, color=’g’, linewidth=2, linestyle=’-‘, label=’Путь от последнего n к первому городу’) plt.legend(loc=’best’) plt.grid(True) plt.show() Z=sqrt((X[way[n-1]]-X[way[0]])**2+(Y[way[n-1]]-Y[way[0]])**2) Y3=[sqrt((X[way[i+1]]-X[way[i]])**2+(Y[way[i+1]]-Y[way[i]])**2) for i in np.arange(0,n-1,1)] X3=[i for i in np.arange(0,n-1,1)] plt.title(‘Пути от города к городу’) plt.plot(X3, Y3, color=’b’, linestyle=’ ‘, marker=’o’) plt.plot(X3, Y3, color=’r’, linewidth=1, linestyle=’-‘, label=’Без учёта замыкающего пути — %s’%str(round(Z,3))) plt.legend(loc=’best’) plt.grid(True) plt.show ()

  Результат работы программы.

  

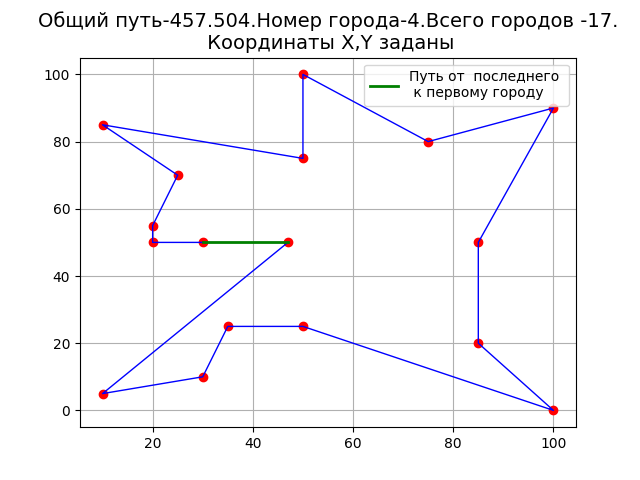
  Петель на графике нет, что свидетельствует об улучшении алгоритма.

  

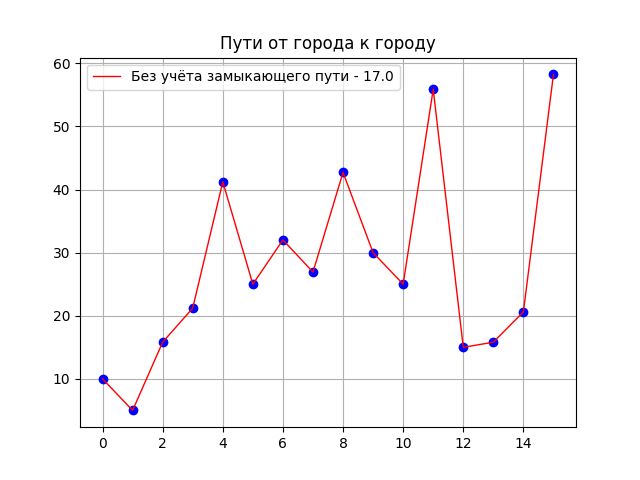
  Длина маршрута при начале движения из пункта с номером 4 меньше, чем при начале движения из других пунктов.

  Длина маршрута — 458.662, при начале движения из пункта — 0 Длина маршрута — 463.194, при начале движения из пункта — 1 Длина маршрута — 560.726, при начале движения из пункта — 2 Длина маршрута — 567.48, при начале движения из пункта — 3 Длина маршрута — 457.504, при начале движения из пункта — 4 Длина маршрута — 465.714, при начале движения из пункта — 5 Длина маршрута — 471.672, при начале движения из пункта — 6 Длина маршрута — 460.445, при начале движения из пункта — 7 Длина маршрута — 533.461, при начале движения из пункта — 8 Длина маршрута — 532.326, при начале движения из пункта — 9 Длина маршрута- 564.516, при начале движения из пункта — 10 Длина маршрута — 565.702, при начале движения из пункта — 11 Длина маршрута — 535.539, при начале движения из пункта — 12 Длина маршрута — 463.194, при начале движения из пункта — 13 Длина маршрута — 458.662, при начале движения из пункта — 14 Длина маршрута — 457.504, при начале движения из пункта — 15 Длина маршрута- 508.045, при начале движения из пункта — 16

  Зависимость длины маршрута от количества пунктов(городов)

  Для этого вернёмся к генерации случайных значений координат. По результатам работы программы увеличивая количество пунктов до 1000 с шагов в 100 составим таблицу из двух строк, в одной длины маршрутов в другой количество пунктов в маршруте.

  

  Аппроксимируем приведенные данные с помощью программы.

  #!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt def mnkLIN(x,y): a=round((len(x)*sum([x[i]*y[i] for i in range(0,len(x))])-sum(x)*sum(y))/(len(x)*sum([x[i]**2 for i in range(0,len(x))])-sum(x)**2),3) b=round((sum(y)-a*sum(x))/len(x) ,3) y1=[round(a*w+b ,3) for w in x] s=[round((y1[i]-y[i])**2,3) for i in range(0,len(x))] sko=round((sum(s)/(len(x)-1))**0.5,3) p=(sko*len(x)*100)/sum(y1) plt.title(‘Аппроксимация методом наименьших n квадратов Y=%s*x+%s с погрешностью -%i -проц.’%(str(a),str(b),int(p)), size=14) plt.xlabel(‘Количество городов’, size=14) plt.ylabel(‘Длина маршрутов’, size=14) plt.plot(x, y, color=’r’, linestyle=’ ‘, marker=’o’, label=’Данные метода ближайшего соседа’) plt.plot(x, y1, color=’b’,linewidth=1, label=’Аппроксимирующая прямая’) plt.legend(loc=’best’) plt.grid(True) plt.show() y=[933.516, 1282.842, 1590.256, 1767.327 ,1949.975, 2212.668, 2433.955, 2491.954, 2549.579, 2748.672] x=[100,200,300,400,500,600, 700,800, 900,1000] mnkLIN(x,y)

  

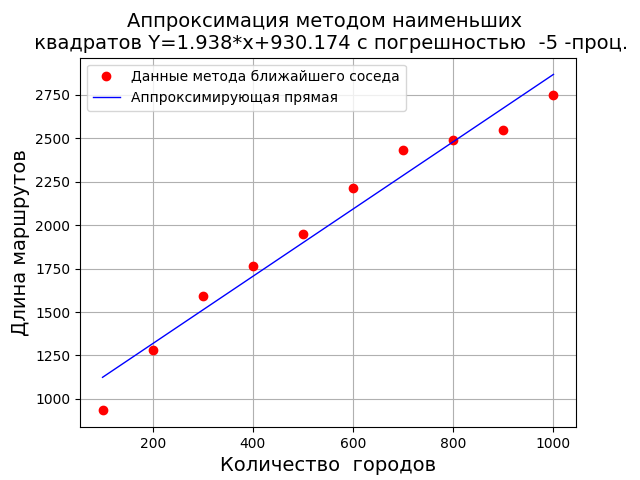
  При использовании метода ближайшего соседа длина маршрута и число пунктов связаны линейной зависимостью в приведенном диапазоне. В работе [3] проведен анализ основных методов решения задачи коммивояжёра. По приведенным данным лучшие результаты показали алгоритм Литтла, генетический алгоритм и модификация алгоритма «иди в ближний». Что является дополнительным основанием для проведенного в данной статье анализа решения задачи коммивояжёра методом ближайшего соседа.

  Выводы

  Известно, что Python свободно распространяемый язык программирования. Реализации метода ближайшего соседа на Python в доступных мне источниках я не нашёл. Предложенная мною простая реализация метода безусловно далека от совершенства, но позволяет анализировать все этапы метода — создания матрицы расстояний между пунктами, поиск короткого маршрута, модификацию алгоритма, особенности графического отображения результатов поиска маршрута. Всё это важные факторы особенно в процессе обучения, когда специальные математические пакеты в силу понятных причин не доступны. Поэтому надеюсь, что мои тщедушные попытки обойтись без дорогостоящих математических пакетов хотя бы для отдельных задач будут способствовать не только рациональной организации обучения, но и популяризации языка программирования Python.

  Спасибо всем, кто прочитает статью и, может быть, найдёт применение полученным результатам.

  Ссылки

  1. Алгоритм ближайшего соседа в задаче коммивояжёра.
  2. Решение задачи коммивояжера методом ближайшего соседа.
  3. Сравнительный анализ методов решения задачи коммивояжера для выбора маршрута прокладки кабеля сети кольцевой архитектуры.

  Источник: www.pvsm.ru