This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
Switch branches/tags
Branches Tags
Could not load branches
Nothing to show
Could not load tags
Nothing to show
Name already in use
A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?
Cancel Create
- Local
- Codespaces
HTTPS GitHub CLI
Use Git or checkout with SVN using the web URL.
Work fast with our official CLI. Learn more about the CLI.
Sign In Required
Please sign in to use Codespaces.
Launching GitHub Desktop
If nothing happens, download GitHub Desktop and try again.
Launching GitHub Desktop
If nothing happens, download GitHub Desktop and try again.
Launching Xcode
If nothing happens, download Xcode and try again.
Прямая геодезическая задача. Формулировка. Определение
Launching Visual Studio Code
Your codespace will open once ready.
There was a problem preparing your codespace, please try again.
Latest commit
Git stats
Files
Failed to load latest commit information.
Latest commit message
Commit time
README.md
Библиотека предназначена для решения геометрических задач на выгнутой поверхности сфероида или эллипсоида вращения.
С помощью библиотеки можно:
- решить прямую геодезическую задачу;
- решить обратную геодезическую задачу;
- найти точку пересечения двух ортодромий, заданных кординатами концов;
- зная координаты концов ортодромии, найти значение широты по известной долготе;
- зная координаты концов ортодромии, найти значение долготы по известной широте;
Прямой геодезической задачей называют вычисление геодезических координат — широты и долготы точки, лежащей эллипсоиде, по координатам другой точки и по известным длине и дирекционному углу направления, соединяющей эти точки.
Обратная геодезическая задача заключается в определении по геодезическим координатам двух точек на эллипсоиде длины и дирекционного угла направления между этими точками.
Ортодромия — название кратчайшего расстояния между двумя точками на поверхности Земли или другого эллипсоида вращения.
Решение прямой геодезической задачи
Для решения прямой геодезической задачи, неоходимо создать объект класса DirectProblemService .
var directEllipsoid = new DirectProblemService(new Ellipsoid()); var directSpheroid = new DirectProblemService(new Spheroid());
В качестве параметра в конструктор следует передать объект реализующий интерфейс IEllipsoid , в котором задаются полярный и экваториальный радиус, а так же коэффициент полярного сжатия.
Для решения прямой задачи вызвать метод DirectProblem , в который передать в качестве параметров, начальную точку, азимут = направление и расстояние:
Решение прямой геодезической задачи
var point1 = new Point(15, 25, 53, CardinalLongitude.W, 28, 7, 38, CardinalLatitude.N); var azimuth = 21; var distance = 2000; var directAnswer = directEllipsoid.DirectProblem(point1, azimuth, distance);
Ответ directAnswer содержит вторую точку ортодромии Сoordinate и обратный азимут ReverseAzimuth .
Решение обратной геодезической задачи
Для решения обратной геодезической задачи, неоходимо создать объект класса InverseProblemService .
var inverseEllipsoid = new InverseProblemService(new Ellipsoid()); var inverseSpheroid = new InverseProblemService(new Spheroid());
В качестве параметра в конструктор следует передать объект реализующий интерфейс IEllipsoid , в котором задаются полярный и экваториальный радиус, а так же коэффициент полярного сжатия.
Для решения обратной задачи вызвать метод OrthodromicDistance , в который передать в качестве параметров, две точки:
var point1 = new Point(15, 25, 53, CardinalLongitude.W, 28, 7, 38, CardinalLatitude.N); var point2 = new Point(59, 36, 30, CardinalLongitude.W, 13, 5, 46, CardinalLatitude.N); var inverseAnswer = inverseEllipsoid.OrthodromicDistance(point1, point2);
Ответ inverseAnswer содержит прямой и обратный азимуты ForwardAzimuth , ReverseAzimuth , а также расстояние между точками Distance .
Вычисление точки пересечения ортодромий
Для вычисления точки пересечения ортодромий, неоходимо создать объект класса IntersectService .
var intersectEllipsoid = new IntersectService(new Ellipsoid()); var intersectSpheroid = new IntersectService(new Spheroid());
В качестве параметра в конструктор следует передать объект реализующий интерфейс IEllipsoid , в котором задаются полярный и экваториальный радиус, а так же коэффициент полярного сжатия.
Для рассчёта вызвать метод IntersectOrthodromic , в который передать в качестве параметров, по две точки для каждой из двух ортодромий:
var point1 = new Point(22, 36, 30, CardinalLongitude.E, 13, 5, 46, CardinalLatitude.N); var point2 = new Point(27, 25, 53, CardinalLongitude.E, 15, 7, 38, CardinalLatitude.N); var point3 = new Point(20, 36, 30, CardinalLongitude.E, 17, 5, 46, CardinalLatitude.N); var point4 = new Point(26, 25, 53, CardinalLongitude.E, 13, 7, 38, CardinalLatitude.N); var intersectCoord = intersectEllipsoid.IntersectOrthodromic(point1, point2, point3, point4);
Ответом будет точка — объект класса Point , в котором определены долгота и широта, в десятичных градуса ( Longitude , Latitude ) или в радианах ( LonR , LatR ).
Вычисление широты по долготе или долготы по широте
Для рассчётов, неоходимо создать объект класса IntermediatePointService .
var intermediateEllipsoid = new IntermediatePointService(new Ellipsoid()); var ntermediateSpheroid = new IntermediatePointService(new Spheroid());
В качестве параметра в конструктор следует передать объект реализующий интерфейс IEllipsoid , в котором задаются полярный и экваториальный радиус, а так же коэффициент полярного сжатия.
Для вычисления широты вызвать метод GetLatitude , в который передать значение долготы, для которого мы вычисляем широту, и две координаты характеризующие ортодромию.
var coord1 = new Point(10, 10); var coord2 = new Point(30, 50); var lat = intermediateEllipsoid.GetLatitude(20, coord1, coord2);
Для вычисления долготы вызвать метод GetLongitude , в который передать значение широты, для которого мы вычисляем долготу, и две координаты характеризующие ортодромию.
var coord1 = new Point(10, 10); var coord2 = new Point(30, 50); var lat = intermediateEllipsoid.GetLongitude(20, coord1, coord2);
В обоих случая ответом будет значение типа double .
Источник: github.com
Программа для решение прямой геодезической задачи
Рассмотрены особенности организации учебного курса по программированию на С++ в Московском университете геодезии и картографии (МИИГАиК). Курс по программированию характеризуется: использованием учебных компьютерных программ с геодезической тематикой, изучением языка С++ и общей геодезии в параллельном режиме, разработкой узкоспециализированных программ для учебных целей.
Обсуждается код учебной программы для студентов картографов и геодезистов, изучающих основы программирования на языке С++. Программа вычисляет плоские прямоугольные координаты трех точек, заданных на листе топографической карты. Для вычисления координат используется прямая геодезическая задача.
Рассчитанные значения координат сравниваются с измеренными координатами, и определяются погрешности Х и Y координат. Программа демонстрирует применение двумерных и одномерных массивов для хранения исходных и рассчитанных величин.
Показано, как, используя оператор вычисления остатка от целочисленного деления, получить цикл с перебором всех элементов массива без повторного перезаписывания данных в массиве. Показано использование тригонометрических функций косинуса и синуса в цикле и их взаимное преобразование на основе счетчика цикла. Программа выводит на экран рассчитанные координаты точек и погрешности определения координат. Разработанная программа иллюстрирует решение прямой геодезической задачи для вычисления плоских прямоугольных координат множества заданных точек на основе применения технологии процедурного программирования.
обучение программированию
учебная С++ программа
прямая геодезическая задача
вычисление прямоугольных координат точек
1. Прата С. Язык программирования С++. Лекции и упражнения. М.: ООО «И.Д. Вильямс», 2014. 1248 с.
2. Иванова Г.С. Основы программирования. М.: Изд-во МГТУ им. Н.Э.
Баумана, 2014. 416 с.
3. Иванова Г.С., Ничушкина Т.Н., Пугачев Е.К. Объектно-ориентированное программирование. М.: Изд-во МГТУ им. Н.Э. Баумана, 2007. 368 с.
4. Либерти Дж., Кейденхед Р. Освой самостоятельно С++ за 24 часа. М.: ООО «И.Д. Вильямс», 2017. 448 с.
5. Дэвис С. С++ для чайников. М.: ООО «И.Д. Вильямс», 2016. 400 с.
6. Заблоцкий В.Р., Василева С.Ж. Многомодульная учебная программа, моделирующая измерение теодолитом расстояний, горизонтальных и вертикальных углов // Известия высших учебных заведений. Геодезия и аэрофотосъемка. 2018. Т. 62. № 6. С. 632–642.
Отметим некоторые особенности организации учебного курса по программированию на С++ в Московском университете геодезии и картографии (МИИГАиК). Обучение студентов программированию с геодезическим уклоном проводится на младших курсах параллельно с курсом общей геодезии.
Поэтому желательно, чтобы компьютерные программы, используемые на занятиях по программированию, соответствовали той последовательности, в которой учебный материал излагается в курсе общей геодезии. Использование программ с решениями геодезических задач, не изученных студентами в базовом курсе геодезии, является малоэффективным.
Кроме того, в процессе обучении программированию изучаемые конструкции языка должны рассматриваться в определенной последовательности. Это неизбежно приводит к тому, что преподаватель ограничен узким набором языковых конструкций, особенно на начальном этапе курса. Как результат, некоторые учебные программы содержат решения, реализованные не самым эффективным способом. Если понятие «оператор цикла» в курсе программирования изучается раньше понятия «функция», то в программах, иллюстрирующих циклы, нежелательно использовать функции, например тригонометрические функции или функции округления. Что не очень удобно и желательно учитывать при разработке учебных программ.
Заметим, что обучение студентов программированию на С++ часто проводится по классическому учебнику С. Прата [1], учебникам Г.С. Ивановой и др. [2, 3], подготовленным в МГТУ им. Н.Э. Баумана, самоучителям Дж. Либерти и С. Дэвиса [4, 5]. Однако в настоящее время отсутствуют учебники по программированию, ориентированные на подготовку картографов и геодезистов.
Нашей основной задачей [6] является разработка учебных программ. Эти программы не следует рассматривать как универсальные, предназначенные для обработки исходных геодезических данных в широком наборе комбинаций и при разных условиях.
Программы для обучения студентов должны лишь иллюстрировать различные конструкции языка С++ на примере решения конкретных геодезических задач, может, даже и частных задач. Приведем пример, поясняющий сказанное. Известно, что прямая угловая засечка реализуется в геодезической практике, как правило, с дополнительным контрольным пунктом или в виде двукратной прямой засечки с уравниванием полученных данных. Однако если реализовать такую универсальную программу, то её код будет существенно превышать 50 строк и, как следствие, программа станет малопонятной и трудноусваиваемой для первоначального изучения. Поэтому учебные программы должны быть в основном небольшими (объемом до 50 строк), в тоже время охватывающими все разделы современного языка С++.
Материалы и методы исследования
Работа выполнена на персональном компьютере под управлением ОС Microsoft Windows 8.1. Для разработки программы использовалась среда программирования с открытым кодом Code:Blocks и компилятор GCC C++. Созданная программа запускается в командной строке, и результат выводит в командную строку.
В данной работе представлена учебная программа для студентов картографов и геодезистов, демонстрирующая использование прямой геодезической задачи при вычислении плоских прямоугольных координат трех точек, заданных на топографической карте. Рассмотрим геодезическую постановку задачи. Пусть даны три точки на топографической карте А(XА,YА), В(XB,YB) и С(XC,YC).
Требуется определить их координаты по карте и вычислить эти же координаты на основе решения прямой геодезической задачи. Также необходимо сравнить вычисленные и измеренные координаты точек.
Графическая часть задачи состоит в непосредственных измерениях на карте с помощью геодезического транспортира трех дирекционных углов направлений αA, αB, αC и трех расстояний d1, d2, d3 между точками с помощью линейки. Вычислительная часть задачи заключается в использовании формул для решения прямой геодезической задачи и вычислении по формулам координат точек. Прямоугольные X и Y координаты некоторой точки P вычисляются по формулам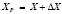 
и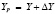 
, где ΔX и ΔY – значения приращения X и Y координат опорной точки, вычисляемые по формулам: 
, 
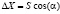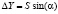и α – дирекционный угол направления. В таблице представлены данные вспомогательных измерений для вычисления координат искомых точек, а также результаты измерения этих же координат по карте. Координаты опорной точки выделены в таблице полужирным шрифтом.
Источник: top-technologies.ru
Tacheometric Survey Processor
Программа «TSP — Tacheometric Survey Processor» — это простая в освоении и удобная в работе программа для камеральной обработки материалов полевых измерений и решения различных геодезических задач. Интерфейс программы оптимизирован на высокую производительность труда и минимизацию операций.
Программа TSP разработана геодезистами. Это значит, что в программе учтены задачи и реальные потребности специалистов в области геодезии. Tacheometric Survey Processor позволяет существенно упростить трудоемкий камеральный процесс обработки полевых измерений: скорость ввода и обработки данных в TSP в несколько раз превышает скорость работы в аналогичных программах, а для освоения функционала программы достаточно всего 2-3 часов.
C 2006 года эта программа успешно используется организациями и частными лицами, занимающимися геодезической деятельностью.
Функционал
Вводить данные в программу TSP можно различными способами:
- вручную, из полевого журнала (программа оптимизирована на скорость ручного ввода до 200-300 измерений в час);
- из файлов, создаваемых пользователем по специальному шаблону в формате UTF (текстовый файл с простой структурой);
- из ранее записанных и сохранённых файлов собственного внутреннего формата *.SRV;
- из файлов, создаваемых геодезическими инструментами (Trimble, 3Ta5, Sokkia).
При работе с данными из файлов геодезических инструментов скорость обработки достигает нескольких тысяч измерений в час.
Обработка и уравнивание введённых данных организованы таким образом, что в программе можно рассчитывать:
- любые типы линейно-угловых ходов (замкнутые, разомкнутые, сомкнутые, висячие, без примычных углов, с правыми и левыми углами) с выводом невязок, приращений и поправок;
- тахеометрию с использованием и без использования результатов уравнивания хода;
- тахеометрию в качестве исходных пунктов стояния и ориентирования;
- дирекционные углы, решения прямой и обратной геодезической задачи, определения недоступной высоты (реализована функция автоматического расчёта этих данных).
Кроме этого, с помощью TSP можно получать координаты 2D (X,Y) и 3D (X,Y,H) в результате уравнивания линейно-углового хода и тахеометрии.
Для оптимизации работы с полученными результатами данные можно сохранять:
Также данные можно сохранять как в текстовые файлы (при сохранении ведомости уравнивания хода и расчета пикетажа), так и в текстовые файлы ASCII (при сохранении ведомостей в формате XYH).
Преимущества
Преимущества «TSP — Tacheometric Survey Processor» — это:
- возможность как автоматического, так и ручного ввода данных и их обработки (в программу встроен модуль скачки данных с любых электронных тахеометров);
- возможность использования сторонних препроцессоров и конвертеров для дальнейшей обработки данных;
- обработка и уравнивание данных с различных инструментов;
- функциональность и удобство в работе;
- интуитивно понятный графический интерфейс;
- малый размер.
Примеры использования
Скриншоты
Совместимость
Tacheometric Survey Processor работает в среде Windows 2000/XP/Vista/7/8 и не требует больших системных ресурсов.
Нужны дополнительные функции?
Функциональность программы TSP постоянно улучшается. Если вы хотите, чтобы в программе появилась новая возможность — пожалуйста, напишите нам об этом.
Источник: www.groundarc.ru