Программа для построения регрессионной модели

Эффективно использовать надстройку Пакет анализа для целей регрессионного анализа могут только пользователи знакомые с теорией регрессионного анализа .

В данной статье решены следующие задачи:

• Показано как в MS EXCEL выполнить регрессионный анализ с помощью надстройки Пакет анализа (инструмент Регрессия), т.е. как вызвать надстройку и правильно заполнить входные данные;
• Даны пояснения по разделам отчета, формированного надстройкой.

В надстройке Пакет анализа для построения линейной регрессионной модели (как простой , так и множественной ) имеется специальный инструмент Регрессия .

После выбора этого инструмента откроется окно, в котором требуется заполнить следующие поля (см. файл примера лист Надстройка ):

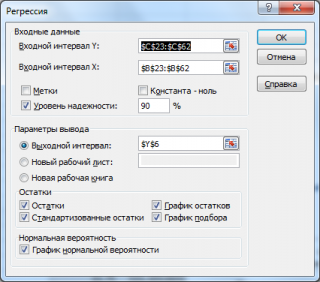
• Входной интервалY : ссылка на массив значений переменной Y. Ссылку можно указать с заголовком. В этом случае, при выводе результатов надстройка использует Ваш заголовок (для этого в окне требуется установить галочку Метки );
• Входной интервал Х : ссылка на значения переменной Х. В случае множественной регрессии (несколько переменных Х) нужно указать все столбцы со значениями Х. В случае множественной регрессии ссылку рекомендуется делать на диапазон с заголовками (в окне требуется установить галочку Метки );
• Константа-ноль : если галочка установлена, то надстройка подбирает линию регрессии, проходящую через точку Y=0 ( сдвиг будет равен 0);
• Уровень надежности : Это значение используется для построения доверительных интервалов для наклона и сдвига . Уровень надежности = 1- альфа. Если галочка не установлена или установлена, но уровень значимости = 95%, то надстройка все равно рассчитывает границы доверительных интервалов, причем дублирует их. Если галочка установлена, а уровень надежности отличен от 95%, то рассчитываются 2 доверительных интервала : один для 95%, другой для введенного значения. Для демонстрации вышесказанного введем 90%;
• Выходной интервал: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона;
• Остатки : будут вычислены остатки модели , т.е. разница между наблюденными и предсказанными значениями Yi для всех наблюдений n;
• Стандартизированные остатки : Вышеуказанные значения остатков будут поделены на значение их стандартного отклонения ;
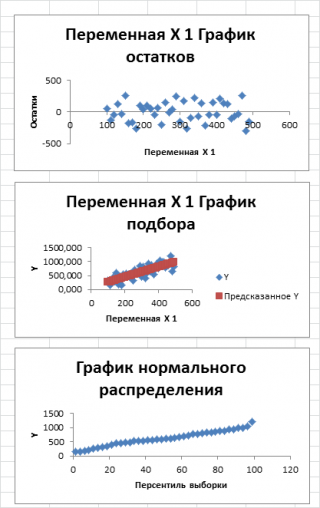
• График остатков : Будет построена точечная диаграмма : значения остатков для всех значений Хi;
• График подбора: Будет построена точечная диаграмма: точки данных (X;Y) и линия регрессии ;
• График нормальной вероятности: Будет построена точечная диаграмма с названием График нормального распределения . По сути — это график значений переменной Y, отсортированных по возрастанию .

В результате вычислений будет заполнен указанный Выходной интервал.

Построение модели множественной регрессии в программе Gretl

Получение регрессионных моделей в Microsoft Excel

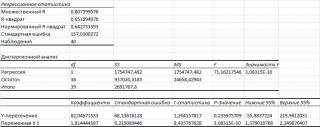
Тот же результат можно получить с помощью формул (см. файл примера лист Надстройка, столбцы I:T ):

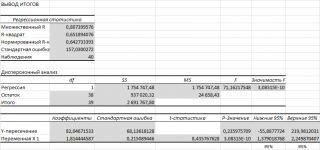
Результаты вычислений, выполненных надстройкой, полностью совпадают с вычислениями сделанными нами в статье про простую линейную регрессию с помощью функций ЛИНЕЙН() , НАКЛОН() , ОТРЕЗОК() и др. Использование альтернативных формул помогает разобраться с алгоритмом расчета показателей регрессии.

Отчет, сформированный надстройкой, состоит из следующих разделов:

Раздел «Регрессионная статистика»:

• Множественный R. В случае простой линейной регрессии — это Коэффициент корреляции , функция КОРРЕЛ()
• R-квадрат . В случае простой линейной регрессии – это коэффициент детерминации , функция КВПИРСОН()
• Нормированный R-квадрат . См. про коэффициент детерминации .
• Стандартная ошибка . См. Стандартная ошибка регрессии ;
• Наблюдения . Количество значений Y.

Раздел « Дисперсионный анализ »:

• df – степени свободы (Degrees of Freedom).
• SS – сумма квадратов (Sum of Squares)
• MS – SS/df (MSR и MSE)
• F – значение статистики F 0 (MSR/MSE)
• ЗначимостьF – p-значение, функция F.РАСП.ПХ()

Другие результаты:

• Коэффициенты : оценка параметров модели а и b. См. Оценка неизвестных параметров .
• Стандартная ошибка : Стандартные ошибки вышеуказанных статистик
• t-статистика : значение тестовой статистики t0. См. Проверка значимости взаимосвязи переменных
• P-Значение : См. Проверка значимости взаимосвязи переменных
• Нижние 95% и Верхние 95%: границы доверительных интервалов для оценок неизвестных параметров модели а и b .

Источник: excel2.ru

Как выполнить простую линейную регрессию в Excel

Простая линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между объясняющей переменной x и переменной отклика y.

В этом руководстве объясняется, как выполнить простую линейную регрессию в Excel.

Пример: простая линейная регрессия в Excel

Предположим, нас интересует взаимосвязь между количеством часов, которое студент тратит на подготовку к экзамену, и полученной им экзаменационной оценкой.

Чтобы исследовать эту взаимосвязь, мы можем выполнить простую линейную регрессию, используя часы обучения в качестве независимой переменной и экзаменационный балл в качестве переменной ответа.

Выполните следующие шаги в Excel, чтобы провести простую линейную регрессию.

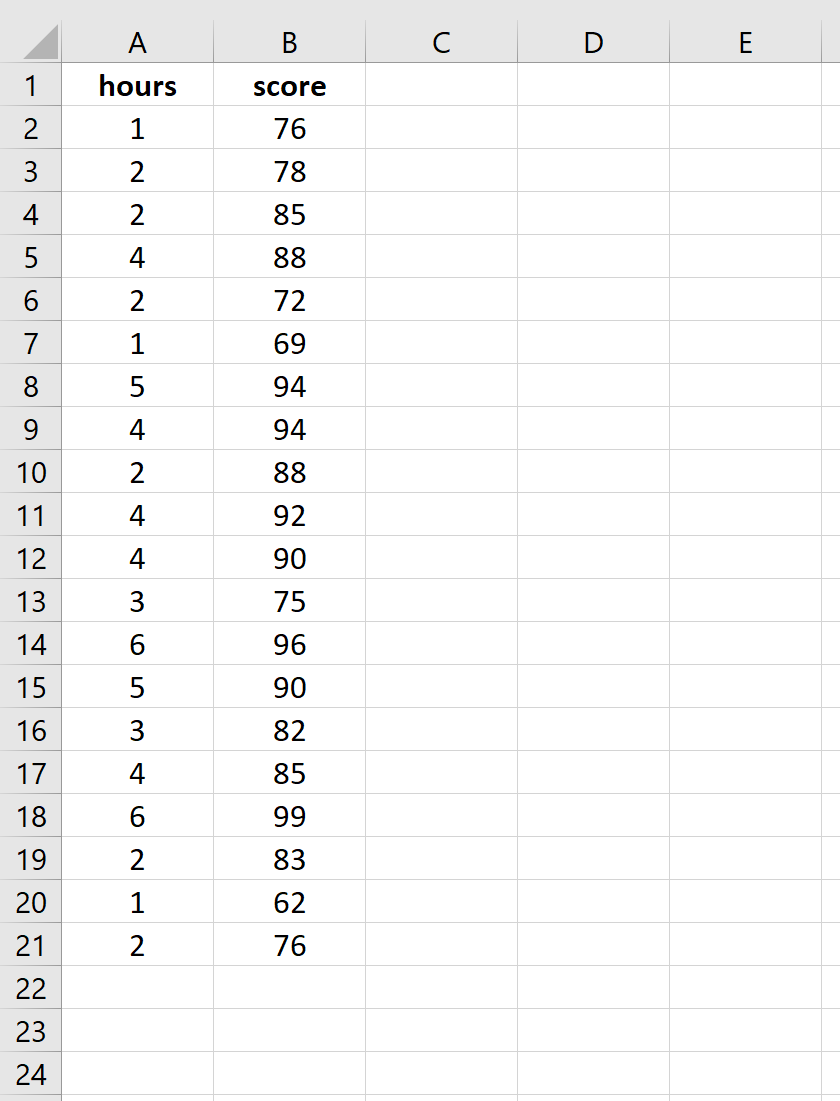
Шаг 1: Введите данные.

Введите следующие данные о количестве часов обучения и экзаменационном балле, полученном для 20 студентов:

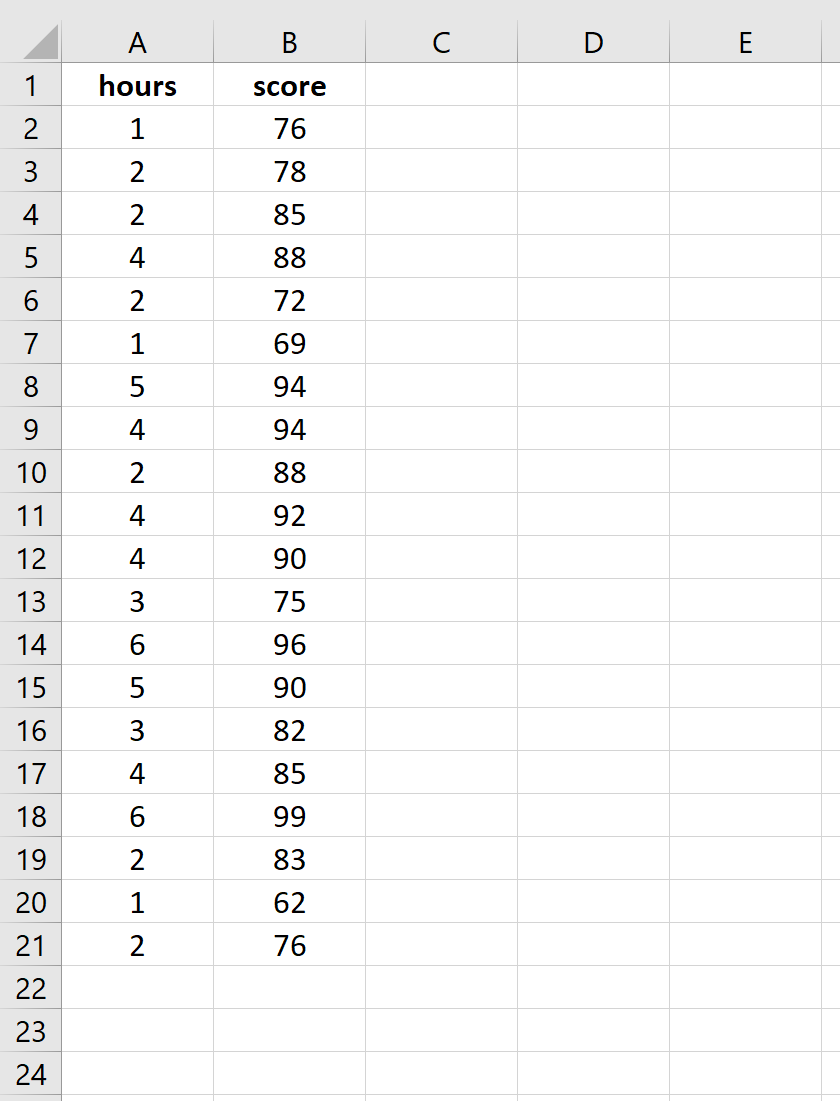
Шаг 2: Визуализируйте данные.

Прежде чем мы выполним простую линейную регрессию, полезно создать диаграмму рассеяния данных, чтобы убедиться, что действительно существует линейная зависимость между отработанными часами и экзаменационным баллом.

Выделите данные в столбцах A и B. В верхней ленте Excel перейдите на вкладку « Вставка ». В группе « Диаграммы » нажмите « Вставить разброс» (X, Y) и выберите первый вариант под названием « Разброс ». Это автоматически создаст следующую диаграмму рассеяния:

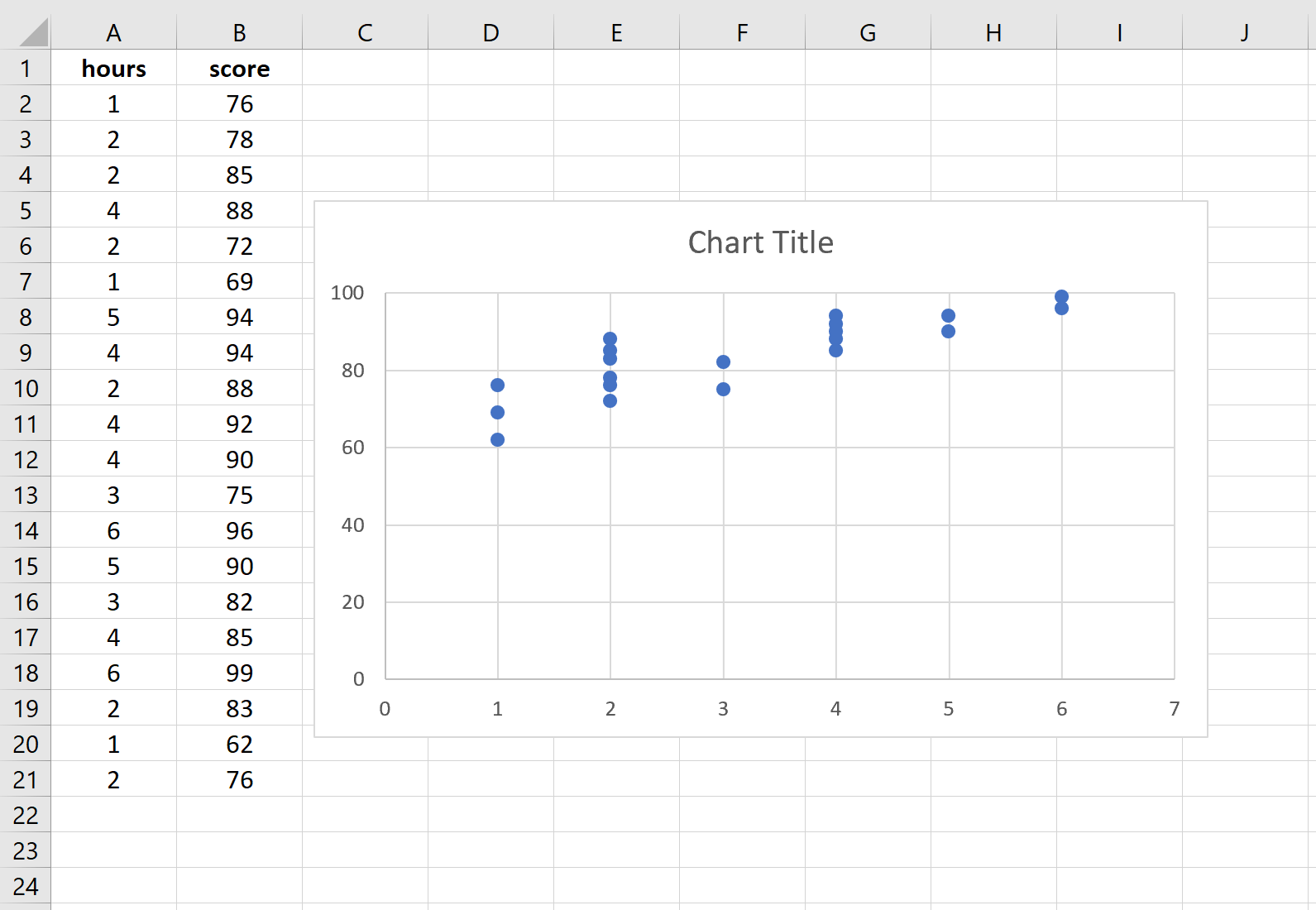
Количество часов обучения показано на оси x, а баллы за экзамены показаны на оси y. Мы видим, что между двумя переменными существует линейная зависимость: большее количество часов обучения связано с более высокими баллами на экзаменах.

Чтобы количественно оценить взаимосвязь между этими двумя переменными, мы можем выполнить простую линейную регрессию.

Шаг 3: Выполните простую линейную регрессию.

В верхней ленте Excel перейдите на вкладку « Данные » и нажмите « Анализ данных».Если вы не видите эту опцию, вам необходимо сначала установить бесплатный пакет инструментов анализа .

Как только вы нажмете « Анализ данных», появится новое окно. Выберите «Регрессия» и нажмите «ОК».

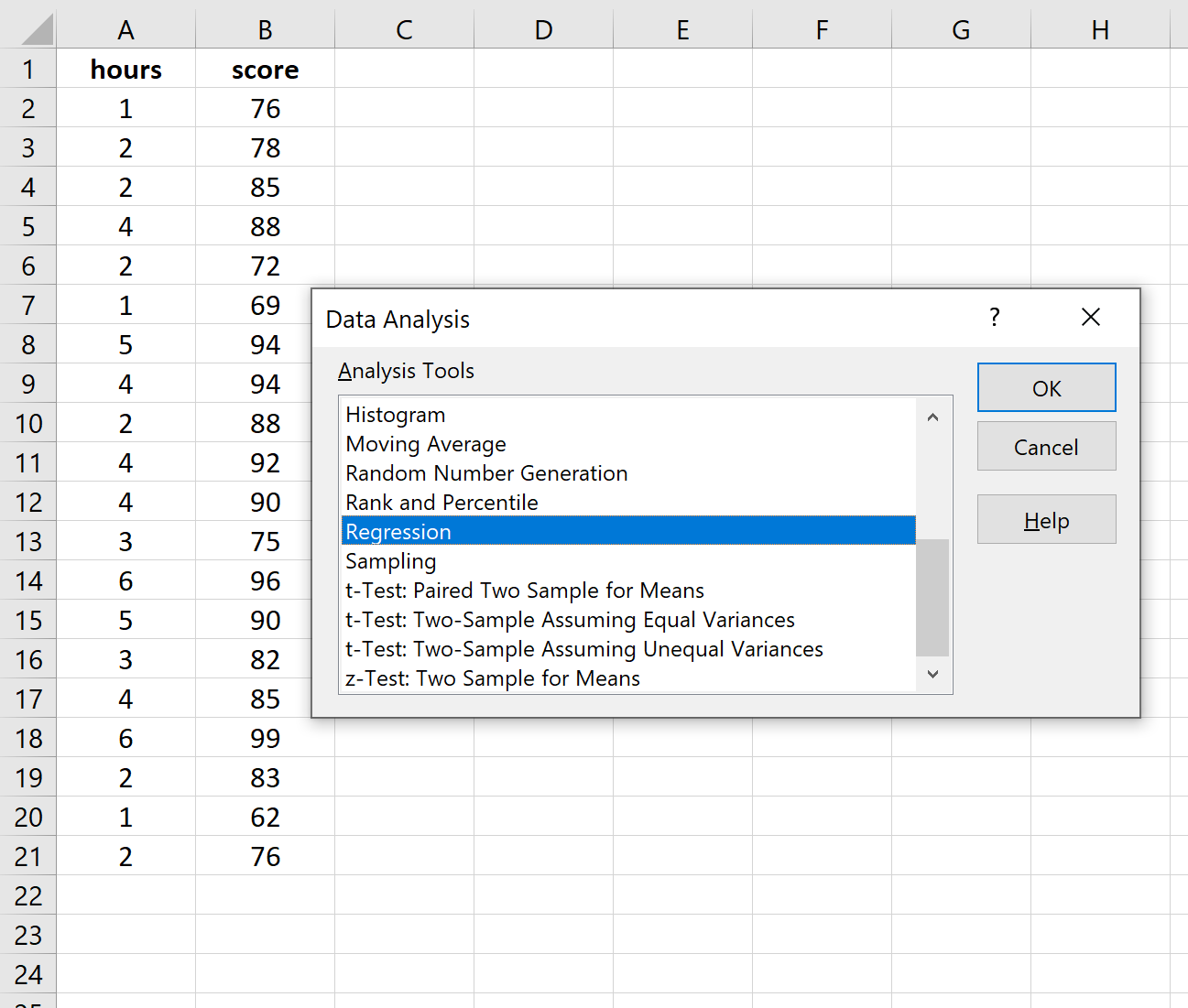
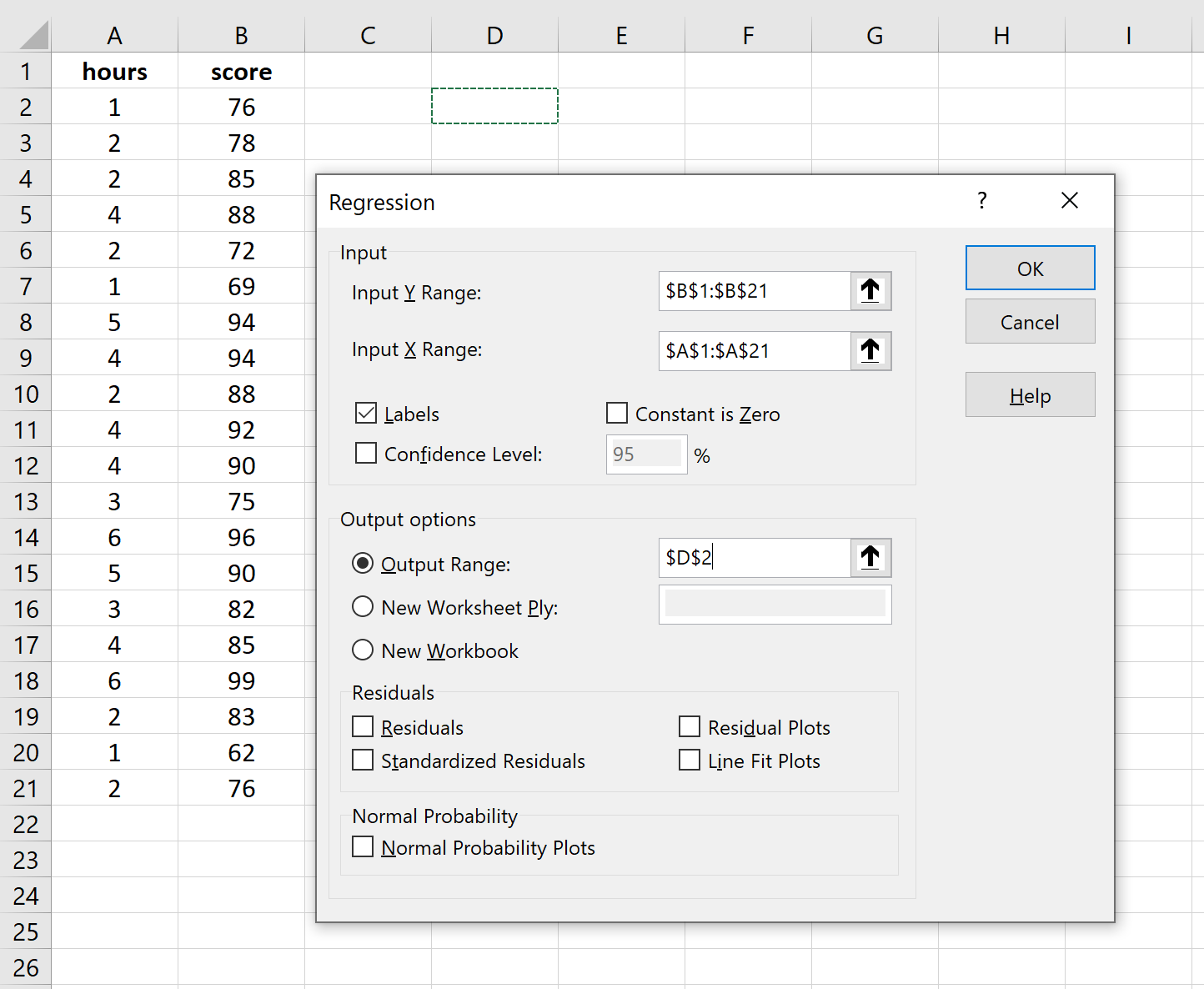
Для Input Y Range заполните массив значений для переменной ответа. Для Input X Range заполните массив значений для независимой переменной.

Установите флажок рядом с Метки , чтобы Excel знал, что мы включили имена переменных во входные диапазоны.

В поле Выходной диапазон выберите ячейку, в которой должны отображаться выходные данные регрессии.

Затем нажмите ОК .

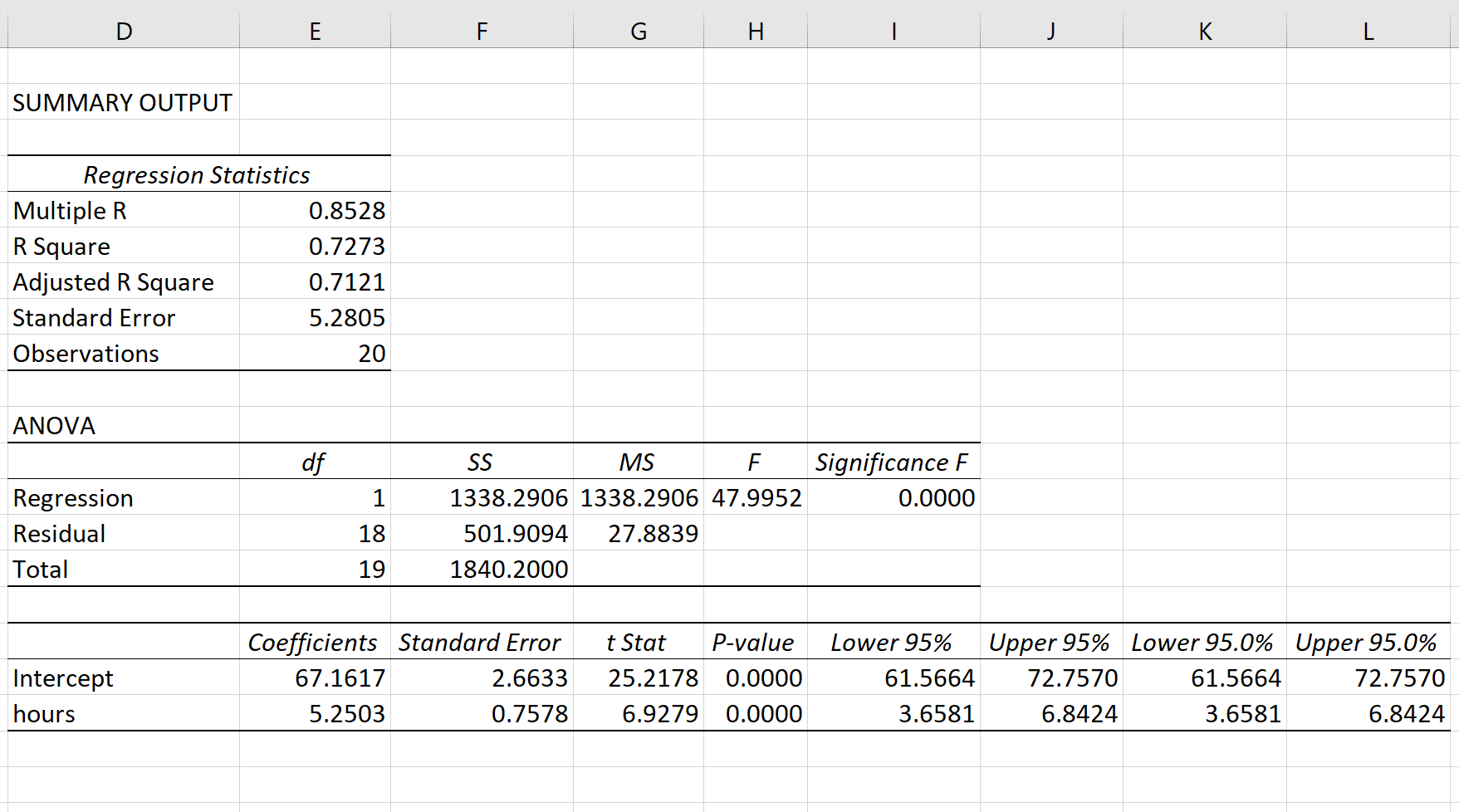
Автоматически появится следующий вывод:

Шаг 4: Интерпретируйте вывод.

Вот как интерпретировать наиболее релевантные числа в выводе:

R-квадрат: 0,7273.Это известно как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющей переменной. В этом примере 72,73 % различий в баллах за экзамены можно объяснить количеством часов обучения.

Стандартная ошибка: 5.2805.Это среднее расстояние, на которое наблюдаемые значения отходят от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,2805 единиц.

Ф: 47,9952.Это общая F-статистика для регрессионной модели, рассчитанная как MS регрессии / остаточная MS.

Значение F: 0,0000.Это p-значение, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель статистически значимой. Другими словами, он говорит нам, имеет ли независимая переменная статистически значимую связь с переменной отклика. В этом случае p-значение меньше 0,05, что указывает на наличие статистически значимой связи между отработанными часами и полученными экзаменационными баллами.

Коэффициенты: коэффициенты дают нам числа, необходимые для написания оценочного уравнения регрессии. В этом примере оцененное уравнение регрессии:

экзаменационный балл = 67,16 + 5,2503*(часов)

Регрессионный анализ в Excel: лучшие практики

Обычно я делаю любой регрессионный анализ на «питоне» – там и данные подготовить проще, и доступны сложные модели. Но простому пользователю (а особенно в учебных целях) нужно что-то попроще. В этой статье я покажу как делать базовый регрессионный анализ в Excel. Все будет просто, понятно, по шагам и с картинками. Поехали!

Эта статья прежде всего про инструмент. Читатель сам должен понимать свои задачи – никакой инструмент за вас это не придумает (ну кроме каких-нибудь разновидностей DQN-сетей при правильном применении ). Поэтому ориентируюсь на новичков в Excel, в мат. статистику не лезу.

Зачем это нужно?

В сложно понимании регрессионный анализ нужен в статистическом исследовании для определения зависимости одной величины от другой в разных разрезах. В практическом смысле (а простого человека интересует именно это) регрессионный анализ помогает сделать предсказание неизвестной величины на основе какого-то предыдущего «опыта». Хотим предсказать курс биткоина на завтра – это примерно об этом, правда, лучше не пытаться.

Шаг 1 – Подготовка данных

Для исследования нам нужно подготовить исходные данные – нам нужно создать два столбца (две величины), на основе которых мы и будем делать регрессионный анализ. Предлагаю простые и понятные данные, где все зависимости вы видите «на глаз». Сложное вы найдете и у себя.

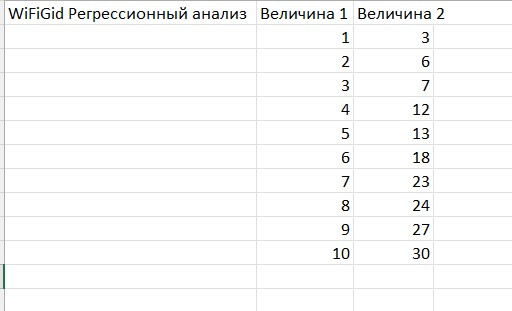
Для учебных целей на представленных данных вторая величина – это всего лишь утроенная первая величина с небольшим шумом, который я добавил вручную.

Шаг 2 – Включаем пакет анализа

По умолчанию пакет анализа, в котором и находится инструмент регрессии, в Excel не включен, поэтому нужно его включить.

Если текст ниже будет совсем непонятным, у нас есть отдельная очень подробная статья по добавлению пакета анализа в Excel.

Файл – Параметры – Надстройки – Надстройки Excel – Кнопка Перейти – Ставим галочку возле «Пакет анализа» – ОК

В результате выполнения этой цепочки действий у вас на вкладке «Данные» в Excel должна появиться кнопка «Анализ данных».

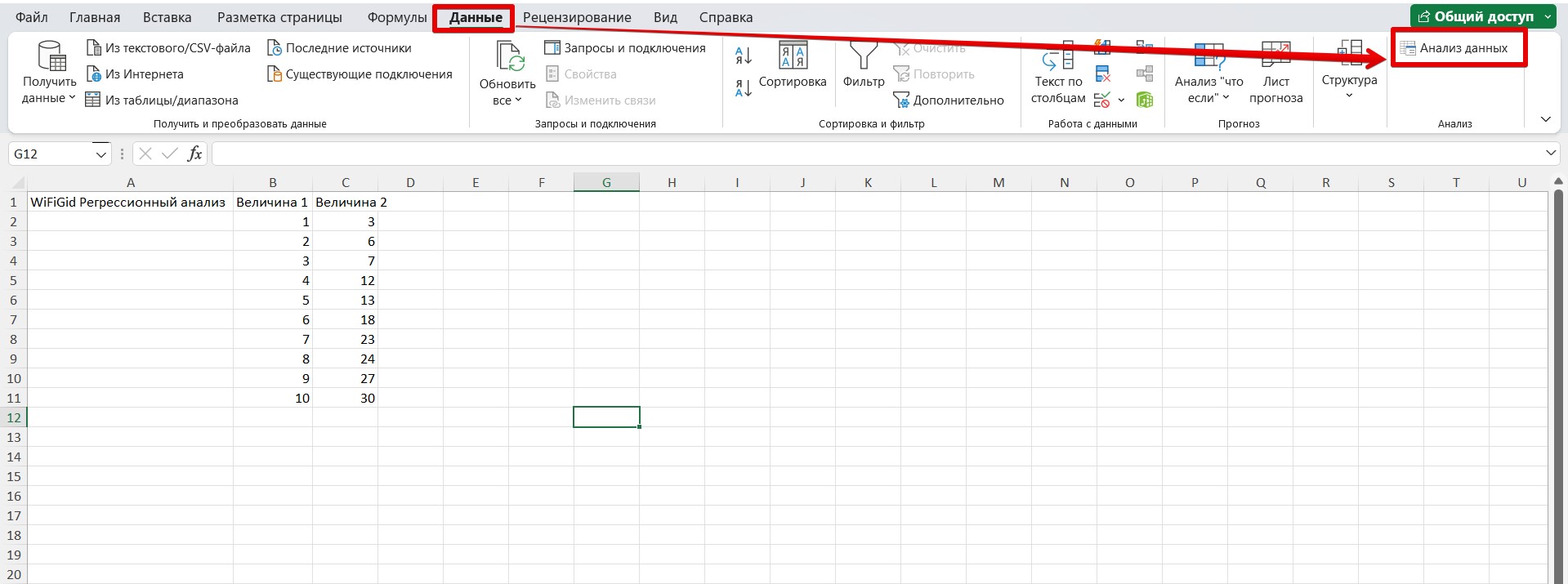
Шаг 3 – Делаем регрессионный анализ

Переходим к самым важным действиям:

1. Нажимаем по той самой кнопке «Анализ данных».
2. В списке находим «Регрессия» и нажимаем ОК.

1. Задаем два входных интервала. Для Y я задам второй столбец, для X – первый. Все остальное можно оставить как есть, тут уже дело под свою конкретную задачу. В том же парном трейдинге для двух коинтегрированных пар очень важно получить график остатков – и тут сразу доступна эта функция. Но в наших учебных целях это не нужно.

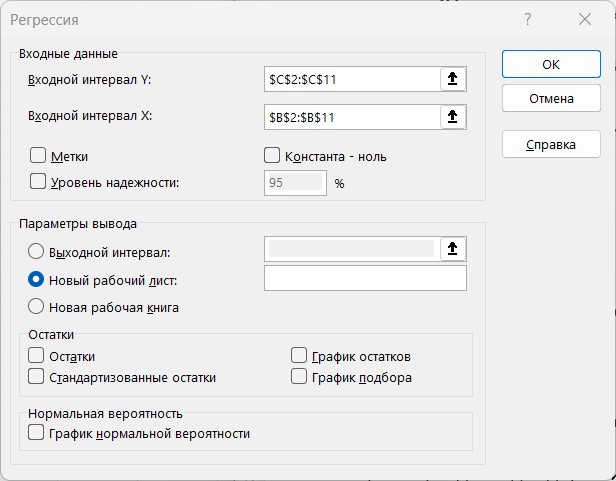
Шаг 4 – Анализ результата

Из статистики вы точно должны знать, раз оказались здесь, что существует много вариантов построения регрессии (степенная, логарифмическая, экспоненциальная и т.д.). Так вот этот способ строит самый простой ее тип – линейную регрессию, т.е. пытается на основе двух величин построить линейную функцию (или просто провести прямую линию через заданные точки на плоскости из двух величин) вида:

Т.е. зная коэффициенты a и b в этом уравнении, на основе первой величины X можно предсказать величину Y. Задача линейной регрессии – найти эти самые коэффициенты a и b. А теперь посмотрим на результаты нашего анализа, которые появились на отдельном листе (все самое важное выделил):

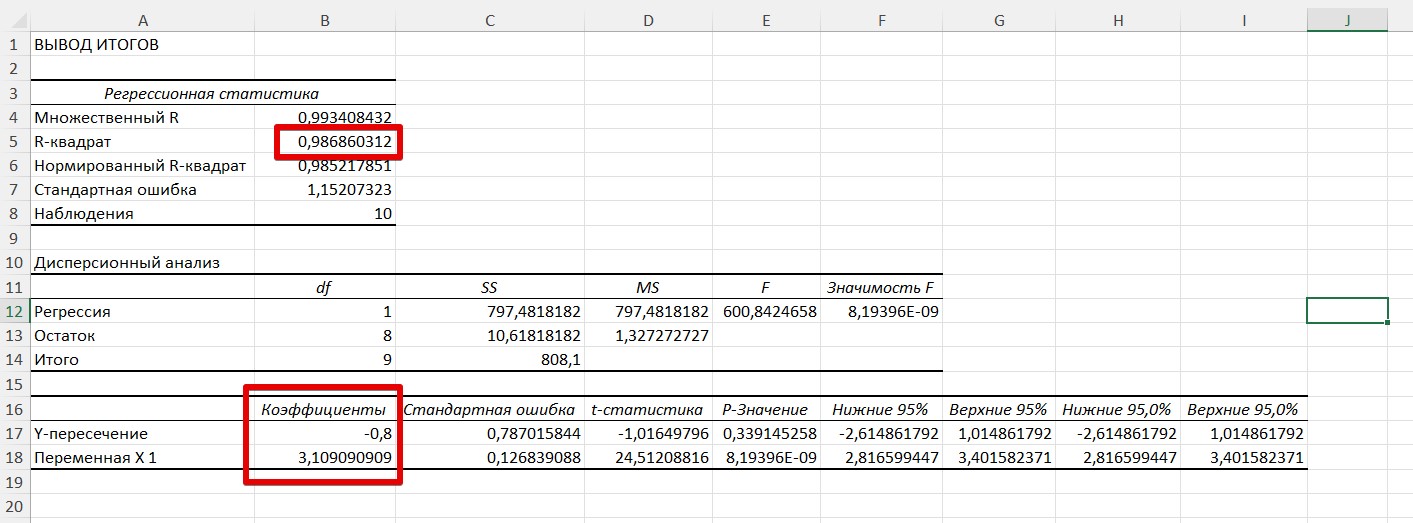
• R-квадрат – мера достоверности нашей модели. Чем ближе к 1, тем лучше. Показывает, насколько хорошо удалось провести линию через заданный массив точек.
• Y-пересечение – коэффициент b в уравнении.
• Переменная X 1 – коэффициент a в уравнении.

Т.е. мы получили отличную зависимость (R-квадрат 0,98, ведь правда же, т.к. она была сразу задана вручную хоть и с шумами), а итоговое уравнение зависимости будет таким:

Немного округлил первый коэффициент, но суть улавливается легко. И кто помнит про линейную функцию, первый коэффициент как раз и показывает основную зависимость первой величины от второй – т.е. здесь разница между ними примерно в 3 раза, как и было задано в начале.

Бонус (быстрый способ) – Строим график

Как и писал выше, подобным в Excel лично я не занимаюсь – руки остаются связанными по всем направлениям. Но построением быстрых графиков в Excel все-таки периодически грешу, тем более здесь есть интересный функционал построения линий регрессий, причем не только линейных.

1. На основе наших двух величин строю простой линейный график (это вы наверняка умеете). Данные использую те же самые.

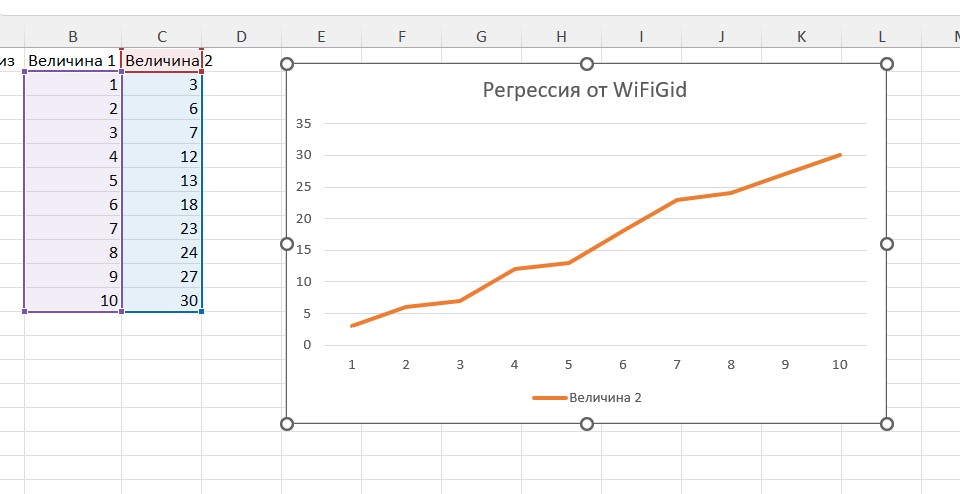
1. Щелкаем ПРАВОЙ кнопкой мыши по самому графику (вот этой оранжевой линии) и выбираем «Добавить линию тренда».

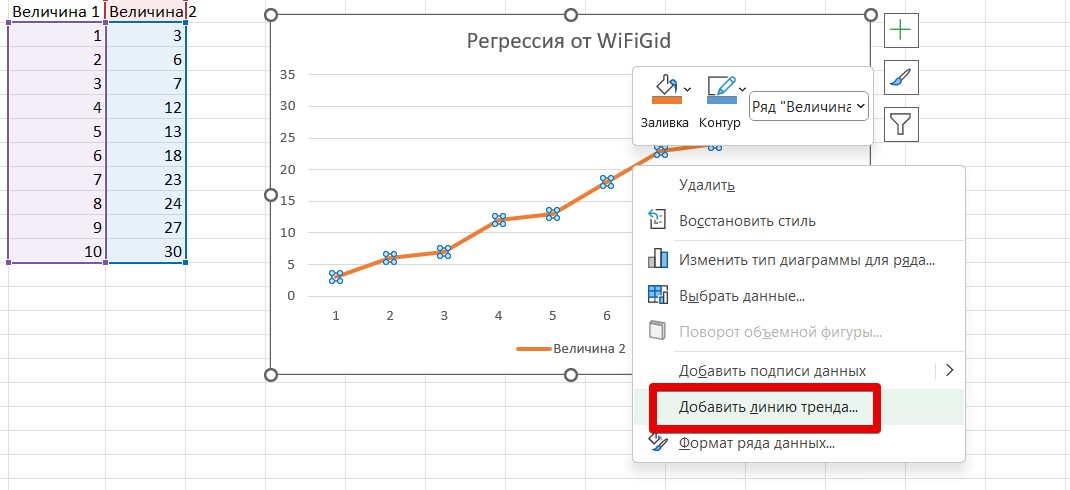
1. В правой части Excel появится список параметров под нашу регрессионную линию. Указываем тип линии тренда – в нашем случае оставляю линейную, но обращаем внимание, что здесь уже доступен расширенный перечень типов. Устанавливаю прогноз «вперед» еще на 10 периодов, а также ставлю галочку отображения уравнения (чтобы сравнить результат с предыдущим пунктом).

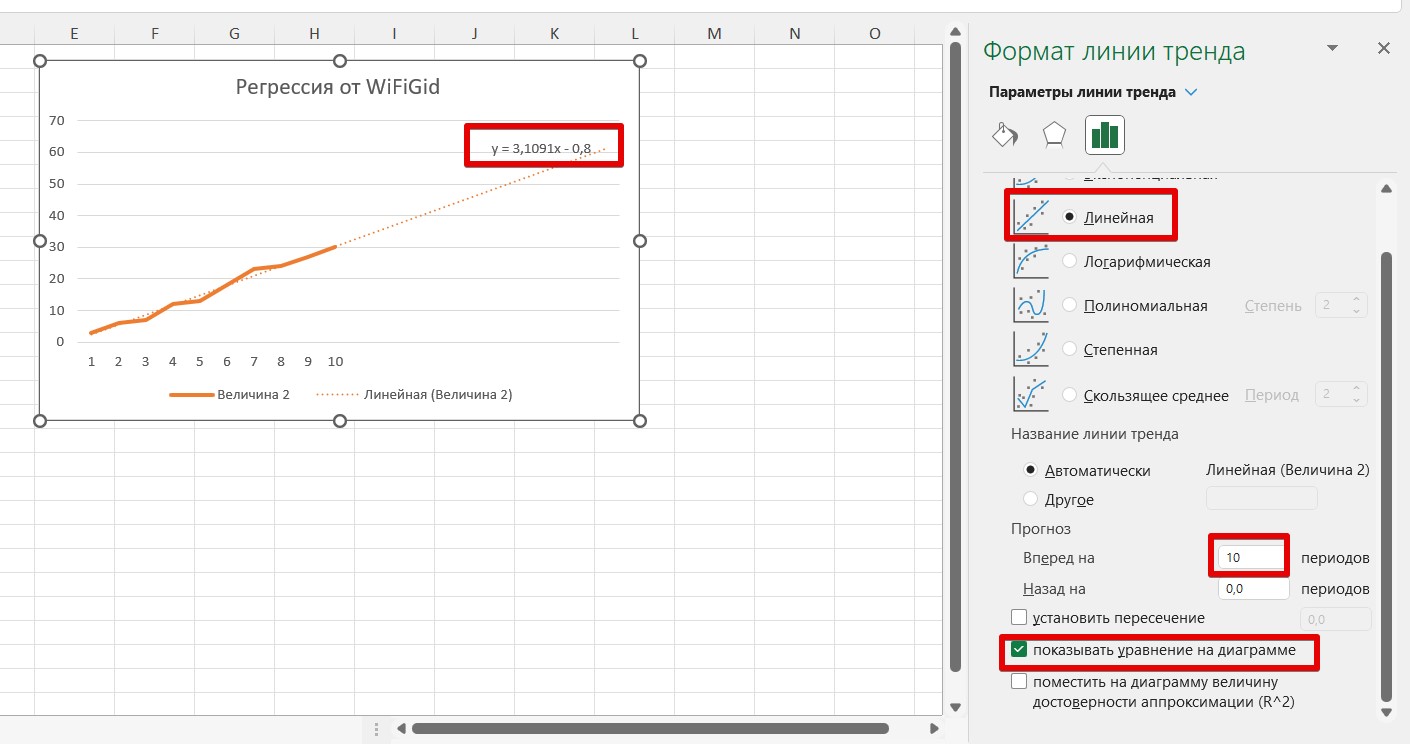
1. Линия строится автоматически, а вместе с ней и уравнение. Обращаем внимание, что уравнение предсказанной линии на графике совпадает с тем, что мы вывели ранее.

Надеюсь, изложил все доступно и понятно. Но еще раз – если нужны сложные расчеты, лучше переходить на профильные языки и среды.

Источник: wifigid.ru