AmLAHX — программа синтеза регуляторов методом желаемых асимптотических ЛАЧХ
Введение. На сегодняшний день существует множество различных методов синтеза регуляторов. Преимуществом метода желаемых логарифмических амплитудно-частотных характеристик (ЛАЧХ) является то, что он позволяет в достаточно полной мере учесть такие требования к желаемой системе управления, как астатизм, точность отработки критического воздействия, перерегулирование и быстродействие. В то же время ориентированность метода на графическое построение ЛАЧХ ограничивает его применение. Автором данный метод синтеза был автоматизирован путем разработки соответствующей программы AmLAHX на языке MatLab [2] .
Общие сведения о методе желаемых ЛАЧХ. При линеаризованном описании передаточная функция разомкнутой системы управления (РС) — это произведение передаточных функций (ПФ) объекта управления (ОУ) и управляющего устройства (УУ) [1]:
При этом ЛАЧХ разомкнутой системы представляет собой сумму характеристик объекта и регулятора, поэтому, имея ЛАЧХ желаемой разомкнутой системы и ЛАЧХ объекта, можно получить ЛАЧХ регулятора простым графическим вычитанием. Сущность метода желаемых ЛАЧХ состоит в следующем. По определенной методике строится желаемая амплитудная характеристика разомкнутой системы. На том же графике строится ЛАЧХ объекта управления, затем графическим вычитанием из ЛАЧХ разомкнутой системы ЛАЧХ объекта получим ЛАЧХ управляющего устройства, по которой определяется его передаточная функция. Ключевым моментом является то, что для упрощения перехода от ЛАЧХ к передаточной функции в расчетах используются асимптотические ЛАЧХ.
ТАУ. Matlab/Simulink — моделирование передаточной функции, снятие характеристик
Общие сведения о программе . Программа AmLAHX предназначена для выполнения в среде MatLab 6 ( R12.1) или выше и предоставляет пользователю следующие возможности:
1. имеет графический интерфейс, отслеживает различные ошибки (случайные или преднамеренные) в процессе работы (в том числе ошибки в исходных данных);
2. строит асимптотические ЛАЧХ динамических объектов, заданных в виде передаточных функций;
3. строит в диалоговом режиме желаемую ЛАЧХ разомкнутой системы по задаваемым критериям качества, в том числе, программа позволяет выбирать пользователю сопрягающие участки (их наклоны) в зависимости от вида ЛАЧХ объекта управления;
4. обеспечивает автоматическое вычитание из ЛАЧХ разомкнутой системы ЛАЧХ объекта управления и построение таким образом ЛАЧХ регулятора, результатом своей работы возвращает сопрягающие частоты и наклоны асимптот ЛАЧХ регулятора и его передаточную функцию;
5. все ЛАЧХ строятся с указанием наклонов асимптот, пользователь может сам определять цвета каждой ЛАЧХ в отдельности, а также формат надписей на графиках (толщина, высота).
Код программы открыт для свободного изменения. Скачать последнюю версию программы можно по адресу в сети Internet http :// videvio.com / amlahx . Текущая версия — AmLAHX 1.1 RC.
Алгоритм работы. В целом программа осуществляет расчеты по следующему алгоритму:
Автоматическое построение передаточных функций в SimInTech.
1. Анализ входных аргументов.
2. Формирование исходных данных (числителя и знаменателя ПФ ОУ) и свойств графиков и надписей в зависимости от режима работы.
3. Формирование массивов структур нулей и полюсов ПФ ОУ.
4. Поиск одинаковых нулей и полюсов и удаление соответствующих структур из массивов.
5. Поиск кратных нулей и полюсов и соответствующая оптимизация массивов структур.
6. Расчет астатизма, наклонов асимптот, коэффициента усиления канонической формы ПФ ОУ.
7. Объединение массивов структур нулей и полюсов, расчет сопрягающих частот и сортировка общего массива по возрастанию величины сопрягающих частот.
8. Построение асимптотической ЛАЧХ.
9. Выход из программы, если выбран 1-й режим работы
10. Ввод критериальной стратегии синтеза (КСС).
11. Получение дополнительной информации о желаемом качесте ЛАЧХ РС по КСС.
12. Построение низкочастотных, среднечастотных и высокочастотных частей ЛАЧХ РС в соответствии с КСС.
13. Ввод наклонов сопрягающих участков.
14. Оптимизация графика желаемой ЛАЧХ РС, исходя из накловно сопрягающих участков.
15. Сортировка сопрягающих частот ЛАЧХ ОУ и ЛАЧХ РС, корректировка дублирования частот и формирование массива структур, описывающего сопрягающие частоты и наклоны асимптот ЛАЧХ УУ.
16. Результат синтеза: график ЛАЧХ и ПФ управляющего устройства.
Командная строка. Полная командная строка для запуска программы имеет вид
[ src, yy , handles ] = amlahx (flag, num , den , prm ) ,
где flag — флаг режима работы (этот и все последующие аргументы могут быть опущены): 1 — построение только ЛАЧХ заданного объекта; 2 — синтез регулятора методом желаемых асимптотических ЛАЧХ (по умолчанию); 3 — вызов меню в начале работы (интерактивный режим);
num, den — соответственно вектора коэффициентов числителя и знаменателя передаточной функции, начиная с коэффициента при старшей степени, степень (порядок) полинома при этом равен количеству элементов вектора минус 1;
prm — структура свойств вида ЛАЧХ. Можно управлять видом ЛАЧХ (цвет, толщина и другое), передав четвертым параметром полную структуру свойств согласно примеру:
prm.oy.Color=’red’; % цвет ЛАЧХ ОУ
prm.oy.LineWidth=1; % толщина ЛАЧХ ОУ
prm.oy.pt=’rp’; % тип соединительных точек в формате ‘plot’
prm.rs.Color=’red’; % цвет ЛАЧХ РС
prm.rs.LineWidth=1; % толщина ЛАЧХ РС
prm.rs.pt=’ko’; % тип соединительных точек в формате ‘plot’
prm.yy.Color=’red’; % цвет ЛАЧХ УУ
prm.yy.LineWidth=2; % толщина ЛАЧХ УУ
prm.yy.pt=»; % тип соединительных точек в формате ‘plot’
amlahx(2,[1 0.2],[100 110 11 1 0],2,prm); % вызов программы
src — структура, полностью описывающая асимптотическую ЛАЧХ ОУ;
yy — структура, полностью описывающая синтезированную асимптотическую ЛАЧХ УУ;
handles—- вектор указателей на созданные графические объекты.
AmLAHX без параметров работает в demo -режиме, в этом случае
num = [1 0.2], den = [100 110 11 1 0], flag = 2.
Режимы работы. AmLAHX имеет 3 режима работы
1. режим построения асимптотической ЛАЧХ ОУ;
2. режим синтеза регулятора (режим по умолчанию);
3. интерактивный режим синтеза регулятора (основной режим).
Для запуска программы в первом режиме в командной строке
MatLab следует набрать amlahx (1, num , den ). В этом режиме программа строит только асимптотическую ЛАЧХ объекта управления (рис. 2). Возвращает программа массив структур src . Структуры описывают динамические звенья, из которых построен ОУ. Каждая структура состоит из 9 полей:
— вещественная ans . a корня числителя или знаменателя;
— мнимая часть ans . b корня (под комплексно-сопряженную пару корней отводится 1 структура);
— кратность ans . krt ;
— вид корня ans . vid (нуль (1) или полюс (-1));
— порядок ans . por корня (1 если корень вещественный, 2 – корень мнимый (то есть имеем комплексно-сопряженную пару корней)):
— параметры динамического звена, имеющего такой корень или такую комплексно-сопряженную пару корней: постоянная времени ans . T , колебательность ans .е, частота среза ans . w , десятичный логарифм частоты среза ans . lgw .
Программа во 2-м и 3-м режимах работы включает все возможности 1-го режима. Функционально 3-й режим отличается от 2-го только возможностью интерактивно задать числитель и знаменатель ПФ ОУ, а также параметры графиков, поэтому рассмотрим подробнее именно работу в 3-м режиме на примере синтеза регулятора для объекта
В командной строке MatLab набираем
amlahx (3,[1 0.2], [100 110 11 1 0]).
Сразу после запуска программы появляется «Главное меню»
(рис . 1). В надписях в этом и других окнах программы буква ‘ я ‘ заменена на ‘ ь ‘ для обеспечения совместимости с различными реализациями MatLab , некоторые из которых выдают ошибку при наличии в коде букв ‘ я ‘. Меню формируется функцией k = umenu( Title, pos , xHeader , varargin ), которая является модификацией поставляемой с MatLab функцией ‘menu’ и отличается от нее возможностью через входные аргументы задавать заголовок Title и положение pos окна c меню.
Рис. 1. Главное меню AmLAHX .
Опишем основные пункты меню. Пункты ‘ Ввести числитель/знаменатель передаточной функции объекта ‘ дают возможность ввести числитель и знаменатель в интерактивном режиме. Если на каком-то шаге ввод будет прерван, а в командной строке в начале работы AmLAHX были переданы коэффициенты числителя/знаменателя, то числитель/знаменатель все равно считается заданным. При выборе этих пунктов открывается меню (рис. 2).

Рис.2. Меню ввода исходных данных.
При выборе первого пункта этого меню у пользователя запрашивается порядок полинома, после чего открывает окно интерактивного ввода коэффициентов полинома, реализуемого с помощью функции
[M, outstr] = uniinput(SM, FStr, mflg, TUIStr, Req, MMVal), которая входит в дистрибутив программы AmLAHX . Функция ‘uniinput’ может быть использована отдельно от AmLAHX в качестве удобного средства для ввода матриц, векторов и полиномов. Для полинома 3 порядка вид окна приведен на рис.3.
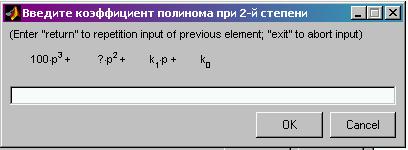
Рис.3. Окно ввода коэффициентов полинома.
Каждый коэффициент полинома вводится поочередно с отображением на экране. Вводимому в данный момент коэффициенту соответствует знак ‘?’. Для повторного ввода в случае ошибки следует набрать ‘return’ . Вывод на экран полинома в привычном формате осуществляется путем присвоения свойству окна ‘Interpreter’ значения ‘tex’ (использование для интерпретатора TeX для выводимых на экран сообщений) . По окончании ввода полином выводится на экран (рис.4).
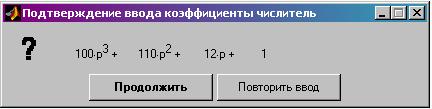
Рис.4. Окно подтверждения ввода коэффициентов полинома.
Пункт главного меню ‘ Настройки ‘ позволять задать цвета и толщину графиков (рис.5) при условии, что в начале работы не был задан аргумент prm, в противном случае, все изменения в «Настройках» не будут иметь силы. Начальные настройки читаются из файла ‘ amlahx.ini ‘ , причем, все внесенные изменения действуют только в данном сеансе работы, поэтому, чтобы изменить начальные настройки, необходимо отредактировать соответствующим образом файл ‘ amlahx.ini ‘.
Пункт ‘ Продолжить ‘ — продолжение работы при условии, что через меню или командную строку заданы полиномы числителя и знаменателя ПФ ОУ, иначе выдается предупреждающее сообщение.
После выбора пункта ‘ Продолжить ‘ выполняется автоматическое построение ЛАЧХ ОУ с указанием наклонов (см. рис. 8). Если объект идеальный (порядок числителя больше порядка знаменателя) пользователю предлагается остановиться и задать реальный объект. В ходе расчетов программа находит кратные корни в числителе и знаменателе, а также находит и удаляет одинаковые корни числителя и знаменателя. Результатом расчетов является описанный выше массив структур spc .

Рис.5. Окно ‘ Настройки AmLAHX’ .
После построения ЛАЧХ ОУ открывается окно задания критериальной стратегии синтеза (рис . 6 ). Задаем степень астатизма = — 2, желаемое время регулирования = 40 сек, коэффициент усиления РС k = 2,
желаемое перерегулирование s = 20 %.
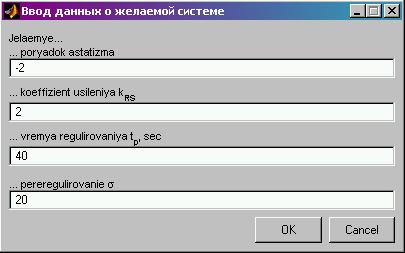
Рис . 6 . Окно ввода параметров желаемой РС .
Далее по номограммам, исходя из и s , пользователь должен указать желаемую частоту среза (частота на которой СЧ-часть желаемой ЛАЧХ пересекает ось частот) и допустимою величину отклонения ЛАЧХ на СЧ-части D l и D φ . В данном примере = 0.35 , D l = ±20 дБ (рис.7).
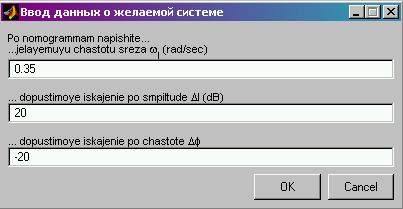
Рис.7. Окно ввода параметров, определяемых по номограммам.
Программа выполняет необходимые расчеты и строит НЧ- и СЧ-части желаемой ЛАЧХ с указанием наклонов, после чего запрашивает у пользователя желаемый наклон отрезка, сопрягающего НЧ- и СЧ-части. Выберем наклон — 60 дБ/дек.
Заключительный этап работы программы — вычитание из ЛАЧХ РС ЛАЧХ ОУ и получение таким образом ЛАЧХ УУ. Этот этап состоит из двух шагов. Первый шаг — расчет массива структур yy , соответствующего ЛАЧХ регулятора. Эти структуры описывают сопрягающие частоты и наклоны асимптот на них. Каждая структура состоит из 5 полей:
— десятичный логарифм сопрягающей частоты ans . lgw ;
— наклон асимптоты на этой частоте ans . nakl ;
— порядок и вид динамического звена ans . por , соответствующего данной сопрягающей частоте (например, если для сопрягающей частоты известно, что порядок динамического звена равен 2, это означает, что это либо 2 пропорциально-дифференцирующих (ПД) звена, либо ПД-звено 2-го порядка);
— сопрягающая частота ans.w;
— постоянная времени динамического звена ans . T .
Второй шаг — по рассчитанной структуре строится ЛАЧХ регулятора. На этом работа программы завершается. На заключительном графике программа строит 3 ЛАЧХ: ОУ, РС, УУ с указанием наклонов (рис.8) и в окне выводит ПФ синтезированного регулятора (рис. 9).
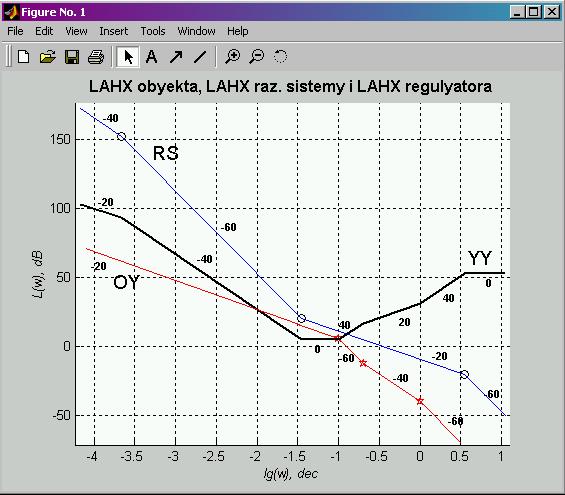
Рис. 8. Окно с построенными ЛАЧХ ОУ, РС и УУ.
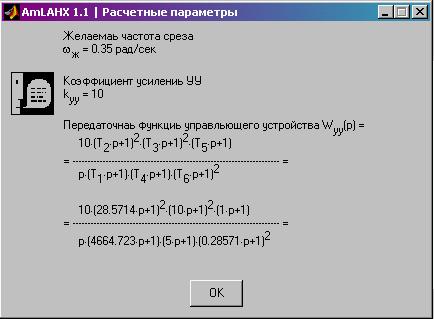
Рис. 9. Окно с информацией о синтезированном регуляторе .
Выводы. Рассмотренная программа была применена автором в бакалаврской работе [3] для синтеза регулятора контура тока в системе управления электроприводом с такими критериями качества: желаемое время регулирования 0.3 сек; степень астатизма — 1; точность отработки критического воздействия £ 0.05; желаемое перерегулирование 5 %. ЛАЧХ объекта управления разомкнутой системы и итоговая ЛАЧХ регулятора, построенные с помощью AmLAHX , а также переходные процессы в контуре тока с регулятором и без него изображены на рис.
10. Благодаря регулятору контур тока отвечает всем заданным критериям качества (как можно видеть из рис. 10, переходный процесс в контуре тока стал апериодичным, при этом быстродействие не изменилось). Планируется использовать AmLAHX в учебном процессе при изучении метода желаемых ЛАЧХ в курсе «Синтез законов управления».
В последующих версиях предполагается дополнить программу средствами анализа системы управления с синтезированным регулятором.
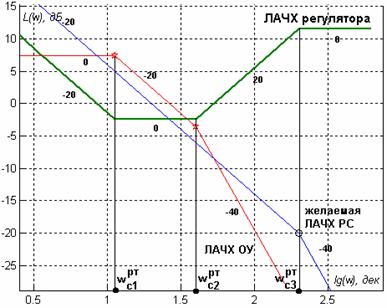
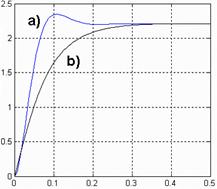
Рис. 10. ЛАЧХ регулятора тока (слева) и переходные процессы в контуре тока без регулятора (а) с регулятором ( b ).
2 . Дьяконов В.П. MatLab 6: учебный курс. — СПб.: Питер, 2001. — 592 с.: ил.
3. Груздев В.В. Автоматизация синтеза регуляторов методом желаемых ЛАЧХ. Конференция. IV Межрегиональная научно-практическая конференция. Материалы конференции. с.60-62.
Источник: videvio.com
Использование обратного преобразования Лапласа для анализа динамических звеньев систем управления
До настоящего времени в арсенале средств высокоуровневого языка программирования Python отсутствовали модули для численного преобразования передаточных функций элементов САУ из частотной области во временную.
Поскольку функции обратного преобразования Лапласа широко используются при анализе динамических систем контроля измерения и управления, использование Python для указанных целей было весьма затруднительно, поскольку приходилось использовать менее точное обратное Фурье преобразование [1].
Указанную проблему решает модуль mpmath библиотеки Python свободного распространения (под лицензией BSD), предназначенный для решения задач вещественной и комплексной арифметики с плавающей точкой и заданной точностью.
Работу над модулем ещё в 2007 году начал Fredrik Johansson [2], и, благодаря помощи многих участников проекта, в настоящее время mpmath приобрёл возможности серьёзного математического пакета.
Однако нас будет интересовать только заявленная в статье тема, реализуемая при помощи одношагового алгоритма invertlaplace. В качестве примера рассмотрим сравнение результатов обратного преобразования Лапласа передаточной функции w(p)=1/(1+p)** 2 при помощи invertlaplace с известной переходной функцией h(t)=e**-t от указанной передаточной функции:
Тестирование invertlaplace
from mpmath import * import time mp.dps = 15#число членов, используемых в приближении mp.pretty = True start = time.time() def run_invertlaplace(tt,fp,ft): for i in range(0,len(tt)): print(‘Значение тестовой функции : %s’%ft(tt[i])) print(‘Полученное значение функции : %s’%invertlaplace(fp,tt[i],method=’talbot’)) print(‘ Значение h(t) : %s. Абсолютная погрешность :%s.’%(ft(tt[i]), ft(tt[i])-invertlaplace(fp,tt[i],method=’talbot’))) stop = time.time() print («Время, затраченное на обратное преобразование Лапласа: %s»%(stop-start)) tt = [0.001, 0.01, 0.1, 1, 10]#список значений отсчётов времени fp = lambda p: 1/(p+1)**2#передаточная функция частоты для тестирования программы ft = lambda t: t*exp(-t)# переходная функция времени для тестирования программы run_invertlaplace(tt,fp,ft)
Значение тестовой функции: 0.000999000499833375
Полученное значение функции: 0.000999000499833375
Значение h(t): 0.000999000499833375. Абсолютная погрешность :8.57923043561212e-20.
Значение тестовой функции: 0.00990049833749168
Полученное значение функции: 0.00990049833749168
Значение h(t): 0.00990049833749168. Абсолютная погрешность :3.27007646698047e-19.
Значение тестовой функции: 0.090483741803596
Полученное значение функции: 0.090483741803596
Значение h(t): 0.090483741803596. Абсолютная погрешность: -1.75215800052168e-18.
Значение тестовой функции: 0.367879441171442
Полученное значение функции: 0.367879441171442
Значение h(t): 0.367879441171442. Абсолютная погрешность :1.2428864009344e-17.
Значение тестовой функции: 0.000453999297624849
Полученное значение функции: 0.000453999297624849
Значение h(t): 0.000453999297624849. Абсолютная погрешность :4.04513489306658e-20.
Время, затраченное на обратное преобразование Лапласа: 0.18808794021606445
Тестовый пример ограничен по объёму, но и на нём видно, что одношаговый алгоритм invertlaplace имеет высокую точность и не критичное время выполнения для ограниченного числа значений времени.
В рассмотренном примере был использован метод talbot, об особенностях других методов можно прочесть в документации [3].
Однако следует учитывать, что все численные методы обратного преобразования Лапласа требуют, чтобы их абсцисса сдвигалась ближе к началу координат для больших времен. Если абсцисса сдвинется влево от самой правой координаты в области Лапласа, ответ будет совершенно неверным.
Поэтому необходимо провести исследование применимости численного обратного преобразования Лапласа для определённых передаточных функций и оценить погрешность в сравнении с другим методом, в данной публикации это метод обратного преобразования Фурье.
1. Построение переходной характеристики объекта управления по его передаточной функции с использованием invertlaplace
Допустим, у нас есть водно-водяной теплообменник с передаточной функцией по каналу, температура нагреваемой воды – расход греющей воды.Преобразование Лапласа выходного сигнала — передаточная функция объекта управления умноженная на 1/p (единичного возмущения по расходу греющей воды) с учётом запаздывания τ имеет следующий вид:
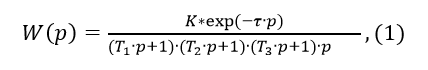
где: Ti – постоянные времени звеньев; K – статический коэффициент передачи; p ¬ оператор Лапласа.
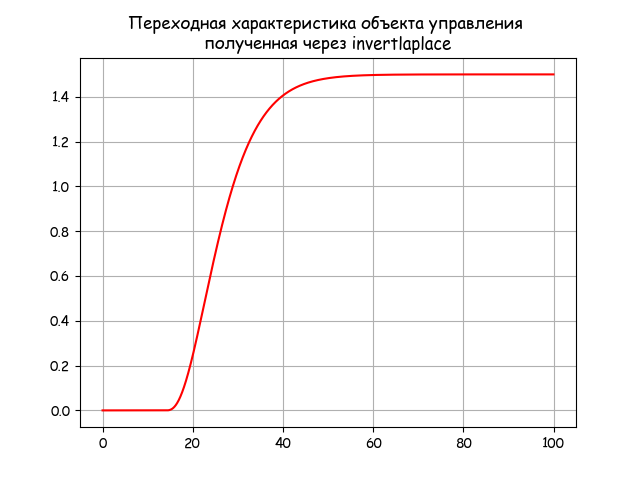
Обратное преобразование Лапласа передаточной функции(1)
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams[‘font.family’] = ‘fantasy’ mpl.rcParams[‘font.fantasy’] = ‘Comic Sans MS, Arial’ mp.dps = 5; mp.pretty = True def run_invertlaplace(tt,fp,tau): y=[] for i in np.arange(0,len(tt)): if tt[i]
Получим переходную характеристику объекта с запаздыванием и самовыравниванием:
2. Построение переходной характеристики ПИД- регулятора по его передаточной функции с использованием invertlaplace
Изображение по Лапласу передаточной функции ПИД регулятора имеет вид:
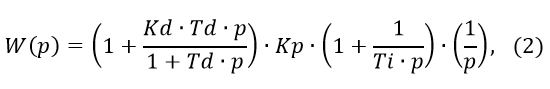
где: Td, Ti – постоянные времени, дифференцирующего и интегрирующего звеньев; Kp, Kd – статические коэффициенты передачи пропорционального и дифференцирующего звеньев;
p – оператор Лапласа.
Обратное преобразование Лапласа передаточной функции(2)
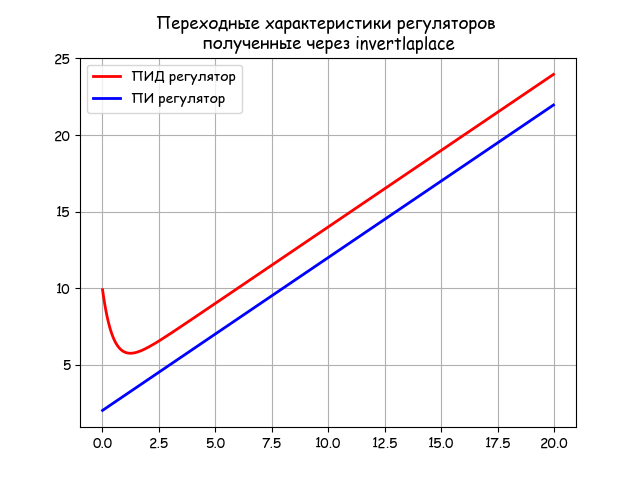
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams[‘font.family’] = ‘fantasy’ mpl.rcParams[‘font.fantasy’] = ‘Comic Sans MS, Arial’ mp.dps = 5; mp.pretty = True tt = np.arange(0.01,20,0.05) Kp=2;Ti=2;Kd=4;Td=0.5 fp = lambda p: (1+(Kd*Td*p)/(1+Td*p))*Kp*(1+1/(Ti*p))*(1/p) y=[invertlaplace(fp,tt[i],method=’talbot’) for i in np.arange(0,len(tt))] Kd=0 fp = lambda p: (1+(Kd*Td*p)/(1+Td*p))*Kp*(1+1/(Ti*p))*(1/p) y1=[invertlaplace(fp,tt[i],method=’talbot’) for i in np.arange(0,len(tt))] plt.title(‘Переходные характеристики регуляторов n, полученные через invertlaplace ‘) plt.plot(tt,y,’r’, color=’r’,linewidth=2, label=’ПИД-регулятор’) plt.plot(tt,y1, color=’b’, linewidth=2, label=’ПИ-регулятор’) plt.grid(True) plt.legend(loc=’best’) plt.show()
По приведенному листингу можно получить не только переходную характеристику ПИД- регулятора, но и ПИ-регулятора, приняв Kd=0:
3. Оценка точности численного метода обратного преобразования Лапласа invertlaplace применительно к типовым объектам САУ
С учётом предостережений относительно применимости invertlaplace, приведенных в начале статьи, в дальнейшем изложении была доказана применимость метода к объектам с запаздыванием и самовыравниванием, а так же к регуляторам.
Остаётся до конца не выясненным вопрос точности численного решения. Для внесения ясности воспользуемся передаточной функцией (2) и следующим точным её преобразованием в переходную функцию, приведённую в [1]:
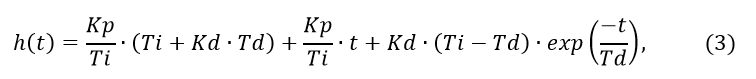
Точность обратного преобразования (2) с использованием тестовой функции (3)
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams[‘font.family’] = ‘fantasy’ mpl.rcParams[‘font.fantasy’] = ‘Comic Sans MS, Arial’ mp.dps = 15; mp.pretty = True tt = np.arange(0.01,20,0.01) Kp=2;Ti=2;Kd=4;Td=0.5 fp = lambda p: (1+(Kd*Td*p)/(1+Td*p))*Kp*(1+1/(Ti*p))*(1/p) ft = lambda t:(Kp/Ti)*(Ti+Kd*Td)+(Kp/Ti)*t+Kd*(Ti-Td)*exp(-t/Td) y=np.array([invertlaplace(fp,tt[i],method=’talbot’) for i in np.arange(0,len(tt))]) y1=np.array([ft(tt[i]) for i in np.arange(0,len(tt))]) z=y-y1 plt.title(‘Оценка точности invertlaplace ‘) plt.plot(tt,z,’r’, color=’r’,linewidth=1, label=’Разница между точным и численным решением’) plt.grid(True) plt.legend(loc=’best’) plt.show()
Получим следующий график:
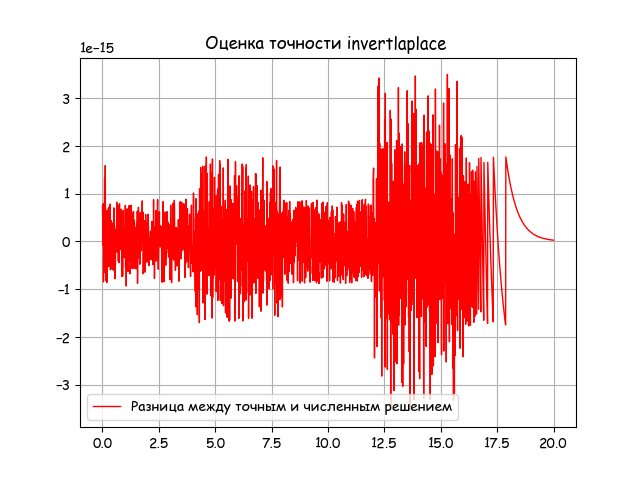
Из графика видно, что погрешность численного метода для приведенного класса передаточных функций пренебрежимо мала (3*10^-15). Кроме того, погрешностью численного метода можно управлять, устанавливая значения mp.dps и шаг tt[i+1]-tt[i] (см. листинг).
4. Сравнительная оценка точности численного метода обратного преобразования Лапласа invertlaplace и численного метода обратного преобразования Фурье применительно к типовым объектам САУ
Построение переходной характеристики можно произвести на основе формулы обратного преобразования Фурье [1]:
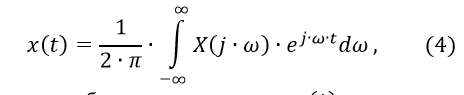
где X(j∙ω)— Фурье-изображение оригинала x(t)
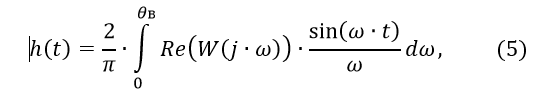
где Re(W(j∙ω))— вещественная частотная характеристика объекта регулирования.
В качестве верхнего предела интегрирования θв в расчете берется значение частоты ωс, при котором модуль Re(W(j∙ω)) уменьшается до некоторого малого значения (например, 0,05*K) и не превосходит это значение при дальнейшем возрастании ω.
Вначале определим верхний предел интегрирования в соотношении (5). Для этого воспользуемся передаточной функцией (1), предварительно избавившись от единичного воздействия, умножив правую часть на оператор p.
Построение графика функции Re(W(j∙ω))
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams[‘font.family’] = ‘fantasy’ mpl.rcParams[‘font.fantasy’] = ‘Comic Sans MS, Arial’ ww= np.arange(0,0.6,0.005) T1=25;T2=21;T3=12;K=0.37;tau=14 def invertfure(w): j=(-1)**0.5 return ((K*np.exp(-tau*j*w)/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))).real) z=[invertfure(w) for w in ww] plt.title(‘Зависимость вещественной части передаточной функции n объекта управления Re(W(j*w)) от частоты ‘) plt.plot(ww,z,’r’) plt.grid(True) plt.show()
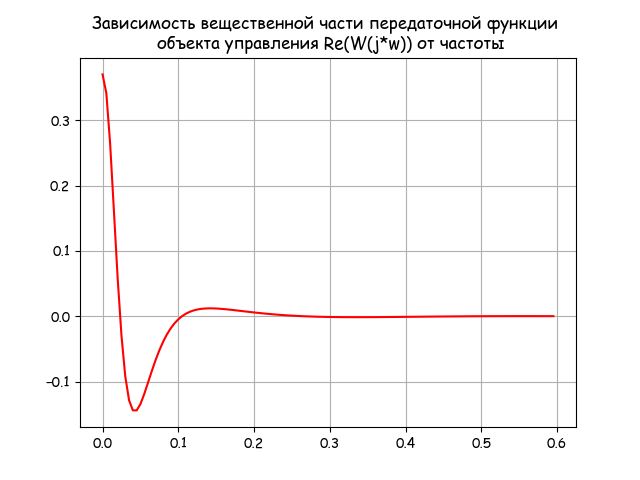
Из графика видно, что верхний предел интегрирования в соотношении (5) может быть принят равным 0.6, поскольку при дальнейшем увеличении частоты вещественная часть передаточной функции объекта управления сохраняет нулевое значение.
Используя (5), получим переходную характеристику объекта управления методом обратного преобразования Фурье:
Переходная характеристика по Фурье
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams[‘font.family’] = ‘fantasy’ mpl.rcParams[‘font.fantasy’] = ‘Comic Sans MS, Arial’ from scipy.integrate import quad tt=np.arange(0,200,1) T1=25;T2=21;T3=12;K=0.37;tau=14 def invertfure(w,t): j=(-1)**0.5 return (2/np.pi)*((K*np.exp(-tau*j*w)/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))).real*(np.sin(w*t)/w)) z=[quad(lambda w: invertfure(w,t),0, 0.6)[0] for t in tt] plt.title(‘Переходная характеристика объекта управления, полученная n методом обратного преобразования Фурье’) plt.plot(tt,z,’r’) plt.grid(True) plt.show()
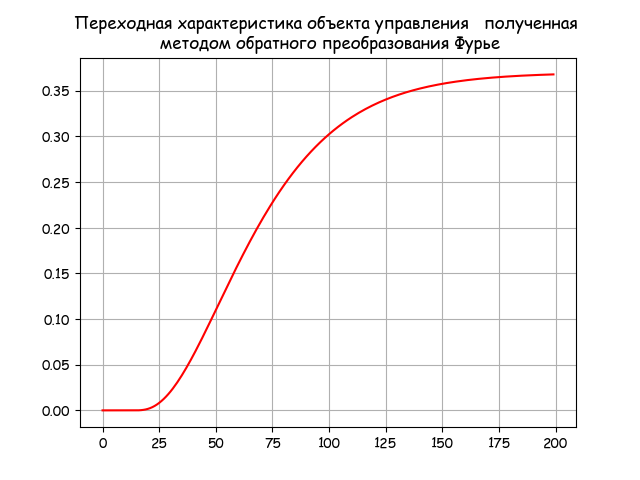
Для сравнительной оценки точности обратного преобразования Лапласа и Фурье, воспользуемся точным преобразованием передаточной функции (1) объекта управления приведенном в [1]:
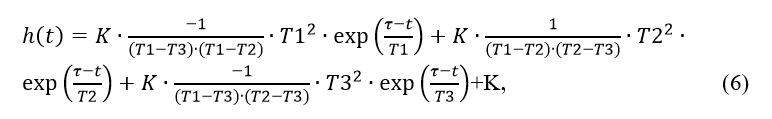
Из точного преобразования (6) вычтем по очереди обратное преобразование (1) Лапласа и обратное преобразование Фурье. Для построения графика, характеризующего сравнение точности обеих методов, составим следующий листинг программы:
Сравнительный анализ методов обратного преобразования Лапласа и Фурье
# -*- coding: utf8 -*- import numpy as np from scipy.integrate import quad import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams[‘font.family’] = ‘fantasy’ mpl.rcParams[‘font.fantasy’] = ‘Comic Sans MS, Arial’ tt = np.arange(0,100,0.01) T1=25;T2=21;T3=12;K=0.37;tau=14 def invertfure(w,t): j=(-1)**0.5 return (2/np.pi)*((K*np.exp(-tau*j*w)/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))).real*(np.sin(w*t)/w)) z=np.array([quad(lambda w: invertfure(w,t),0, 0.6)[0] for t in tt]) def h(t): if t
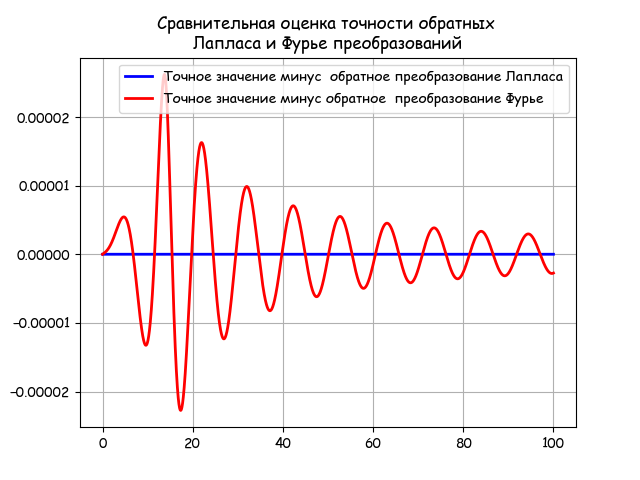
Из графика следует, что численное обратное преобразование Лапласа является более стабильным, чем Фурье и, кроме этого, оно совпадает с точным решением.
Выводы
1. Проведен сравнительный анализ численных методов обратного преобразования Лапласа и Фурье, показана большая точность и стабильность обратного преобразования Лапласа.
2. Показаны возможности применения библиотеки mpmath Python для обратного преобразования Лапласа основных передаточных функций объектов и элементов САУ.
Ссылки
- Расчёт и моделирование автоматических систем регулирования в среде Mathcad.
- Fredrik Johansson.
- Numerical inverse Laplace transform.
- Объекты САУ
- переходные и передаточные функции
- обратное преобразование Лапласа
- обратное
- преобразование Лапласа
Источник: habr.com
Программа для построения передаточной функции
Описываются функциональные возможности калькулятора передаточных функций регулируемых объектов: сложение, умножение, вычитание и деление, обратные преобразования, нахождение аналитических выражений передаточных функций и построение их графиков.

Цель работы – усовершенствовать и добавить новые функции в существующий калькулятор передаточных функций в среде программирования Borland Delphi версии 5 [1]. Калькулятор создан на кафедре АТП БФ ПГТУ, предназначен для выполнения арифметических операций с передаточными функциями без запаздывания и используется для практических занятий по курсам «Теория управления» и «Автоматизация технологических процессов», а также в курсовом и дипломном проектировании студентами специальности «Автоматизация технологических процессов».
В отличие от обычного калькулятора, где математические операции производятся над константами в данном калькуляторе математические операции производятся над передаточными функциями.
Главная форма калькулятора представлена на рис. 1
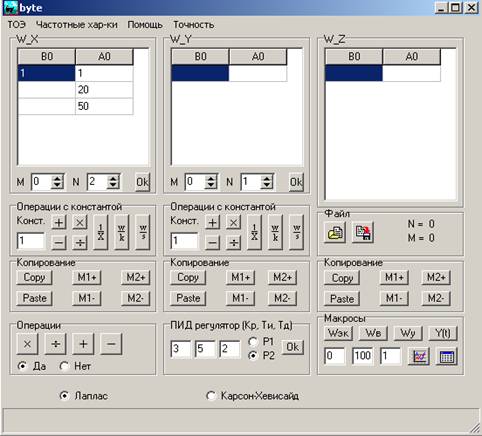
Рис. 1. Главная форма калькулятора
Калькулятор имеет две панели W_X и W_Y в которые вводятся передаточные функции операндов. Результат вычислений выводится на панели W_Z.
Передаточные функции представлены в общем виде:
где m-порядок числителя, а n-порядок знаменателя;
и – коэффициенты числителя и знаменателя соответственно.
Например для функции вида панель ввода будет выглядеть следующим образом (рис 2):
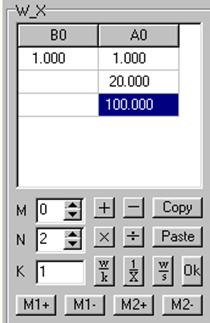
Рис. 2. Пример панели ввода.
В пределах одной передаточной функции в каждой панелей W_X и W_Y можно осуществлять математические операции с константой, введенной в окне К. Можно копировать передаточные функции через промежуточный буфер.
Для расширения промежуточного хранения результатов вычислений реализованы две дополнительные ячейки памяти М1 и М2, в которые можно копировать передаточные функции из любой панели или поместить передаточную функцию из выбранной ячейки в любую панель.
С помощью калькулятора над передаточными функциями можно производить операции вида: сложение, вычитание, умножение и деление.
Особенностью калькулятора является то, что с помощью него можно решать несколько видов электротехнических задач на нахождение тока и напряжения (рис. 3), на статических и динамических звеньях.
Также с помощью этого калькулятора можно вычислить аналитические выражения переходного процесса, корни характеристического уравнения и вывести график этой функции в графическом модуле (рис. 4)
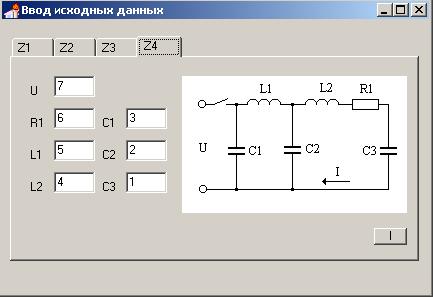
Рис. 3. Решение электротехнических задач.
Рис. 4. Отображение переходного процесса.
В графическом модуле можно просматривать несколько графиков сразу, загружать их из файла и сохранять.
Опыт использования калькулятора в течение 5 лет выявил некоторые его недостатки. Для их исправления были поставлены следующие задачи:
- Исправить ошибки нахождения аналитической функции по передаточной
- Добавить возможности нахождения аналитической функции по передаточной с нулевыми и кратными корнями знаменателя
- Добавить возможности нахождения аналитической функции по передаточной с преобразованием Лапласа.
- Добавить алгоритм нахождения оптимальных настроек П, ПИ, ПД, ИД и ПИД регуляторов.
- Усовершенствовать калькулятор, так чтобы он мог производить операции с передаточными функциями с запаздыванием.
- Связать модули построения графика передаточной функции, нахождения оптимальной передаточной функции по этому графику и данного калькулятора.
- Связать калькулятор с базой данных, в которой будут храниться сами передаточные функции и их графики.
К данному времени выполнены первые три пункта из этого списка.
Для выполнения второго и третьего пункта было удалено старое и внедрено новое [2] преобразование Лапласа вида
где — полюсы , а — их кратности.
На практике очень часто требуется оптимизировать автоматическую систему регулирования, для этого требуется подобрать оптимальный регулятор и определить его оптимальные настройки. Выбор критерия оптимальности является одной из ответственных и сложных задач расчета системы регулирования.
В практике наладки автоматизированных систем регулирования промышленных объектов химической технологии преобладает подход, связанный с минимизацией оценок качества регулирования вдоль границы области допустимых по условиям задачи заданного запаса устойчивости. Для выполнения четвертого пункта требуется найти запас устойчивости параметрической модели объекта регулирования. Для ее решения были найдены методы нахождения запаса устойчивости и оптимальных настроек регуляторов по методу расширенных комплексных частотных характеристик. В ближайшее время по этим методам будут составлены алгоритмы и в дальнейшем внедрены в виде одной из функций калькулятора.
После внесенных изменений, калькулятор передаточных функций позволяет находить оптимальные передаточные функции из эксперимента, далее проводить различные действия с передаточными функциями объектов регулирования, находить оптимальные воздействия, запасы устойчивости, в том числе для объектов с запаздыванием, характерных для предприятий химической технологии Верхнекамья.
- Бильфельд Н.В., Беккер В.Ф. Имитационное моделирование систем цифрового управления.– Пермь: Пермский гос. техн. ун-т, 2002.– 52 с.
- Диткин В.А., Прудников А.П. Интегральное преобразование и операционное исчисление.– М.: Высшая школа, 1961.– 524 с.
Источник: fundamental-research.ru